Prüfungsaufgaben Mathematik 2024
🎓 Prüfungsbereich für Berlin
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Formelsammlung, die bei der Prüfung beiliegt.
- 1
Aufgabe 1: Basisaufgaben
Kreuzen Sie an, wie viele Minuten Stunden sind. (1P)
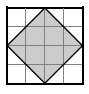
Von einer Figur wurde ein Teil grau eingefärbt.
Geben Sie den Anteil der grau markierten Fläche an. (1P)
Ein gleichseitiges Dreieck hat die Seitenlänge .
Kreuzen Sie die Formel zur Berechnung des Umfangs an. (1P)
Geben Sie die Lösung der Gleichung , an. (1P)
Der Eintrittspreis in ein Schwimmbad beträgt .
Der Preis wird um erhöht.
Geben Sie den neuen Eintrittspreis in Euro an. (1P)
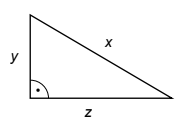
Kreuzen Sie die Gleichung an, mit der die Länge der Dreiecksseite des nebenstehenden Dreiecks berechnet werden kann. (1P)
Geben Sie den Wert für an, so dass gilt: . (1P)
Ermitteln Sie den Median (den Zentralwert) der folgenden Datenreihe: (2P)
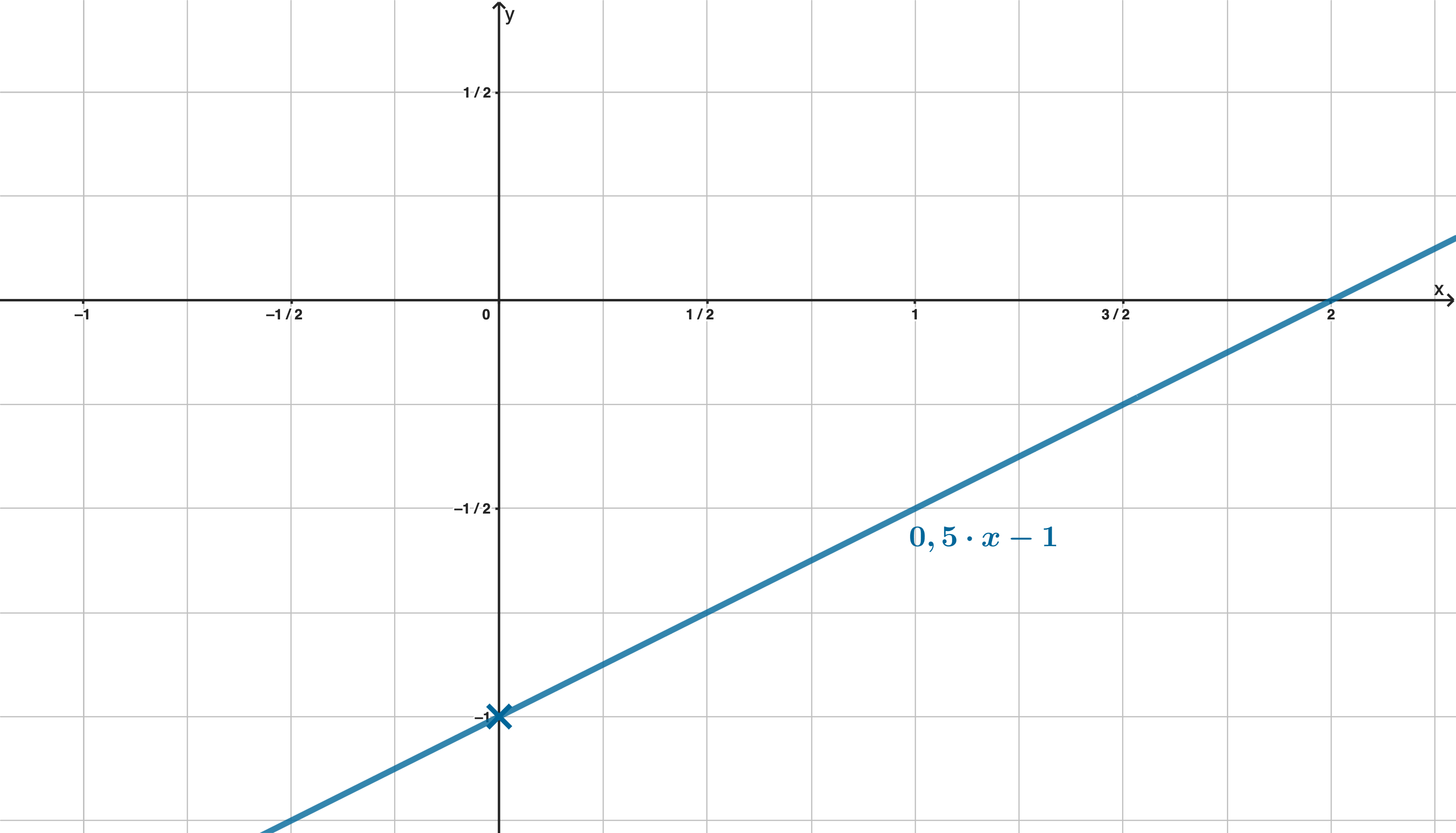
Eine Gerade hat die Gleichung
Markieren Sie im Koordinatensystem den
Schnittpunkt der Geraden mit der -Achse.
(1P)
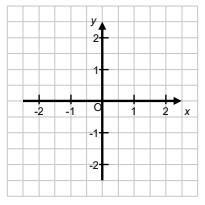
- 2
Aufgabe 2: Niederschläge
Im Diagramm sind die monatlichen Niederschläge des Jahres 2021 in Brandenburg
dargestellt.
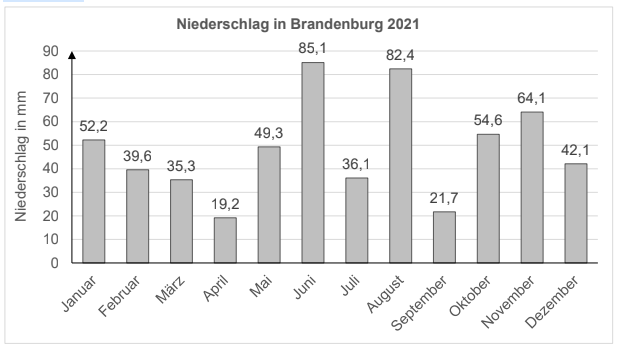
Ermitteln Sie für das Jahr 2021 die Spannweite der monatlichen Niederschläge in mm. (2P)
Im gesamten Jahr 2021 fielen insgesamt 581,7 mm Niederschlag.
Zeigen Sie, dass der Durchschnitt der monatlichen Niederschläge im Jahr 2021 ca. beträgt.
Ermitteln Sie, um wie viel Prozent der Niederschlag des Monats April unterhalb des monatlichen Durchschnitts liegt.
(3P)
Die Familie Schulz verbraucht täglich ca. Liter Leitungswasser.
Die Tabelle zeigt ihren Verbrauch.

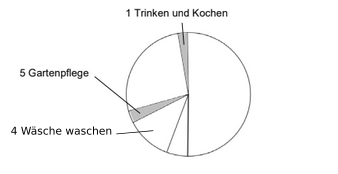
Im Kreisdiagramm sind die Anteile aus der Tabelle dargestellt.
Beschriften Sie den Anteil für „Wäsche waschen“ im Kreisdiagramm.
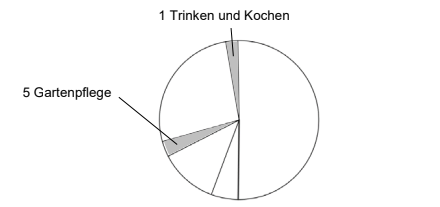
Berechnen Sie die Winkelgröße für den Anteil 1 „Trinken und Kochen“ vom
gesamten Wasserverbrauch.
(3P)
Für die tägliche Gartenpflege soll das Leitungswasser durch Regenwasser
ersetzt werden. Ein Liter Leitungswasser kostet .
Berechnen Sie, wie viel Geld Familie Schulz pro Tag sparen würde. (1P)
- 3
Aufgabe 3: Funktionen
Gegeben ist eine lineare Funktion mit der Gleichung 1.
Ihr Graph ist die Gerade .
Gegeben ist eine quadratische Funktion mit der Gleichung .
Ihr Graph ist die Parabel .
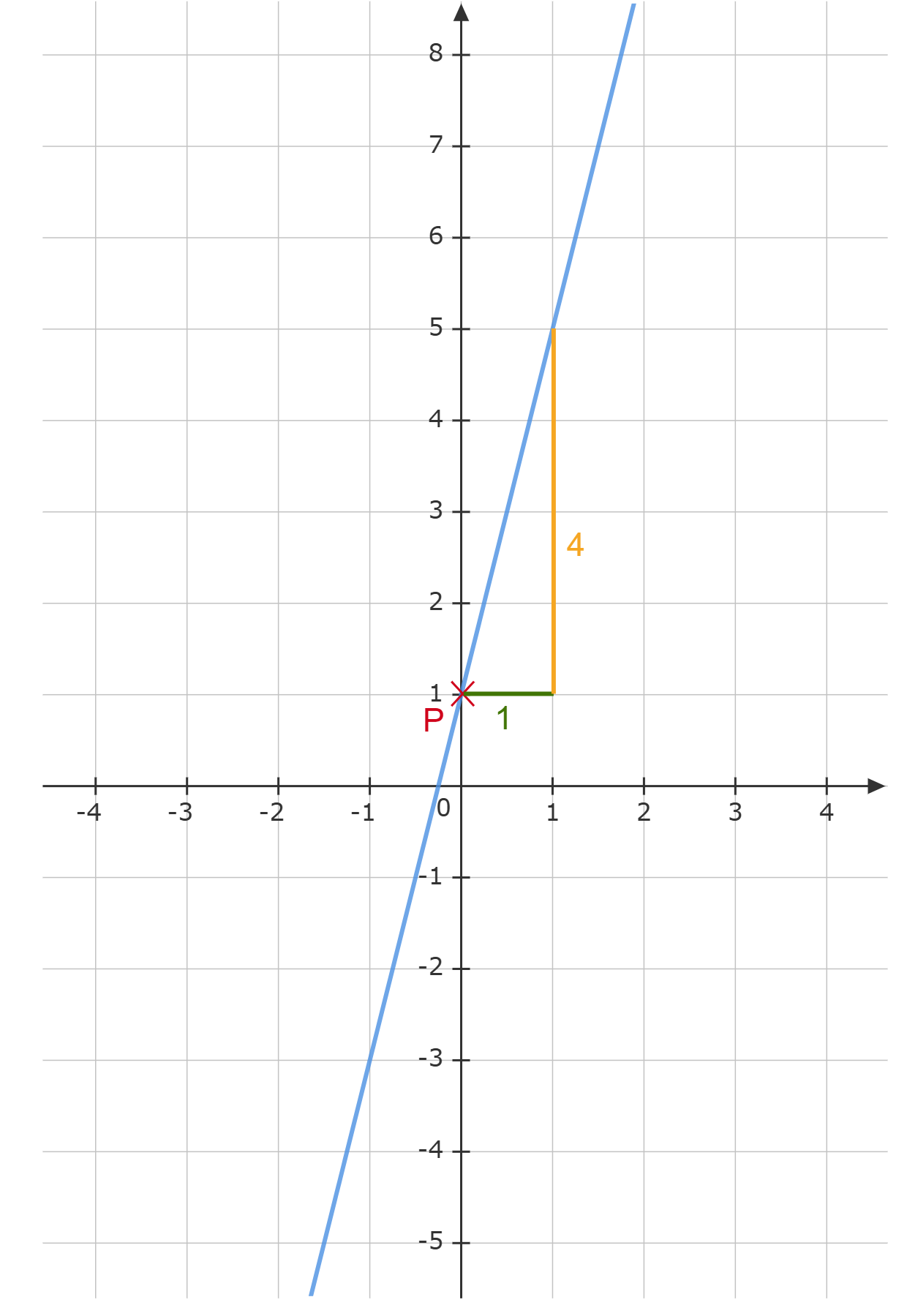
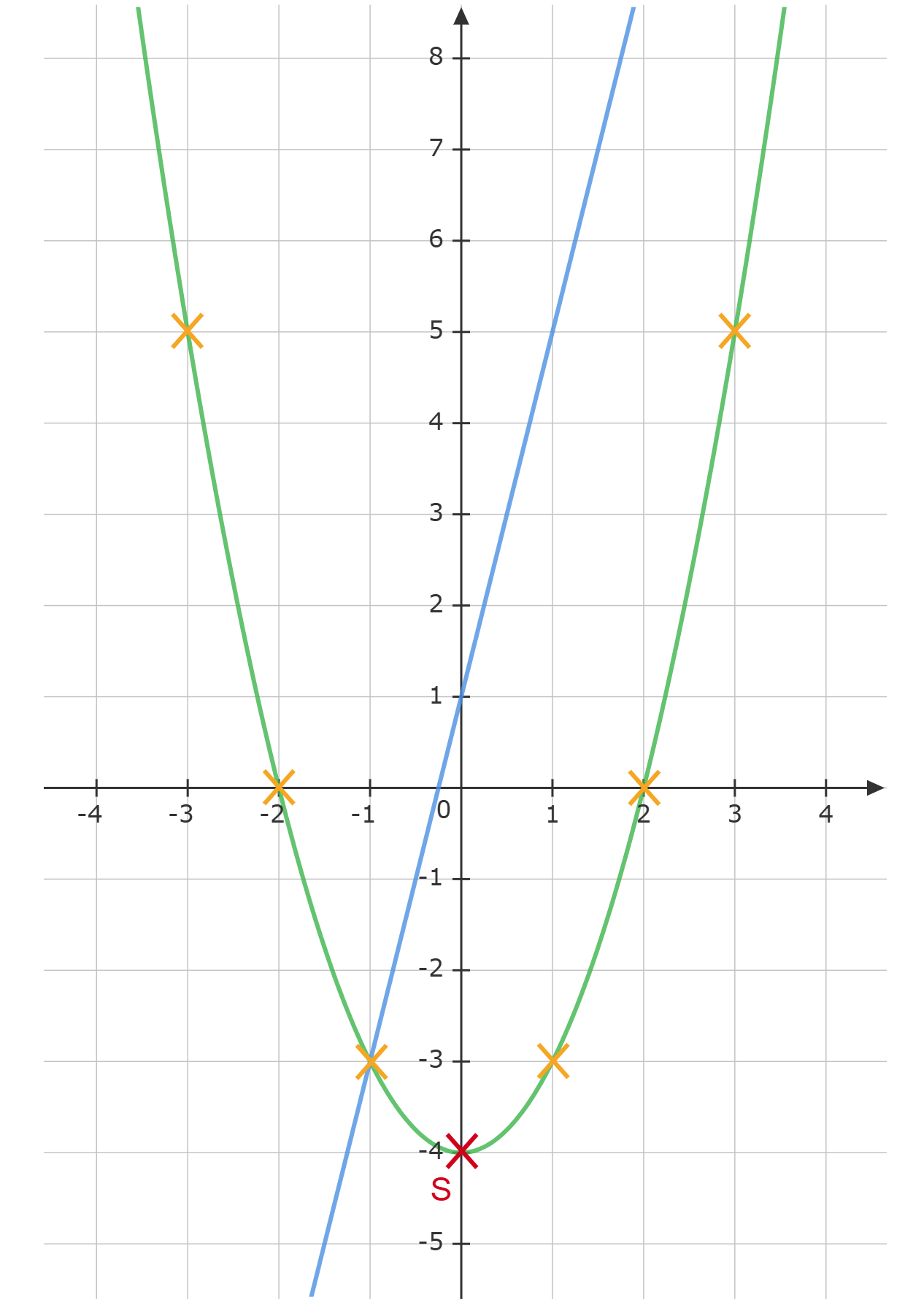
Zeichnen Sie die Gerade in das Koordinatensystem ein. (2P)
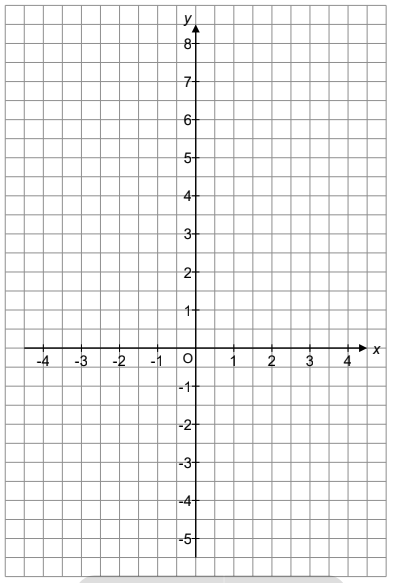
Skizzieren Sie die Parabel in das Koordinatensystem. (2 P)
Geben Sie die Koordinaten des Scheitelpunktes der Parabel an.
Überprüfen Sie rechnerisch, ob der Punkt auf der Parabel liegt. (2P)
Die Graphen von und schneiden sich in zwei Punkten.
Berechnen Sie die Koordinaten der Schnittpunkte der Geraden mit der Parabel .
(4P)
- 4
Aufgabe 4: Kegel
Eine Firma stellt Kegel her.
Berechnen Sie den Flächeninhalt der Grundfläche des Kegels. (2P)
Für den Transport soll der Kegel in einen quaderförmigen Karton verpackt werden.
Die Verpackung soll so klein wie möglich sein, aber so groß, dass der Kegel
vollständig hineinpasst.
Skizzieren Sie den Kegel in die Verpackung. (4P)
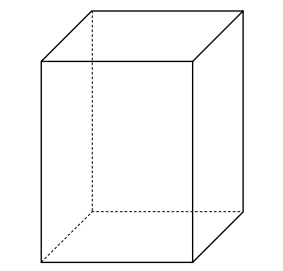
Es stehen vier Verpackungen zur Auswahl.
Wählen Sie die kleinstmögliche Verpackung (Länge x Breite x Höhe) für den
Kegel aus. Kreuzen Sie an.
Begründen Sie ihre Entscheidung.
Eine andere Firma verschickt den gleichen Kegel in einer zylinderförmigen
Verpackung mit folgenden Innenmaßen: , .
Um den Kegel beim Transport zu schützen, soll das Restvolumen der
zylinderförmigen Verpackung mit Füllmaterial aufgefüllt werden.
Ermitteln Sie, wie viele Füllmaterial benötigt werden. (3P)
- 5
Aufgabe 5: Hausarbeit
Bei Familie Siebert muss jedes der 5 Kinder im Haushalt mithelfen.
Die zu erledigenden Aufgaben stehen auf jeweils einem Zettel.
Am Wochenanfang zieht jedes Kind zufällig genau einen Zettel.
Die Aufgaben sind:

Wer den Joker zieht, hat in der Woche frei.
Geben Sie die Wahrscheinlichkeit dafür an, dass das erste Kind „Staubsaugen“
zieht. (1P)
Benjamin ist das jüngste Kind und zieht in jeder Woche als Erster.
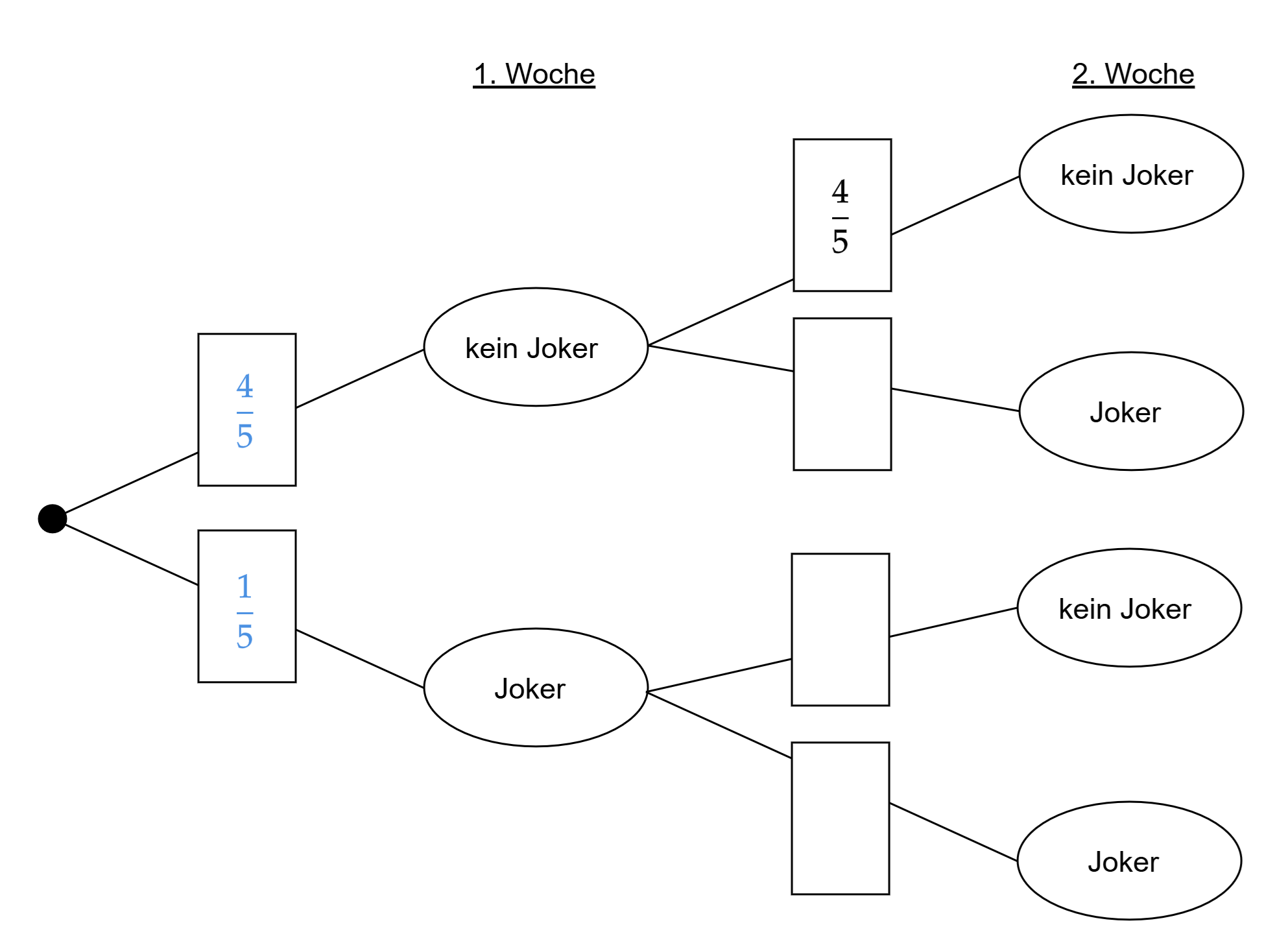
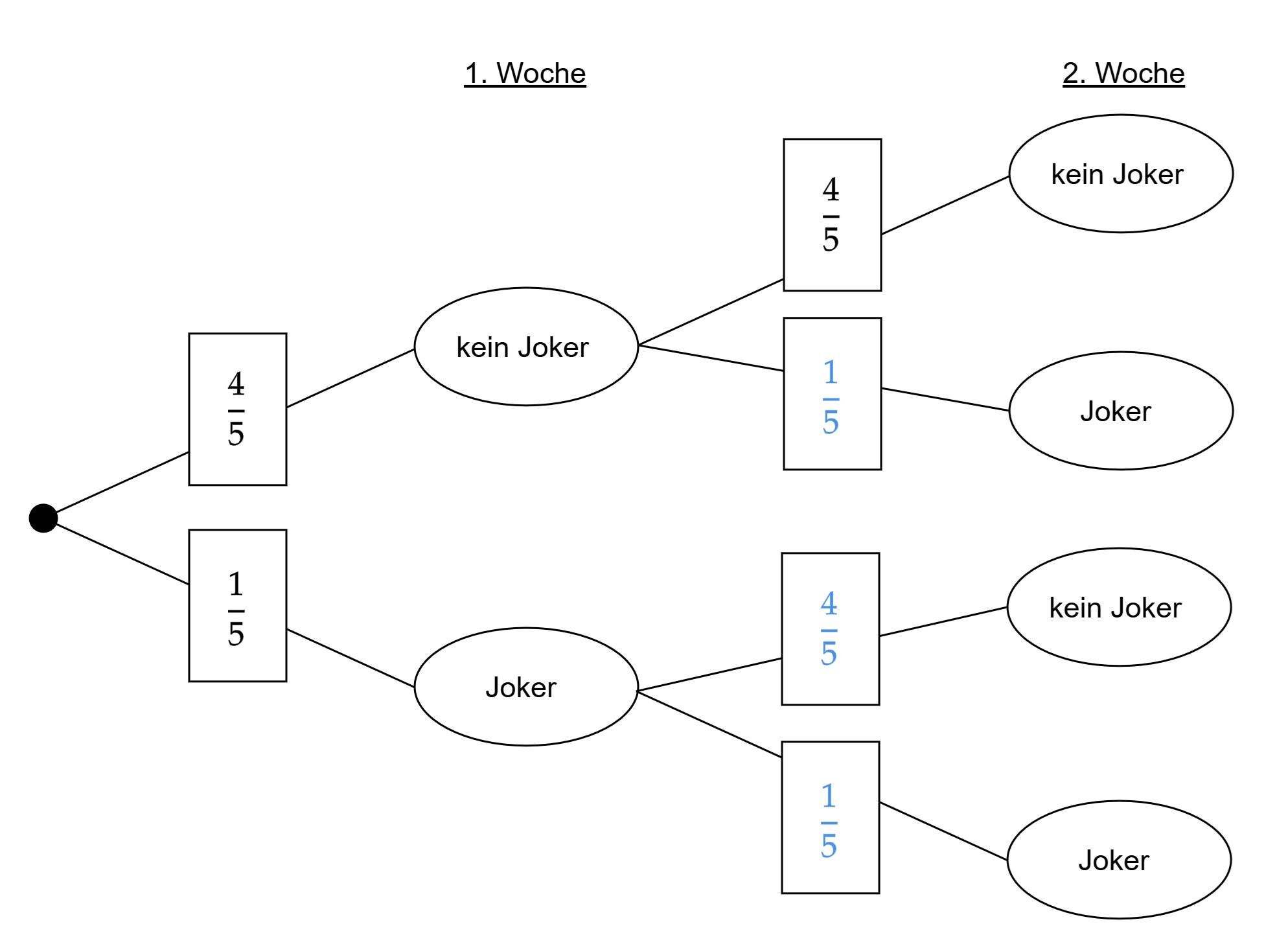
Ergänzen Sie die Wahrscheinlichkeiten im Baumdiagramm. (3P)
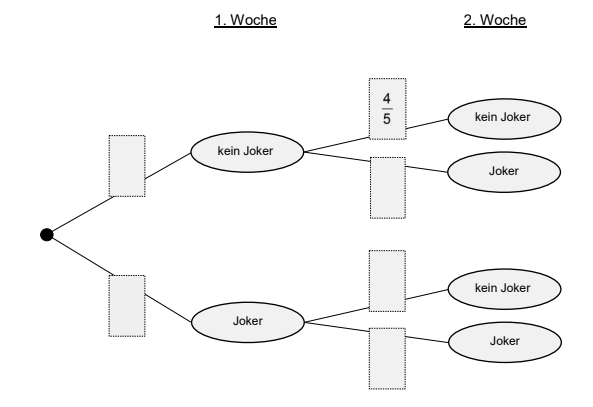
Benjamin zieht in beiden Wochen den Joker.
Weisen Sie nach, dass die Wahrscheinlichkeit dafür beträgt.
Klara zieht immer als zweites Kind nach Benjamin.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass Klara in der ersten Woche den
Joker zieht. (2P)
- 6
Aufgabe 6: Seilbahn
Eine Seilbahn verbindet die beiden Orte und .
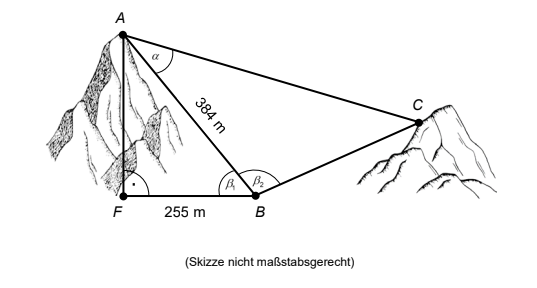
Die Strecke kennzeichnet den Höhenunterschied zwischen den Orten und .
Berechnen Sie diesen Höhenunterschied. (2P)
Bestimmen Sie die Größe des Winkels , mit der die Seilbahn von nach
fährt. (2P)
Die Seilbahn fährt von nach mit einer durchschnittlichen Geschwindigkeit
von 3.
Ermitteln Sie die Dauer für eine Fahrt mit der Seilbahn.
Geben Sie das Ergebnis in Minuten an. (2P)
Der Ort und der Ort sind mit einer weiteren Seilbahn verbunden.
Folgende Angaben sind bekannt:
und .
Berechnen Sie die Länge der Seilbahnstrecke von nach . (4P)
- 7
Aufgabe 7: Blumenstrauß
Die Geschwister Daniel und Filip wollen ihrer Mutter jeweils einen Blumenstrauß zum Muttertag kaufen.
Daniel kauft seinen Blumenstrauß in Geschäft A.
Filip kauft seinen Blumenstrauß in Geschäft B.

Im Geschäft kosten eine Rose und eine Tulpe zusammen €.
Für Rosen und Tulpen zahlt Daniel insgesamt €.
Stellen Sie ein lineares Gleichungssystem zu diesem Sachverhalt auf.
Dabei gilt: : Preis pro Rose: Preis pro Tulpe. (2P)
Im Geschäft ist der Preis für eine Rose € und der Preis für
eine Tulpe €.
Filip stellt zu seinem Blumenstrauß folgendes Gleichungssystem auf.
Formulieren Sie einen Satz, der den Sachverhalt beschreibt, der durch
Gleichung II ausgedrückt wird.
Ermitteln Sie die Lösung für das Gleichungssystem. (4P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?