Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Vereinfachen Sie den Term so weit wie möglich. (2 BE)
- 2
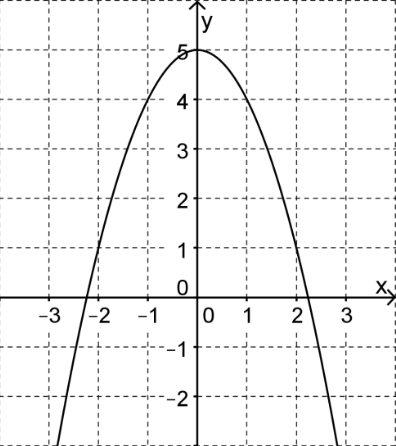
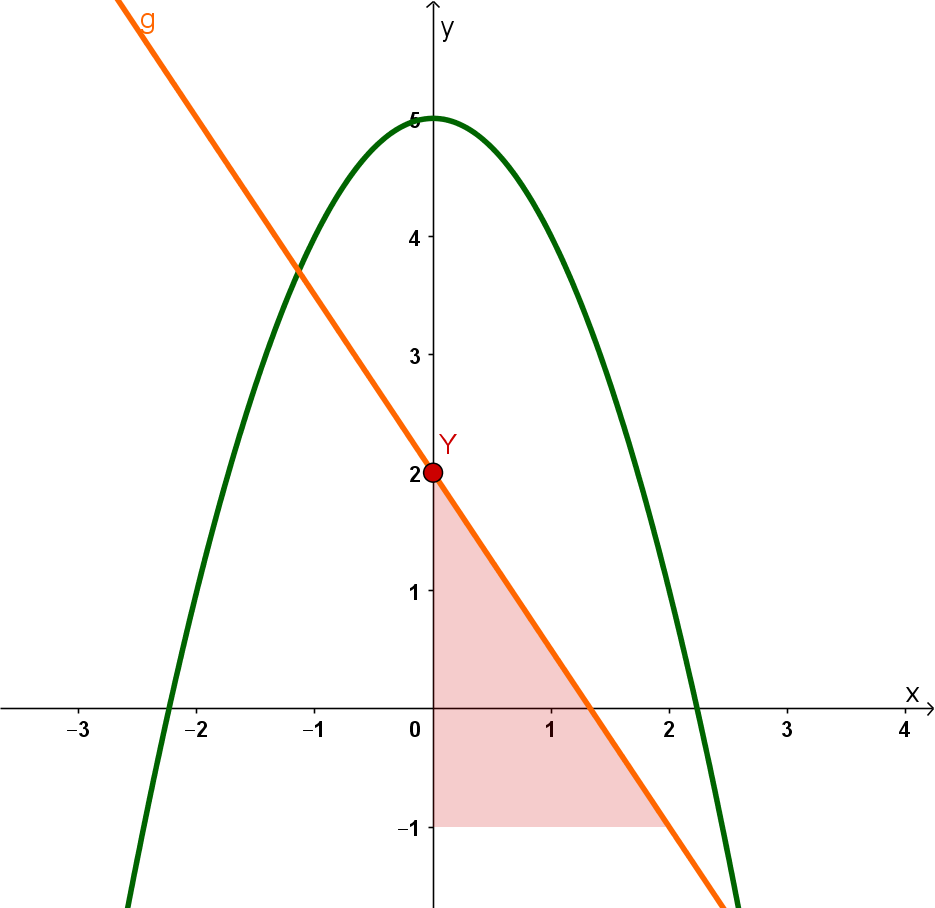
Die Abbildung zeigt eine zur Normalparabel kongruente Parabel mit der Gleichung y=f(x).
Geben Sie einen passenden Term f(x) an. (1 BE)
Zeichnen Sie die Gerade g mit der Gleichung y=2- x in die Abbildung ein. (1 BE)
Beschreiben Sie, wie man rechnerisch die Koordinatender Punkte ermitteln kann, in denen sich die Parabelund die Gerade schneiden. (2 BE)
- 3
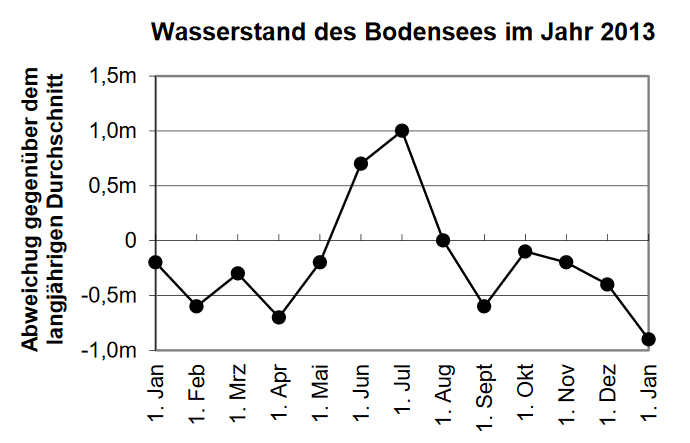
Der im Folgenden als konstant angenommene Flächeninhalt der Wasserfläche des Bodensees beträgt ungefähr 500 Millionen m². Im langjährigen Durchschnitt enthält der See 50 Milliarden m³Wasser. Das nebenstehende Diagramm zeigt vereinfacht für das Jahr 2013 die Abweichungen des Wasserstands des Sees gegenüber dem langjährigen Durchschnitt.
Kreuzen Sie an, in welchem Monat der Wasserstand des Bodensees im Jahr 2013 lautDiagramm am stärksten angestiegen ist. (1 BE)
Berechnen Sie, um wie viel Prozent der Wasserinhalt des Sees am 1. Juli 2013 größer als der langjährige Durchschnittswert war. (2 BE)
Geben Sie den Flächeninhalt der Wasserfläche des Bodensees in km² an. (1 BE)
Auf einer Informationstafel steht, dass auf der Wasserfläche des Bodensees 2 Milliarden Menschen Platz fänden. Machen Sie diese Aussage plausibel. (1 BE)
- 4
Ein mit den Ziffernvon 1 bis 6 beschrifteter Laplace-Würfel wird dreimal nacheinandergeworfen. Geben Sie dazu in Worten ein Ereignis an, das die Wahrscheinlichkeit ()³ hat. (1 BE)
- 5
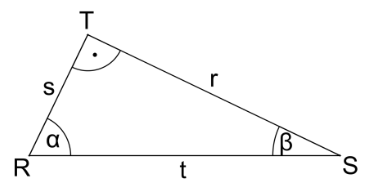
Die Abbildung zeigt ein rechtwinkliges Dreieck mit den Seiten r, s und t sowie den Innenwinkeln und .Kreuzen Sie jeweils nur die zutreffenden Aussagen an.
Welche Aussage(n) ist (sind) richtig?
Welche Aussage(n) ist (sind) richtig?
- 6

Die Abbildung zeigt eines der ersten Windräder Bayerns, das im Jahr 1995 in Schnaitsee (Oberbayern) errichtet wurde.
Schätzen Sie mithilfe der Abbildung Radius und Inhalt der vom Rotor überstrichenen Kreisfläche ab. (2 BE)
Hinweis: Bei einer Abschätzung muss grundsätzlich der Lösungsweg nachvollziehbar sein.
Für die von einem Windrad erzeugte elektrische Leistung P gilt P=c A v³. Dabei ist v die Windgeschwindigkeit, A der Inhalt der vom Rotor überstrichenen Kreisfläche und c eine vom speziellen Windrad abhängige Konstante.
Entscheiden Sie anhand der Formel: Wenn sich die Windgeschwindigkeit verdoppelt, so
Lösen Sie die Formel P=c A v³nach v auf. (1 BE)
- 7
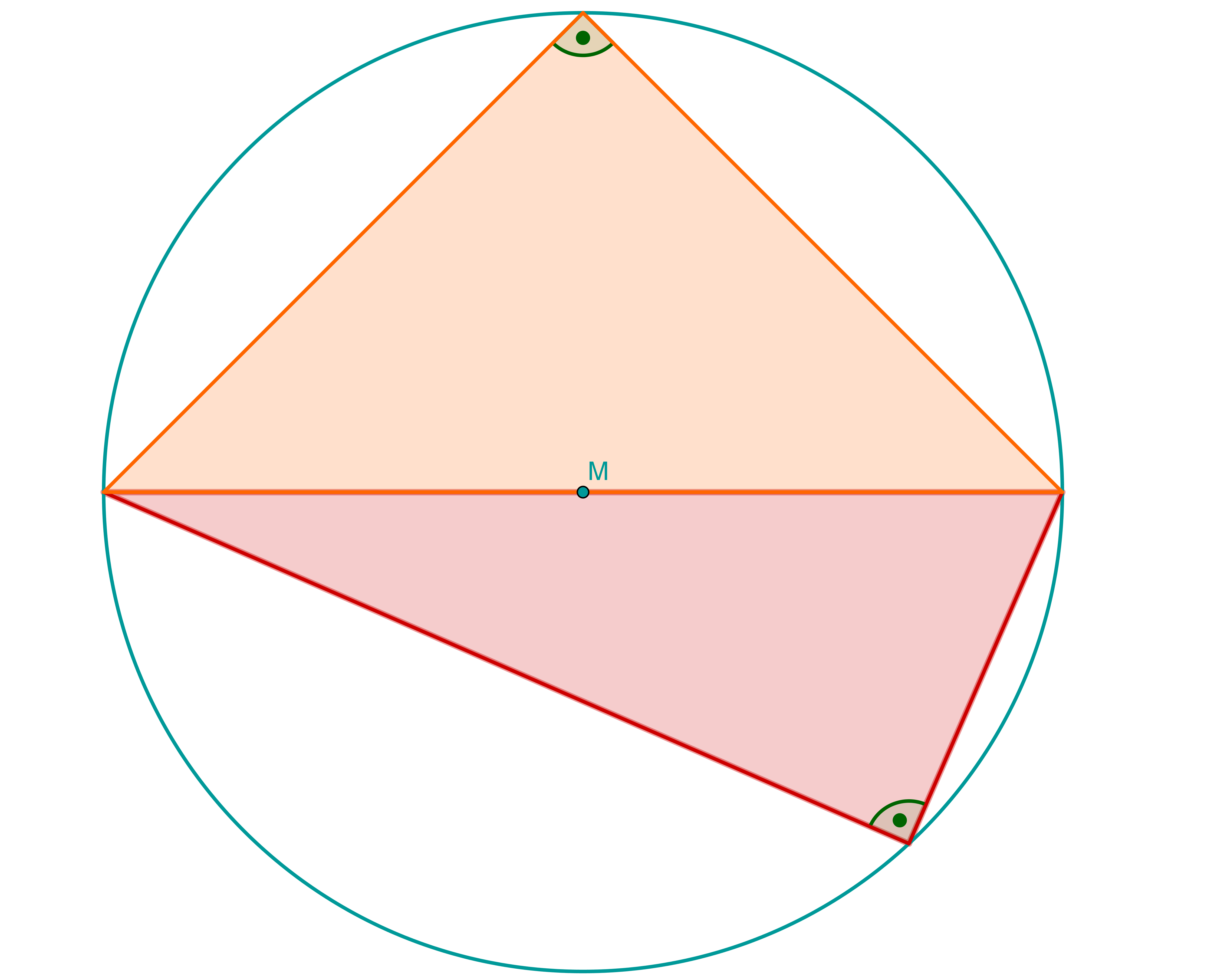
Bekanntlich besitzt jedes Dreieck einen Umkreis, d. h. einen Kreis, auf dem alle Eckpunkte des Dreiecks liegen.
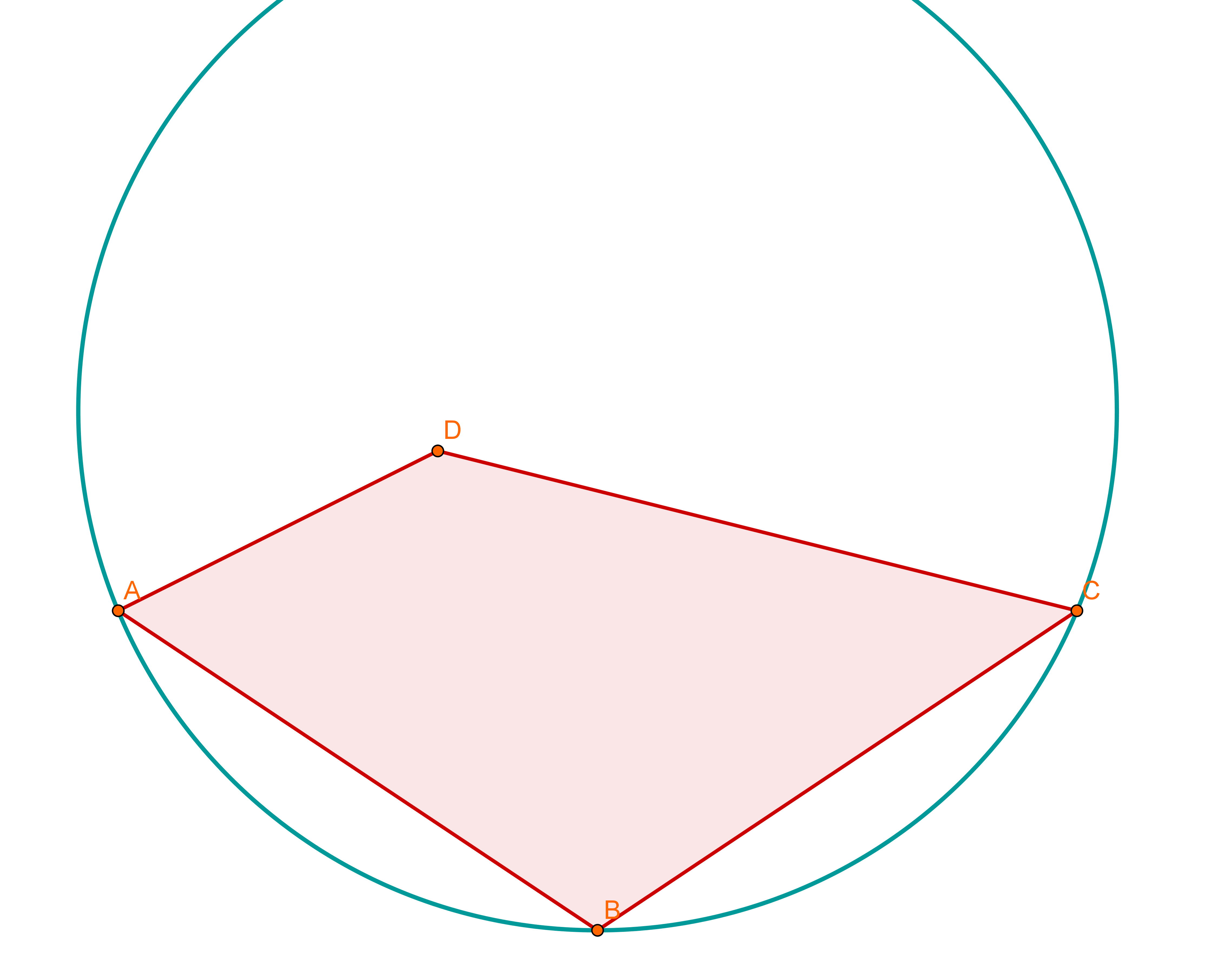
Zeichnen Sie ein Viereck, das offensichtlich keinen Umkreis besitzt. (1 BE)
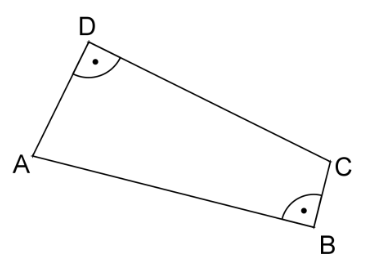
Begründen Sie: Jedes Viereck mit zwei gegenüberliegenden rechten Winkeln besitzt einen Umkreis. (2 BE)
Hinweis: In der Begründung können die Bezeichnungen der abgebildeten Überlegungsfigur verwendet werden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?