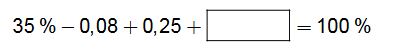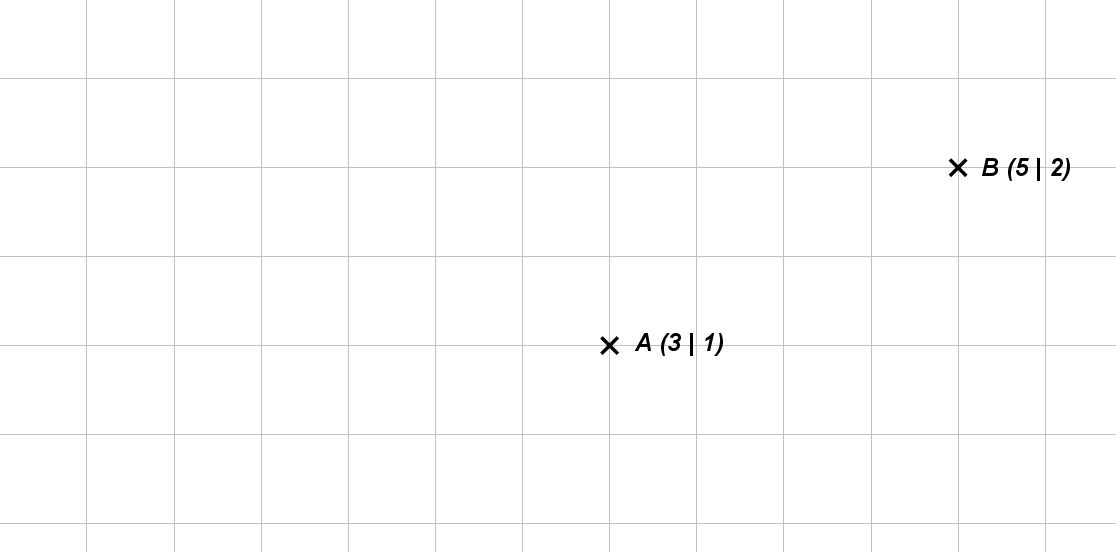Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
In der Klasse 9a sind 24 Jugendliche. Am Dienstag waren 25 % nicht da.Gib an, wie viele Jugendliche anwesend waren. (1 Punkt)
Jugendliche - 2
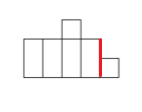
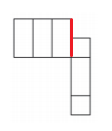
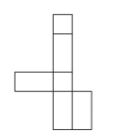
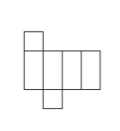
Welche Netze können zu einem Quader gefaltet werden? Wähle alle richtigen Lösungen aus. (1 Punkt)
- 3
Was muss im Platzhalter stehen, dass die Gleichung stimmt. Du kannst dein Ergebnis auch in unser Eingabefeld eingeben um zu prüfen, ob du richtig gerechnet hast. (1 Punkt)
% - 4
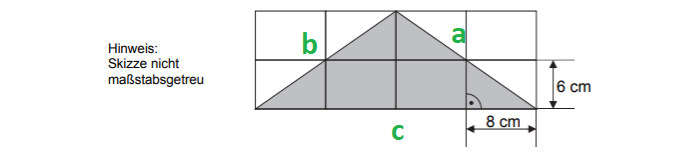
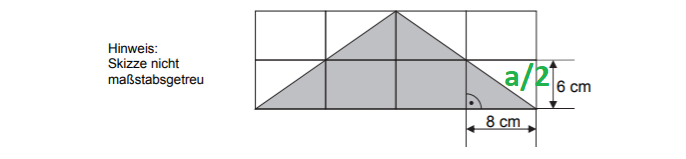
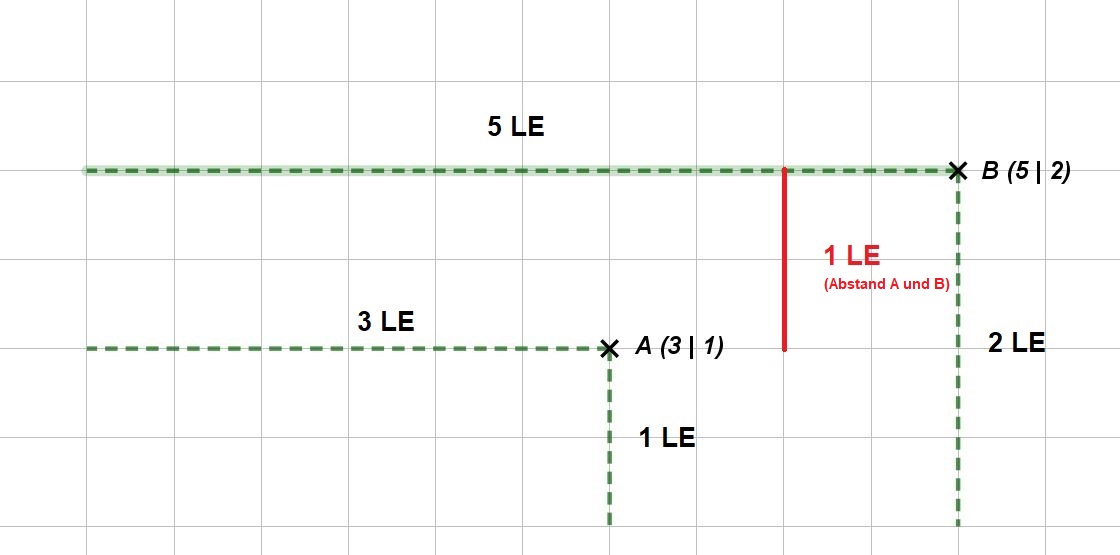
Das Gitter besteht aus acht gleichen Rechtecken.Berechne den Umfang der grau gefärbten Fläche. (2 Punkte)
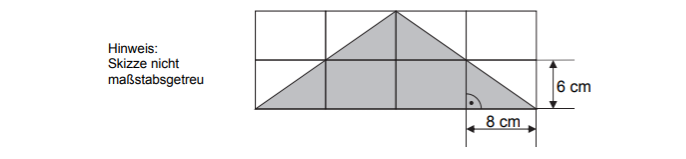 cm
cm - 5
Martina hat zwei Meerschweinchen. Eine Packung Futter reicht für 30 Tage und kostet 4,95 €. (2 Punkte)
Berechne, wie lange eine Packung für drei Meerschweinchen ausreicht.
Gib an, wie viel sie für 6 Packungen bezahlen muss.
- 6
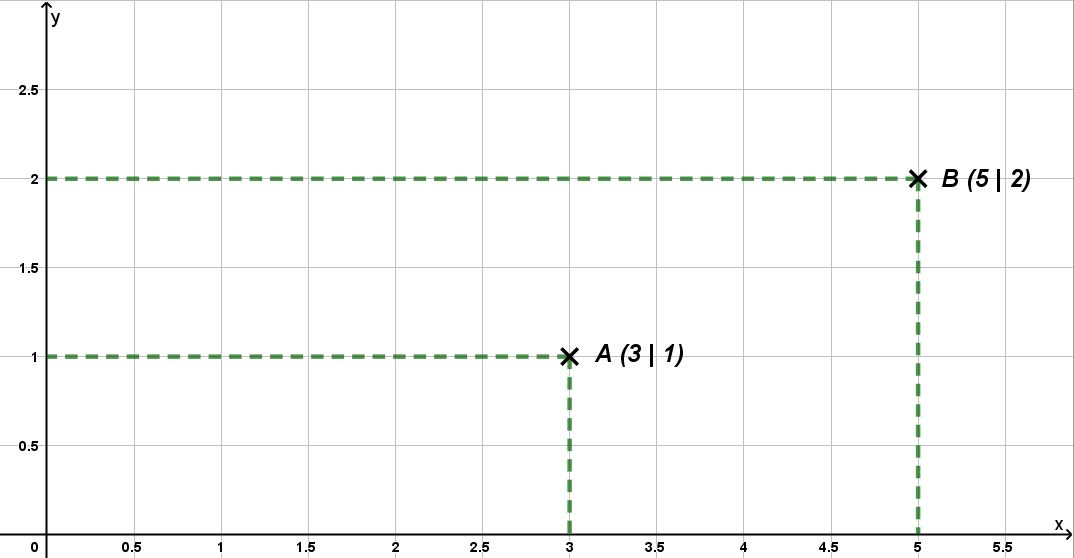
Zeichne das Koordinatensystem so ein, dass die Punkte A und B korrekt eingetragen sind. (1 Punkt)
- 7
Berichtige nur die Zeile, in der ein Fehler gemacht wurde. (1 Punkt)
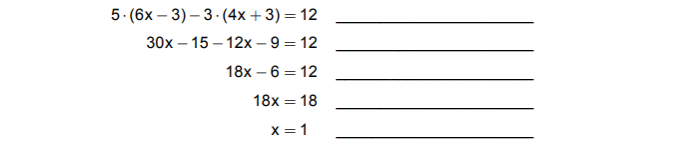
- 8
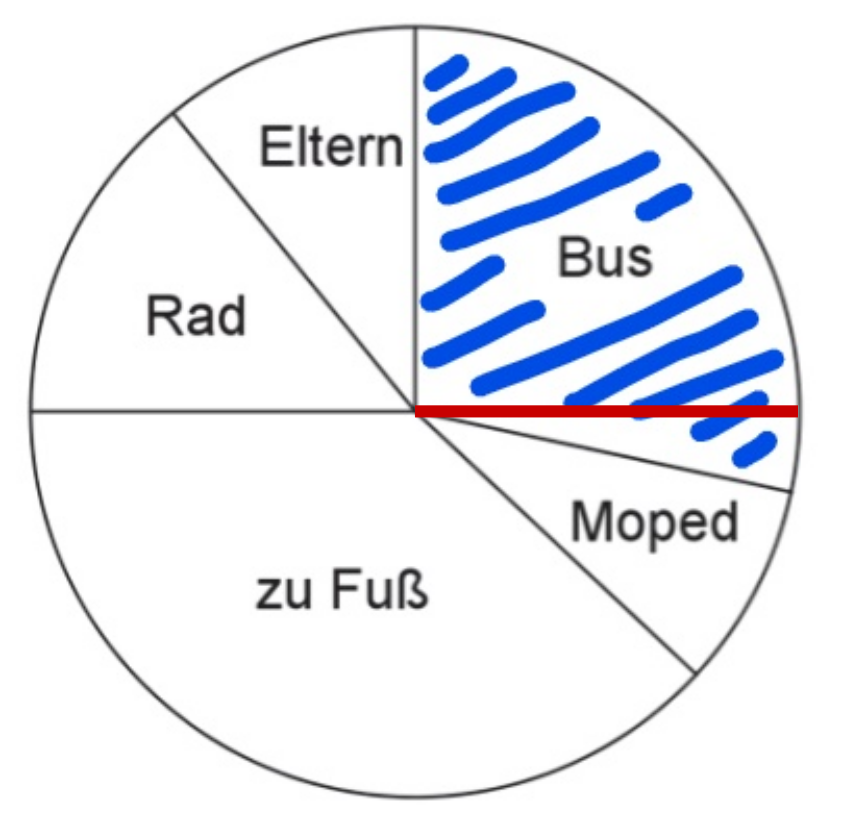
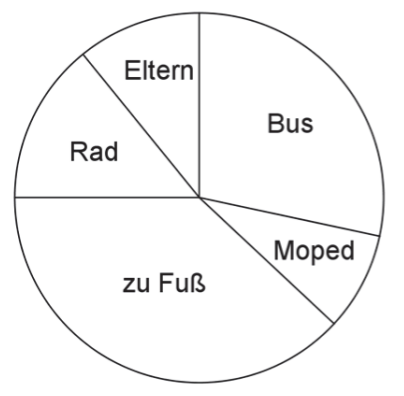
Das Kreisdiagramm zeigt, wie Jugendliche zu ihrer Mittelschule kommen.
Welche Aussage kann nicht stimmen? Wähle aus und begründe deine Entscheidung anhand des Kreisdiagramms. (1 Punkt)
- 9
Was kommt in den Platzhalter? (> oder < oder =)
Gib dein Ergebnis auch in das Eingabefeld ein, um zu prüfen, ob du richtig liegst. (2 Punkte)
- 10
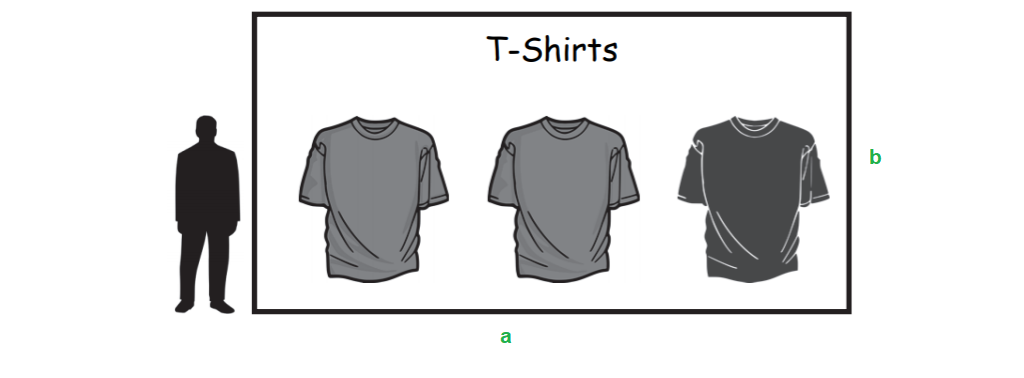
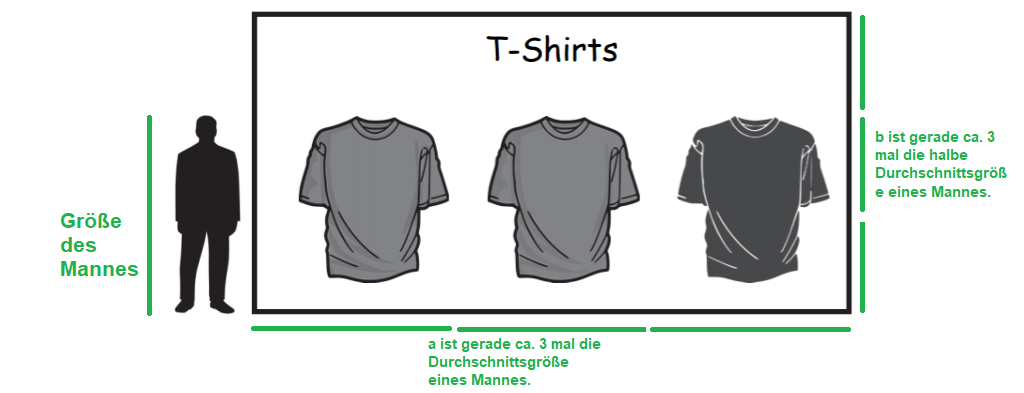
Ein Mann steht neben einer Werbetafel (siehe Abbildung).Schätze den Flächeninhalt der Werbetafel in ab und begründe dein Vorgehen. (2 Punkte)
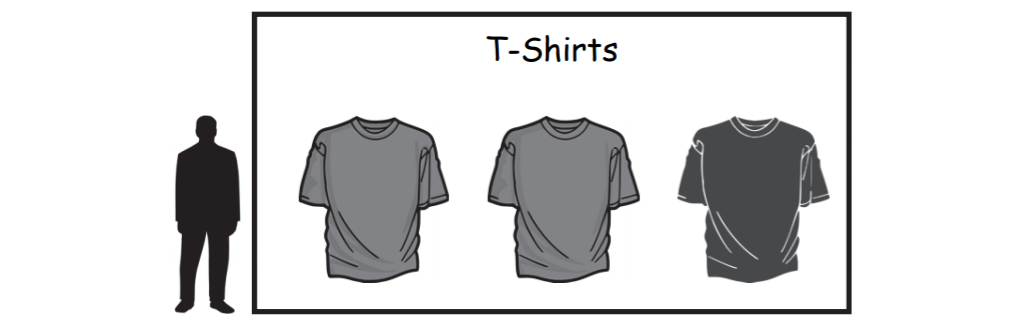
- 11
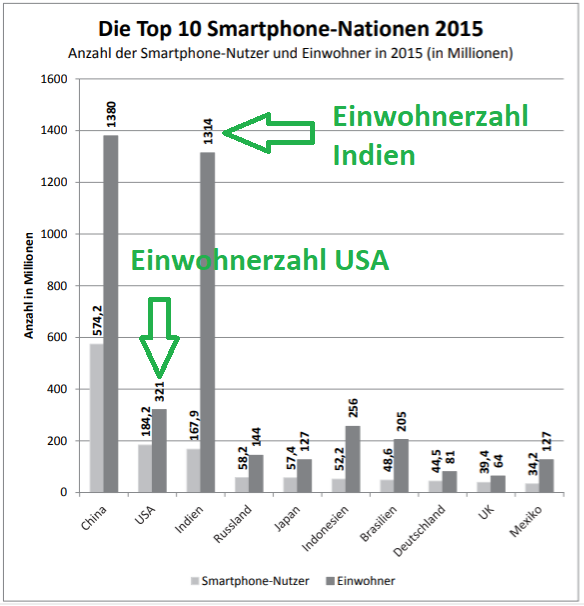
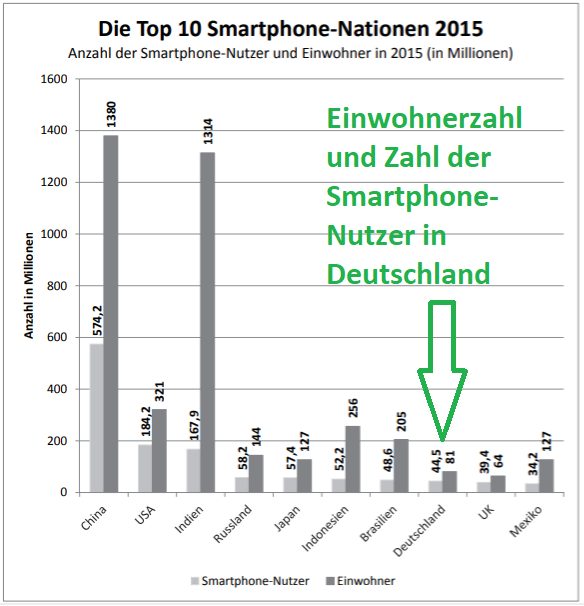
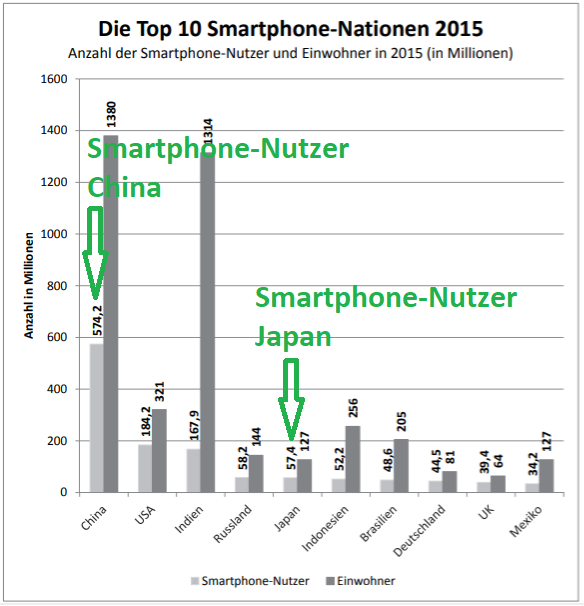
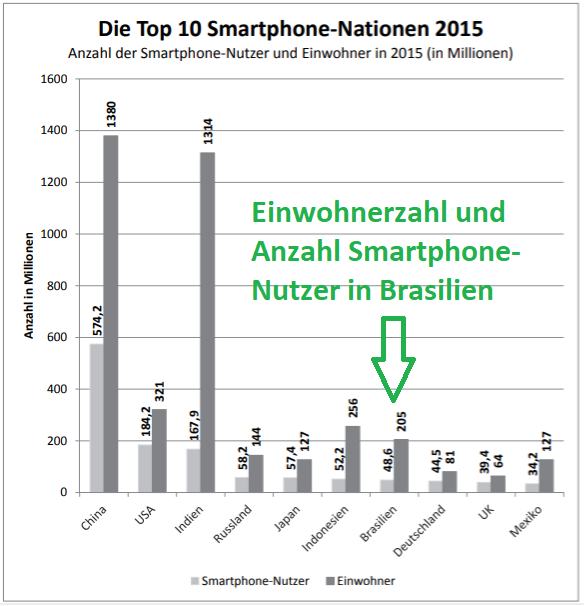
Die Grafik zeigt die Anzahl der Smartphone-Nutzer und die Bevölkerungszahl ausgewählter Länder im Jahr 2015.
Wähle die richtige(n) Antwort(en) aus! (2 Punkte)
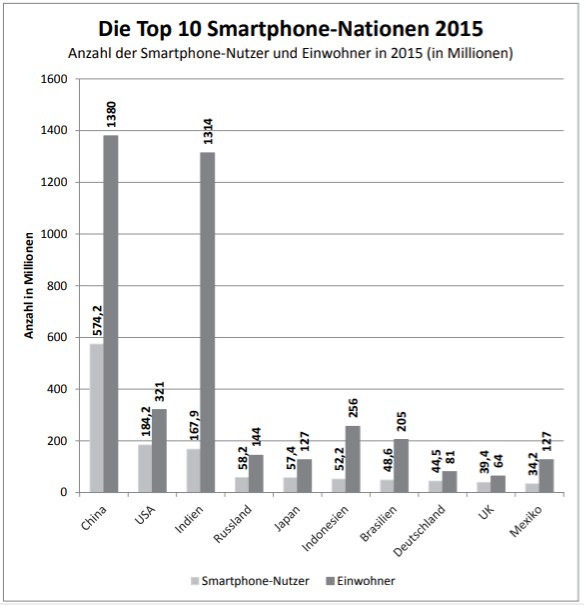
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?