Aufgaben zu Fasskreisbogen und Satz des Thales
Teste dein Wissen zu Fasskreisbogen und Satz des Thales und übe, damit zu rechnen.
- 1
Blickwinkel
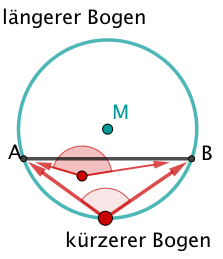
Eine Sehne zerlege einen Kreis in zwei unterschiedlich lange Bogen.
Klicke an was stimmt!
Klicke an was stimmt!
Klicke an was stimmt!
- 2
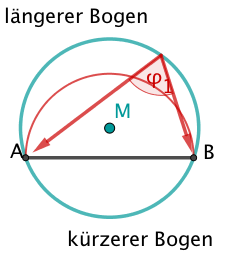
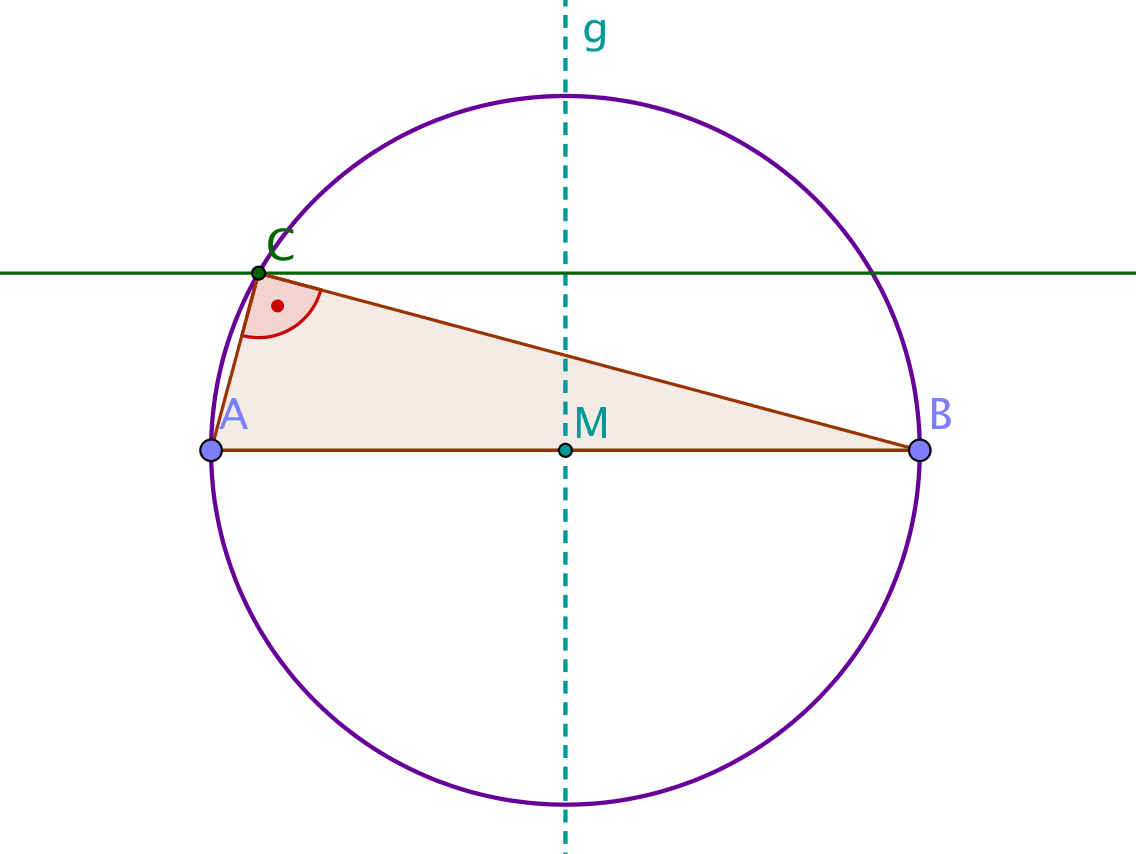
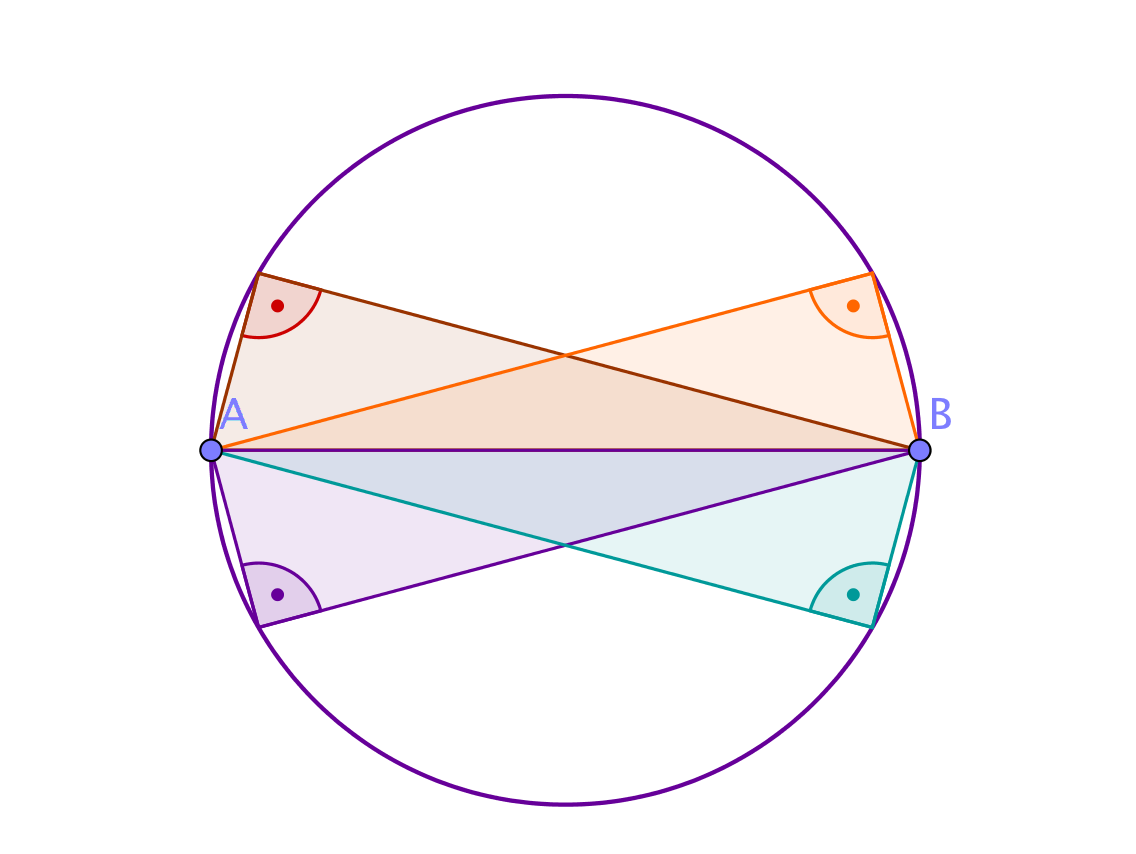
Randwinkel und zugehörige Mittelpunktswinkel
Der Randwinkelsatz (Umfangswinkelsatz; Peripheriewinkelsatz) besagt, dass ein Randwinkel gerade halb so groß ist, wie der zugehörige Mittelpunktswinkel.
Klicke an was stimmt!
Klicke an was stimmt!
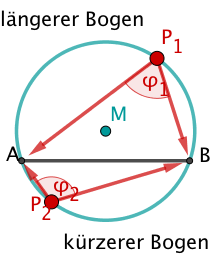
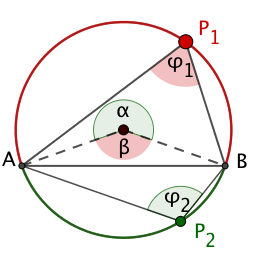
Die beiden Randwinkel auf verschiedenen Seiten einer Sehne ergänzen sich zu 180°.
Zeige, dass hier also gilt:
- 3
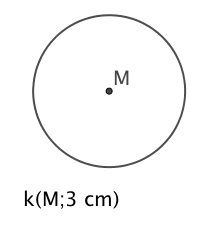
Konstruiere in einem Kreis mit Radius zwei Sehnen, zu denen das Randwinkelpaar 60° und 120° gehört.
- 4
Ein Randwinkel ist um 40° kleiner als der zugehörige Mittelpunktswinkel .
Wie groß sind und ?
- 5
Ein Randwinkel und sein zugehöriger Mittelpunktswinkel betragen zusammen 210°.
Wie groß sind und ?
- 6
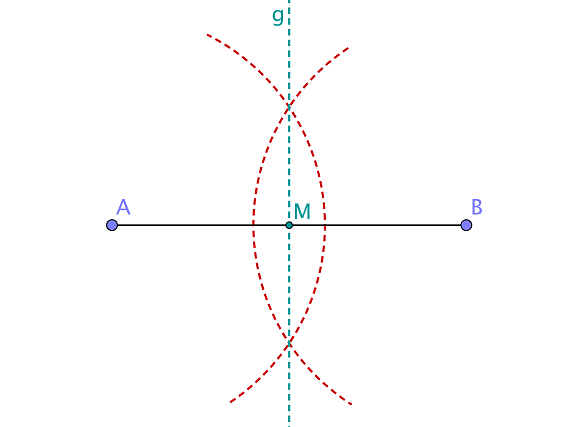
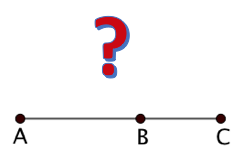
Die Punkte liegen auf einer Geraden (siehe Zeichnung).
Wie viele Punkte in der Zeichenebene gibt es, von denen aus die Strecke unter einem Winkel von 50° und gleichzeitig die Strecke unter dem Winkel 30° erscheint?
Klicke an, was stimmt!
- 7
Konstruiere den Bereich der Zeichenebene, von dem aus eine gegebene Strecke unter einem Winkel mit erscheint.
- 8
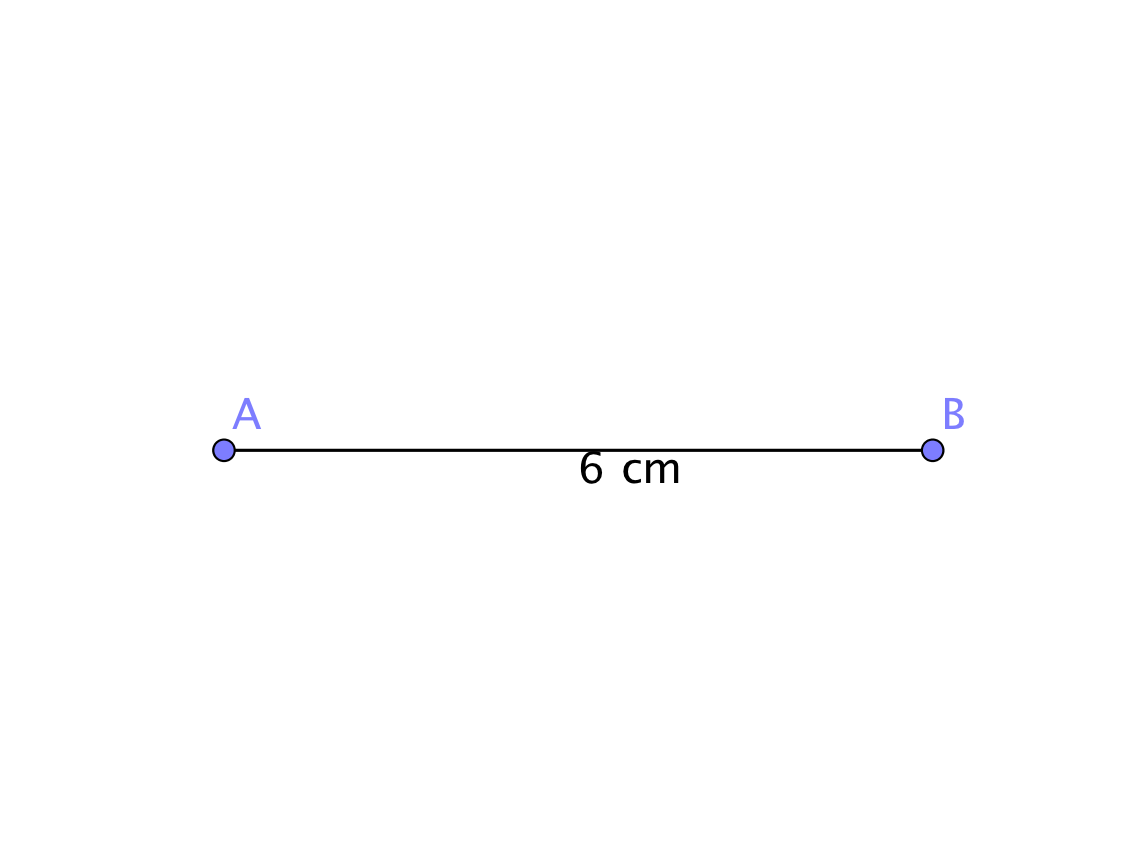
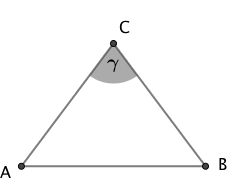
Gegeben ist ein gleichschenkliges Dreieck mit der Basislänge und der Schenkellänge .
Konstruiere unter Beibehaltung der Basis ein gleichschenkliges Dreieck, dessen Winkel an der Spitze
a) halb so groß ist,
b) doppelt so groß ist,
wie der Winkel im Dreieck .
Hinweis:
Die Konstruktion soll ohne Winkelmessungen oder Winkelkonstruktionen erfolgen.
- 9
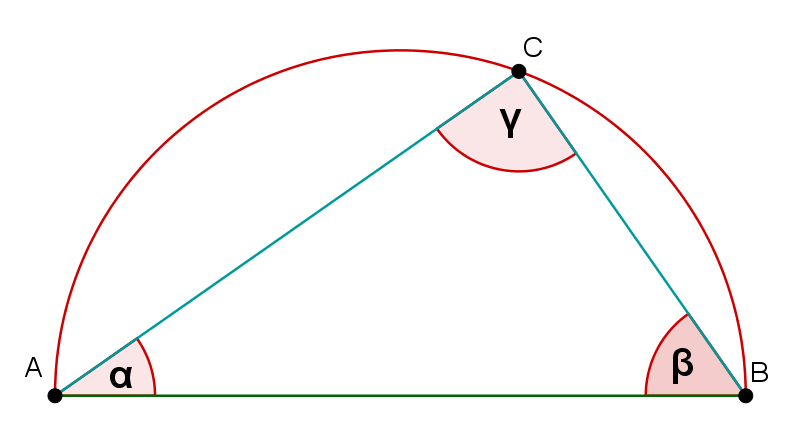
Berechne für die nebenstehende Figur den Winkel , wenn .
Die Punkte liegen auf dem Halbkreis.
° - 10
Die Punkte liegen auf dem Halbkreis.
Gegeben sind weiter die Winkel und .
Berechne die Winkel und .
- 11
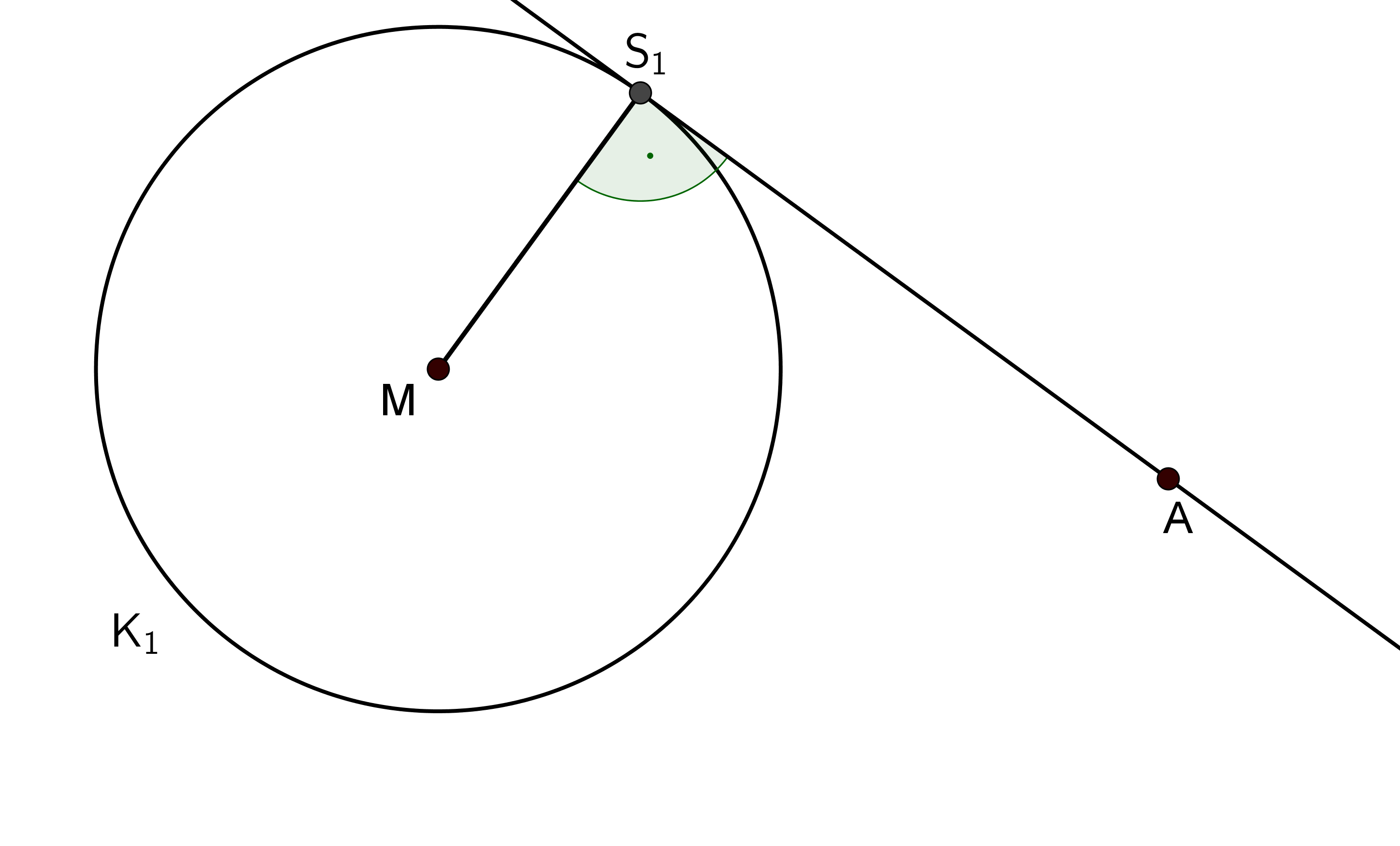
Gegeben ist - wie in nebenstehender Abbildung dargestellt - der Kreis mit Mittelpunkt und ein Punkt , der außerhalb des Kreises liegt.
Konstruiere eine Tangente des Kreises durch den Punkt .

- 12
Konstruiere ein rechtwinkliges Dreieck mit der Hypotenusenlänge und der zugehörigen Höhe . Gibt es mehrere Lösungen?
- 13
Beweiskunst
Der Punkt P liege auf dem Fasskreis der Sehne so, dass die Strecke Durchmesser ist.
Beweise für diese Lage von P den Randwinkelsatz, indem du zeigst, dass gilt:
.
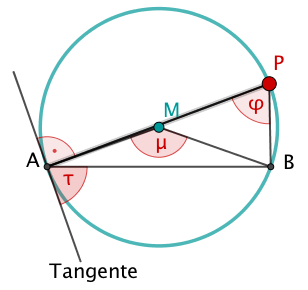
- 14
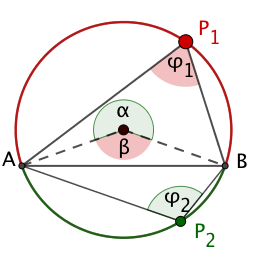
Der Randwinkelsatz (Umfangswinkelsatz; Peripheriewinkelsatz) - Beweis
Zeige:
Für jeden von und verschiedenen Punkt auf dem Fasskreis der Sehne gilt:
Der Randwinkel bei ist halb so groß wie der zugehörige Mittelpunktswinkel .
Der Randwinkel bei ist gleich dem Sehnen-Tangentenwinkel .
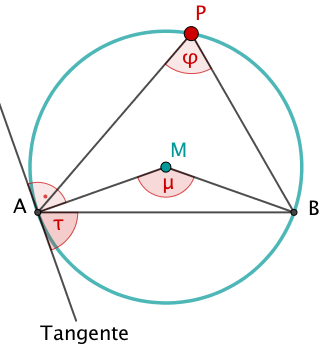
- 15
Konstruiere mithilfe des Thaleskreises die Winkel und . Du darfst nur Zirkel und Lineal (kein Geodreieck) verwenden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?