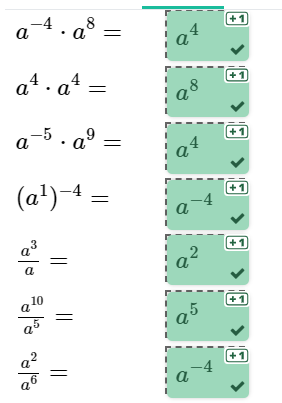Aufgaben zu den Potenzgesetzen
Lerne mit diesen Übungsaufgaben, Potenzen auszurechnen und die verschiedenen Potenzgesetze anzuwenden.
- 1
Rechne mit den Potenzgesetzen
Ordne den Termen den richtigen Wert zu.
Verwende die Potenzgesetze, um die Terme zusammenzufassen.
- 2
Wende die Potenzgesetze an, um folgende Ausdrücke zu vereinfachen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Wende das Potenzgesetz an. Hier ist .
↓ Fasse den Exponent zusammen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Wende zunächst die Potenzgesetze auf an.
↓ Wende nun das Potenzgesetz auf an.
↓ Der Term lässt sich sogar noch weitervereinfachen, indem du die Regel des negativen Exponenten verwendest, das bedeutet
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Wende das Potenzgesetz auf an.
↓ Schreibe .
↓ Wende das Potenzgesetz auf an.
↓ Wende das Potenzgesetz an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Wende das Potenzgesetz an.
↓ Fasse den Exponenten zusammen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Wende das Potenzgesetz auf an.
↓ Fasse den Exponenten von zusammen.
↓ Schreibe .
↓ Verwende die Potenzregel .
↓ Fasse die Basis zusammen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Verwende das Potenzgesetz auf die Basis an.
↓ Verwende das Potenzgesetz auf die Basis an.
↓ Verwende das Potenzgesetz .
↓ Fasse die Basis zusammen.
Hast du eine Frage oder Feedback?
- 3
Fasse so weit wie möglich zusammen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
1. Darstellung
↓ Kürze die Faktoren, die sowohl im Nenner als auch im Zähler vorkommen
2. Darstellung
↓ Potenzgesetze anwenden
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Potenzgesetze
↓ Verwende das Kommutativgesetz, damit du vorne die Zahlen multiplizieren kannst.
↓ Wende das Potenzgesetze zur Multiplikation mit gleicher Basis an.
↓ Verrechne im Exponenten
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Potenzgesetze
↓ Wende die Potenzgesetze (Division bei gleicher Basis) an.
↓ Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
↓ 9 als schreiben
↓ Wende die Potenzrechengesetze bei gleicher Basis an.
↓ Vereinfache die Exponenten
↓ Ausrechnen
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
↓ entspricht
↓ Wende die Potenzrechengesetze an.
Alternativer Lösungsweg
↓ Negative Potenzen werden als Bruch mit im Zähler und mit der Basis der Potenz und positivem Exponent im Nenner dargestellt.
↓ Multiplizieren
↓ Potenzgesetz: Potenzen gleicher Basis werden dividiert, indem man die Exponenten subtrahiert
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Dieser Term kann nicht weiter zusammengefasst werden, da unterschiedliche Potenzen auftreten. Man kann lediglich den Term anders darstellen, indem ausgeklammert wird. Hier kann ausgeklammert werden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Wende zuerst das Potenzgesetz an. Das Minus im Exponent in Plus setzen, indem der Bruch in einen Kehrbruch umgewandelt wird.
↓ Potenzgesetz anwenden. Beim Multiplizieren die beiden Exponenten addieren.
↓ Kürzen mit
↓ Potenzgesetz anwenden. Das Minus im Exponent von y in Plus setzen, indem der Bruch in einen Kehrbruch umgewandelt wird.
Hast du eine Frage oder Feedback?
- 4
Vereinfach die folgenden Terme.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Da die Basen des Dividenden 10 sind, wende dort das 1. Potenzgesetz an. Achtung, Potenzgesetze bei dem Divisor nicht anwendbar, da es keine Potenzgesetze für Addition und Subtraktion gibt.
↓ ↓ Wende nun das 2. Potenzgesetz an, da Dividend und Divisor die gleiche Basis besitzen
↓ Berechne die Differenz der Potenz.
↓ Potenziere und addiere.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Potenzgesetze anwenden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
↓ In Bruchform umwandeln
↓ Den Hauptnenner bilden (100) und den 1. Bruch auf diesen erweitern.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Potenzgesetze anwenden
↓ Hauptnenner () bilden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Potenzgesetz anwenden
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
↓ Schreibweise als Bruch
↓ ↓ Hast du eine Frage oder Feedback?
- 5
Vereinfache folgenden Term unter Verwendung der Potenzgesetze
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
↓ Da hier nur multipliziert wird, kannst du das 1. Potenzgesetz, bei gleichen Basen, immer anwenden
↓ ↓ Die Basen sind zwar unterschiedlich, aber da die Potenzen gleich sind, kannst du hier das 3. Potenzgesetz anwenden.
- 6
Vereinfache die folgenden Ausdrücke mit ganzzahligen Exponenten so weit wie möglich.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Wende die Potenzgesetze an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Schreibe 90 als Potenz mit 3 als Basis.
↓ Wende die Potenzgesetze an.
↓ Klammere aus.
↓ Schreibe 9 in eine 3er Potenz um
↓ Wende die Potenzgesetze an.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Wende die Potenzgesetze an.
↓ in umwandeln damit kürzen möglich ist.
↓ Kürze die Potenzen.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Klammer aus.
↓ Dividiere und wende die Potenzgesetze an.
↓ Klammer auflösen. Nicht vergessen: Vorzeichenänderung
↓ Die Klammer mit negativem Exponenten als Bruch schreiben.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Wende die Potenzgesetze an.
↓ Mit dem Kehrbruch multiplizieren.
↓ Fasse zusammen.
↓ Kürze.
Hast du eine Frage oder Feedback?
Annahme: ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Da größer als ist, kannst du mit dem Kehrwert multiplizieren. Für den Wert von
gilt dann
↓ Potenzen ausmultiplizieren.
↓ Aus allen negativen Werten -1 ausklammern.
↓ Faktorenzerlegung von
↓ Klammern auflösen.
↓ Weiter vereinfachen.
↓ Nenner zusammenfassen.
↓ Potenzen mit der Basis -1 zusammenfassen.
↓ Negative Exponenten in einen Bruch umwandeln.
Weil eine gerade Zahl ist, ist , und daher kann man das Ergebnis auch als oder als schreiben.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Potenzgesetze anwenden.
↓ Potenzgesetze im Zähler anwenden.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Klammer nach Potenzgesetzen auflösen.
↓ Division in Bruchschreibweise darstellen.
↓ Wandle den Doppelbruch um.
↓ Zu einem Bruch zusammenfassen.
↓ Exponenten zusammenfassen.
↓ Kürze mithilfe der Regeln für Potenzgesetze.
↓ Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Den zweiten Bruch mit erweiteren.
↓ mit Hilfe der Potenzgesetze mit dem Zähler multiplizieren.
↓ Den dritten Bruch mit erweiteren.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Potenzgesetz anwenden.
↓ Klammer auflösen.
↓ Potenzgesetz anweden.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Den Bruch in der runden Klammer mit 2 erweitern.
↓ Potenzgesetz anwenden.
↓ ↓ Potenzgesetz anwenden.
↓ Runde Klammer: Hauptnenner bilden.
↓ Potenzgesetz anwenden.
↓ ↓ Im Nenner (-1) ausklammern.
↓ mit kürzen.
Hast du eine Frage oder Feedback?
Gib die Lösung so an, dass sie keine negative Exponenten enthält.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Potenzgesetze anwenden.
Hast du eine Frage oder Feedback?
- 7
Schreibe als Dezimalzahl.
- 8
Gesucht sind Potenzen mit negativen oder positiven Exponenten. Kreuze jeweils alle richtigen Antworten an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Es gibt zwei Lösungen:
Hast du eine Frage oder Feedback?
- 9
Atome sind überall
Ein Heliumatom besitzt einen Durchmesser von etwa Meter, ein Wasserstoffatom wiegt etwa Kilogramm.
Die Masse des Jupiters beträgt etwa kg , wovon etwa kg Wasserstoff sind.
Welche Vorstellung kann man sich von der Größe der Atome und ihrer Masse machen?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Ein Wasserstoffatom hat ungefähr den Durchmesser von .
Die Zehnerpotenz kann man auch als Bruch schreiben. Das sieht dann so aus:
also sind sechs einhundert Milliardstel Meter.
Stell dir vor, du würdest einen Millimeter auf dem Lineal nochmal in Millionen Teile teilen. Davon nimmt man Teile. Dann ist man bei der Größe eines Atoms.
Jetzt steht im Nenner des Bruchs eine mit Nullen. Diese Zahl nennt man auch Quadrilliarde. Ein Atom wiegt also ungefähr ein quadrilliardstel Kilogramm. Stell dir vor du nimmst einen gestrichenen Teelöffel mit Backpulver.
Dieser wiegt etwa g, also wiegt ein halber Teelöffel etwa g. Dieses kleine Häufchen Backpulver teilst du in eine Billionen Häufchen. Aber damit nicht getan. Eines dieser Häufchen teilst du nochmals in eine Billionen kleinere Häufchen. Die Masse eines dieser zwei Mal geteilten entspricht in etwa der Masse eines Wasserstoffatoms. Das ist eine unvorstellbar kleine Zahl!
Hast du eine Frage oder Feedback?
Berechne die Anzahl der Wasserstoffatome, die der Jupiter enthält.
Verwende für die Lösung folgende Schreibweise: Basis^Exponent
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
Die Masse des Wasserstoffanteils des Jupiters beträgt und die Masse eines Wasserstoffatoms: .
Teilt man nun die Masse des Wasserstoffanteils im Jupiter durch die Masse eines Wasserstoffatoms, so erhält man die Anzahl an Atomen.
Aus diesem Bruch kann man die Einheit kg und die direkt kürzen, da sie als Produkt im Zähler und im Nenner stehen.
Wende nun das Potenzgesetz zum Dividieren von Potenzen mit gleicher Basis an
Der Jupiter enthält also die unglaublich hohe Anzahl von Wasserstoffatomen!
Diese Zahl nennt man übrigens Nonillion.
Hast du eine Frage oder Feedback?
- 10
Ordne die Potenzen richtig zu.
- 11
Markiere alle Terme, die das Gleiche beschreiben. Man nennt sie auch "äquivalent".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
Die äquivalenten Terme sind:
Der Term kann mit den Potenzgesetzen nicht so umgeformt werden, dass er äquivalent zu den anderen Termen ist.
Ebenso bedeutet der Term
auch nicht das gleiche wieHast du eine Frage oder Feedback?
Versuche, die Terme mithilfe der Potenzgesetze umzuformen. Möglicherweise sind manche von ihnen dann gleich.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
Die äquivalenten Terme sind:
Der Term ist keine Potenz und beschreibt auch nicht das gleiche wie .
Hast du eine Frage oder Feedback?
Forme die Terme mithilfe der Potenzgesetze um. Möglicherweise sind einige von ihnen dann gleich.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
Die äquivalenten Terme sind:
Der Term beschreibt . Der Exponent hat sich verändert und der Term beschreibt nicht das Gleiche wie .
Hast du eine Frage oder Feedback?
Forme die Terme mithilfe der Potenzgesetze um. Möglicherweise sind einige von ihnen dann gleich.
- 12
Berechne die Potenzaufgaben und ordne die Lösungen richtig zu.
Beachte die Rechenregeln für Potenzen.
- 13
Berechne die Potenzaufgaben und ordne die Lösungen richtig zu.
Benutze die Potenzgesetze.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?