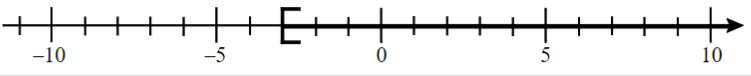2020
Die Aufgaben findest du hier zum Ausdrucken als PDF.
- 1
Berechne
- 2
Zeichne die Menge L = {x | x ≥ –3} auf der Zahlengerade ein (G = ).

- 3
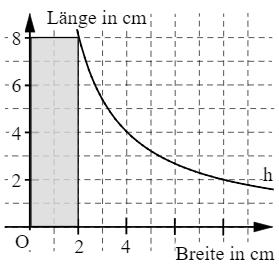
Mithilfe des dargestellten Hyperbelastes h kannst du Rechtecke mit demselben Flächeninhalt zeichnen. Ein solches Rechteck ist bereits eingezeichnet. Bestimme anhand der Zeichnung die Seitenlänge des Quadrats mit demselben Flächeninhalt.
- 4
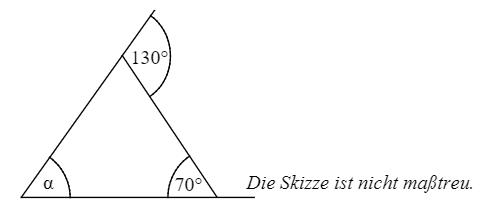
Gib das Winkelmaß α an.
- 5
Miriam bekommt die Lösung für eine Aufgabe beim „Lernen zuhause“ von ihrer Lehrerin geschickt. Leider ist nach dem Ausdrucken ein Teil der Gleichung nicht sichtbar. Ergänze die Gleichung, sodass die Lösungsmenge L ={4} ist (G = ).
2x + 8x =
- 6
Berechne den Wert der Determinante.
- 7
Zur Berechnung des Flächeninhalts A des Parallelogramms ABCD (siehe Skizze) wurde die Determinante aufgestellt:
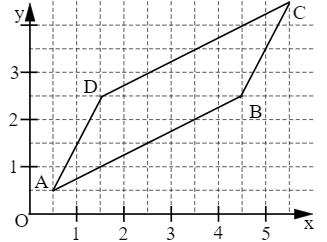
Kreuze die dazu verwendeten Pfeile an.
- 8
Das Dreieck ABC wird durch Parallelverschiebung auf das Dreieck A ́B ́C ́abgebildet. Vervollständige das Dreieck A ́B ́C ́.
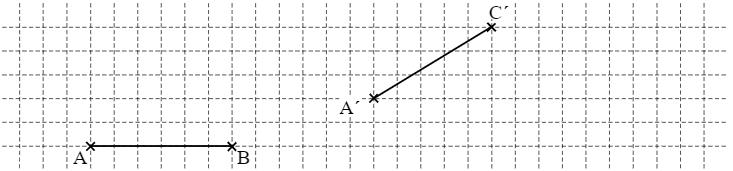
- 9
Susi legt 500 € zu einem Jahreszinssatz von 1,5 % an. Wie viel Zinsen bekommt sie nach Ablauf eines Jahres?
€ - 10
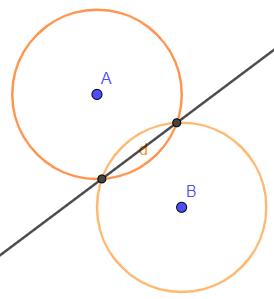
Zeichne alle Punkte ein, die von den Punkten A und B gleich weit entfernt sind.

- 11
Kreuze den Term an, der zum Term T(x) = 4x² –2 äquivalent ist (G = ).
- 12
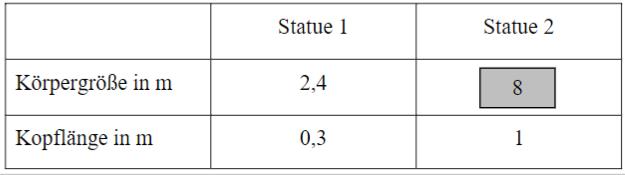
Bei Statuen im antiken Griechenland war das Verhältnis der gesamten Körpergröße zur Kopflänge immer gleich. Ergänze in der Tabelle den Wert für die Körpergröße der Statue 2.
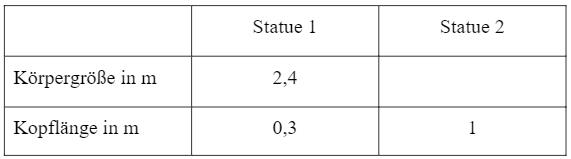
- 13
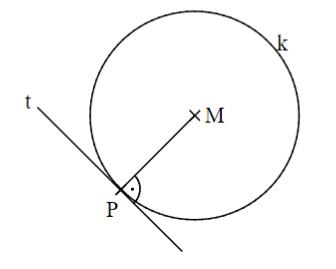
Zeichne im Punkt P die Tangente t an den Kreis k.
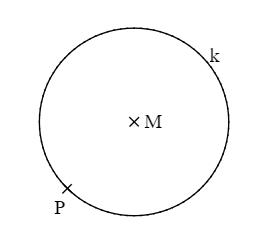
- 14
Ein Rechteck hat die Länge l= 7cm und die Breite b = 4cm. Es entsteht ein neues Rechteck, indem man die Länge um x cm vergrößert und die Breite unverändert lässt. Der Flächeninhalt dieses Rechtecks soll genau 60 cm² sein. Gib eine Gleichung an, die diesen Sachverhalt beschreibt ().
- 15
Tim arbeitet in einem Elektronikladen und hat ein Diagramm über die verkauften Webcams gefunden. Stolz sagt er seinem Chef: „Wir haben im März fast dreimal so viele Webcams verkauft wie im Februar!“ Begründe, warum diese Aussage nicht richtig ist.
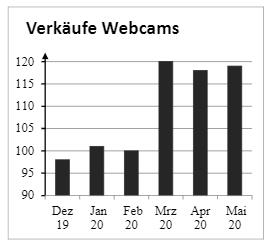
- 16
Kreuze die Lösung folgender Ungleichung an (G = ).
- 17
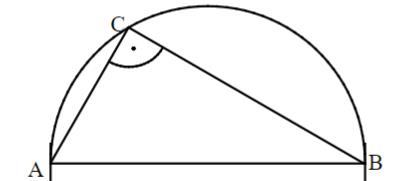
Gegeben ist das rechtwinklige Dreieck ABC. Zeichne die Ortslinie ein, auf der alle Punkte C liegen, so dass das Dreieck ABC rechtwinklig ist und die Hypotenuse hat.
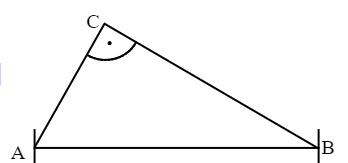
- 18
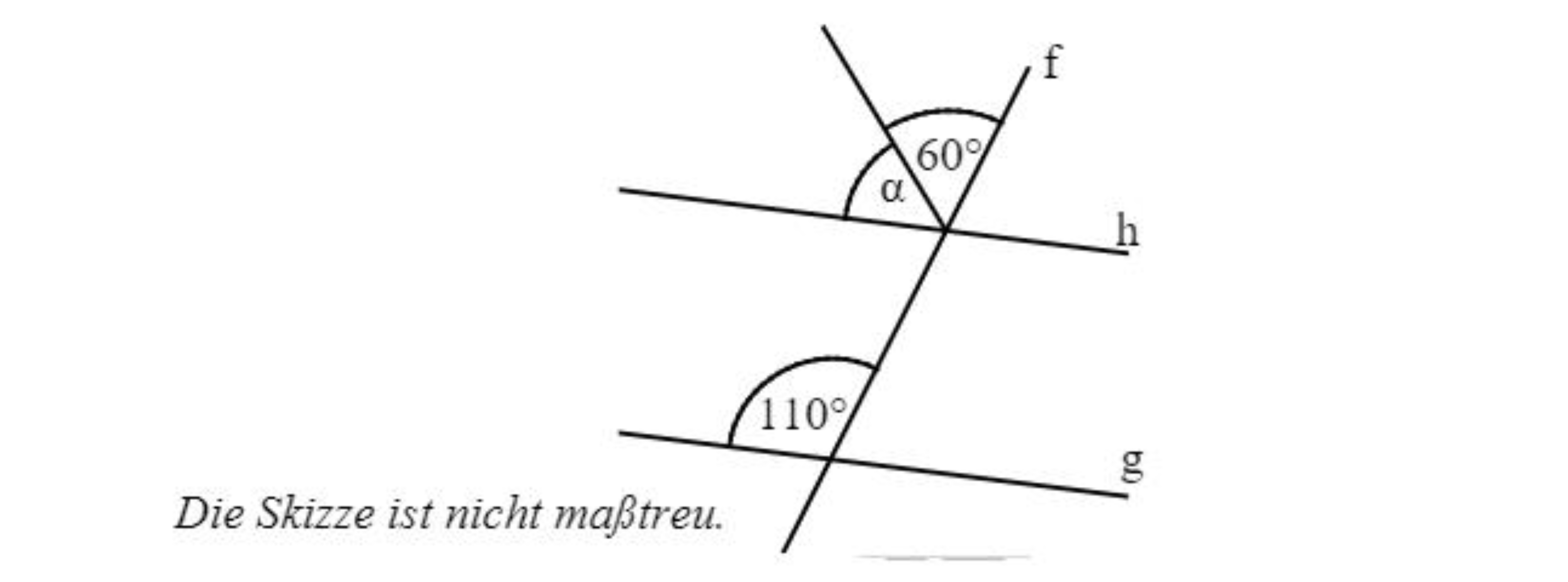
Die Gerade f schneidet die parallelen Geraden g und h. Gib das Winkelmaß α an.
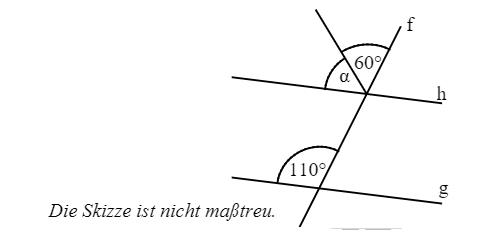 °
° - 19
28 Schülerinnen und Schüler der Klasse 8a erzielten in der 1. Schulaufgabe im Fach Mathematik einen Notendurchschnitt von 3,0. Ergänze die fehlenden Einträge in der Notentabelle.

- 20
Die Gerade f schneidet die Geraden g und h (siehe Abbildung). Für die Winkelmaße gilt: α = 62°, β = 118°. Kreuze die zutreffende Aussage an.
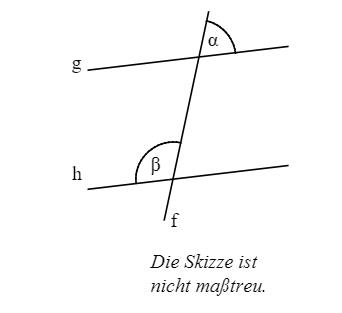
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?