2020 - lernen mit Serlo!

1

Gegeben ist der quadratische Term $\mathrm{T(x) = – (x + 3)² + 5\ \ (G=\mathbb{Q})}$ . Welche der folgenden Angaben gibt den Extremwert mit der dazugehörigen Belegung von $\text{x}$ für diesen Term an?

Kreuze an.

$\mathrm{T_{max}}= –1\ \ \text{für}\ \ x = –5$
$\mathrm{T_{min}}= 3\ \ \text{für}\ \ x = –5$
$\mathrm{T_{max}}= 5\ \ \text{für}\ \ x = –3$
$\mathrm{T_{min}}= 5\ \ \text{für}\ \ x = –1$

2

Löse die Klammer auf und fasse so weit wie möglich zusammen $\ \ (\mathbb{G=Q}).$

$\ (x-2y)^2-6xy=$

3

Der Faktor $\ –6 \$ wurde ausgeklammert.

Vervollständige.

$\ -6x^2+12xy-18=-6\cdot(\hspace{25mm})$

4

Bestimme die Lösungsmenge der folgenden Gleichung $\ \ \mathbb{(G=Q)}$ .

$\ \mathrm{4x+x^2=(x+1)\cdot(x+2)}$

$\ \boxed{\mathbb{L}=\{\qquad\}}$

5

Vergrößert man den Zähler des Bruches $\ \dfrac{1}{2}\$ um $\ 3\$ und den Nenner um $\ 2\$ , so entsteht ein neuer Bruch.

Kreuze an, so dass eine wahre Aussage entsteht.

Der Wert des neuen Bruchs ist:

halb so groß wie der Wert des ursprünglichen Bruches
genau so groß wie der Wert des ursprünglichen Bruches
doppelt so groß wie der Wert des ursprünglichen Bruches
dreimal so groß wie der Wert des ursprünglichen Bruches

6

Gegeben sind folgende Wertetabellen.

Tabelle A

x	2	4	7
y	3	6	10,5

Tabelle B

x	1	2	3
y	2,5	4,5	7,5

Welche der Tabellen stellt einen direkt proportionalen Zusammenhang dar?

Kreuze an.

Tabelle A
Tabelle B
Tabelle A und Tabelle B
keine der beiden Tabellen

7

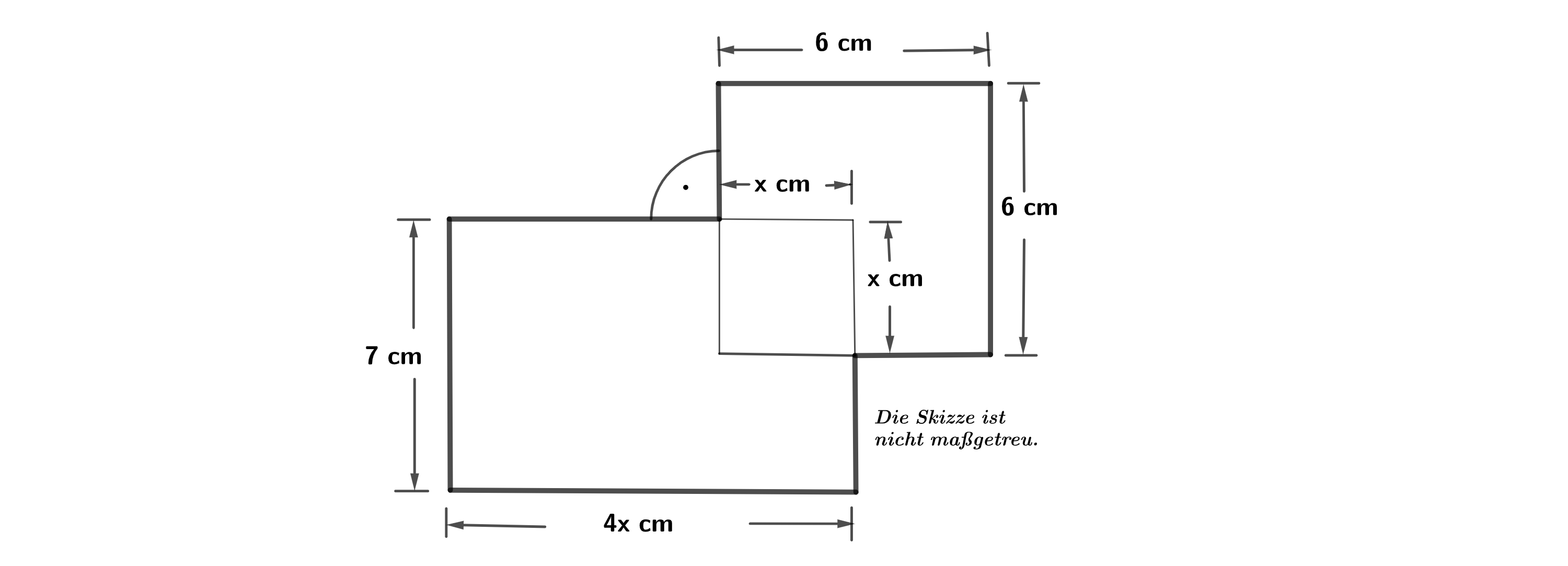
Eine Figur besteht aus einem Rechteck und einem Quadrat, die sich zum Teil überdecken (siehe Skizze). Wie lässt sich der Flächeninhalt A der dick umrandeten Figur in Abhängigkeit von x darstellen? $\ \mathbb{(G=Q)}$

Kreuze an.

$A(x)=\mathrm{[7\cdot4x+x^2]cm^2}$
$A(x)=\mathrm{[7+4x+x+6+6+x]cm^2}$
$A(x)=\mathrm{[7\cdot4x+36-x^2]cm^2}$
$A(x)=\mathrm{[7\cdot4x+36]cm^2}$

8

Marcus sagt: „Ich denke an ein besonderes Viereck mit folgenden Eigenschaften:

$\hspace{25mm}$ - Das Viereck hat genau zwei Symmetrieachsen.

$\hspace{25mm}$ - Die Diagonalen stehen aufeinander senkrecht.

$\hspace{25mm}$ - Das Viereck ist punktsymmetrisch.“

Gib an, welches Viereck Marcus beschreibt.

Markus beschreibt $\ \rule{4.5cm}{0.1mm}$ .

9

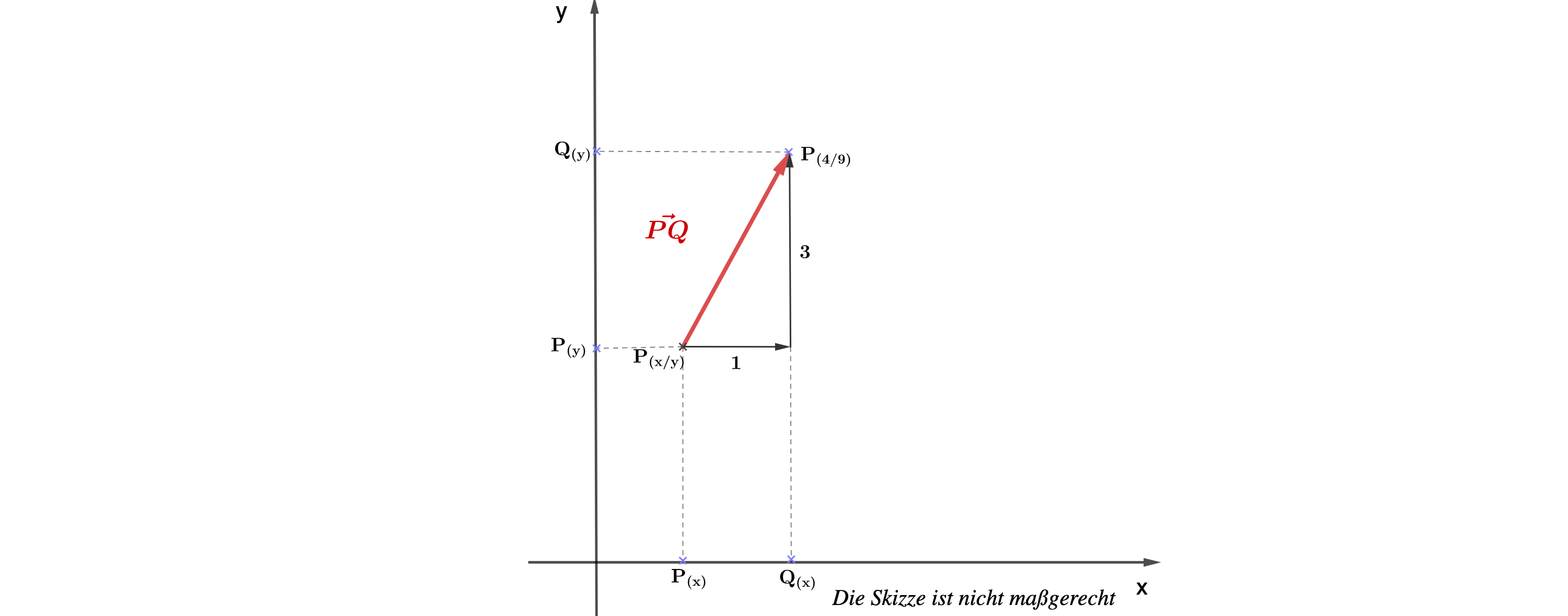
Berechne die Koordinaten des Punktes

$\mathrm{P(x|y)}\$ mit $\ \mathrm{x,\ y}\in\ \mathbb{Q},\$ wenn gilt:

$\mathrm{Q(4|9)}\$ und $\ \overrightarrow{PQ}=\begin{pmatrix} 1 \\ 3 \end{pmatrix}$

$\ \boxed{\text{P}(\qquad|\qquad)}$

10

Ein Legespiel besteht aus weißen und schwarzen Karten (siehe Skizze). Klaus soll so viele schwarze Karten wegnehmen, dass anschließend nur noch 80 % der verbleibenden Kartenschwarz sind.

Gib an, wie viele schwarze Karten Klaus entfernen muss.

Karten

11

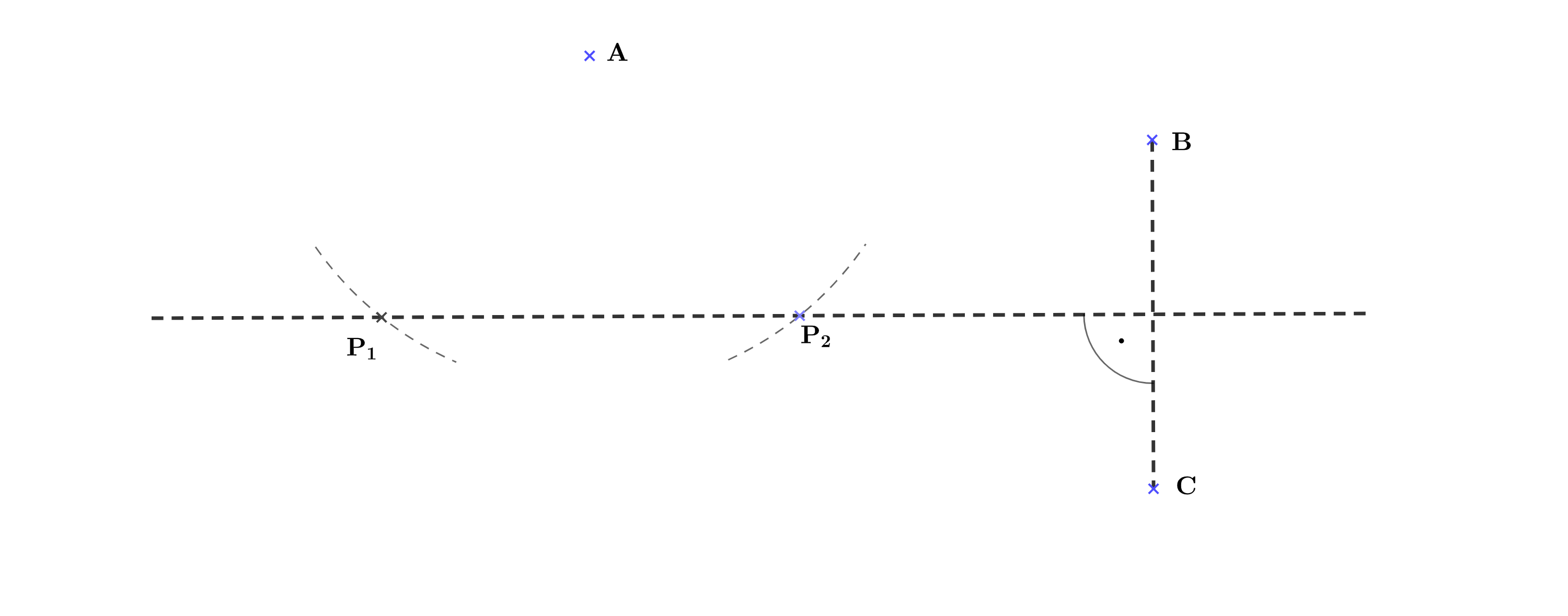
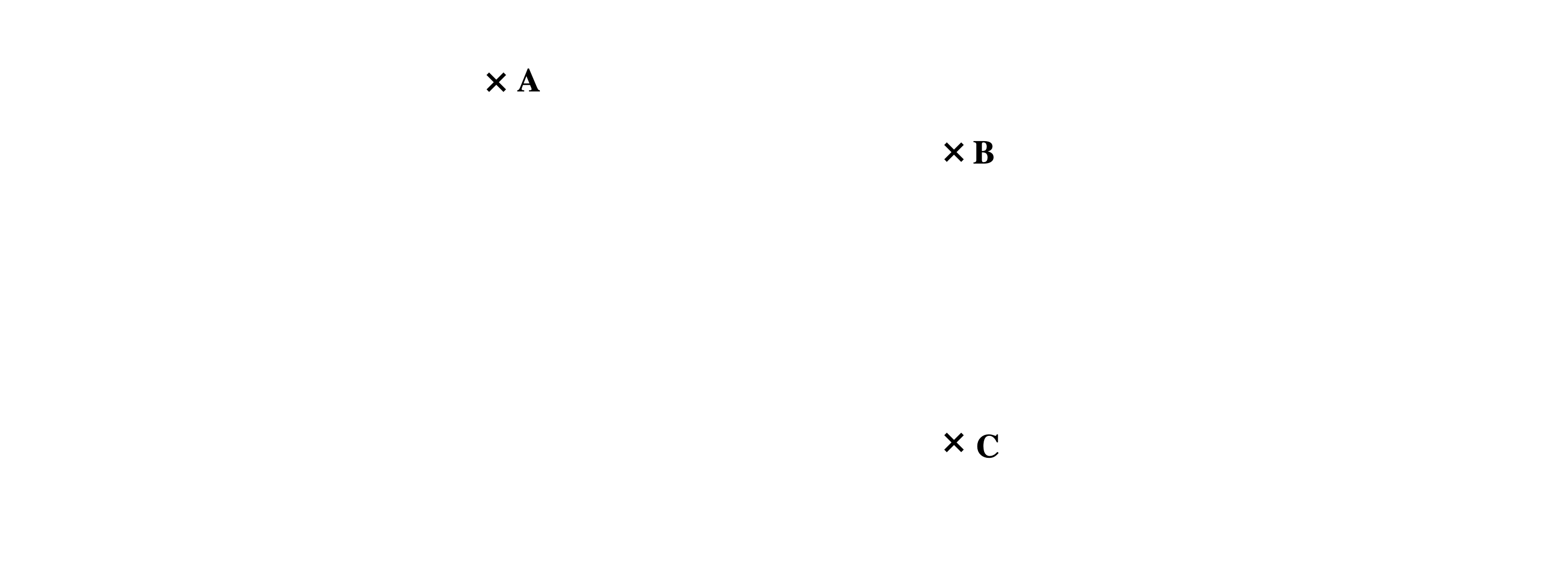
Markiere alle Punkte $\ \mathrm{P_n}\,$ , die von den Punkten $\ \text{B}\$ und $\ \text{C}\$ gleich weit entfernt sind und zugleich eine Entfernung von $\ \mathrm{3\ cm}\$ vom Punkt $\ \text{A}\$ haben.

12

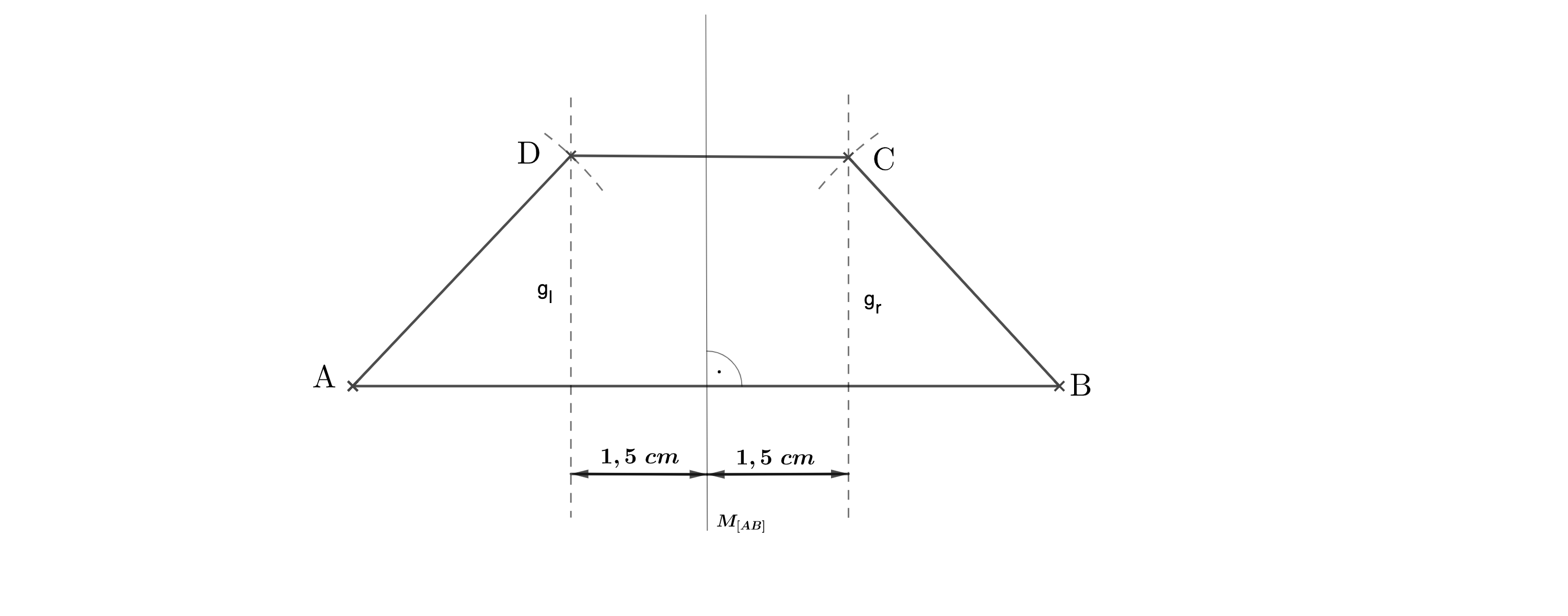
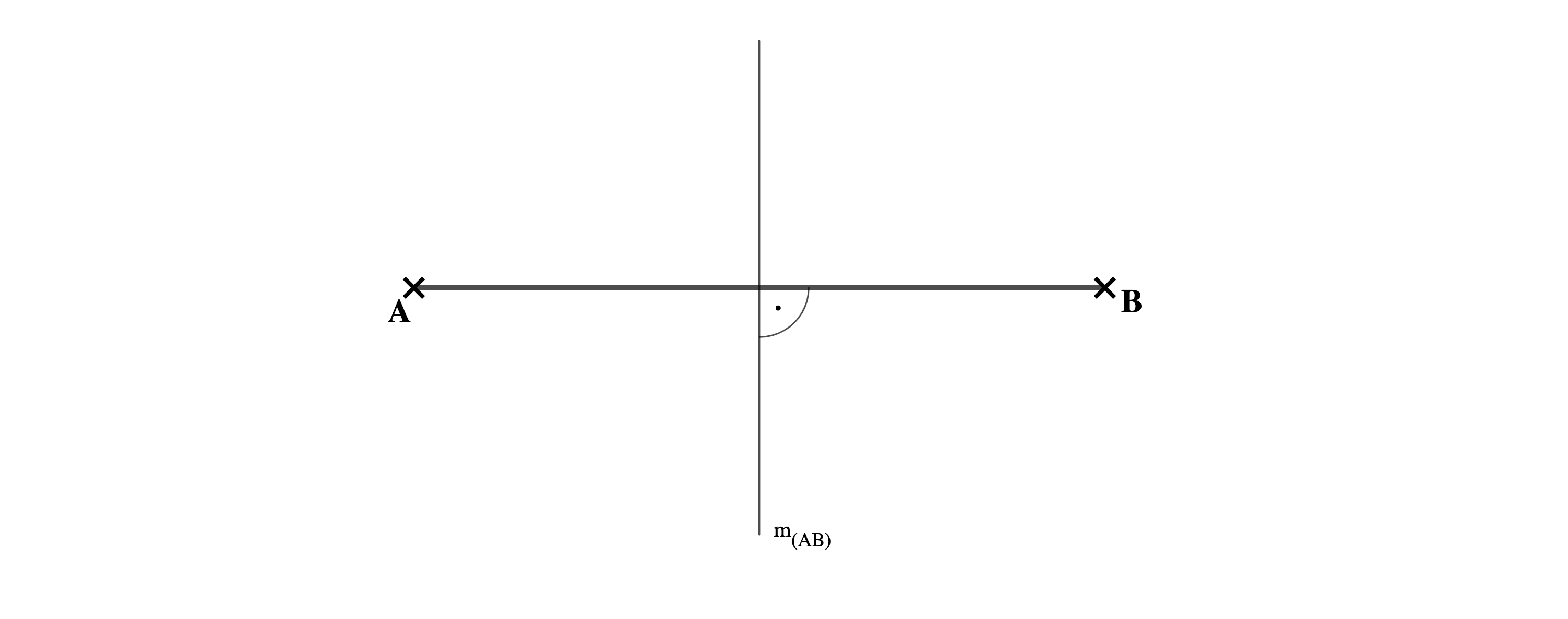
Gegeben ist die Strecke $\ \text{[AB]}\$ mit der Mittelsenkrechten $\ \mathrm{m_{[AB]}}.\$

Für das gleichschenklige Trapez $\ \text{ABCD}\$ gilt:

$\ \mathrm{\overline{CD} = 3\ cm}$ und $\ \mathrm{\overline{AD} = 2\ cm.}\$

Ergänze die Strecke $\ \text{[AB]}\$ zum gleichschenkligenTrapez $\ \text{ABCD}.$

13

Gegeben ist der Term $\ \ \mathrm{T(x)=\dfrac{x-2}{(3+x)\cdot x}}\ \ \mathbb{(G=Q).}$

Kreuze an, welche Definitionsmenge zu diesem Term gehört.

$\mathbb{D=Q}\backslash\{-3;2\}$
$\mathbb{D}=\{-3;0\}$
$\mathbb{D=Q}\backslash\{0\}$
$\mathbb{D=Q}\backslash\{-3;0\}$
$\mathbb{D}=\{-3;2\}$

14

Bestimme die Lösungsmenge $\ \mathbb{L}\$ der Bruchgleichung $\ \dfrac{4}{x+3}=\dfrac{1}{x}\ , \ \mathbb{D=Q}\backslash\{-3;0\}$

$\ \boxed{\mathbb{L}=\{\hspace{10mm}\}}$

15

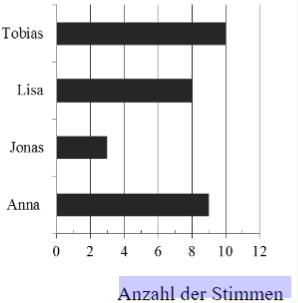
Das Diagramm unten stellt das Ergebnis der letzten Klassensprecherwahl dar. Jede Schülerin / jeder Schüler hatte genau eine Stimme. Zwei der folgenden Aussagen treffen zu.

Kreuze diese an.

$\dfrac{1}{10}\$ der Klasse hat Jonas gewählt
Die beiden Jungen Jonas und Tobias bekamen zusammen mehr als die Hälfte der Stimmen.
Genau $\ \dfrac{2}{3}\$ der Kinder in der Klasse haben Anna nicht gewählt.
Lisa bekam mehr als $\ 20\%\$ der Stimmen.

16

Mit dem abgebildeten Achterwürfel (Zahlen $1$ bis $8$ ) wird einmal gewürfelt.

Gib die Wahrscheinlichkeit für das Ereignis „Die gewürfelte Zahl ist durch $2$ und zugleich durch $3$ teilbar“ an.

17

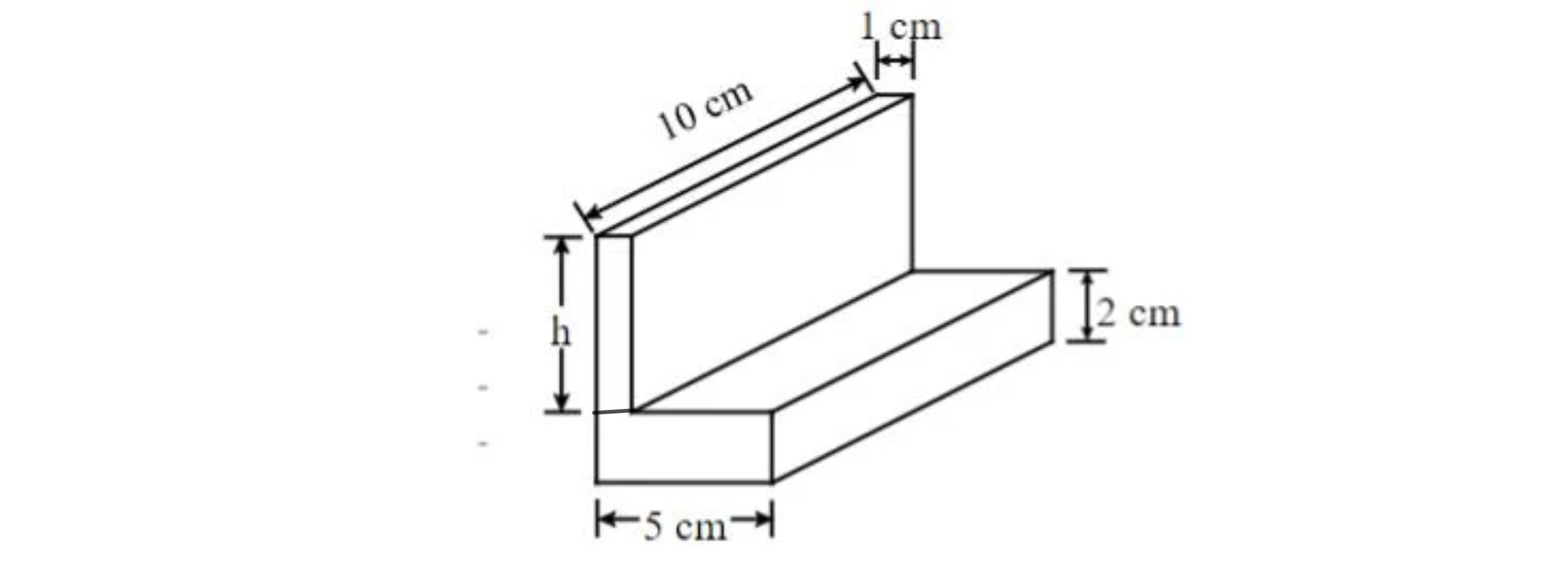
Zur Herstellung eines L-Profils (siehe Skizze) wurde ein kleiner Quader aus einem größeren Quader geschnitten. Das L-Profil hat ein Gesamtvolumen von $\ \mathrm{130\ cm³}\$ .

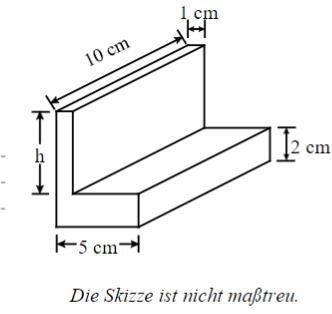
Gib das Maß für die Höhe h an.

cm

18

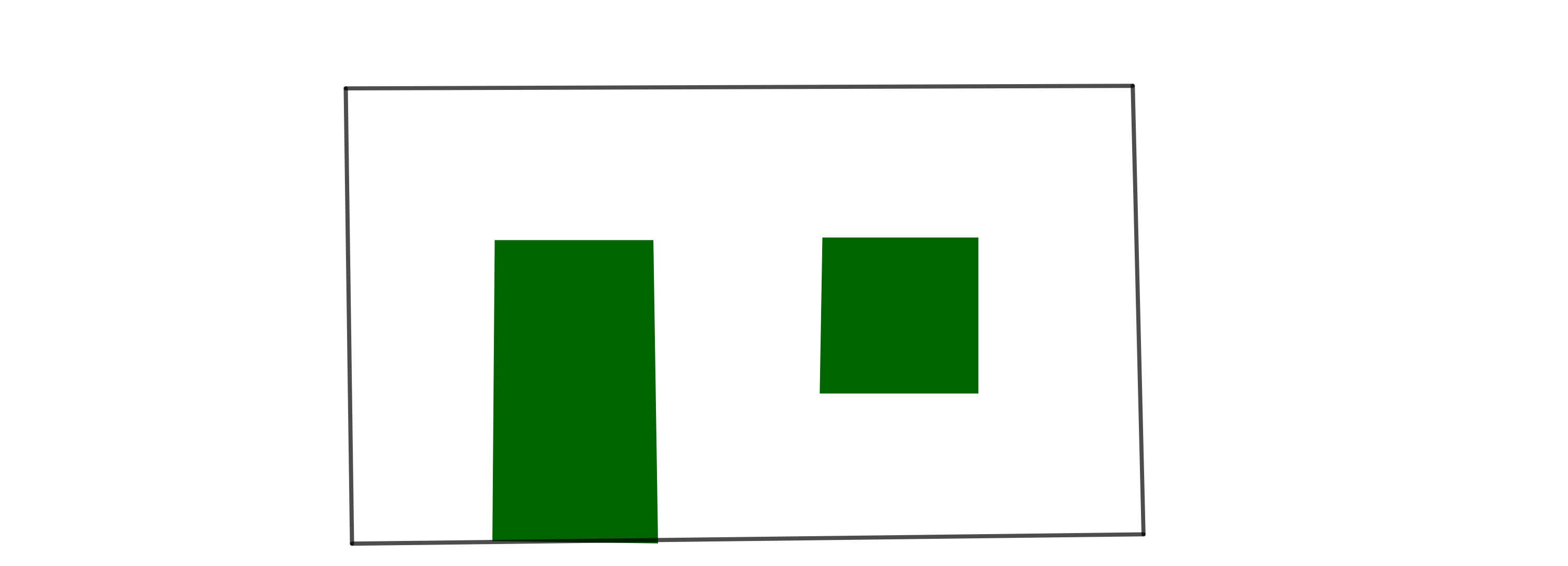
Die maßstabsgetreue Skizze zeigt eine Badezimmerwand mit einer Tür und einem Fenster. Das Fenster ist quadratisch und hat einen Flächeninhalt von 1 m².

Wie viele Päckchen Fliesen müssen gekauft werden, um die Wand vom Boden bis zu einer Höhe von 2 m zu fliesen, wenn in einem Päckchen Fliesen für 2 m² enthalten sind?

Gib deinen Lösungsweg an.

19

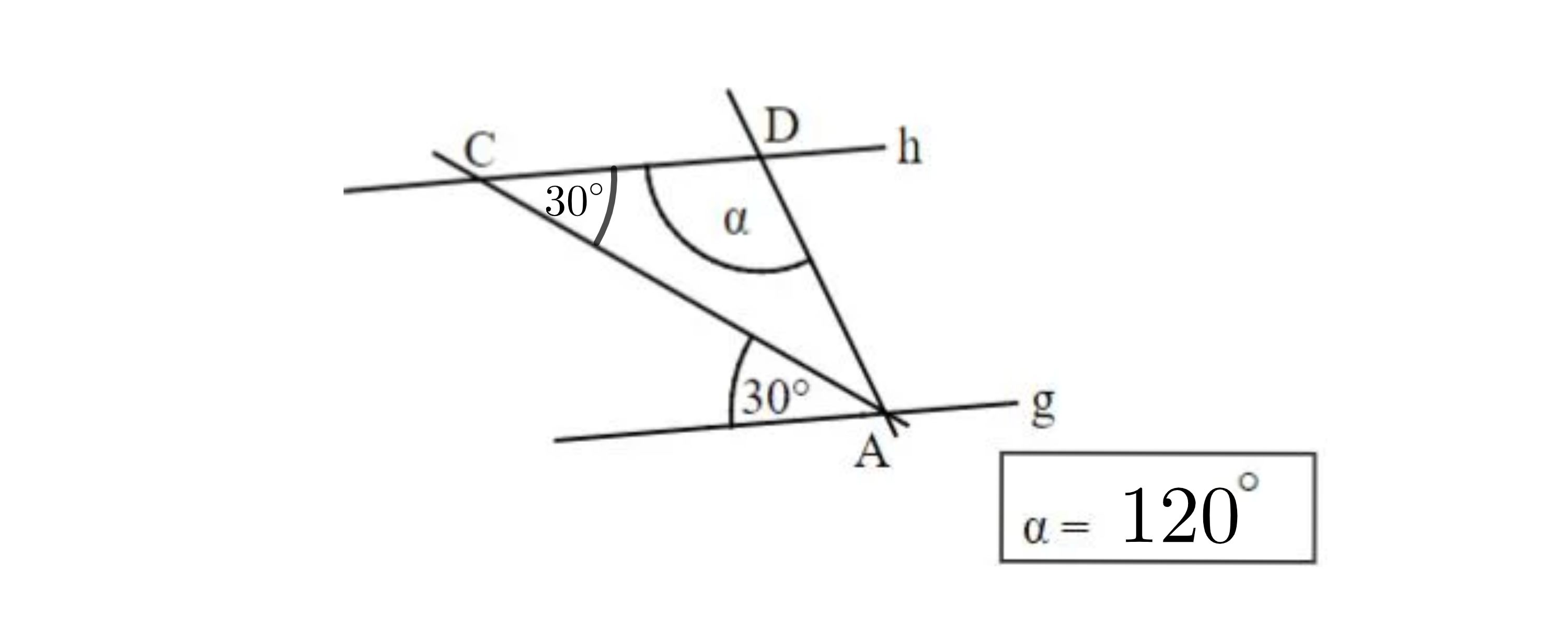
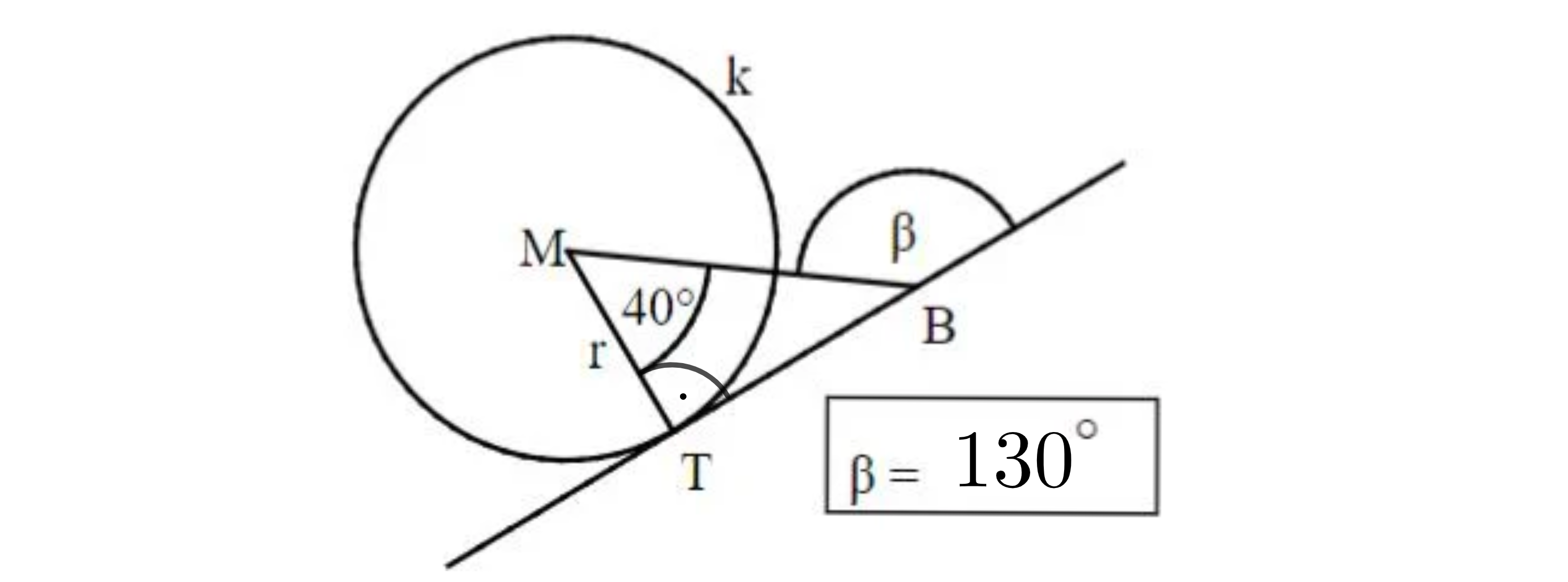
Gib die Winkelmaße $\ α\$ und $\ β\$ an.

Die Skizzen sind nicht maßtreu.

Es gilt: $\ \mathrm{g \Vert h}\$ und $\ \mathrm{\overline{AD}=\overline{CD}}$
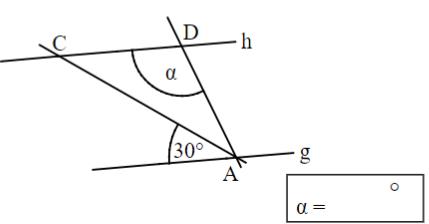
Es gilt: $\ \text{BT}\$ ist Tangente an den Kreis $\ \text{k(M; r)}\$ mit dem Berührpunkt $\ \text{T}\$ .

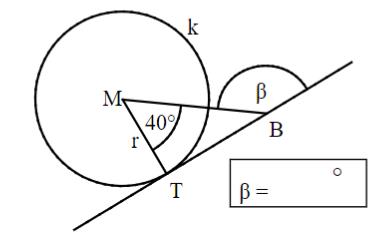
20

Der Flächeninhalt $\ \text{A}\$ eines Rechtecks beträgt $\ \mathrm{200\ cm^2}.\$ Die Länge $\ \text{l}\$ des Rechtecks ist doppelt so groß wie seine Breite $\ \text{b.}\$

Gib die Breite $\ \text{b}\$ des Rechtecks an.

cm

21

Von dem Dreieck $\ \text{ABC}\$ sind die Maße $\ \mathrm{a = 5\ cm}\$ und $\ \mathrm{b = 3\ cm}\$ bekannt.

Begründe, warum die Seitenlänge $\ \text{c}\$ mehr als $\ \mathrm{2\ cm}\$ betragen muss.

22

Der Preis eines Schokoriegels wurde um $\ 10\%\$ auf $\ 0{,}55 €\$ angehoben.

Gib an, wie viel der Schokoriegel vor der Preiserhöhung gekostet hat.

€