Aufgaben mit zwei Kugeln

Hier findest du Aufgaben zu Kugeln. Lerne, die gegenseitige Lagebeziehung zwischen Kugeln zu untersuchen!

Gegeben sind zwei Kugeln $K_1$ mit $M_1(2\left|4\right|5)$ und $r_1=3$ und $K_2$ mit $M_2(1\left|-2\right|4)$ und $r_2=5$ .

Zeige, dass die beiden Kugeln $K_1$ und $K_2$ sich schneiden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugelgleichung
Lagebeziehung der beiden Kugeln
Gegeben sind die beiden Kugelradien: $r_1=3$ und $r_2=5$
Berechne:
$|r_1-r_2|=|3-5|=|-2|=2$
$d(M_1M_2)=\Big\vert\overrightarrow{M_1M_2}\Big\vert$
$r_1+r_2=3+5=8$
Zu 2. Berechne den Vektor $\overrightarrow{M_1M_2}=\begin{pmatrix} 1 \\ -2 \\4 \end{pmatrix}-\begin{pmatrix} 2 \\ 4 \\ 5 \end{pmatrix}=\begin{pmatrix} -1 \\-6 \\ -1 \end{pmatrix}$
Berechne $d(M_1M_2)=\Big\vert\overrightarrow{M_1M_2}\Big\vert=\sqrt{(-1)^2+(-6)^2+(-1)^2}=\sqrt{38}\approx6{,}2$
Setze die berechneten Werte in die Schnittpunktsbedingung ein:
$|r_1-r_2|<d(M_1M_2)<r_1+r_2\;\;\Rightarrow\;\;2<6{,}2<8$
Antwort: Die Schnittpunktsbedingung ist erfüllt, d.h. die beiden Kugeln schneiden sich.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Ist der Betrag der Differenz der beiden Kugelradien kleiner als der Abstand der beiden Kugelmittelpunkte und dieser Abstand wiederum kleiner als die Summe der beiden Kugelradien, dann schneiden sich die beiden Kugeln.
Schnittpunktsbedingung: $|r_1-r_2|<d(M_1M_2)<r_1+r_2$

Bestimme eine Gleichung der Schnittebene $E$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugelgleichung

Aufstellen der Kugelgleichungen

Kugel $K_1$ :

$\textcolor{ff6600}{M_1(2|4|5)}$ , $\textcolor{006400}{r_1=3}$

$K_1:\ (\vec{x}-\textcolor{ff6600}{\vec{m_1}})^2=\textcolor{006400}{r_1}^2$

Setze $\textcolor{ff6600}{ M_1}$ und $\textcolor{006400}{r_1}$ in $K$ ein.
	↓
$\displaystyle K_1:\ \left(\vec x-\textcolor{ff6600}{\begin{pmatrix}2\\4\\5\end{pmatrix}}\right)^2$	$=$	$\displaystyle \textcolor{006400}{3}^2$
	↓	Vereinfache.
$\displaystyle \left(\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}-\begin{pmatrix}2\\4\\5\end{pmatrix}\right)^2$	$=$	$\displaystyle 9$
	↓	Fasse zusammen.
$\displaystyle \begin{pmatrix}x_1-2\\x_2-4\\x_3-5\end{pmatrix}^2$	$=$	$\displaystyle 9$
	↓	Rechne das Skalarprodukt aus.
$\displaystyle (x_1-2)^2+(x_2-4)^2+(x_3-5)^2$	$=$	$\displaystyle 9$
	↓	Vergiss nicht die binomische Formel anzuwenden.
$\displaystyle x_1^2-4x_1+4+x_2^2-8x_2+16+x_3^2-10x_3+25$	$=$	$\displaystyle 9$
	↓	Fasse die linke Seite zusammen.
$\displaystyle x_1^2+x_2^2+x_3^2-4x_1-8x_2-10x_3+45$	$=$	$\displaystyle 9$	$\displaystyle -45$
$\displaystyle x_1^2+x_2^2+x_3^2-4x_1-8x_2-10x_3$	$=$	$\displaystyle -36$

Antwort: Die Gleichung der Kugel $K_1$ lautet: $x_1^2+x_2^2+x_3^2-4x_1-8x_2-10x_3=-36$

Kugel $K_2$ :

$\textcolor{ff6600}{M_2(1|-2|4)}$ , $\textcolor{006400}{r_2=5}$

$K_2:\ (\vec{x}-\textcolor{ff6600}{\vec{m_2}})^2=\textcolor{006400}{r_2}^2$

Setze $\textcolor{ff6600}{ M_2}$ und $\textcolor{006400}{r_2}$ in $K$ ein.
	↓
$\displaystyle K_2:\ \left(\vec x-\textcolor{ff6600}{\begin{pmatrix}1\\-2\\4\end{pmatrix}}\right)^2$	$=$	$\displaystyle \textcolor{006400}{5}^2$
	↓	Vereinfache.
$\displaystyle \left(\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}-\begin{pmatrix}1\\-2\\4\end{pmatrix}\right)^2$	$=$	$\displaystyle 25$
	↓	Fasse zusammen.
$\displaystyle \begin{pmatrix}x_1-1\\x_2+2\\x_3-4\end{pmatrix}^2$	$=$	$\displaystyle 25$
	↓	Rechne das Skalarprodukt aus.
$\displaystyle (x_1-1)^2+(x_2+2)^2+(x_3-4)^2$	$=$	$\displaystyle 25$
	↓	Vergiss nicht die binomische Formel anzuwenden.
$\displaystyle x_1^2-2x_1+1+x_2^2+4x_2+4+x_3^2-8x_3+16$	$=$	$\displaystyle 25$
	↓	Fasse die linke Seite zusammen.
$\displaystyle x_1^2+x_2^2+x_3^2-2x_1+4x_2-8x_3+21$	$=$	$\displaystyle 25$	$\displaystyle -21$
$\displaystyle x_1^2+x_2^2+x_3^2-2x_1+4x_2-8x_3$	$=$	$\displaystyle 4$

Antwort: Die Gleichung der Kugel $K_2$ lautet: $x_1^2+x_2^2+x_3^2-2x_1+4x_2-8x_3=4$

Schnitt der beiden Kugeln berechnen

Die Kugel $1$ entspricht Gleichung $\mathrm{(I)}$ und die Kugel $2$ entspricht Gleichung $\mathrm{(II)}$ . Es handelt sich hier um ein Gleichungssystem mit 2 Gleichungen und 3 Variablen.

Berechne die Differenz der beiden Gleichungen.

$\def\arraystretch{1.25} \begin{array}{cccccccl}\mathrm{(I)}:&x_1^2 & + & x_2^2 & + &x_3^2 &-&4x_1&-&8x_2&-&10x_3& = & -36 & \\-\mathrm{(II)}:&x_1^2 & + & x_2^2 & + &x_3^2 &-&2x_1&+&4x_2&-&8x_3& = &\ \;\;\;\;4 &\end{array}\\\overline{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;+\;\;\;\;0\;\;\;+\;\;\;\;0\;\;\;\;-\;\;\;2x_1\;\;\;-\;\;12x_2\;-\;\;\;2x_3\;\;\;\;=\;\;\;-40}$

$\displaystyle -2x_1-12x_2-2x_3$	$=$	$\displaystyle -40$	$\displaystyle :(-2)$
$\displaystyle x_1+6x_2+x_3$	$=$	$\displaystyle 20$

Antwort: Die Gleichung der Schnittebene lautet $E:\; x_1+6x_2+x_3=20$ .

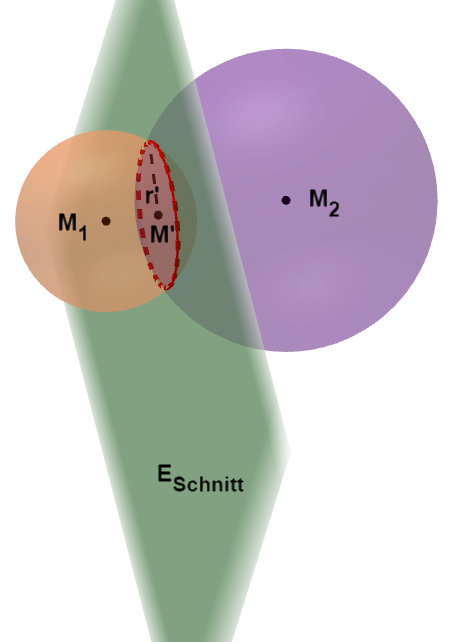
Zwei Kugeln mit Schnittebene und Schnittkreis

Die nebenstehende Abbildung ist nicht verlangt worden.

Sie dient nur der Veranschaulichung.

Dargestellt sind die Kugeln $K_1$ mit Mittelpunkt $M_1$ und $K_2$ mit Mittelpunkt $M_2$ .

Die Kugeln schneiden sich in einem Schnittkreis (rot), der den Mittelpunkt $M'$ und den Radius $r'$ hat. Der Schnittkreis liegt in der Schnittebene $E$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechne den Mittelpunkt $M'$ des Schnittkreises der beiden Kugeln und den Schnittkreisradius $r'$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenseitige Lage zweier Kugeln

Berechnung des Mittelpunkt $M'$

Stelle die Gleichung der Lotgeraden $g_{Lot}$ durch den Mittelpunkt $M_1$ auf die Ebene $E$ auf.

Verwende als Aufpunkt den Mittelpunkt $M_1$ und als Richtungsvektor den Normalenvektor der Ebene $E$ : $\vec n = \begin{pmatrix}1\\6\\1\end{pmatrix}$

$g_{Lot}:\;\vec X=\begin{pmatrix}2\\4\\5\end{pmatrix}+t\cdot\begin{pmatrix}1\\6\\1\end{pmatrix}$

oder

$g_{Lot}:\;\vec X=\begin{pmatrix}\textcolor{006400}{ x_1}\\\textcolor{ff6600}{x_2}\\\textcolor{660099}{x_3}\end{pmatrix}=\begin{pmatrix}\textcolor{006400}{2+t}\\\textcolor{ff6600}{4+6t}\\\textcolor{660099}{5+t}\end{pmatrix}$

Berechne den Mittelpunkt $M'$ , indem du die Lotgerade $g_{Lot}$ mit der Ebene $E$ schneidest:

$g_{Lot}\cap E $
	↓
$\displaystyle E:\; \textcolor{006400}{x_1}+6\textcolor{ff6600}{x_2}+\textcolor{660099}{x_3}$	$=$	$\displaystyle 20$
	↓	Setze $\textcolor{006400}{x_1=2+t}$ , $\;\textcolor{ff6600}{x_2=4+6t}$ , $\;\textcolor{660099}{x_3=5+t}$ in $E$ ein.
$\displaystyle (\textcolor{006400}{2+t})+6\cdot(\textcolor{ff6600}{4+6t})+(\textcolor{660099}{5+t})$	$=$	$\displaystyle 20$
	↓	Löse die Klammern auf.
$\displaystyle 2+t+24+36t+5+t$	$=$	$\displaystyle 20$
	↓	Fasse zusammen.
$\displaystyle 38t+31$	$=$	$\displaystyle 20$	$\displaystyle -31$
	↓	Löse nach $t$ auf.
$\displaystyle 38t$	$=$	$\displaystyle -11$	$\displaystyle :38$
$\displaystyle t$	$=$	$\displaystyle -\dfrac{11}{38}$

Zur Berechnung des Mittelpunktes $M'$ setzt du $t=-\dfrac{11}{38}$ in die Gleichung der Lotgeraden ein.

$\vec X_{M'}=\begin{pmatrix}2\\4\\5\end{pmatrix}-\dfrac{11}{38}\cdot\begin{pmatrix}1\\6\\1\end{pmatrix}=\begin{pmatrix}2-\dfrac{11}{38}\\[2ex]4-\dfrac{66}{38}\\[2ex]5-\dfrac{11}{38}\end{pmatrix}=\begin{pmatrix}\dfrac{65}{38}\\[2ex]\dfrac{43}{19}\\[2ex]\dfrac{179}{38}\end{pmatrix}$

Antwort: Der Mittelpunkt $M'$ hat die Koordinaten $M'\left(\dfrac{65}{38}\big\vert\dfrac{43}{19}\big\vert\dfrac{179}{38}\right)$ .

Berechnung des Schnittkreisradius $r'$

Kugel K1 mit Schnittebene, Mittelpunkt M' und r'

In der Abbildung ist nur die Kugel $K_1$ dargestellt.

Den Schnittkreisradius $r'$ kannst du mithilfe des Satzes von Pythagoras berechnen. Der Abstand $d$ der Ebene $E$ vom Mittelpunkt $M_1$ ist der Betrag des Vektors $\overrightarrow{M_1M'}$ und der Kugelradius von $K_1$ ist $r=3$ .

Berechne zuerst den Vektor $\overrightarrow{M_1M'}$ und dann dessen Betrag.

$\overrightarrow{M_1M'}=\begin{pmatrix}\dfrac{65}{38}\\[2ex]\dfrac{43}{19}\\[2ex]\dfrac{179}{38}\end{pmatrix}-\begin{pmatrix}2\\4\\5\end{pmatrix}=\begin{pmatrix}-\dfrac{11}{38}\\[2ex]-\dfrac{33}{19}\\[2ex]-\dfrac{11}{38}\end{pmatrix}$

$d=\Big\vert\overrightarrow{M_1M'}\Big\vert=\sqrt{\left(-\dfrac{11}{38}\right)^2+\left(-\dfrac{33}{19}\right)^2+\left(-\dfrac{11}{38}\right)^2}=\sqrt{\dfrac{121}{38}}\approx1{,}78$

$\displaystyle r^2$	$=$	$\displaystyle d^2+r'^2$
	↓	Nach $r'$ auflösen.
$\displaystyle r'$	$=$	$\displaystyle \sqrt{r^2-d^2}$
	↓	Setze $r=3$ und $d=\sqrt{\dfrac{121}{38}}$ ein.
	$=$	$\displaystyle \sqrt{3^2-\left(\sqrt{\dfrac{121}{38}}\right)^2}$
	↓	Berechne die Quadrate.
	$=$	$\displaystyle \sqrt{9-\dfrac{121}{38}}$
	↓	Vereinfache.
	$=$	$\displaystyle \sqrt{\dfrac{221}{38}}$
	$≈$	$\displaystyle 2{,}41$

Antwort: Der Radius $r'$ des Schnittkreises beträgt $\sqrt{\dfrac{221}{38}}\approx 2{,}41\; \text{LE}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Gegeben sind die Kugeln $K_1: \left(\vec x-\begin{pmatrix}7\\-2\\0\end{pmatrix}\right)^2=4$ und $K_2: \left(\vec x-\begin{pmatrix}7\\1\\4\end{pmatrix}\right)^2=9$

Zeige, dass sich die beiden Kugeln außen in einem Punkt $B$ berühren und gib seine Koordinaten an. Bestimme auch die Tangentialebene $E_T$ der beiden Kugeln.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentialebene

Kugeln berühren sich

Berechne den Vektor $\overrightarrow{M_1M_2}$ und dann seinen Betrag $d(M_1M_2)=\Big\vert \overrightarrow{M_1M_2}\Big\vert$ .

$\overrightarrow{M_1M_2}=\begin{pmatrix}7\\1\\4\end{pmatrix}-\begin{pmatrix}7\\-2\\0\end{pmatrix}=\begin{pmatrix}0\\3\\4\end{pmatrix}$

$d(M_1M_2)=\Big\vert \overrightarrow{M_1M_2}\Big\vert=\sqrt{0^2+3^2+4^2}=\sqrt{25}=5$

$r_1=\sqrt{4}=2$ und $r_2=\sqrt{9}=3\;\;\Rightarrow\; r_1+r_2=2+3=5$

Der Abstand der beiden Kugelmittelpunkte beträgt $5$ und die Summe der beiden Kugelradien beträgt auch $5$ .

$d(M_1M_2)=r_1+r_2=5\;\; \Rightarrow\;\;$ Die beiden Kugeln berühren sich außen.

Berechnung von $B$

Aus der nebenstehenden Abbildung kannst du folgende Vektorgleichung ablesen:

$\overrightarrow{OB}=\overrightarrow{OM_1}+r_1\cdot\vec{n}_0$

Dabei ist

$\vec{n}_0=\dfrac{\overrightarrow{M_1M_2}}{\Big\vert\overrightarrow{M_1M_2}\Big\vert}$

$\overrightarrow{OB}=\overrightarrow{OM_1}+r_1\cdot\vec{n}_0=\overrightarrow{OM_1}+r_1\cdot\dfrac{\overrightarrow{M_1M_2}}{\Big\vert\overrightarrow{M_1M_2}\Big\vert}$

Dabei ist $r_1=2$ , $\Big\vert \overrightarrow{M_1M_2}\Big\vert=5$ und $\vec n_0=\dfrac{1}{5}\cdot\begin{pmatrix}0\\3\\4\end{pmatrix}$ .

$\overrightarrow{OB}=\begin{pmatrix}7\\-2\\0\end{pmatrix}+2\cdot\dfrac{1}{5}\cdot\begin{pmatrix}0\\3\\4\end{pmatrix}=\begin{pmatrix}7+0\\[2ex]-2+\dfrac{6}{5}\\[2ex]0+\dfrac{8}{5}\end{pmatrix}=\begin{pmatrix}7\\[2ex]-\dfrac{4}{5}\\[2ex]\dfrac{8}{5}\end{pmatrix}$

Antwort: Der Berührpunkt hat die Koordinaten $B\left(7\Big\vert -\dfrac{4}{5}\Big\vert \dfrac{8}{5}\right)$ .

Berechnung von $E_T$

Mit Hilfe des berechneten Einheitsvektors $\vec n_0$ und einem Punkt der Ebene (hier der Berührpunkt $B$ ) kann die Gleichung der Tangentialebene erstellt werden. Bei Verwendung von $\vec n_0$ erhältst du die Hessesche Normalenform der Ebene bzw. nach Berechnung des Skalarproduktes eine Koordinatenform.

$\displaystyle E:\;(\vec x-\vec p)\circ \vec n_0$	$=$	$\displaystyle 0$
	↓	Setze $B$ und $\vec n_0$ ein.
$\displaystyle \left(\vec x-\begin{pmatrix}7\\[2ex]-\dfrac{4}{5}\\[2ex]\dfrac{8}{5}\end{pmatrix}\right)\circ \dfrac{1}{5}\cdot\begin{pmatrix}0\\3\\4\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Das ist die Hessesche Normalenform der Tangentialebene.
$\displaystyle \left(\begin{pmatrix}x_1\\[2ex]x_2\\[2ex]x_3\end{pmatrix}-\begin{pmatrix}7\\[2ex]-\dfrac{4}{5}\\[2ex]\dfrac{8}{5}\end{pmatrix}\right)\circ \dfrac{1}{5}\cdot\begin{pmatrix}0\\3\\4\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Umwandlung in die Koordinatenform.
$\displaystyle \begin{pmatrix}x_1-7\\[2ex]x_2+\dfrac{4}{5}\\[2ex]x_3-\dfrac{8}{5}\end{pmatrix}\circ \dfrac{1}{5}\cdot\begin{pmatrix}0\\3\\4\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Berechne das Skalarprodukt.
$\displaystyle \dfrac{1}{5}\cdot\left((x_1-7)\cdot0+(x_2+\dfrac{4}{5})\cdot3+(x_3-\dfrac{8}{5})\cdot4\right)$	$=$	$\displaystyle 0$
	↓	Löse die Klammern auf.
$\displaystyle \dfrac{1}{5}\cdot\left(0+3x_2+\dfrac{12}{5}+4x_3-\dfrac{32}{5}\right))$	$=$	$\displaystyle 0$
	↓	Vereinfache.
$\displaystyle \dfrac{1}{5}\cdot\left(3x_2+4x_3-\dfrac{20}{5}\right))$	$=$	$\displaystyle 0$
	↓	Vereinfache.
$\displaystyle \dfrac{1}{5}\cdot\left(3x_2+4x_3-4\right))$	$=$	$\displaystyle 0$

Antwort: Die Hessesche Koordinatenform der Tangentialebene $E_T$ lautet: $\dfrac{1}{5}\cdot(3x_2+4x_3-4)=0$ bzw. Tangentialebene $E_T$ als Koordinatengleichung: $3x_2+4x_3=4$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Gegeben sind die Kugeln $K_1: \left(\vec x-\begin{pmatrix}8\\1\\5\end{pmatrix}\right)^2=1600$ und

$K_2: \left(\vec x-\begin{pmatrix}3\\1\\-7\end{pmatrix}\right)^2=729$

Zeige, dass sich die beiden Kugeln innen in einem Punkt $B$ berühren und gib seine Koordinaten an. Bestimme auch die Tangentialebene $E_T$ der beiden Kugeln.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentialebene

Kugeln berühren sich

Berechne den Vektor $\overrightarrow{M_1M_2}$ und dann seinen Betrag $d(M_1M_2)=\Big\vert \overrightarrow{M_1M_2}\Big\vert$ .

$\overrightarrow{M_1M_2}=\begin{pmatrix}3\\1\\-7\end{pmatrix}-\begin{pmatrix}8\\1\\5\end{pmatrix}=\begin{pmatrix}-5\\0\\-12\end{pmatrix}$

$d(M_1M_2)=\Big\vert \overrightarrow{M_1M_2}\Big\vert=\sqrt{(-5)^2+0^2+(-12)^2}=\sqrt{169}=13$

$r_1=\sqrt{1600}=40$ und $r_2=\sqrt{729}=27\;\;\Rightarrow\; |r_1-r_2|=|40-27|=13$

Der Abstand der beiden Kugelmittelpunkte beträgt $13$ und die Differenz der beiden Kugelradien beträgt auch $13$ .

$d(M_1M_2)=|r_1-r_2|=13\;\; \Rightarrow\;\;$ Die beiden Kugeln berühren sich innen.

Berechnung von $B$

Aus der nebenstehenden Abbildung kannst du folgende Vektorgleichung ablesen:

$\overrightarrow{OB}=\overrightarrow{OM_1}+r_1\cdot\vec{n}_0$

Dabei ist

$\vec{n}_0=\dfrac{\overrightarrow{M_1M_2}}{\Big\vert\overrightarrow{M_1M_2}\Big\vert}$

$\overrightarrow{OB}=\overrightarrow{OM_1}+r_1\cdot\vec{n}_0=\overrightarrow{OM_1}+r_1\cdot\dfrac{\overrightarrow{M_1M_2}}{\Big\vert\overrightarrow{M_1M_2}\Big\vert}$

Dabei ist $r_1=40$ , $\Big\vert \overrightarrow{M_1M_2}\Big\vert=13$ und $\vec n_0=\dfrac{1}{13}\cdot\begin{pmatrix}-5\\0\\-12\end{pmatrix}$ .

$\overrightarrow{OB}=\begin{pmatrix}8\\1\\5\end{pmatrix}+40\cdot\dfrac{1}{13}\cdot\begin{pmatrix}-5\\0\\-12\end{pmatrix}=\begin{pmatrix}8-\dfrac{200}{13}\\[2ex]1+0\\[2ex]5-\dfrac{480}{13}\end{pmatrix}=\begin{pmatrix}-\dfrac{96}{13}\\[2ex]1\\[2ex]-\dfrac{415}{13}\end{pmatrix}$

Antwort: Der Berührpunkt hat die Koordinaten $B\left(-\dfrac{96}{13}\Big\vert 1\Big\vert -\dfrac{415}{13}\right)$ .

Berechnung von $E_T$

Mit dem eben berechneten Einheitsvektor $\vec n_0=\dfrac{1}{13}\cdot\begin{pmatrix}-5\\0\\-12\end{pmatrix}$ und dem Berührpunkt $B\left(-\dfrac{96}{13}\Big\vert 1\Big\vert -\dfrac{415}{13}\right)$ , der ein Punkt der Ebene $E_T$ ist, kann die Gleichung der Tangentialebene erstellt werden.

Hinweis: Bei Verwendung des Einheitsvektors erhält man die Hessesche Normalenform der Ebene bzw. nach Berechnung des Skalarproduktes eine Koordinatenform.

$\displaystyle (\vec{x}-\vec{b})\circ\vec{n}_0$	$=$	$\displaystyle 0$
	↓	Setze $B$ und $\vec{n}_0$ ein.
$\displaystyle E_T:\;\left(\vec x-\begin{pmatrix}-\dfrac{96}{13}\\[2ex]1\\[2ex]-\dfrac{415}{13}\end{pmatrix}\right)\circ \dfrac{1}{13}\cdot\begin{pmatrix}-5\\[2ex]0\\[2ex]-12\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Das ist die Hessesche Normalenform der Ebene.
$\displaystyle \begin{pmatrix}x_1+\dfrac{96}{13}\\[2ex]x_2-1\\[2ex]x_3+\dfrac{415}{13}\end{pmatrix}\circ \dfrac{1}{13}\cdot\begin{pmatrix}-5\\[2ex]0\\[2ex]-12\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Für die Umwandlung in die Koordinatenform berechne das Skalarprodukt.
$\displaystyle \dfrac{1}{13}\cdot((x_1+\dfrac{96}{13})\cdot(-5)+(x_2-1)\cdot 0+(x_3+\dfrac{415}{13})\cdot(-12))$	$=$	$\displaystyle 0$
	↓	Löse die Klammern auf.
$\displaystyle \dfrac{1}{13}\cdot(-5x_1-\dfrac{480}{13}+0-12x_3-\dfrac{4980}{13})$	$=$	$\displaystyle 0$
	↓	Fasse zusammen.
$\displaystyle \dfrac{1}{13}\cdot(-5x_1-12x_3-\dfrac{5460}{13})$	$=$	$\displaystyle 0$
	↓	Vereinfache.
$\displaystyle \dfrac{1}{13}\cdot(-5x_1-12x_3-420)$	$=$	$\displaystyle 0$

Antwort: Die Hessesche Koordinatenform der Tangentialebene $E_T$ lautet: $\dfrac{1}{13}\cdot(-5x_1-12x_3-420)=0$ oder nur als Koordinatenform $E_T:\;5x_1+12x_3=-420$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

4
Welche Kugeln um den Mittelpunkt $M_2(6|7|9)$ berühren die Kugel
$K_1:\;\left(\vec x-\begin{pmatrix}4 \\ 4 \\ 3 \end{pmatrix}\right)^2=9$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenseitige Lage von zwei Kugeln
Bei dieser Aufgabe gibt es zwei mögliche Lösungen.
Die beiden Kugeln können sich außen berühren (Fall 1) oder sie können sich innen berühren (Fall 2).
Fall 1: Bei einem äußeren Berührpunkt muss der Abstand der beiden Kugelmittelpunkte $d(M_1M_2)=\Big\vert\overrightarrow{M_1M_2}\Big\vert$ gleich der Summe der beiden Kugelradien sein: $d(M_1M_2)=r_1+r_2$
Berechne zunächst den Vektor $\overrightarrow{M_1M_2}$ und dann seinen Betrag.
$\overrightarrow{M_1M_2}=\overrightarrow{OM_2}-\overrightarrow{OM_1}=\begin{pmatrix} 6 \\ 7 \\9 \end{pmatrix}-\begin{pmatrix} 4 \\ 4 \\ 3 \end{pmatrix}=\begin{pmatrix} 2 \\3 \\ 6 \end{pmatrix}$
$d(M_1M_2)=\Big\vert\overrightarrow{M_1M_2}\Big\vert=\sqrt{2^2+3^2+6^2}=\sqrt{49}=7$
Gegeben ist der Kugelradius: $r_1=\sqrt{9}=3$ gesucht ist $r_2$ .
$d(M_1M_2)=r_1+r_2\;\;\Rightarrow\;r_2=d(M_1M_2)-r_1=7-3=4$
Antwort: Die Kugel $K_2$ hat einen Radius von $r_2=4$ und die Kugelgleichung lautet: $K_2:\;\left(\vec x-\begin{pmatrix}6 \\ 7 \\ 9 \end{pmatrix}\right)^2=4^2=16$
Fall 2: Bei einem inneren Berührpunkt muss der Abstand der beiden Kugelmittelpunkte $d(M_1M_2)=\Big\vert\overrightarrow{M_1M_2}\Big\vert$ gleich dem Betrag der Differenz der beiden Kugelradien sein: $d(M_1M_2)=|r_1-r_2|$
Der Abstand der beiden Kugelmittelpunkte $d(M_1M_2)=\Big\vert\overrightarrow{M_1M_2}\Big\vert=7$ wurde schon beim Fall 1 berechnet. Es muss also $d(M_1M_2)=|r_1-r_2|=7$ sein.
Der Radius $r_1=3\;\;\Rightarrow\;|3-r_2|=7$
Fall +
$3-r_2=7\;\;\Rightarrow\;r_2=-4$ ; Diese Lösung entfällt wegen $r>0$ .
Fall -
$-3+r_2=7\;\;\Rightarrow\;r_2=10$
Antwort: Die Kugel $K_2$ hat einen Radius von $r_2=10$ und die Kugelgleichung lautet: $K_2:\;\left(\vec x-\begin{pmatrix}6 \\ 7 \\ 9 \end{pmatrix}\right)^2=10^2=100$
Die beiden Kugeln $\left(\vec x-\begin{pmatrix}6 \\ 7 \\ 9 \end{pmatrix}\right)^2=16$ und $\left(\vec x-\begin{pmatrix}6 \\ 7 \\ 9 \end{pmatrix}\right)^2=100$ berühren die Kugel $K_1:\;\left(\vec x-\begin{pmatrix}4 \\ 4 \\ 3 \end{pmatrix}\right)^2=9$ .
5
Zwei Kugeln berühren sich außen in Punkt $B(1|-1|1)$ . Die Kugelradien sind $r_1=2$ und $r_2=4$ . Die Verbindungsgerade der beiden Kugelmittelpunkte $M_1$ und $M_2$ hat den Richtungsvektor $\vec v_{M_1M_2}=\begin{pmatrix}-1\\2\\-2\end{pmatrix}$ . Bestimme die Kugelgleichungen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zwei Kugeln mit gemeinsamen äußeren Berührpunkt
Die beiden sich außen berührenden Kugeln können auf zwei verschiedene Arten angeordnet sein.
Fall 1: Die größere Kugel liegt rechts von der kleineren Kugel.
Fall 2: Die größere Kugel liegt links von der kleineren Kugel.
Lösung für den Fall 1
Die Berechnung der beiden Kugelmittelpunkte erfolgt mit Hilfe einer Vektorgleichung.
Der Abbildung kannst du folgende Vektorgleichungen entnehmen.
$\mathrm{(I)}:\;\overrightarrow{OM_2}=\overrightarrow{OB}+\overrightarrow{BM_2}$ und $\mathrm{(II)}:\;\overrightarrow{OM_1}=\overrightarrow{OB}+\overrightarrow{BM_1}$
Dabei ist der Vektor $\overrightarrow{OB}=\begin{pmatrix}1\\-1\\1\end{pmatrix}$ gegeben. Die beiden Vektoren $\overrightarrow{BM_2}$ bzw. $\overrightarrow{BM_1}$ müssen berechnet werden.
Berechnung von $\overrightarrow{BM_2}$ für Kugel $K_2$
Aus dem gegebenen Richtungsvektor $\vec v_{M_1M_2}=\begin{pmatrix}-1\\2\\-2\end{pmatrix}$ erstellst du einen Einheitsvektor $\vec n_0=\dfrac{\vec v_{M_1M_2}}{|\vec v_{M_1M_2}|}$ . Dazu muss der Betrag von $\vec v_{M_1M_2}$ berechnet werden:
$|\vec v_{M_1M_2}|=\sqrt{(-1)^2+2^2+(-2)^2}=\sqrt{9}=3\;\Rightarrow\;\vec n_0=\dfrac{1}{3}\cdot \begin{pmatrix}-1\\2\\-2\end{pmatrix}$
Für den Vektor $\overrightarrow{BM_2}$ gilt mit dem berechneten Einheitsvektor $\vec n_0$ und $r_2=4$ :
$\overrightarrow{BM_2}=r_2 \cdot \vec n_0=4\cdot\dfrac{1}{3}\cdot \begin{pmatrix}-1\\2\\-2\end{pmatrix}=\dfrac{4}{3}\cdot \begin{pmatrix}-1\\2\\-2\end{pmatrix}$
Berechnung von $\overrightarrow{OM_2}$
$\overrightarrow{OM_2}=\overrightarrow{OB}+\overrightarrow{BM_2}$
$\overrightarrow{OM_2}=\begin{pmatrix}1\\-1\\1\end{pmatrix}+\dfrac{4}{3}\cdot \begin{pmatrix}-1\\2\\-2\end{pmatrix}=\begin{pmatrix}1-\dfrac{4}{3}\\[2ex]-1+\dfrac{8}{3}\\[2ex]1-\dfrac{8}{3}\end{pmatrix}=\begin{pmatrix}-\dfrac{1}{3}\\[2ex]\dfrac{5}{3}\\[2ex]-\dfrac{5}{3}\end{pmatrix}$
Der Mittelpunkt der Kugel $K_2$ hat die Koordinaten:
$M_2\left(-\dfrac{1}{3}\Big\vert\dfrac{5}{3}\Big\vert-\dfrac{5}{3}\right)$ .
Berechnung von $\overrightarrow{BM_1}$ für Kugel $K_1$
Für den Vektor $\overrightarrow{BM_1}$ gilt mit dem oben berechneten Einheitsvektor $(-\vec n_0)$ und $r_1=2$ :
$\overrightarrow{BM_1}=r_1 \cdot (-\vec n_0)=2\cdot\dfrac{1}{3}\cdot \begin{pmatrix}1\\-2\\2\end{pmatrix}=\dfrac{2}{3}\cdot \begin{pmatrix}1\\-2\\2\end{pmatrix}$
Berechnung von $\overrightarrow{OM_1}$
$\overrightarrow{OM_1}=\overrightarrow{OB}+\overrightarrow{BM_1}$
$\overrightarrow{OM_1}=\begin{pmatrix}1\\-1\\1\end{pmatrix}+\dfrac{2}{3}\cdot \begin{pmatrix}1\\-2\\2\end{pmatrix}=\begin{pmatrix}1+\dfrac{2}{3}\\[2ex]-1-\dfrac{4}{3}\\[2ex]1+\dfrac{4}{3}\end{pmatrix}=\begin{pmatrix}\dfrac{5}{3}\\[2ex]-\dfrac{7}{3}\\[2ex]\dfrac{7}{3}\end{pmatrix}$
Der Mittelpunkt der Kugel $K_1$ hat die Koordinaten:
$M_1\left(\dfrac{5}{3}\Big\vert-\dfrac{7}{3}\Big\vert\dfrac{7}{3}\right)$ .
Antwort: Damit können die beiden Kugelgleichungen angegeben werden:
$K_1:\; \left(\vec x-\begin{pmatrix}\dfrac{5}{3}\\[2ex]-\dfrac{7}{3}\\[2ex]\dfrac{7}{3}\end{pmatrix}\right)^2=2^2=4$ und
$K_2:\; \left(\vec x-\begin{pmatrix}-\dfrac{1}{3}\\[2ex]\dfrac{5}{3}\\[2ex]-\dfrac{5}{3}\end{pmatrix}\right)^2=4^2=16$
Lösung für den Fall 2
Der Abbildung kannst du folgende Vektorgleichungen entnehmen.
$\mathrm{(I)}:\;\overrightarrow{OM_2'}=\overrightarrow{OB}+\overrightarrow{BM_2'}$ und $\mathrm{(II)}:\;\overrightarrow{OM_1'}=\overrightarrow{OB}+\overrightarrow{BM_1'}$
Dabei ist der Vektor $\overrightarrow{OB}=\begin{pmatrix}1\\-1\\1\end{pmatrix}$ gegeben. Die beiden Vektoren $\overrightarrow{BM_2'}$ bzw. $\overrightarrow{BM_1'}$ müssen berechnet werden.
Berechnung von $\overrightarrow{BM_2'}$ für Kugel $K_2$
Für den Vektor $\overrightarrow{BM_2'}$ gilt mit dem oben berechneten Einheitsvektor $(-\vec n_0)$ und $r_2=4$ :
$\overrightarrow{BM_2'}=r_2 \cdot(-\vec n_0)=4\cdot\dfrac{1}{3}\cdot \begin{pmatrix}1\\-2\\2\end{pmatrix}=\dfrac{4}{3}\cdot \begin{pmatrix}1\\-2\\2\end{pmatrix}$
Berechnung von $\overrightarrow{OM_2'}$
$\overrightarrow{OM_2'}=\overrightarrow{OB}+\overrightarrow{BM_2'}$
$\overrightarrow{OM_2'}=\begin{pmatrix}1\\-1\\1\end{pmatrix}+\dfrac{4}{3}\cdot \begin{pmatrix}1\\-2\\2\end{pmatrix}=\begin{pmatrix}1+\dfrac{4}{3}\\[2ex]-1-\dfrac{8}{3}\\[2ex]1+\dfrac{8}{3}\end{pmatrix}=\begin{pmatrix}\dfrac{7}{3}\\[2ex]-\dfrac{11}{3}\\[2ex]\dfrac{11}{3}\end{pmatrix}$
Der Mittelpunkt der Kugel $K_2$ hat die Koordinaten:
$M_2'\left(\dfrac{7}{3}\Big\vert-\dfrac{11}{3}\Big\vert\dfrac{11}{3}\right)$ .
Berechnung von $\overrightarrow{BM_1'}$ für Kugel $K_1$
Für den Vektor $\overrightarrow{BM_1'}$ gilt mit dem oben berechneten Einheitsvektor $\vec n_0$ und $r_1=2$ :
$\overrightarrow{BM_1'}=r_1 \cdot \vec n_0=2\cdot\dfrac{1}{3}\cdot \begin{pmatrix}-1\\2\\-2\end{pmatrix}=\dfrac{2}{3}\cdot \begin{pmatrix}-1\\2\\-2\end{pmatrix}$
Berechnung von $\overrightarrow{OM_1'}$
$\overrightarrow{OM_1'}=\overrightarrow{OB}+\overrightarrow{BM_1'}$
$\overrightarrow{OM_1}=\begin{pmatrix}1\\-1\\1\end{pmatrix}+\dfrac{2}{3}\cdot \begin{pmatrix}-1\\2\\-2\end{pmatrix}=\begin{pmatrix}1-\dfrac{2}{3}\\[2ex]-1+\dfrac{4}{3}\\[2ex]1-\dfrac{4}{3}\end{pmatrix}=\begin{pmatrix}\dfrac{1}{3}\\[2ex]\dfrac{1}{3}\\[2ex]-\dfrac{1}{3}\end{pmatrix}$
Der Mittelpunkt der Kugel $K_1$ hat die Koordinaten:
$M_1\left(\dfrac{1}{3}\Big\vert\dfrac{1}{3}\Big\vert-\dfrac{1}{3}\right)$ .
Antwort: Damit können die beiden Kugelgleichungen angegeben werden
$K_1':\; \left(\vec x-\begin{pmatrix}\dfrac{1}{3}\\[2ex]\dfrac{1}{3}\\[2ex]-\dfrac{1}{3}\end{pmatrix}\right)^2=2^2=4$ und
$K_2':\; \left(\vec x-\begin{pmatrix}\dfrac{7}{3}\\[2ex]-\dfrac{11}{3}\\[2ex]\dfrac{11}{3}\end{pmatrix}\right)^2=4^2=16$
Die beiden sich außen berührenden Kugeln können auf zwei verschiedene Arten angeordnet werden, d.h. es gibt insgesamt vier Kugelgleichungen zu bestimmen.
Die Berechnung der beiden Kugelmittelpunkte erfolgt mit Hilfe einer Vektorgleichung.
$\mathrm{(I)}:\;\overrightarrow{OM_2}=\overrightarrow{OB}+\overrightarrow{BM_2}$ und $\mathrm{(II)}:\;\overrightarrow{OM_1}=\overrightarrow{OB}+\overrightarrow{BM_1}$
Dabei ist der Vektor $\overrightarrow{OB}$ gegeben und die beiden Vektoren $\overrightarrow{BM_2}$ bzw. $\overrightarrow{BM_1}$ müssen berechnet werden.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben mit zwei Kugeln

Lagebeziehung der beiden Kugeln

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichungen

Kugel K1K_1K1​:

Kugel K2K_2K2​:

Schnitt der beiden Kugeln berechnen

Hast du eine Frage oder Feedback?

Berechnung des Mittelpunkt M′M'M′

Berechnung des Schnittkreisradius r′r'r′

Hast du eine Frage oder Feedback?

Mittelpunkt M′M'M′

Schnittkreisradius r′r'r′

Kugeln berühren sich

Berechnung von BBB

Berechnung von ETE_TET​

Kugeln berühren sich

Berechnung von BBB

Berechnung von ETE_TET​

Lösung für den Fall 1

Berechnung von BM2→\overrightarrow{BM_2}BM2​​ für Kugel K2K_2K2​

Berechnung von OM2→\overrightarrow{OM_2}OM2​​

Berechnung von BM1→\overrightarrow{BM_1}BM1​​ für Kugel K1K_1K1​

Berechnung von OM1→\overrightarrow{OM_1}OM1​​

Lösung für den Fall 2

Berechnung von BM2′→\overrightarrow{BM_2'}BM2′​​ für Kugel K2K_2K2​

Berechnung von OM2′→\overrightarrow{OM_2'}OM2′​​

Berechnung von BM1′→\overrightarrow{BM_1'}BM1′​​ für Kugel K1K_1K1​

Berechnung von OM1′→\overrightarrow{OM_1'}OM1′​​

Kugel $K_1$ :

Kugel $K_2$ :

Berechnung des Mittelpunkt $M'$

Berechnung des Schnittkreisradius $r'$

Mittelpunkt $M'$

Schnittkreisradius $r'$

Berechnung von $B$

Berechnung von $E_T$

Berechnung von $B$

Berechnung von $E_T$

Berechnung von $\overrightarrow{BM_2}$ für Kugel $K_2$

Berechnung von $\overrightarrow{OM_2}$

Berechnung von $\overrightarrow{BM_1}$ für Kugel $K_1$

Berechnung von $\overrightarrow{OM_1}$

Berechnung von $\overrightarrow{BM_2'}$ für Kugel $K_2$

Berechnung von $\overrightarrow{OM_2'}$

Berechnung von $\overrightarrow{BM_1'}$ für Kugel $K_1$

Berechnung von $\overrightarrow{OM_1'}$