Prüfungsaufgaben Mathematik 2022
🎓 Prüfungsbereich für Berlin
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Formelsammlung, die der Prüfung beiliegt.
- 1
Basisaufgaben (10 Punkte)
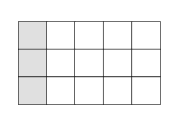
Markieren Sie der nebenstehenden Fläche. (1P)

Auf dem Markt kosten Äpfel
Geben Sie den Preis für Äpfel an. (1P)
Gegeben ist die Gleichung .
Kreuzen Sie an, welche Zahl die Lösung der Gleichung ist. (1P)
In der dargestellten Woche waren es im Durchschnitt .
Ergänzen Sie die fehlende Temperatur. (1P)
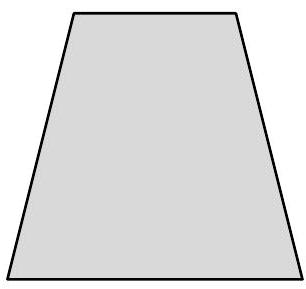
Geben Sie eine Gleichung zur Berechnung des Flächeninhalts des Dreiecks an. (1P)
Jeder fünfte Jugendliche bekommt kein Taschengeld.
Kreuzen Sie an, wie viel Prozent das sind. (1P)
Kreuzen Sie an, welche Aussage in einem rechtwinkligen Dreieck gilt. (1P)
Max trinkt am Tag 1,5 Liter Wasser. Er benutzt ein Glas.
Geben Sie an, wie viele volle Gläser Wasser das sind. (1P)
Diese Figur ist ein gleichschenkliges Trapez.
Kreuzen Sie an, wie viele Symmetrieachsen die Figur hat. (1P)
Setzen Sie das richtige Zeichen ein. (1P)
- 2
Becher (11 Punkte)
Gegeben ist ein zylinderförmiger Becher ohne Deckel. Die Höhe beträgt und der Radius .
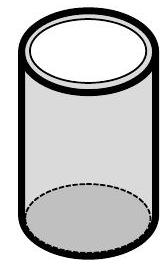
(Skizze nicht maßstabsgerecht)
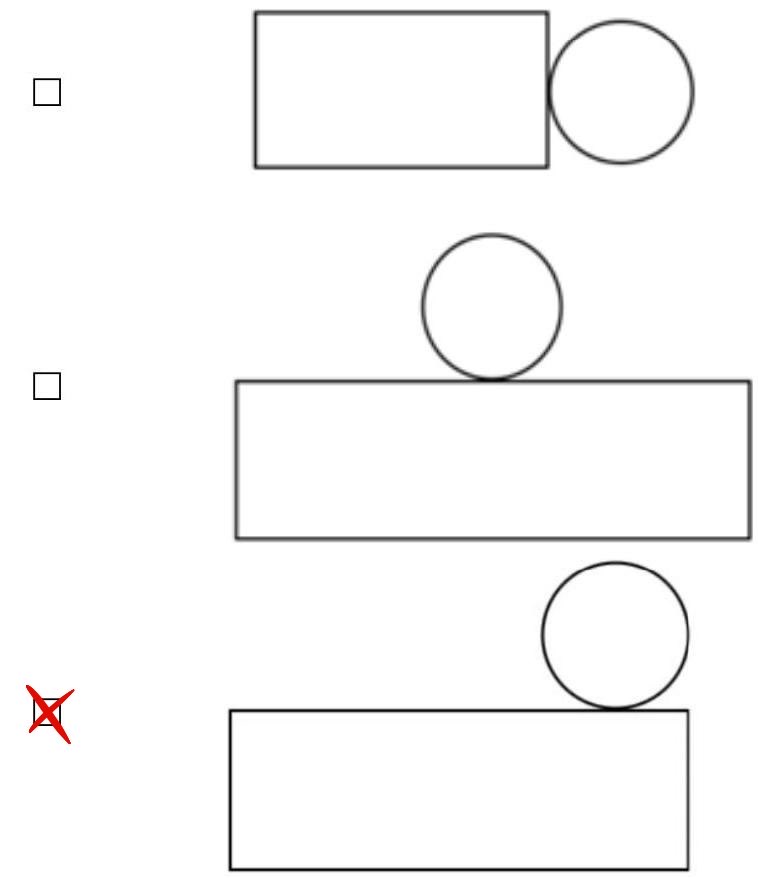
Wählen Sie aus den vorgegebenen Skizzen das Netz aus, das zum Becher passt. Kreuzen Sie an.
Ermitteln Sie die Länge und die Breite der Mantelfläche.
(3P)
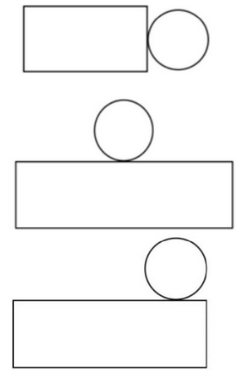
Zeigen Sie, dass in den Becher Flüssigkeit passen.
Hinweis: entspricht (2P)
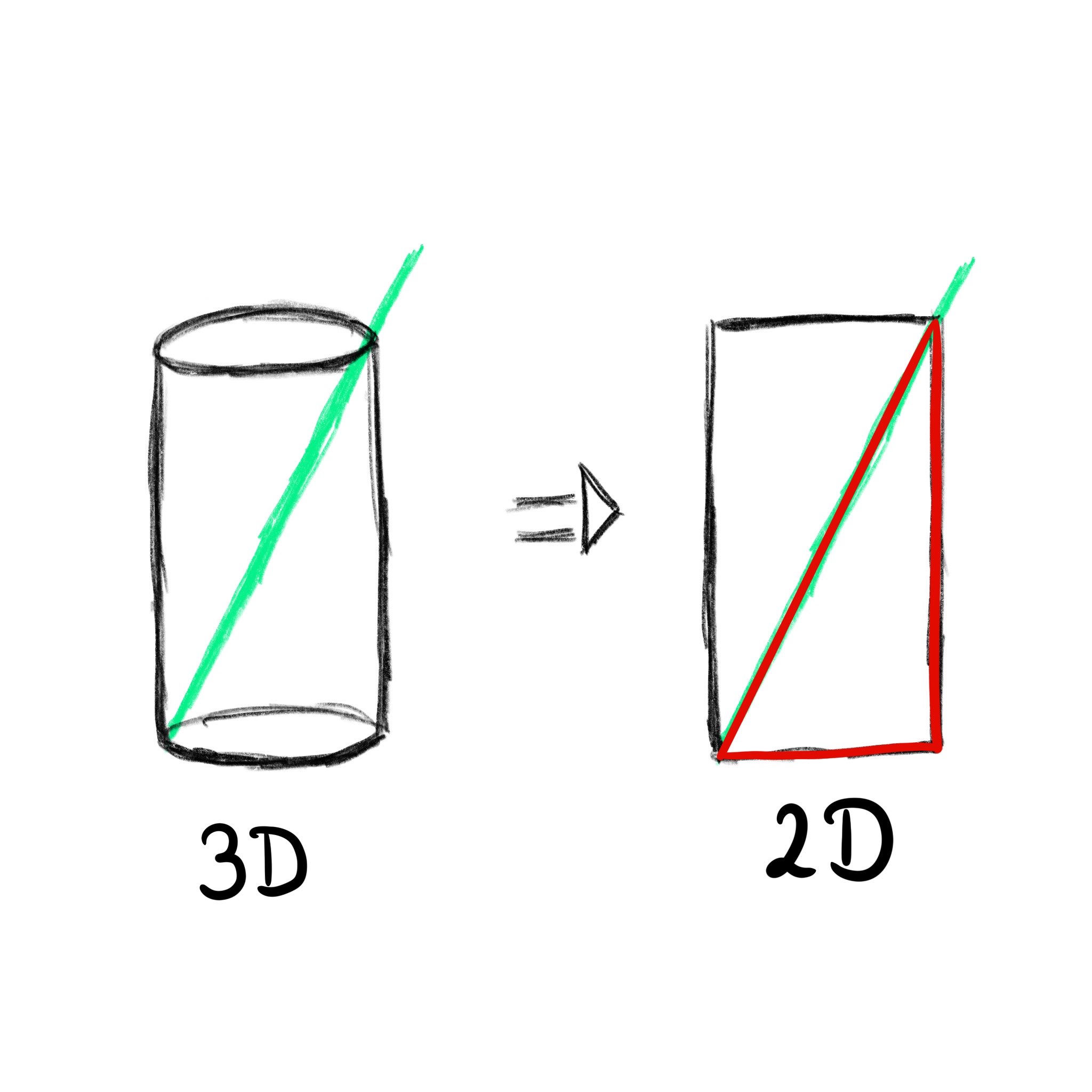
Ein Stab wird zum Umrühren genutzt. Von dem Stab sind außerhalb des Bechers, wenn er diagonal im Becher steht (siehe Skizze).
Bestimmen Sie die Länge des Stabes. (3P)
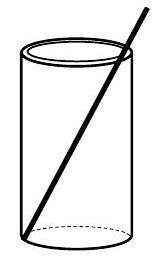
(Skizze nicht maßstabsgerecht)
Ein größerer Becher soll ein Volumen von haben.
Die Höhe von wird beibehalten.
Berechnen Sie den Radius dieses Bechers. (3P)
- 3
Funktionen (8 Punkte)
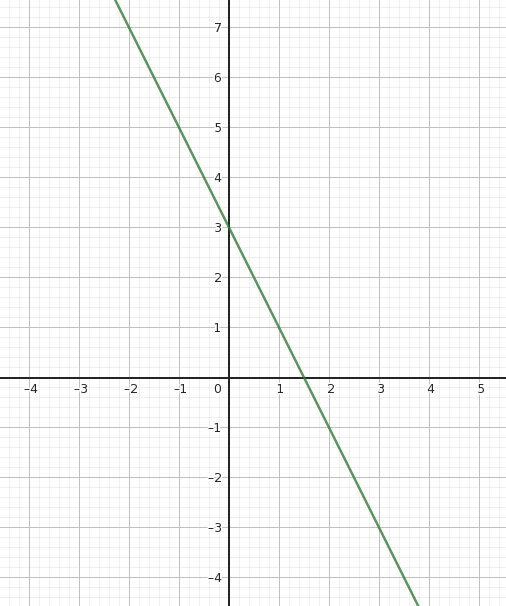
Gegeben ist eine lineare Funktion mit der Gleichung .
Zeichnen Sie den Graphen der gegebenen linearen Funktion in das Koordinatensystem.
Geben Sie die Nullstelle der Funktion an. (3P)
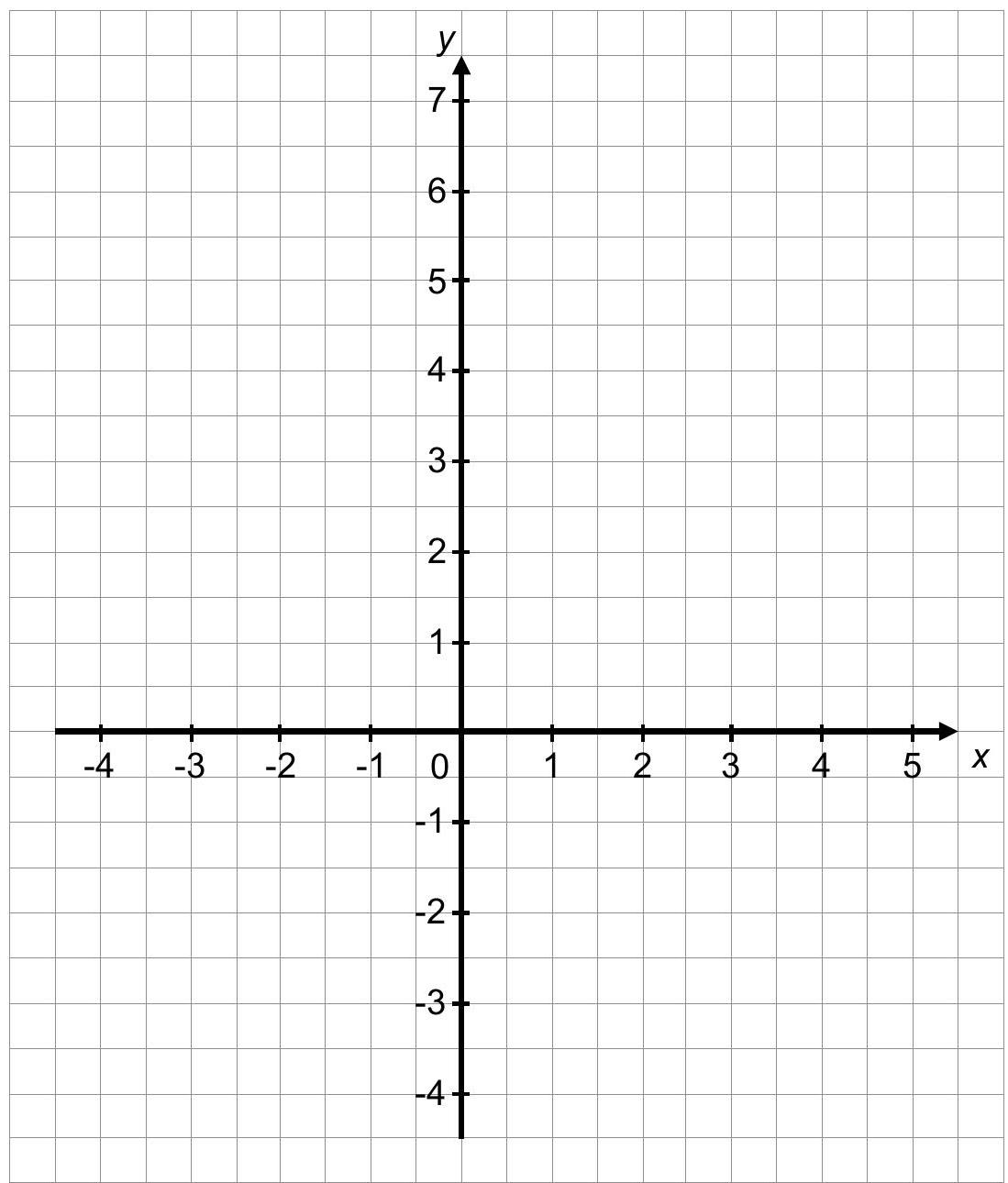
Gegeben ist die Funktionsgleichung einer verschobenen Normalparabel .
Geben Sie die Koordinaten des Scheitelpunktes an. (1P)
Ermitteln Sie die Koordinaten der Schnittpunkte der Geraden mit der Parabel . (4P)
- 4
Bücher (10 Punkte)
In den Jahren 2017 bis 2021 wurden jeweils 1200 Jugendliche in Deutschland befragt, wie oft sie Bücher lesen.
Das Diagramm zeigt, wie viele der Befragten mehrmals pro Woche Bücher lesen.
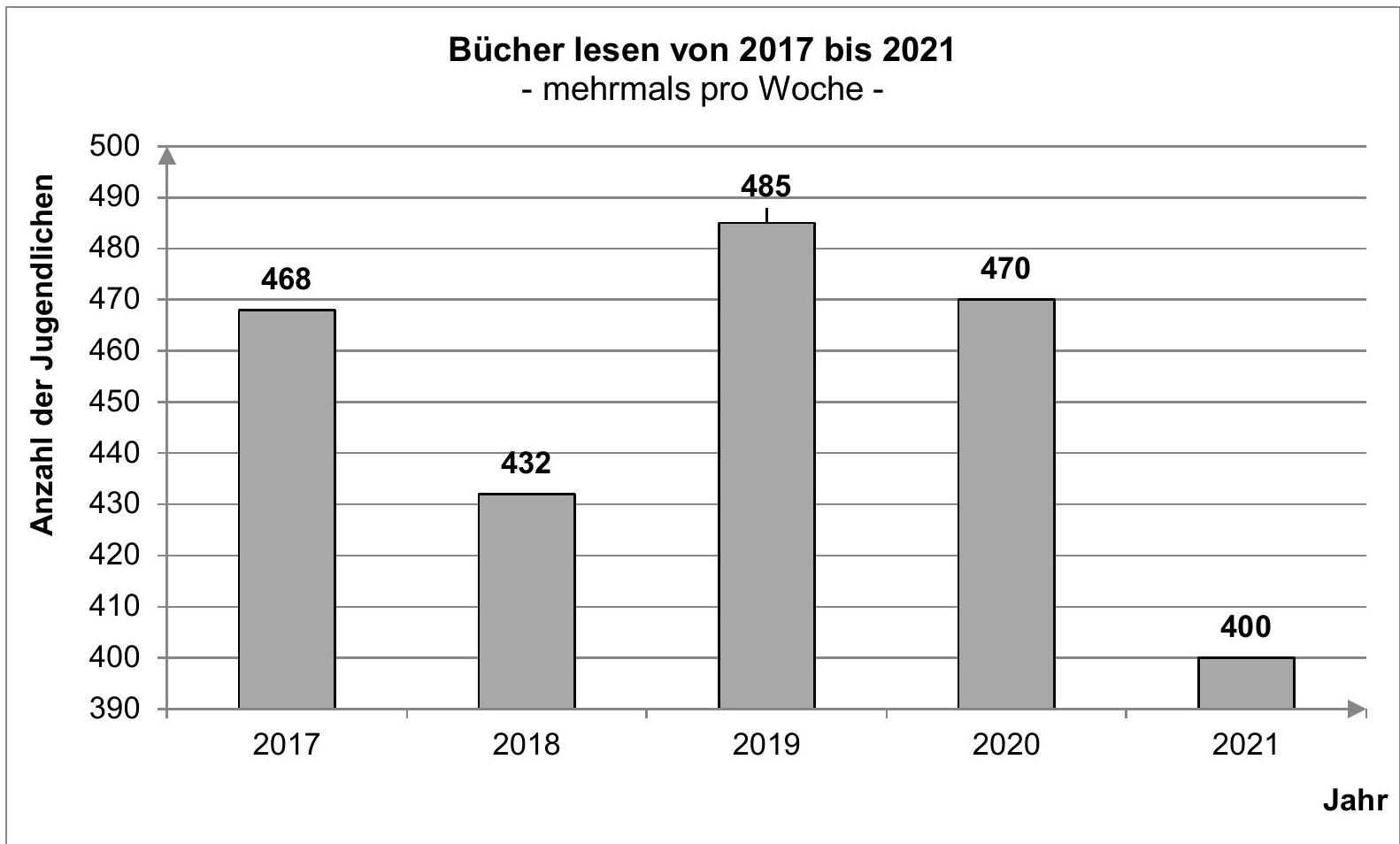
Geben Sie das Minimum und das Maximum der Anzahl der Jugendlichen an, die mehrmals pro Woche Bücher lesen.
Bestimmen Sie die durchschnittliche Anzahl (das arithmetische Mittel) der Jugendlichen, die mehrmals pro Woche Bücher lesen. (3P)
Ermitteln Sie, um wie viel Prozent die Anzahl der Jugendlichen im Diagramm von 2020 bis 2021 gesunken ist. (2P)
Paolo sieht auf das Diagramm und behauptet:
„Von Jahr zu Jahr lesen immer weniger Jugendliche Bücher. Von 2018 bis 2021 hat sich die Anzahl der bücherlesenden Jugendlichen um mehr als die Hälfte reduziert.“
Entscheiden Sie, ob Paolos Aussage wahr ist.
Begründen Sie Ihre Entscheidung. (2P)
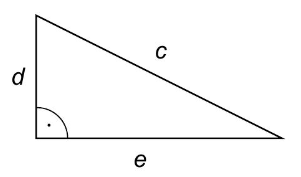
750 Jugendliche wurden befragt, wie häufig sie Comic-Hefte lesen.
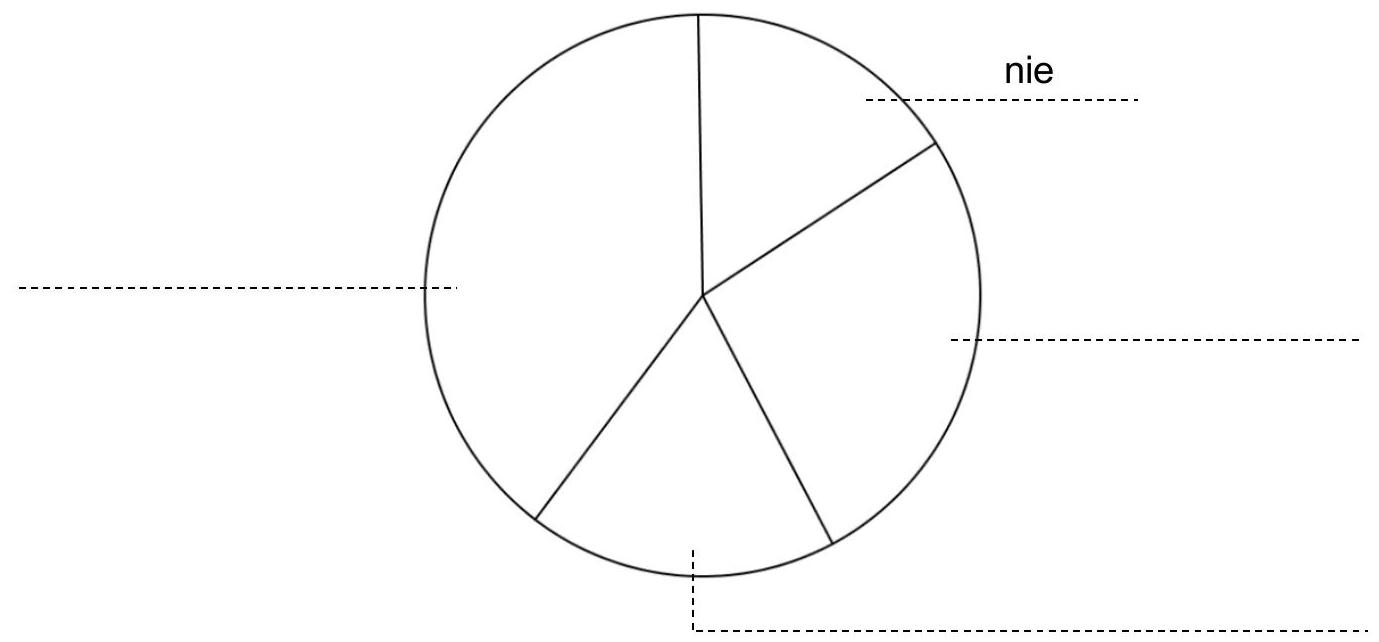
Die folgende Tabelle zeigt die prozentuale Verteilung.
mehrmals pro Woche
einmal pro Woche
einmal im Monat
nie
Beschriften Sie das Kreisdiagramm entsprechend der Tabelle. (3P)
- 5
Dreiecke (11 Punkte)
Gegeben ist ein Dreieck
Das Dreieck ist nicht rechtwinklig.
Die Höhe beträgt ca. .
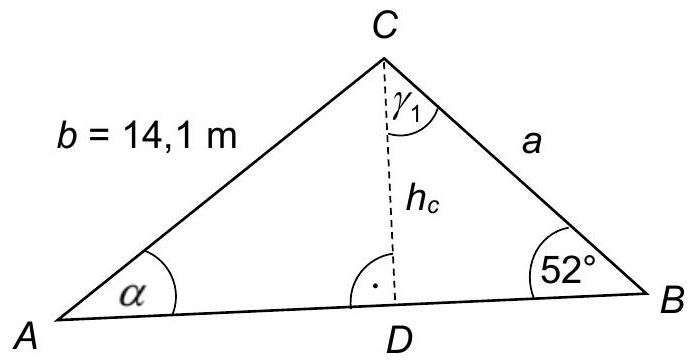
(Skizze nicht maßstabsgerecht)
Weisen Sie nach, dass die Länge der Strecke ca. beträgt. (2P)
Berechnen Sie die Größe des Winkels . (2P)
Ermitteln Sie die Größe des Winkels . (2P)
Berechnen Sie die Länge der Seite . (2P)
Ermitteln Sie den Flächeninhalt des Dreiecks . (3P)
- 6
Führerschein (5 Punkte)
Zu ihrem 16. Geburtstag haben Maxi und Paula Geld geschenkt bekommen. Sie sparen monatlich weiter, damit sie die Fahrschule für ihren Führerschein bezahlen können.

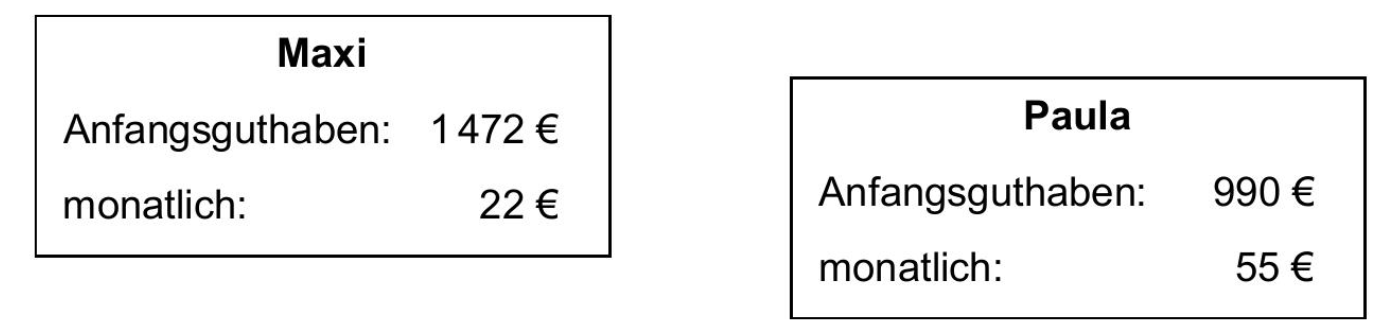
Paula hat nach einem Jahr in der Spardose.
Berechnen Sie, wie viel Euro Maxi nach einem Jahr in der Spardose hat. (1P)
Stellen Sie eine Gleichung auf, mit der Paulas Gesamtguthaben berechnet werden kann.
y: Gesamtguthaben in
: Anzahl der Monate
Für die Fahrschule und die Führerscheinprüfung benötigt Paula .
Ermitteln Sie, wie viele Monate Paula mindestens sparen muss, um ihr Ziel zu erreichen.
(4P)
- 7
Bäume (5 Punkte)
Frau Bauer kauft für ihren Garten Apfelbäume und Pflaumenbäume.
Ein Apfelbaum und ein Pflaumenbaum kosten zusammen 63,00
Für 9 Apfelbäume und 3 Pflaumenbäume zahlt sie .
Frau Bauer stellt folgende zwei Gleichungen zum Sachverhalt auf:
I
II

Geben Sie die Bedeutung der Variablen und an. (2P)
Berechnen Sie den Preis für einen Apfelbaum und den Preis für einen Pflaumenbaum. (3P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?