1 Übersicht
Inhalt des Kurses
In diesem Kurs wird die Matrixmultiplikation wiederholt und die Drehung von Punkten und Geraden um einen Punkt in der Ebene erklärt. Außerdem werden besondere Drehwinkel genauer betrachtet.
Vorkenntnisse
Du solltest Vektoren im Zweidimensionalen verstanden haben.
Dazu gehört auch Vektoren zwischen zwei Punkten aufstellen und Vektoren addieren und subtrahieren. Zum Wiederholen kannst du dir die 2 Kurse Vektoren in der Ebene I und Vektoren in der Ebene II anschauen.
Kursdauer
1,5 Stunden
2 Die Matrix
Definition
Eine Matrix ist eine rechteckige Anordnung von mathematischen Objekten. Sie hat im Allgemeinen Zeilen und Spalten, also: Einträge. Die Pluralform heißt Matrizen.
Beispiele von Matrizen
2x2 Matrix
Allgemein:
konkret:
3x3 Matrix
Allgemein:
konkret:
3 Erklärung: Multiplikation einer 2x2 Matrix mit einem Vektor
Merkspruch: Zeile mal Spalte
Im folgenden Applet kann man sich nochmal alles Schritt für Schritt ansehen:
4 Beispiel: Multiplikation einer 2x2 Matrix mit einem Vektor
Merkspruch: Zeile mal Spalte
Man verwendet die Formel
Daher muss man den ersten Eintrag der ersten Zeile der Matrix mit dem oberen Eintrag des Vektors multiplizieren und den zweiten Eintrag der ersten Zeile der Matrix mit dem unteren Eintrag des Vektors multiplizieren. Die Summe der beiden Produkte ist der obere Eintrag der Lösung.
Um nun den unteren Eintrag deiner Lösung zu erhalten, muss man dasselbe für die zweite Zeile wiederholen.
Also wird der erste Eintrag der zweiten Zeile der Matrix mit dem oberen Eintrag des Vektors multipliziert und der zweite Eintrag der zweiten Zeile der Matrix mit dem unteren Eintrag des Vektors multipliziert. Die Summe der beiden Produkte ergibt den unteren Eintrag der Lösung.
5 Aufgaben: Multiplikation einer 2x2 Matrix mit einem Vektor
Jetzt bist du dran.
Laden
6 Herleitung der Abbildungsgleichung (1/2)
Der Punkt wird mit dem Winkel um den Ursprung gedreht.
Welche Koordinaten hat jetzt der neue Punkt ?
Um diese Frage beantworten zu können, benötigt man die Abbildungsgleichung der Drehung. Diese wird im folgenden hergeleitet:
Zuerst bestimmt man die Koordinaten des Hilfspunktes , der durch Drehung des grünen Dreiecks entsteht:
da rechtwinkliges Dreieck mit Hypotenuse
da rechtwinkliges Dreieck mit Hypotenuse
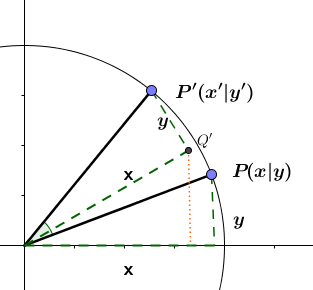
Um die Koordinaten von zu berechnen, läuft man zuerst vom Ursprung zum Hilfspunkt und dann weiter zu . Man bildet also eine Vektorkette:
Den Vektor erhält man mit Hilfe der Polarkoordinaten:
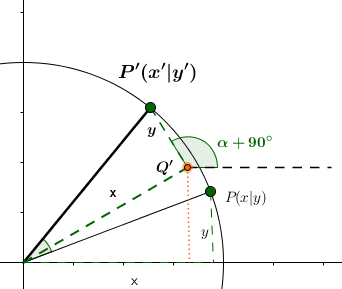
7 Herleitung der Abbildungsgleichung (2/2)
Zur Wiederholung:
Jetzt wendet man die Additionstheoreme an, um dies zu vereinfachen.
Der Punkt hat also folgende Koordinaten:
Nun schreibt man das noch in der Matrixschreibweise, um den Ausgangsvektor als auch den Bildvektor hervorzuheben:
8 Beispiel: Drehung eines Punktes um den Ursprung
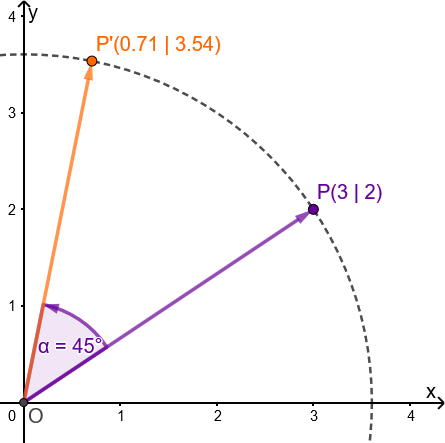
Drehung des Punktes um .
Man wendet nun die Matrixformel an, die man gerade hergeleitet bzw. gelernt hat:
Jetzt wird der Winkel und der Punkt eingesetzt.
Der Bildpunkt besitzt also die Koordinaten .
9 Aufgaben: Drehung eines Punktes um den Ursprung
Jetzt bist du dran.
Laden
10 Beispiel: Drehung einer Geraden um den Ursprung
Die Gerade mit soll mit dem Winkel um den Ursprung gedreht werden.
Gesucht ist jetzt also die Geradengleichung von .
Man wählt einen allgemeinen Punkt auf der Geraden und dreht diesen um um den Ursprung:
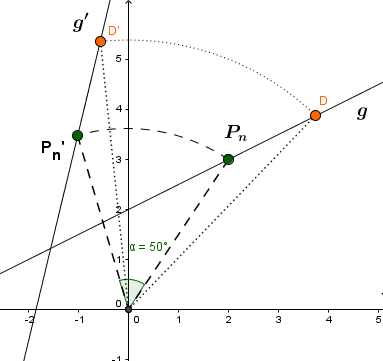
Nun haben wir einen Punkt erhalten, der auf der Bildgeraden liegt.
Gesucht ist aber die Gleichung der Geraden . Diese ist der Trägergraph der Punkte .
Dazu löst man die Gleichung nach auf.
Diese Gleichung setzt man nun in ein:
Die gedrehte Gerade besitzt also etwa die Gleichung .
11 Aufgaben: Drehung einer Geraden um den Ursprung
Jetzt bist du dran.
Laden
12 Drehung mit besonderen Winkelmaßen
Da Drehungen mit Winkelmaßen wie und besonders häufig vorkommen, sollte man sich für die speziellen Winkelmaße die Abbildungsgleichungen gut einprägen.
Drehung um | Koordinatenform | Matrixform |
|---|---|---|
Punktspiegelung | ||
13 Drehung eines Punktes um einen beliebigen Punkt Z
Der Punkt soll um das Zentrum mit dem Winkel gedreht werden.
Um diese Abbildung zu beschreiben, definiert man sich einen Hilfspunkt mit folgender Bedingung:
Nun wird der Hilfspunkt mit dem Winkel um den Ursprung gedreht:
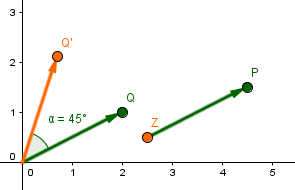
Im letzten Schritt muss man an den Vektor den Vektor anhängen und erhält somit :
Also zusammenfassend kann gesagt werden:
Man dreht zuerst den Vektor um den Ursprung und führt im Anschluss eine Parallelverschiebung mit dem Vektor durch:
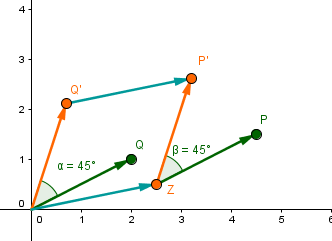
14 Beispiel: Drehung eines Punktes um einen beliebigen Punkt Z
Der Punkt soll um das Zentrum mit dem Winkel gedreht werden.
Wie in der Herleitung dreht man zuerst den Vektor
um den Ursprung:
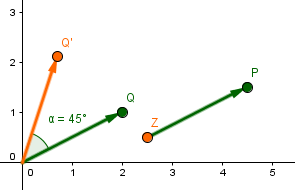
Jetzt muss nur noch die Parallelverschiebung durchgeführt werden:
Der Punkt besitzt also die Koordinaten .
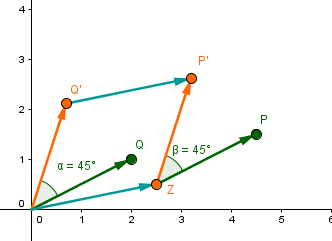
15 Aufgaben: Drehung eines Punktes um einen beliebigen Punkt Z
Jetzt bist du dran.
Laden
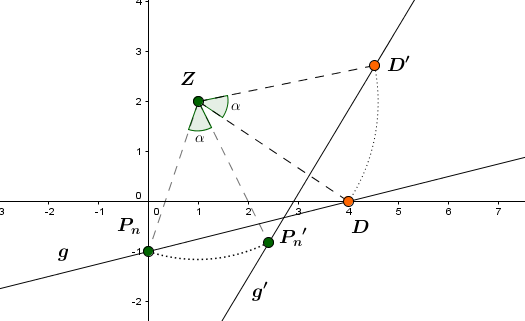
16 Beispiel: Drehung einer Gerade g um einen beliebigen Punkt Z
Die Gerade mit soll mit dem Winkel um das Zentrum gedreht werden.
Gesucht ist jetzt also die Geradengleichung von .
Man wählt einen allgemeinen Punkt auf der Geraden und dreht diesen um um :
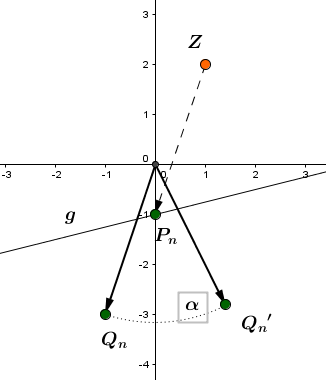
1. Drehung des Vektors um den Ursprung:
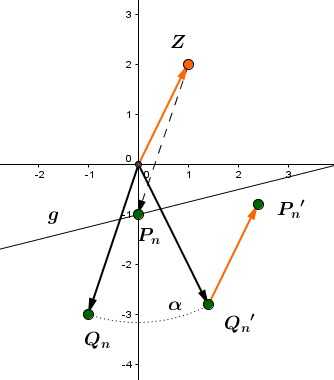
2. Parallelverschiebung
Jetzt muss nur noch die Parallelverschiebung durchgeführt werden:
3. Berechnung des Trägergraphs
Als erstes löst man die (1)-Gleichung nach auf.
Das wird nun in (2) eingesetzt:
Die gedrehte Gerade hat demnach folgende Gleichung
17 Aufgaben: Drehung einer Geraden g um einen beliebigen Punkt Z
Jetzt bist du dran!
Laden
18 Zusammenfassung und Ausblicke
Hier nocheinmal eine Zusammenfassung des in diesem Kurs behandelten Stoffes:
Drehung um den Ursprung
in Koordinatenform:
in Matrixform:
Drehung von Punkt um einen beliebigen Punkt
in Matrixform:
Zugehörige Themen
Artikel: Verknüpfung von Abbildungen
weitere Aufgaben und Artikel zum Thema: Abbildungen im Koordinatensystem
