Gemischte Aufgaben zu linearen Funktionen

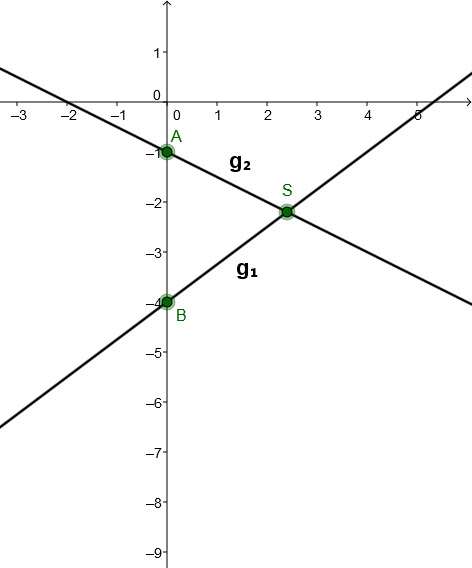
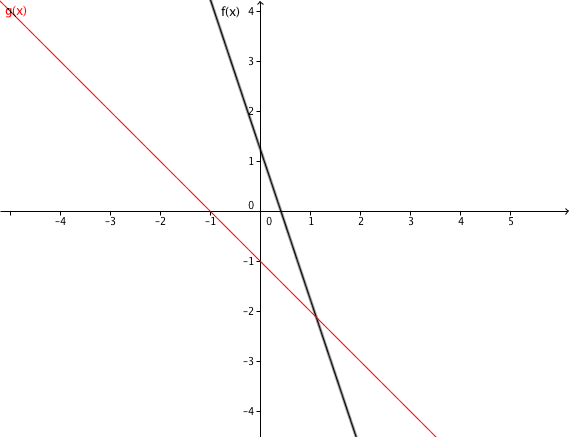
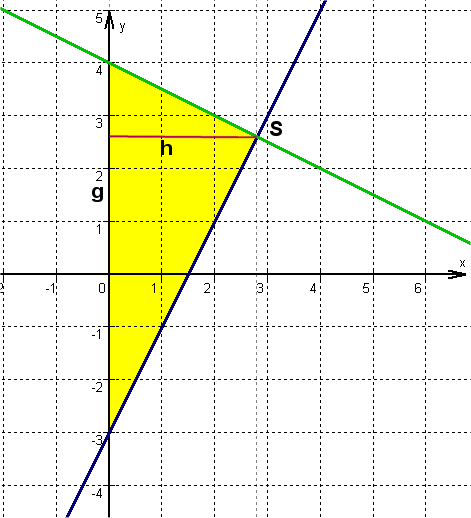
1

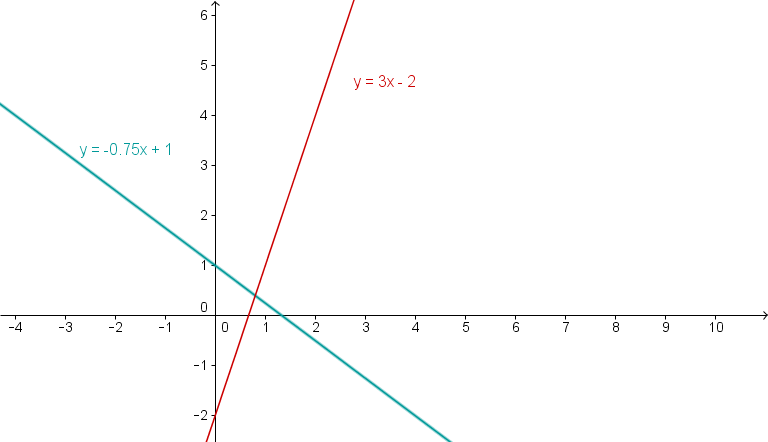
Zeichne die Geraden $\mathrm y=3\mathrm x-2$ und $\mathrm y=-\frac34\mathrm x+1$ in ein Koordinatensystem. Bestimme die Nullstellen und den Schnittpunkt der Geraden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen

Zeichne die Graphen

Geogebra File: https://assets.serlo.org/legacy/4905_6fWpNpSnfx.xml

Bestimmung der Nullstellen

$\mathrm y=3\mathrm x-2$

Setze y=0 um die Nullstelle zu bestimmen. Denn an der Stelle, an der y=0, schneidet die Gerade die x-Achse.

$\displaystyle 3x-2$	$=$	$\displaystyle 0$	$\displaystyle +2$
$\displaystyle 3x$	$=$	$\displaystyle 2$	$\displaystyle :3$
$\displaystyle \mathrm{x}_{\mathrm{N1}}$	$=$	$\displaystyle \frac{2}{3}$
	↓	Die erste Gerade hat bei $\mathrm{x}_{\mathrm{N}}=\frac{2}{3}$ eine Nullstelle.

Gehe für die zweite Gerade genauso vor.

$\displaystyle y$	$=$	$\displaystyle -\frac{3}{4}\mathrm{x}+1$
	↓	Setze y=0 um die Nullstelle zu bestimmen.
$\displaystyle -\frac{3}{4}\mathrm{x}+1$	$=$	$\displaystyle 0$	$\displaystyle -1$
$\displaystyle -\frac{3}{4}x$	$=$	$\displaystyle -1$	$\displaystyle :\left(-\frac{3}{4}\right)$
$\displaystyle x$	$=$	$\displaystyle \frac{1}{\frac{3}{4}}$
	↓	Du dividierst durch einen Bruch $\rightarrow$ Multipliziere mit dem Kehrwert
$\displaystyle \mathrm{x}_{\mathrm{N2}}$	$=$	$\displaystyle \frac{4}{3}$
	↓	Die zweite Gerade hat bei $\mathrm x_\mathrm N=\frac43$ eine Nullstelle.

Bestimmung des Schnittpunkts

Setze die beiden Funktionsgleichungen gleich. Die Geraden schneiden sich dort, wo beide an der gleichen x-Stelle denselben y-Wert haben.

$\displaystyle 3\mathrm{x}-2$	$=$	$\displaystyle -\frac{3}{4}\mathrm{x}+1$	$\displaystyle +\frac{3}{4}x\ +2$
$\displaystyle 3\mathrm{x}+\frac{3}{4}\mathrm{x}$	$=$	$\displaystyle 1+2$
$\displaystyle 3{,}75x$	$=$	$\displaystyle 3$	$\displaystyle :3{,}75$
$\displaystyle x$	$=$	$\displaystyle \frac{3}{3{,}75}$
$\displaystyle \mathrm{x}_{\mathrm{S}}$	$=$	$\displaystyle 0{,}8$
	↓	Setze $x_S$ in eine der beiden Funktionen ein.
$\displaystyle y$	$=$	$\displaystyle 3\cdot0{,}8-2$
$\displaystyle y$	$=$	$\displaystyle 2{,}4-2$
$\displaystyle \mathrm{y}_{\mathrm{S}}$	$=$	$\displaystyle 0{,}4$

$\;\;\Rightarrow\;\;S\left(0{,}8\vert0{,}4\right)$

Der Schnittpunkt liegt bei $S\left(0{,}8\vert0{,}4\right)$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

2

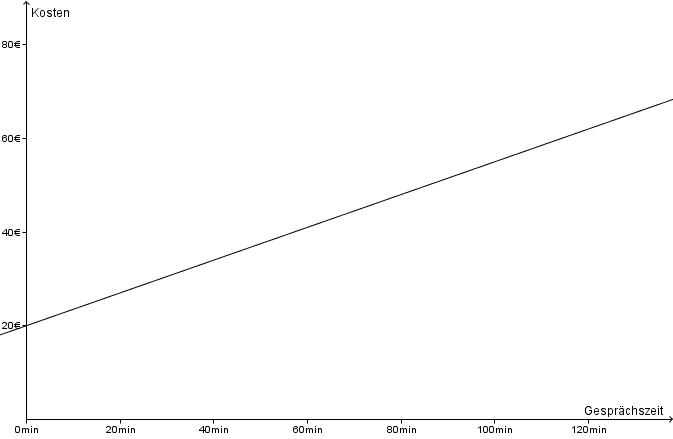
Herr Breuer hat einen Handyvertrag mit folgenden Konditionen abgeschlossen:

Monatliche Grundgebühr 20€, Telefonkosten pro Minute 0,35€.

Wie hoch ist seine Monatsrechnung, wenn er 40, 80 oder 120 Minuten telefoniert?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Grundgebühr: 20€
Kosten pro Minute: 0,35€
Monatsrechnung ist Grundgebühr plus Kosten für telefonierte Minuten.
Monatsrechnung bei 40 Minuten
Herr Breuer hat 40 Minuten telefoniert.
Berechne die Kosten für diese 40 Minuten.
$40\cdot 0{,}35€=14€$
Fasse zur Monatsrechnung zusammen.
Gesamtkosten = $20€+14€=34€$
Herr Breuer zahlt 34€ wenn er 40 Minuten telefoniert.
Monatsrechnung bei 80 Minuten
Herr Breuer hat 80 Minuten telefoniert.
Berechne die Kosten für diese 80 Minuten.
$80\cdot 0{,}35€=28€$
Fasse zur Monatsrechnung zusammen.
Gesamtkosten = $20€+28€=48€$
Herr Breuer zahlt 48€ wenn er 80 Minuten telefoniert.
Monatsrechnung bei 120 Minuten
Herr Breuer hat 120 Minuten telefoniert.
Berechne die Kosten für diese 120 Minuten.
$120\cdot 0{,}35€=42€$
Fasse zur Monatsrechnung zusammen.
Gesamtkosten = $20€+42€=62€$
Herr Breuer zahlt 62€ wenn er 120 Minuten telefoniert.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle einen Term für die monatlichen Kosten in Abhängigkeit von der Gesprächsdauer in Minuten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Monatliche Kosten = Grundgebühr + Kosten für telefonierte Minuten.
Sei $x$ Anzahl der telefonierten Minuten.
Berechne damit die Kosten.
Kosten = $20€+0{,}35€\cdot x$
Drücke das als lineare Funktion aus.
$f(x)=0{,}35\cdot x+20$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle den Zusammenhang graphisch dar.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
$f(x)=0{,}35x+20$
Diese Funktion hat den y-Achsenabschnitt $20$ , schneidet die $y$ -Achse also in $(0|20)$ . Ihre Steigung ist $0{,}35$ . Zeichne also einen Punkt bei z.B. $(10\;|\;20+10\cdot0{,}35)=(10\,|\,23{,}5)$ . Verbinde diese Punkte zur gesuchten Geraden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

3

Ein Lieferwagen, der mit 1,2 t beladen ist, transportiert x Stücke zu je $25\;kg$ und y Kisten zu je $150\;kg$ .

Stelle den Zusammenhang zwischen x und y in einem Diagramm dar.
Welche Punkte $\left(x;\;y\right)$ sind möglich, wenn der Lieferwagen maximal 1,2 t beladen ist?

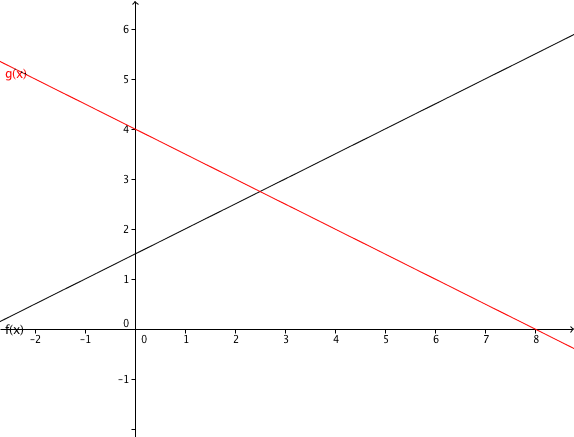
4

Betrachte folgende Graphen.

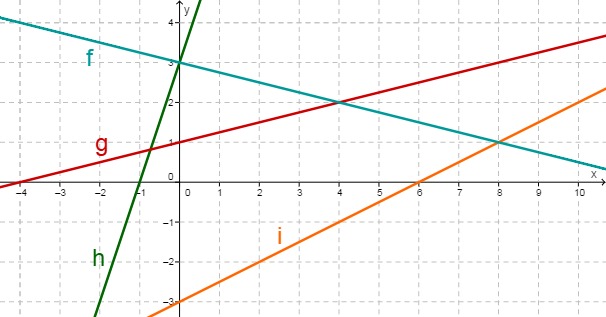
Bestimme die Funktionsgleichungen von allen 4 Geraden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
$\text f(x):y=m_fx+b_f$
Um die Geradengleichung von f zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden f liegen. In diesem Fall ergibt sich zum Beispiel $A(0|3)$ und $B(4|2)$ . Bestimme mit diesen die Steigung von f mit der Formel.
$\displaystyle m_f=\frac{y_B-y_A}{x_B-x_A}$
Setz die Werte ein.
$\displaystyle m_f=\frac{2-3}{4-0}=-\frac14$
Bestimme jetzt den y-Achsenabschnitt $b_f$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf f liegt, oder abliest, bei welchem Wert f die y-Achse schneidet.
$\text f(x):y=m_fx+b_f$
Setz zum Beispiel $A$ ein.
$\displaystyle 3=-\frac14\cdot0+b_f$
Vereinfache.
$3=b_f\Rightarrow b_f=3$
Also lautet die Geradengleichung $\displaystyle\text f(x)=-\frac14\cdot x+3$ .
$\text g(x):y=m_gx+b_g$
Um die Geradengleichung von g zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden g liegen. In diesem Fall ergibt sich zum Beispiel $C(-4|0)$ und $D(0|1)$ . Bestimme mit diesen die Steigung von g mit der Formel.
$\displaystyle m_g=\frac{y_D-y_C}{x_D-x_C}$
Setz die Werte ein.
$\displaystyle m_g=\frac{1-0}{0-(-4)}=\frac14$
Bestimme jetzt den y-Achsenabschnitt $b_g$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf g liegt, oder abliest, bei welchem Wert g die y-Achse schneidet.
$\text g(x):y=m_gx+b_g$
Setz zum Beispiel $D$ ein.
$\displaystyle 1=\frac14\cdot0+b_g$
Vereinfache.
$\displaystyle 1=b_g\Rightarrow b_g=1$
Also lautet die Geradengleichung $\displaystyle\text g(x)=\frac14\cdot x+1$ .
$\text h(x):y=m_hx+b_h$
Um die Geradengleichung von h zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden h liegen. In diesem Fall ergibt sich zum Beispiel $E(-1|0)$ und $A(0|3)$ . Bestimme mit diesen die Steigung von h mit der Formel.
$\displaystyle m_h=\frac{y_A-y_E}{x_A-x_E}$
Setz die Werte ein.
$\displaystyle m_h=\frac{3-0}{0-(-1)}=3$
Bestimme jetzt den y-Achsenabschnitt $b_h$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf h liegt, oder abliest, bei welchem Wert h die y-Achse schneidet.
$\text h(x):y=m_hx+b_h$
Setz zum Beispiel $A$ ein.
$3=3\cdot0+b_h$
Vereinfache.
$3=b_h\Rightarrow b_h=3$
Also lautet die Geradengleichung $\displaystyle\text h(x)=3\cdot x+3$ .
$\text i(x):y=m_ix+b_i$
Um die Geradengleichung von i zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden i liegen. In diesem Fall ergibt sich zum Beispiel $F(0|-3)$ und $S(6|0)$ . Bestimme mit diesen die Steigung von i mit der Formel.
$\displaystyle m_i=\frac{y_S-y_F}{x_S-x_F}$
Setz die Werte ein.
$\displaystyle m_i=\frac{0-(-3)}{6-0}=\frac12$
Bestimme jetzt den y-Achsenabschnitt $b_i$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf i liegt, oder abliest, bei welchem Wert i die y-Achse schneidet.
$\text i(x):y=m_ix+b_i$
Setz zum Beispiel $F$ ein.
$\displaystyle-3=\frac12\cdot0+b_i$
Vereinfache.
$-3=b_i\Rightarrow b_i=-3$
Also lautet die Geradengleichung $\displaystyle\text i(x)=\frac12\cdot x-3$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme den Schnittpunkt von g und h , sowie die Nullstelle von f.

Berechne die beiden Schnittpunkte, die außerhalbdes Bildbereichs liegen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen

Der Schnittpunkt von h und i und der Schnittpunkt von g und i liegen außerhalb des Bildbereichs.

Schnittpunkt $T(x_T|y_T)$ von h und i

Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach $x$ um. Die Funktionsgleichungen lauten (Teilaufgabe a) $h(x):y=3x+3$ und $\displaystyle i(x):y=\frac12x-3$ .

$\displaystyle \displaystyle3x_T+3$	$=$	$\displaystyle \frac12x_T-3$	$\displaystyle -\frac{1}{2}x-3$
$\displaystyle \frac{5}{2}x_T$	$=$	$\displaystyle -6$	$\displaystyle :\frac{5}{2}$
$\displaystyle x_T$	$=$	$\displaystyle -\frac{12}{5}$

Setz nun $-\frac{12}{5}$ in die Geradengleichung von h oder i ein, um $y_T$ zu bestimmen.

$h(x_T):y_T=3⋅x_T+3$

Setz $x_T$ ein.

$\displaystyle y_T=3\cdot\left(-\frac{12}5\right)+3=-\frac{21}5$

Die Geraden h und i schneiden sich also bei $\displaystyle T\left(-\frac{12}5\left|-\frac{21}5\right.\right)$ .

Schnittpunkt $Q(x_Q|y_Q)$ von g und i

Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach $x$ um. Die Funktionsgleichungen lauten (Teilaufgabe a) $\displaystyle g(x):y=\frac14x+1$ und $\displaystyle i(x):y=\frac12x-3$ .

$\displaystyle \displaystyle\frac14x_Q+1$	$=$	$\displaystyle \frac12x_Q-3$	$\displaystyle -\frac{1}{2}x-1$
$\displaystyle \displaystyle -\frac14x_Q$	$=$	$\displaystyle -4$	$\displaystyle :\left(-\frac{1}{4}\right)$

$\displaystyle x_Q=16$

Setz nun $16$ in die Geradengleichung von g oder i ein, um $y_Q$ zu bestimmen.

$\displaystyle g(x_Q):y_Q=\frac14⋅x_Q+1$

Setz $x_Q$ ein.

$\displaystyle y_Q=\frac14\cdot16+1=5$

Die Geraden g und i schneiden sich also bei $\displaystyle Q(16|5)$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Wie viele Schnittpunkte gibt es höchstens bei vier Geraden, die jeweils nicht parallel sind?
Schnittpunkte kann es höchstens geben.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Es gibt insgesamt 6 Schnittpunkte, nämlich die folgenden:
f und g
f und h
f und i
g und h
g und i
h und i
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

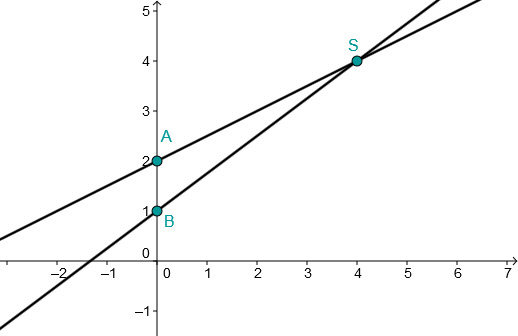
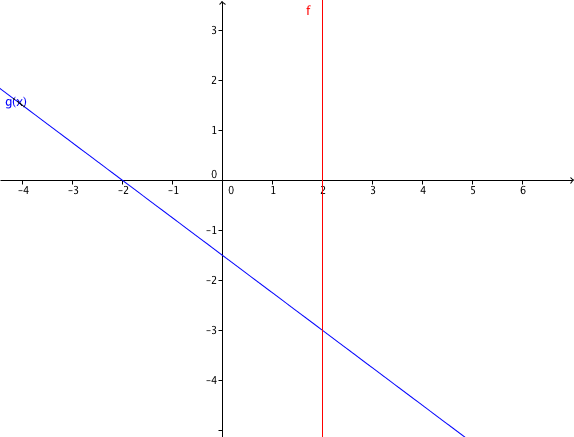
5

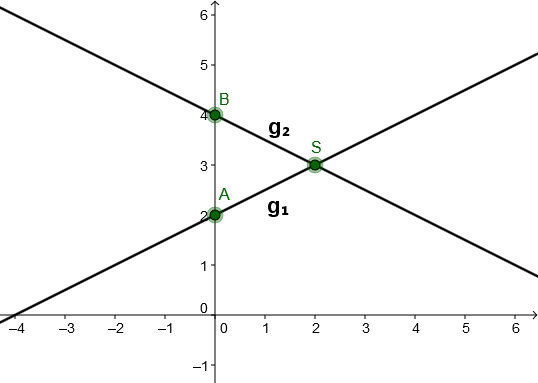
Geradenschnittpunkte berechnen.

Gegeben sind die Funktionsgleichungen zweier Geraden $g_1(x)$ und $g_2\left(x\right)$ . Berechnen Sie den Schnittpunkt beider Geraden und zeichnen Sie die Geraden in ein Koordinatensystem.

Gib den Schnittpunkt in das Eingabefeld ein: "S(1;3)" oder S(1|3)" zum Beispiel.

${\mathrm g}_1\left(\mathrm x\right)=\frac12\mathrm x+2\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=-\frac12\mathrm x+4$

${\mathrm g}_1\left(\mathrm x\right)=2\mathrm x-1\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=-2\mathrm x+1$

${\mathrm g}_1\left(\mathrm x\right)=\frac34\mathrm x-4\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=-\frac12\mathrm x-1$

${\mathrm g}_1\left(\mathrm x\right)=-\frac12\mathrm x+2\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=\frac12\mathrm x+3$

${\mathrm g}_1\left(\mathrm x\right)=\frac23\mathrm x+2\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=\frac12\mathrm x+3$

${\mathrm g}_1\left(\mathrm x\right)=\frac34\mathrm x+1\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=\frac12\mathrm x+2$

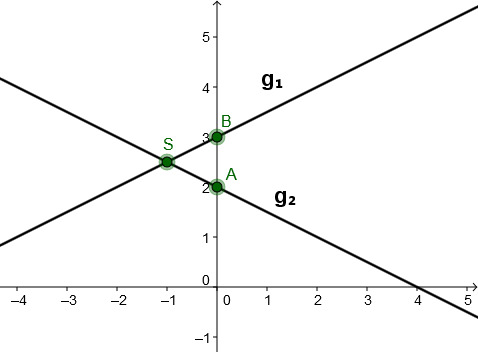
6

Bestimme den Schnittpunkt beider Geraden und zeichne die Graphen in ein Koordinatensystem.

Gib den Schnittpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).

$\mathrm f\left(\mathrm x\right)=0{,}05\mathrm x+20;\;\;\;\;\;\mathrm g\left(\mathrm x\right)=0{,}15\mathrm x+15$

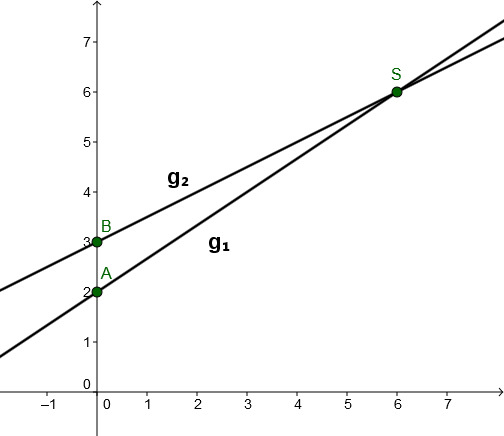
7

Bestimme den Schnittpunkt beider Geraden und zeichne diesen in ein Koordinatensystem.

Gib den Schnittpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).

$\mathrm f\left(\mathrm x\right)=-3\mathrm x+\frac54;\;\mathrm g\left(\mathrm x\right)=-\mathrm x-1$

$\mathrm f:\;2\mathrm y-\mathrm x=3;\;\mathrm g\left(\mathrm x\right)=-\frac12\mathrm x+4$

$\mathrm f\left(\mathrm x\right)=-\frac23\mathrm x-1;\;\mathrm g\left(\mathrm x\right)=\frac16\mathrm x-4$

$\mathrm f:\;\mathrm x=2;\;\mathrm g\left(\mathrm x\right)=-\frac34\mathrm x-\frac32$

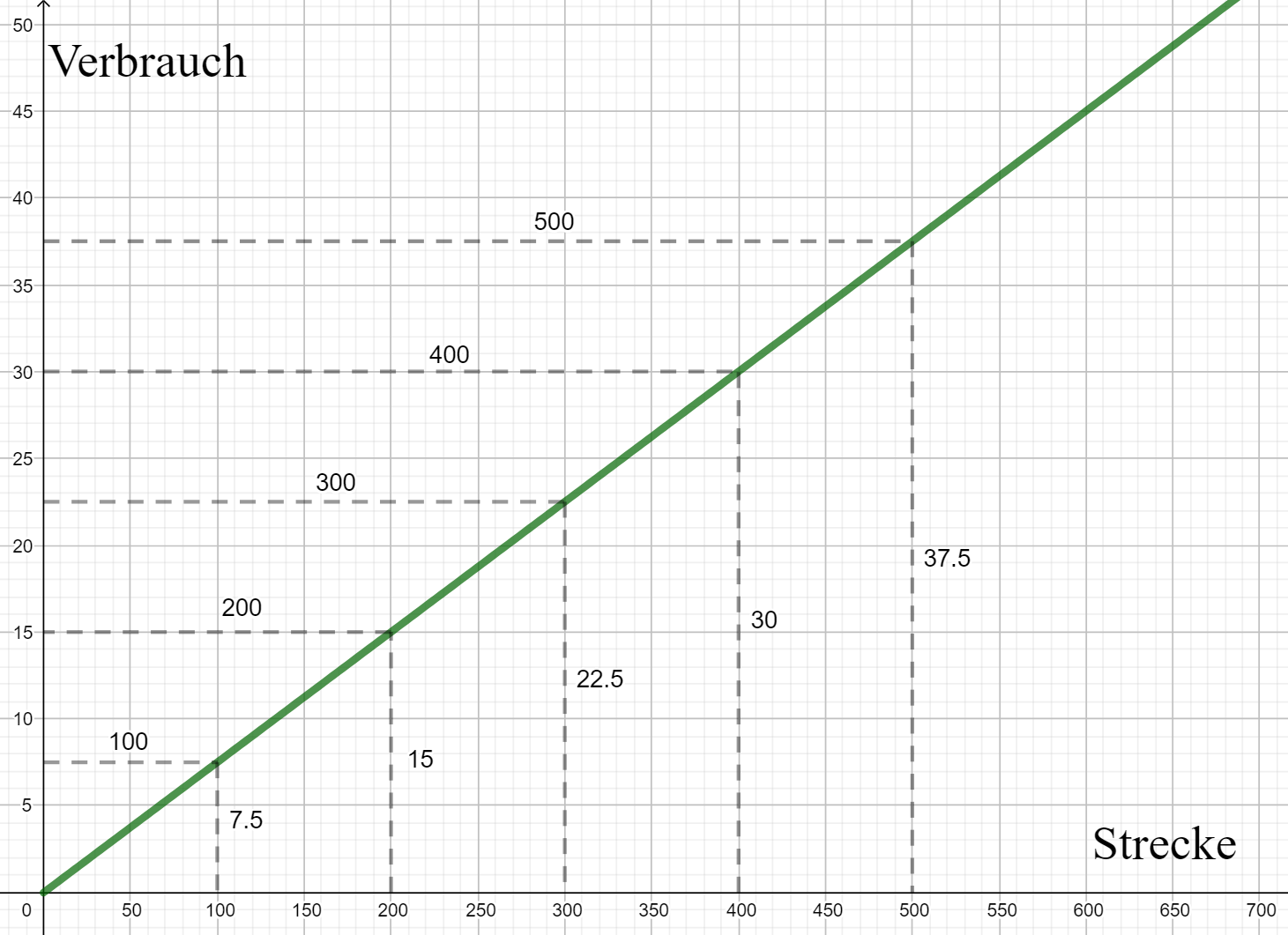
8

Ein Auto besitzt einen Treibstoffvorrat von 56 Liter Benzin. Auf 100km verbraucht es 7,5 Liter.

Erstelle eine Tabelle für den Verbrauch in Litern. Wähle eine Strecke von 0km bis 600km (100km Abstand)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Wachstum
Strecke
0 km
100 km
200 km
300 km
400 km
500 km
600 km
Verbrauch
0 l
7,5 l
15 l
22,5 l
30 l
37,5 l
45 l
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle den Zusammenhang graphisch dar.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Du kannst die Funktion in dein Koordinatensystem einzeichnen, indem du die Punkte aus der Tabelle aus Teilaufgabe $a)$ einträgst und diese anschließend mit einer Geraden verbindest.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Nach wie viel km wäre der Benzinvorrat aufgebraucht? Bei einem Benzinvorrat von 5L soll der Fahrer tanken gehen. Nach wie viel km muss es erfolgen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Zuerst solltest du den Benzinverbrauch als Lineare Funktion darstellen. Diese hat die Form: $f(x)\ =\ mx\ +\ b$ und $x$ steht für die gefahrene Strecke, während $f(x)$ das verbrauchte Benzin angibt. Die Werte von $m$ und $b$ kannst du nun bestimmen, indem du zwei Punkte aus der Wertetabelle einsetzt.
Die lineare Funktion, die den Benzinverbrauch für eine gewisse Anzahl gefahrener Kilometer angibt ist :
Nach wie vielen Kilometern ist der Tank leer?
In den Tank passen $56\,\text{Liter}$ Benzin, diesen Wert kannst du nun als $f(x)$ einsetzen und den zugehörigen $x$ -Wert berechnen:
Der Tank ist also nach ungefähr $746\ \text{km}$ leer.
Nach wie vielen Kilometern muss der Fahrer tanken?
Der Fahrer soll tanken, wenn noch $5 \,\text{Liter}$ Benzin im Tank sind. Da am Anfang $56\,\text{Liter}$ im Tank sind werden also $51\,\text{Liter}$ verbraucht. Das kannst du so in die Funktion einsetzen wie gerade:
Der Fahrer muss also nach $680 \,\text{km}$ zum tanken.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Strecke	0 km	100 km	200 km	300 km	400 km	500 km	600 km
Verbrauch	0 l	7,5 l	15 l	22,5 l	30 l	37,5 l	45 l

9

Gegeben sind die Geraden $g$ : $y=2x-3$ und $h$ : $y=-0{,}5x+4$ .

Berechne den Schnittpunkt der beiden Geraden.

Gib ihn in der Form "(x;y)" in das Eingabefeld ein. Zum Beispiel: $(2{,}5;3)$

Berechne die Fläche, des Dreiecks, das von $g$ und $h$ und der $y$ -Achse gebildet wird.

Die Grundlinie g des Dreiecks ist $7$
Hier nimmt man ausgehend von der Formel zur Berechnung der Fläche eines Dreiecks den Abschnitt zwischen den beiden Schnittpunkten der Geraden mit der $y$ -Achse als Grundlinie. Diese Schnittpunkte werden mit dem Buchstaben $t$ gekennzeichnet. Bei den gegebenen Geraden liegt der Bereich also zwischen $-3$ und $4$ $\Rightarrow$ $g=7$
Die Höhe h ist 2,8
Die Höhe h steht immer senkrecht auf der Grundlinie und ist somit parallel zur x-Achse. Damit entspricht er der Länge vom Ursprung zu dem $x-$ Wert des Schnittpunktes beider Geraden.
$\Rightarrow A=\frac{1}{2}\cdot g\cdot h=\frac{7\cdot2{,}8}{2}=9{,}8$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

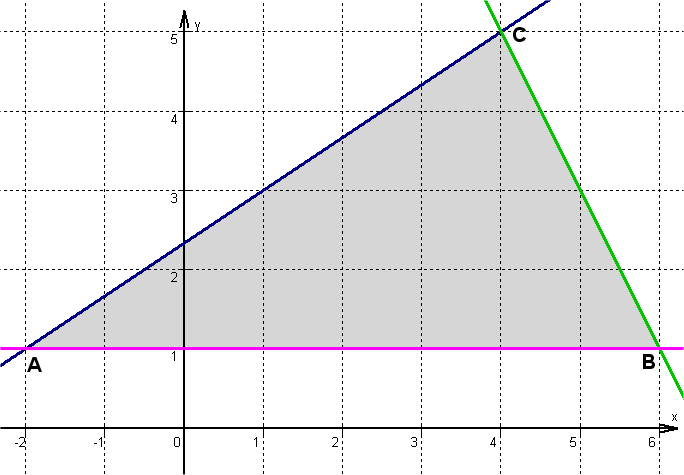
10

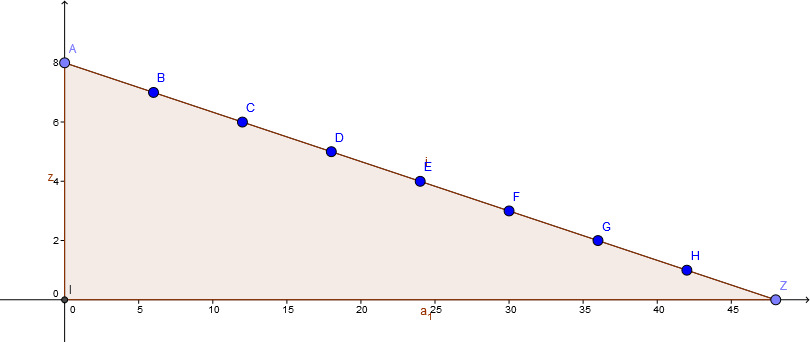
Gegeben sind die drei Punkte $A(-2 | 1)$ , $B(6 | 1)$ und $C(4 | 5)$ .

Stelle die Gleichung der Geraden $AB$ , $AC$ und $BC$ auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Gerade AB:
$A=(-2|1)$ und $B=(6|1)$
Bestimme die Steigung $m$ mit dem Differenzenquotienten.
$m=\frac{1-1}{6-(-2)}=\frac{0}{8}=0$
Die Gerade ist also parallel zur $x$ -Achse.
Der y-Achsenabschnitt $t$ ist also gleich der $y$ -Koordinate der beiden Punkte.
$t=1$
Setze zur Geradengleichung zusammen.
$y=mx+t=0\cdot x+1=1$
Gerade AC:
$A=(-2|1)$ und $C=(4|5)$
Bestimme die Steigung $m$ mit dem Differenzenquotienten.
$m=\frac{5-1}{4-(-2)}=\frac{4}{6}=\frac{2}{3}$
Stelle die Gleichung für den y-Achsenabschnitt auf.
$y=mx+t$
Setze einen Punkt, z.B. $A$ ein.
$1=\frac{2}{3}(-2)+t$
Löse nach $t$ auf.
$t=1-(\frac{-4}{3})=1+\frac{4}{3}=\frac{7}{3}$
Setze zur Geradengleichung zusammen.
$y=mx+t=\frac{2}{3}x+\frac{7}{3}$
Gerade BC:
$B=(6|1)$ und $C=(4|5)$
Bestimme die Steigung $m$ mit dem Differenzenquotienten.
$m=\frac{5-1}{4-6}=\frac{4}{-2}=-2$
Stelle die Gleichung für den y-Achsenabschnitt auf.
$y=mx+t$
Setze einen Punkt, z.B. $B$ ein.
$1=-2\cdot 6+t$
Löse nach t auf.
$t=1-(-2)\cdot 6=1+12=13$
Setze zur Geradengleichung zusammen.
$y=mx+t=-2x+13$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne den Umfang des Dreiecks $ABC$ .
LE

Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand von Punkten berechnen
Der Umfang des Dreiecks berechnet sich aus den Längen der Strecken zwischen den Punkten. Benutzte dazu die bekannte Formel.
$d(P_1,P_2)=\sqrt{(\Delta x)^2+(\Delta y)^2}$
Setze für jede Strecke zwei Punkte ein.
Seite AB:
$\Delta x=-2-6=-8$
$\Delta y=1-1=0$
Setze in die Formel ein. Beachte, dass für Längen nur positive Ergebnisse relevant sind.
$d(A,B)=\sqrt{(-8)^2+0^2}=\sqrt{64}=8$
Diese Seite hat also Länge 8.
Seite AC:
$\Delta x=-2-4=-6$
$\Delta y=1-5=-4$
Setze in die Formel ein. Beachte, dass für Längen nur positive Ergebnisse relevant sind.
$d(A,C)=\sqrt{(-6)^2+(-4)^2}=\sqrt{36+16}$ $=\sqrt{52}\approx7{,}21$
Diese Seite hat also etwa Länge 7,2.
Seite BC:
$\Delta x=6-4=2$
$\Delta y=1-5=-4$
Setze in die Formel ein. Beachte, dass für Längen nur positive Ergebnisse relevant sind.
$d(A,C)=\sqrt{2^2+(-4)^2}=\sqrt{4+16}=\sqrt{20}\approx4{,}47$
Diese Seite hat also etwa Länge 4,5.
$\Rightarrow$ Der Umfang ist gleich 8 + 7,2 + 4,5 = 19,7.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne den Flächeninhalt des Dreiecks $ABC$ .
FE

Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche eines Dreiecks
$A=\frac{1}{2}\cdot \text{Höhe}\cdot \text{Grundseite}$
Wähle AB als Grundseite, da diese parallel zur x-Achse ist. Dadurch ist die Höhe parallel zur y-Achse.
Höhe h ist gleich dem Abstand von $C$ zu $AB$ .
Da die Höhe parallel zur y-Achse ist, berechnet sich der Abstand einfach durch Vergleich der y-Koordinaten.
Der Abstand des Punktes C von der Grundlinie ist $h=5-1=4$
Eingesetzt in die Formel ergibt das: $A=\frac{1}{2}\cdot 4\cdot 8=16$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\displaystyle x\cdot25+y\cdot150$	$=$	$\displaystyle 1200$	$\displaystyle -x\cdot25$
	↓	Stelle die Gleichung so um, dass du eine Geradengleichung erhältst.
$\displaystyle 150\cdot y$	$=$	$\displaystyle -25\cdot x+1200$	$\displaystyle :150$
$\displaystyle y$	$=$	$\displaystyle -\frac{25}{150}\cdot x+\frac{1200}{150}$
	↓	Kürze die Brüche.
$\displaystyle y$	$=$	$\displaystyle -\frac16\cdot x+8$

$\displaystyle \displaystyle\frac14x_P+1$	$=$	$\displaystyle 3x_P+3$	$\displaystyle -3x_p-1$
	↓	Subtrahiere $3x_P$ und 1.
$\displaystyle \displaystyle -\frac{11}{4}x_P$	$=$	$\displaystyle 2$	$\displaystyle \div\left(-\frac{11}4\right)$
	↓	Dividiere durch $-\frac{11}4$ .
$\displaystyle x_p$	$=$	$\displaystyle -\frac{8}{11}$

$\displaystyle \displaystyle-\frac14x_{N_f}+3$	$=$	$\displaystyle 0$	$\displaystyle -3$
$\displaystyle \displaystyle -\frac14x_{N_f}$	$=$	$\displaystyle -3$	$\displaystyle :\frac{1}{4}$
$\displaystyle \displaystyle x_{N_f}$	$=$	$\displaystyle 12$

$\displaystyle 2x-1$	$=$	$\displaystyle -2x+1$	$\displaystyle +2x+1$
$\displaystyle 2x+2x$	$=$	$\displaystyle 1+1$
$\displaystyle 4x$	$=$	$\displaystyle 2$	$\displaystyle :4$
$\displaystyle \mathrm x_S$	$=$	$\displaystyle \frac{1}{2}$
	↓	Setze x in ${\mathrm g}_1(\mathrm x)$ ein.
$\displaystyle y$	$=$	$\displaystyle 2\cdot\frac{1}{2}-1$
$\displaystyle y$	$=$	$\displaystyle 1-1$
$\displaystyle \mathrm y_S$	$=$	$\displaystyle 0$

$\displaystyle g_1(x)$	$=$	$\displaystyle g_2(x)$
$\displaystyle \frac{3}{4}x-4$	$=$	$\displaystyle -\frac{1}{2}x-1$	$\displaystyle +\frac{1}{2}x+4$
$\displaystyle \frac{3}{4}x+\frac{1}{2}x$	$=$	$\displaystyle -1+4$
$\displaystyle 1{,}25x$	$=$	$\displaystyle 3$	$\displaystyle 1{,}25$
$\displaystyle x$	$=$	$\displaystyle \frac{3}{1{,}25}$
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 2{,}4$
	↓	Setze $x_S$ in ${\mathrm g}_1(\mathrm x)$ ein.
$\displaystyle y$	$=$	$\displaystyle \frac{3}{4}\cdot2{,}4-4$
$\displaystyle y$	$=$	$\displaystyle 1{,}8-4$
$\displaystyle \mathrm y_S$	$=$	$\displaystyle -2{,}2$

$\displaystyle \frac12\mathrm x+2$	$=$	$\displaystyle -\frac12\mathrm x+4\\$	$\displaystyle \left\|+\frac12x-2\right.$
$\displaystyle \frac12\mathrm x+\frac12\mathrm x$	$=$	$\displaystyle 4-2$
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 2$
	↓	Setze x in ${\mathrm g}_1\left(\mathrm x\right)$ ein.
$\displaystyle \text{y}$	$=$	$\displaystyle 1+2$
$\displaystyle \mathrm y_S$	$=$	$\displaystyle 3$

$\displaystyle g_1\left(x\right)$	$=$	$\displaystyle g_2\left(x\right)$
$\displaystyle -\frac12\mathrm x+2$	$=$	$\displaystyle \frac12\mathrm x+3\\$	$\displaystyle \left\|+\frac12\mathrm x\right.-3$
$\displaystyle 2-3$	$=$	$\displaystyle \frac{1}{2}x+\frac{1}{2}x$
$\displaystyle \mathrm{x}_S$	$=$	$\displaystyle -1$
	↓	Setze $x_S$ in ${\mathrm g}_1\left(\mathrm x\right)$ ein.
$\displaystyle y$	$=$	$\displaystyle -\frac12\cdot\left(-1\right)+2\\$
$\displaystyle y$	$=$	$\displaystyle \frac{1}{2}+2$
$\displaystyle \mathrm{y}_S$	$=$	$\displaystyle 2{,}5$

$\displaystyle \frac{2}{3}\mathrm{x}+2$	$=$	$\displaystyle \frac{1}{2}\mathrm{x}+3$	$\displaystyle -\frac{1}{2}\mathrm{x}-2$
$\displaystyle \frac{2}{3}\mathrm{x}-\frac{1}{2}\mathrm{x}$	$=$	$\displaystyle 3-2$
	↓	Bringe die Brüche auf den kleinsten gemeinsamen Nenner.
$\displaystyle \frac{4}{6}\mathrm{x}-\frac{3}{6}\mathrm{x}$	$=$	$\displaystyle 3-2$
$\displaystyle \frac{1}{6}x$	$=$	$\displaystyle 1$	$\displaystyle :\frac{1}{6}$
$\displaystyle x$	$=$	$\displaystyle \displaystyle\frac1{\frac16}$
	↓	Du dividierst durch einen Bruch $\rightarrow$ Multipliziere mit dem Kehrwert.
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 6$

$\displaystyle \frac34\mathrm x+1$	$=$	$\displaystyle \frac12\mathrm x+2$	$\displaystyle -\frac12x-1$
$\displaystyle \frac34\mathrm x-\frac12\mathrm x$	$=$	$\displaystyle 2-1$
	↓	Bringe die Brüche auf den kleinsten gemeinsamen Nenner .
$\displaystyle \frac34\mathrm x-\frac24\mathrm x$	$=$	$\displaystyle 2-1$
$\displaystyle \frac14\mathrm x$	$=$	$\displaystyle 1$	$\displaystyle :\frac14$
$\displaystyle x$	$=$	$\displaystyle \displaystyle\frac1{\frac14}$
	↓	Du dividierst durch einen Bruch $\rightarrow$ Multipliziere mit dem Kehrwert.
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 4$

$\displaystyle 0{,}05\mathrm{x}+20$	$=$	$\displaystyle 0{,}15\mathrm{x}+15$	$\displaystyle -0{,}05\mathrm x-15$
$\displaystyle 20-15$	$=$	$\displaystyle 0{,}15\mathrm x-0{,}05\mathrm x$
	↓	Subtrahiere und vertausche die Seiten.
$\displaystyle 0{,}10\mathrm x$	$=$	$\displaystyle 5$	$\displaystyle :0{,}1$
$\displaystyle \mathrm x$	$=$	$\displaystyle \frac5{0{,}1}$
	↓	Dividiere.
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 50$

$\displaystyle \mathrm y$	$=$	$\displaystyle 0{,}05\cdot50+20$
	↓	Multipliziere.
$\displaystyle \mathrm y$	$=$	$\displaystyle 2{,}5+20$
	↓	Addiere.
$\displaystyle \mathrm y_S$	$=$	$\displaystyle 22{,}5$

$\displaystyle -3\mathrm{x}+\frac{5}{4}$	$=$	$\displaystyle - x -1$	$\displaystyle +3\mathrm x+1$
$\displaystyle -\mathrm x+3\mathrm x$	$=$	$\displaystyle \frac54+1$
	↓	Addiere
$\displaystyle 2x$	$=$	$\displaystyle \frac94$	$\displaystyle \colon 2$
$\displaystyle x$	$=$	$\displaystyle \frac{9}{8}=1{,}125$

$\displaystyle y$	$=$	$\displaystyle -\frac98 -1$
	↓	Subtrahiere
$\displaystyle y$	$=$	$\displaystyle -2{,}125$

$\displaystyle 2y - x$	$=$	$\displaystyle 3$	$\displaystyle +x$
$\displaystyle 2y$	$=$	$\displaystyle 3 + x$	$\displaystyle \colon 2$
$\displaystyle y$	$=$	$\displaystyle \frac32+\frac{\mathrm x}2$

$\displaystyle \frac32+\frac{\mathrm x}2$	$=$	$\displaystyle -\frac12x+4$	$\displaystyle +\frac{\mathrm x}2-1{,}5$
$\displaystyle \frac{\mathrm x}2+\frac{\mathrm x}2$	$=$	$\displaystyle 4-1{,}5$
	↓	Addiere und subtrahiere
$\displaystyle x$	$=$	$\displaystyle 2{,}5$

$\displaystyle y$	$=$	$\displaystyle \frac32+\frac{2{,}5}2$
	↓	Addiere
$\displaystyle y$	$=$	$\displaystyle 2{,}75$

$\displaystyle -\frac23\mathrm x-1$	$=$	$\displaystyle \frac16\mathrm x-4$	$\displaystyle +\frac23\mathrm x+4$
$\displaystyle \frac16\mathrm x+\frac23\mathrm x$	$=$	$\displaystyle -1 + 4$
	↓	Addiere.
$\displaystyle \frac56 \mathrm x$	$=$	$\displaystyle 3$	$\displaystyle :\frac56$
$\displaystyle x$	$=$	$\displaystyle 3\;:\;\frac56$
	↓	Dividiere durch einen Bruch $\rightarrow$ Multipliziere mit dem Kehrwert
$\displaystyle x$	$=$	$\displaystyle 3\cdot\frac65$
	↓	Multipliziere.
$\displaystyle x$	$=$	$\displaystyle \frac{18}{5}$

$\displaystyle y$	$=$	$\displaystyle \frac16\cdot\frac{18}5-4$
	↓	Multipliziere.
$\displaystyle y$	$=$	$\displaystyle \frac35-4$
	↓	Subtrahiere
$\displaystyle y$	$=$	$\displaystyle - 3{,}4$

$\displaystyle y$	$=$	$\displaystyle -\frac34\cdot2-\frac32$
	↓	Multipliziere.
$\displaystyle y$	$=$	$\displaystyle -\frac32-\frac32$
	↓	Subtrahiere.
$\displaystyle y$	$=$	$\displaystyle -\frac62$
	↓	Dividiere.
$\displaystyle y$	$=$	$\displaystyle -3$

$\displaystyle 2x-3$	$=$	$\displaystyle -0{,}5x+4$	$\displaystyle +0{,}5x\ \|+3$
$\displaystyle 2{,}5x$	$=$	$\displaystyle 7$	$\displaystyle :2{,}5$
$\displaystyle x$	$=$	$\displaystyle 2{,}8$
$\displaystyle y$	$=$	$\displaystyle 2\cdot2{,}8-3$
	↓	Beachte "Punkt vor Strich"
$\displaystyle y$	$=$	$\displaystyle 5{,}6-3=2{,}6$

Gemischte Aufgaben zu linearen Funktionen - Geraden

Zeichne die Graphen

Bestimmung der Nullstellen

Bestimmung des Schnittpunkts

Monatsrechnung bei 40 Minuten

Monatsrechnung bei 80 Minuten

Monatsrechnung bei 120 Minuten

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Teilaufgabe 1

Darstellung im Diagramm

Teilaufgabe 2

f(x):y=mfx+bf\text f(x):y=m_fx+b_ff(x):y=mf​x+bf​

g(x):y=mgx+bg\text g(x):y=m_gx+b_gg(x):y=mg​x+bg​

h(x):y=mhx+bh\text h(x):y=m_hx+b_hh(x):y=mh​x+bh​

i(x):y=mix+bi\text i(x):y=m_ix+b_ii(x):y=mi​x+bi​

Hast du eine Frage oder Feedback?

Schnittpunkt P(xp∣yp)P(x_p|y_p)P(xp​∣yp​) von g und h

Hast du eine Frage oder Feedback?

Schnittpunkt T(xT∣yT)T(x_T|y_T)T(xT​∣yT​) von h und i

Schnittpunkt Q(xQ∣yQ)Q(x_Q|y_Q)Q(xQ​∣yQ​) von g und i

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Geradenschnittpunkte berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Bestimmung des Schnittpunkts

Zeichnung

Zeichnung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nach wie vielen Kilometern ist der Tank leer?

Nach wie vielen Kilometern muss der Fahrer tanken?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gerade AB:

Gerade AC:

Gerade BC:

m=5−14−6=4−2=−2m=\frac{5-1}{4-6}=\frac{4}{-2}=-2m=4−65−1​=−24​=−2

Hast du eine Frage oder Feedback?

Seite AB:

Δx=−2−6=−8\Delta x=-2-6=-8Δx=−2−6=−8

Δy=1−1=0\Delta y=1-1=0Δy=1−1=0

Seite AC:

Δx=−2−4=−6\Delta x=-2-4=-6Δx=−2−4=−6

Δy=1−5=−4\Delta y=1-5=-4Δy=1−5=−4

Seite BC:

Δx=6−4=2\Delta x=6-4=2 Δx=6−4=2

Δy=1−5=−4\Delta y=1-5=-4Δy=1−5=−4

d(A,C)=22+(−4)2=4+16=20≈4,47d(A,C)=\sqrt{2^2+(-4)^2}=\sqrt{4+16}=\sqrt{20}\approx4{,}47d(A,C)=22+(−4)2​=4+16​=20​≈4,47

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$\text f(x):y=m_fx+b_f$

$\text g(x):y=m_gx+b_g$

$\text h(x):y=m_hx+b_h$

$\text i(x):y=m_ix+b_i$

Schnittpunkt $P(x_p|y_p)$ von g und h

Schnittpunkt $T(x_T|y_T)$ von h und i

Schnittpunkt $Q(x_Q|y_Q)$ von g und i

$m=\frac{5-1}{4-6}=\frac{4}{-2}=-2$

$\Delta x=-2-6=-8$

$\Delta y=1-1=0$

$\Delta x=-2-4=-6$

$\Delta y=1-5=-4$

$\Delta x=6-4=2$

$\Delta y=1-5=-4$

$d(A,C)=\sqrt{2^2+(-4)^2}=\sqrt{4+16}=\sqrt{20}\approx4{,}47$