2017
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
- 2
Gib die Koordinaten des Pfeils an, wenn gilt: A (40 | 35) , B (-62 | 80).
- 3
An folgenden Wintertagen wurde an einem Ort jeweils um 12:00 Uhr mittags die Außentemperaturgemessen.
Wie viel Grad Celsius hatte es am 25.12. um 12:00 Uhr an diesem Ort, wenn der Durchschnittder Messwerte an den vier Tagen 6,0 °C beträgt?

- 4
Bei welchen der folgenden Terme erhält man das Ergebnis -64?
Kreuze die richtigen Terme an.
- 5
Ergänze die Lücken so, dass äquivalente Terme entstehen .
- 6
Wie viele natürliche Zahlen gibt es zwischen und Wähle aus.
- 7
Setze das richtige Zeichen ( < , > oder =) ein.
- 8
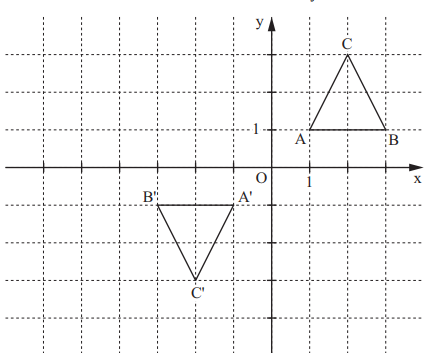
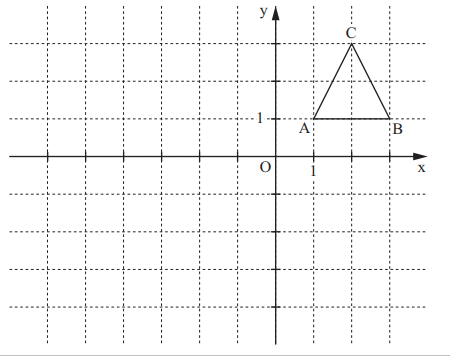
Das Dreieck ABC wird durch Punktspiegelung am Punkt O(0|0) auf das Dreieck A'B'C'abgebildet.
Zeichne das Dreieck A'B'C' in das Koordinatensystem ein.
- 9
In einem Beutel mit Losen befinden sich 20 Nieten, 2 Limonaden-Gutscheine, 1 Fußball und 2 Apfelschorlen-Gutscheine.
Gib die Wahrscheinlichkeit an, dass man beim erstmaligen Ziehen eines Loses einen Getränkegutschein zieht.
- 10
Stelle eine passende Gleichung zu folgender Aussage auf, ohne diese zu lösen:
„Ich denke mir eine Zahl und potenziere sie mit 5. Anschließend addiere ich 200 und erhalte -43.“
- 11
Lisbeth legt bei ihrer Radtour an elf Tagen jeweils 50 Kilometer zurück.
Wie viele Kilometer müsste sie täglich fahren, wenn sie die gleiche Tour in zehn Tagen meistern will?
- 12
Gib an, wie groß der Umfang U eines kreisförmigen Blumenbeets ist, wenn der Radius beträgt.
- 13
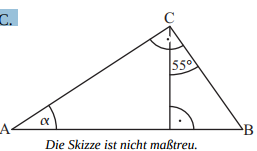
Bestimme das Maß des Winkels im Dreieck ABC.
- 14
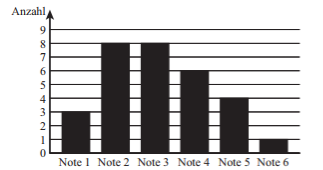
Im Säulendiagramm ist das Ergebnis der letzten Mathematikschulaufgabe der Klasse 8a dargestellt. Die Klasse besteht aus 30 Schülern. Wie viel Prozent der Schüler erhielten die Note 4?
Ergebnis ohne Prozentzeichen!
- 15
Wahr oder falsch. Kreuze an.
Nebenwinkel sind immer maßgleich.
Stufenwinkel sind immer maßgleich.
Wechselwinkel sind immer maßgleich.
- 16
Jonathan hat 150 ml Wasser aus einer Flasche mit einem Inhalt von 500 ml getrunken.
Wie viel Prozent Wasser befindet sich noch in der Flasche?
- 17
Gib die Lösungsmenge der folgenden Gleichung mit an:
- 18
Für welche der folgenden Grundmengen ist die Lösungsmenge der Ungleichung die leere Menge? Wähle jeweils aus.
Grundmenge:
Grundmenge
Grundmenge
- 19
Anton rechnet folgende Aufgabe an der Tafel:
Helena meldet sich und sagt, dass Antons Ergebnis lauten muss. Begründe ohne Rechnung, dass Helena recht hat.
(Anmerkung von serlo.org: In der Angabe sollte ergänzt werden, dass man weiß, dass eine der Antworten richtig ist.)
- 20
Subtrahiert man vom Produkt aus 12 und 7 das Dreifache einer gedachten Zahl, so erhält man 48.
Welche der folgenden Gleichungen passt zum Text? Wähle aus.
- 21
In einem Werbeprospekt findet Tanja folgende Anzeige: „Vor einer Woche gab es auf alle Waren 20% Rabatt, in dieser Woche gibt es auf die reduzierten Preise nochmals 10% Rabatt!“
Tanja freut sich: „Klasse! Dann spare ich bei meinem 100-€-Kleid nicht nur 20%, sondern sogar 30%!“Hat Tanja recht? Begründe.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?