Das Integral ist ein Oberbegriff für das bestimmtes und unbestimmtes Integral. Ein bestimmtes Integral liefert einen Zahlenwert, während ein unbestimmtes Integral eine Funktion liefert. Die Integralrechnung steht in engem Zusammenhang mit der Differentialrechnung.

Die Integralrechnung ist motiviert durch die Berechnung von Flächeninhalten, die eine krummlinige Grenze haben.
Das bestimmte Integral berechnet nämlich die Fläche zwischen dem Graph einer Funktion und der -Achse.
Notation und Bezeichnungen
"das Integral über im Intervall "
Das mathematische Zeichen für das Integral ist .
gibt die Variable an, über die integriert wird.
Man kann sich und als eine Klammer vorstellen. Ein Integral beginnt immer mit und wird mit abgeschlossen.
Die Variable ist hier austauschbar. Steht am Ende des Integrals , so wird über die Variable integriert.
Beispiel: Bei wird über integriert.
und heißen Integrationsgrenzen.
Anschauliche Erklärung
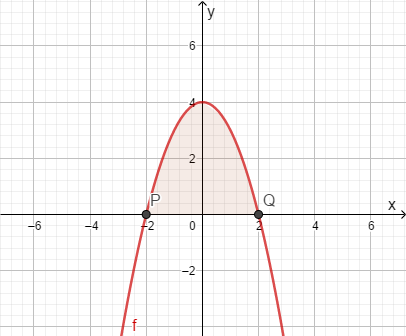
Die schwarz eingezeichnete Funktion ist mit Definitionsbereich .
Es soll die Fläche im Intervall bis bestimmt werden, die der Funktionsgraph mit der -Achse einschließt, diese Fläche wird mit bezeichnet und ist in der Grafik rot eingefärbt.
Mithilfe der Formel für die Flächenberechnung eines Dreiecks erhält man .
Es wäre also wünschenswert, dass der Integralbegriff erfüllt. Man wird später sehen, dass dies gilt.

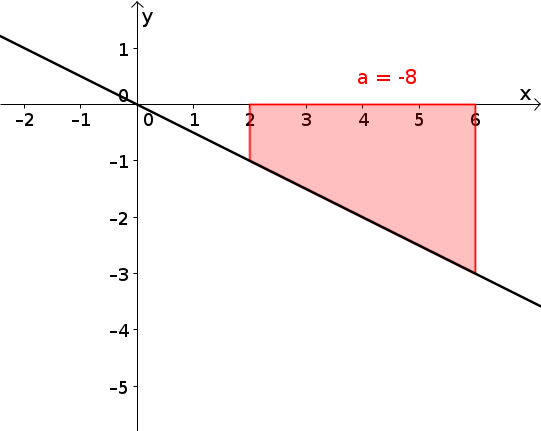
Die schwarz eingezeichnete Funktion ist mit Definitionsbereich .
Es soll die Fläche im Intervall von 2 bis 6 bestimmt werden, die der Funktionsgraph mit der -Achse einschließt. Diese Fläche wird mit bezeichnet und ist in der Grafik rot eingefärbt.
Mithilfe der Formel für die Flächenberechnung eines Trapezes erhält man .
Da die Fläche aber unterhalb der -Achse verläuft, soll das Integral einen negativen Wert liefern.
Es wäre also wünschenswert, dass der Integralbegriff erfüllt. Man wird später sehen, dass dies gilt.
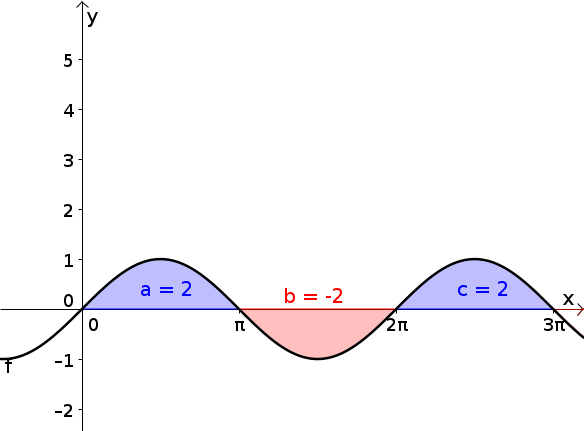
Falls nicht nur positive Werte hat, soll das Integral die Flächenbilanz zwischen dem Graphen von und der -Achse sein. Flächen oberhalb der -Achse werden dabei positiv gewertet, Flächen unterhalb der -Achse negativ.
Die schwarz eingezeichnete Funktion ist . Es soll über die Funktion von bis integriert werden.
Das Integral von ist dann die Summe der gefärbten Flächeninhalte, wobei die Blauen ein positives und die Roten ein negatives Vorzeichen haben. Das Integral von bis wäre also z.B.
Herleitung
Gegeben sei eine stetige Abbildung , die auf dem Intervall definiert ist. Man möchte die Fläche zwischen und der -Koordinate auf dem Intervall bestimmen. Man erhält eine grobe Näherung der Fläche, wenn man das betrachtete Intervall in mehrere Teilintervalle zerlegt. In jedem dieser Teilintervalle lässt sich die Funktion durch ein Rechteck annähern.
Bei der Obersumme bzw. Untersumme wählt man den größten bzw. den kleinsten Funktionswert des betrachteten Teilintervalls als höchsten Punkt des Rechtecks.
Das Integral lässt sich als Grenzwert von Ober- bzw. Untersummen auffassen.
Hauptsatz der Differential- und Integralrechnung
Der Hauptsatz der Differential- und Integralrechnung (HDI) oder auch Fundamentalsatz der Analysis stellt einen Zusammenhang zwischen Ableitung und Integration dar.
Ist eine stetige Funktion und ihre Stammfunktion, dann gilt:
Integral berechnen
Um den Wert eines Integrals zu berechnen, bildet man eine Stammfunktion und wertet diese an den Stellen und , des betrachteten Intervalls aus. Der gesuchte Wert ist dann .
Beispiele
Diese Rechnungen sind also mit den Beispielen aus dem Abschnitt "Anschauliche Erklärung" konsistent (wobei beim dritten Beispiel die Additivitätseigenschaft benutzt wurde, siehe unten).
Rechenregeln
Von Flächen und Funktionen weißt du vielleicht schon, dass du sie addieren und subtrahieren kannst. Hier sind ein paar wichtige Rechenregeln von Integralen aufgelistet.
Obere Grenze = Untere Grenze
Du integrierst über einem Punkt, also ist die Fläche nur eine Linie. Linien haben Breite und eine Länge . Der Flächeninhalt ergibt sich aus , also ist auch das Integral gleich .
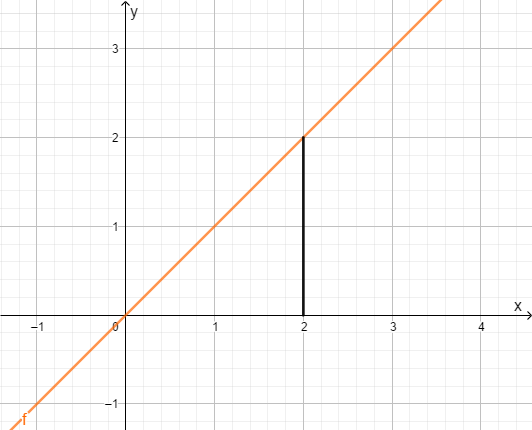
Beispiel:
Umkehren der Grenzen
Beispiel:
und
Additivitätseigenschaft
Herleitung:
Also:
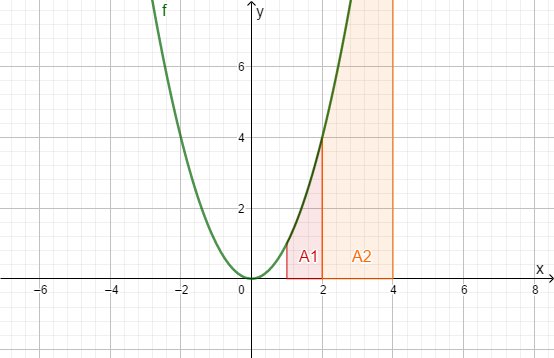
Beispiel:
Erste Linearitätseigenschaft
Beispiel:
Zweite Linearitätseigenschaft
Beispiel:
Monotonieeigenschaft
Beispiel:
Für alle gilt:
Also:
Punktsymmetrische Funktionen
Für eine zum Ursprung punktsymmetrische Funktion , also , gilt:
Beispiel:
ist eine zum Ursprung punktsymmetrische Funktion. Da
Achsensymmetrische Funktionen
Für eine zur -Achse achsensymmetrische Funktion gilt:
Beispiel:
ist eine zur -Achse achsensymmetrische Funktion.
Betrag eines Integrals
Beispiel:
Gegeben ist .
Wegen der Punktsymmetrie von gilt:
und aufgrund der Additivität folgt:
mit Auflösen des Betrags folgt:
.
Bilde die Stammfunktion:
Also ist erfüllt.
Wichtige Begriffe
Bestimmtes und unbestimmtes Integral
Das unbestimmte Integral besitzt im Vergleich zum bestimmten Integral keine Grenzen.
Bei einem bestimmten Integral berechnet man den Flächeninhalt zwischen dem Graphen einer Funktion und der -Achse. Als Lösung bekommt man eine Zahl.
Bei einem unbestimmten Integral erhält man als Lösung eine Funktion, eine sogenannte Stammfunktion.
Integralfunktion
Integralfunktionen sind Funktionen der Form .
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Integralen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
