Ein lineares Gleichungssystem setzt sich aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen) zusammen. Linear heißt hierbei, dass jede Variable höchstens mit dem Exponenten auftaucht.
Um ein lineares Gleichungssystem eindeutig lösen zu können, braucht man mindestens ebenso viele Gleichungen wie Unbekannte.
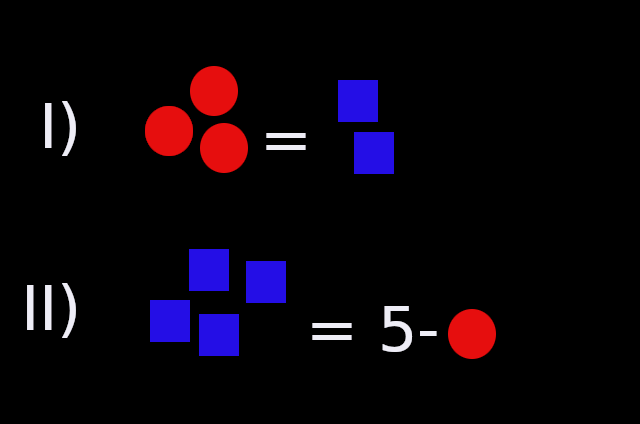
Beispiel zur Veranschaulichung:
Gibt es also zwei unbekannte Größen (z.B. und oder und ), benötigt man auch mindestens zwei Gleichungen zum Lösen.
Die Gleichungen werden mit römischen Zahlen nummeriert und die Variablen passend untereinander angeordnet; wie hier im Beispiel also die Terme mit untereinander, dann die Terme mit .
Detaillierte Einführung
Eine schrittweise Einführung zum Thema findest du im Kurs Einführung in lineare Gleichungssysteme - Teil 1.
Bestimmtheit von Gleichungssystemen
Mehr gesuchte Variablen als Gleichungen
Besitzt ein Gleichungssystem mehr unbekannte Variablen als Gleichungen, kann dieses meist nicht eindeutig gelöst werden. Im Beispiel gibt es drei Unbekannte, aber nur zwei Gleichungen. In diesem Fall spricht man von einem unterbestimmten Gleichungssystem.
Es kann zudem auch vorkommen, dass ein solches Gleichungssystem keine Lösung aufweist. Dieser Fall wird in Lösbarkeit von linearen Gleichungssystemen genauer erläutert.
Beispiel:
Gleich viele gesuchte Variablen wie Gleichungen
Bei einem Gleichungssystem, welches genau gleich viele unbekannte Variablen wie Gleichungen besitzt, kann im Allgemeinen exakt eine Lösung bestimmt werden, das Gleichungssystem ist also eindeutig lösbar. Dies ist der Normalfall.
Es gibt dabei zwei Ausnahmen:
Wenn zwei oder mehr Gleichungen voneinander linear abhängig sind, dann ist das Gleichungssystem wiederum auch nicht eindeutig lösbar, besitzt also eine unendlich Anzahl von Lösungskombinationen.
Es kann auch vorkommen, dass das Gleichungssystem keine Lösung aufweist. Dies wird unter Lösbarkeit von linearen Gleichungssystemen genauer beschrieben.
Beispiel:
Mehr Gleichungen als gesuchte Variablen
Weist ein Gleichungssystem mehr Gleichungen als gesuchte Variablen auf, gibt es im Allgemeinen keine Lösung. In einem solchen Fall spricht man von einem überbestimmten Gleichungssystem.
Wiederum als Ausnahme gilt, wenn mehrere Gleichungen voneinander linear abhängig sind. Dies kann dazu führen, dass das Gleichungssystem entweder eindeutig lösbar wird oder wir sogar ein unterbestimmtes Gleichungssystem haben.
Beispiel:
Gleichungssysteme lösen
Ein Gleichungssystem zu lösen bedeutet alle Variablen so zu bestimmen, dass alle Gleichungen des Systems erfüllt werden. Es gibt fünf verschiedene Verfahren, ein Gleichungssystem zu lösen:
Das Additionsverfahren (wenn sich durch die Addition der Gleichungen eine der unbekannten Größen aufhebt)
Das Einsetzungsverfahren (wenn sich sehr leicht nach einer Variablen auflösen lässt)
Das Gleichsetzungsverfahren (wenn man zwei Gleichungen leicht nach der gleichen Variablen auflösen kann)
Das Gaußverfahren (wenn es sich um sehr viele unterschiedliche Variablen handelt)
Cramersche Regel (wenn es sich um ein kleines Gleichungssystem handelt und nur bei eindeutig lösbaren Gleichungssystemen sinnvoll)
Gleichungssystem als Matrix darstellen
Ein lineares Gleichungssystem lässt sich immer als erweiterte Koeffizienten-Matrix schreiben.
Beispiel:
Gleichungssystem
Erläuterung
In die Matrix werden die Koeffizienten übertragen. Die konstanten Terme werden dabei ganz rechts eingetragen und durch einen Strich abgetrennt.
Matrix
Die Schreibweise eines Gleichungssystems als erweiterte Koeffizientenmatrix ist hilfreich, um Aussagen über die Lösbarkeit des Gleichungssystems zu treffen und um die Lösung(en) zu berechnen.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Anwendungsaufgaben zu Gleichungssystemen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Additionsverfahren
- Einsetzungsverfahren
- Cramersche Regel
- Gaußverfahren
- Lösbarkeit von linearen Gleichungssystemen
