Aufgaben zu quadratischen Gleichungen
- 1
Beim Lösen quadratischer Gleichungen erhält man z. B. Ausdrücke der folgenden Art. Vereinfache diese:
- 2
Löse die folgenden quadratischen Gleichungen mit quadratischer Ergänzung.
Die Lösungen kannst du durch ein Semikolon getrennt in das Lösungsfeld eingeben.
Sie die Lösungen z.B. und , so kannst du entweder "" oder "" (ohne die Anführungszeichen) eingeben.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Ergänzung
↓ Quadratisch ergänzen mit .
↓ Zur 1. binomischen Formel zusammenfassen.
↓ Zusammenfassen
↓ Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Ergänzung
↓ Ergänze quadratisch mit .
↓ Fasse zusammen.
↓ Fasse als 1. binomische Formel zusammen.
↓ Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Ergänzung
↓ 0,5 ausklammern.
↓ ↓ Zur 2. binomischen Formel zusammenfassen.
↓ ↓ Gleichung umformen.
↓ Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Ergänzung
↓ ↓ Ergänze quadratisch mit .
↓ Fasse als 2. binomische Formel zusammen.
↓ ↓ Fasse zusammen.
↓ Ziehe Wurzel auf beiden Seiten.
↓ Forme weiter um.
↓ Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Ergänzung
↓ ↓ Ergänze quadratisch mit .
↓ Fasse zu 1. binomischen Formel zusammen.
↓ ↓ Erweitere die Brüche auf den gemeinsamen Nenner.
↓ Fasse zusammen.
↓ Forme weiter um.
↓ Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Ergänzung
↓ Alle Summanden auf eine Seite bringen.
↓ Den Faktor 2 ausklammern.
↓ ↓ Zur 2. binomischen Formel zusammenfassen.
↓ ↓ Die Gleichung nach x auflösen.
↓ Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
- 3
Löse die folgenden Gleichungen und überprüfe dein Ergebnis mit dem Satz von Vieta.
Gib die Lösung in der Form "" an. Zum Beispiel: ""
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
Die Lösung der Gleichung kannst du mit der Mitternachtsformel oder pq-Formel berechnen:
Lösung mit der Mitternachtsformel
, und
Die drei Koeffizienten der Gleichung in die Mitternachtsformel einsetzen.
Lösung mit der pq-Formel
und
Die 2 Koeffizienten in die pq-Formel einsetzen:
Überprüfung der Lösung mit dem Satz von Vieta
Für eine Gleichung der Form erfüllen die Lösungen und nach dem Satz von Vieta folgende Bedingungen:
Setze und in die Formeln ein und prüfe, ob die Gleichungen und stimmen:
Die berechneten Ergebnisse sind richtig.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
Die Lösung der Gleichung kannst du mit der Mitternachtsformel oder pq-Formel berechnen:
Lösung mit der Mitternachtsformel
und
Die Lösungen sind also und .
Lösung mit der pq-Formel
und
Die 2 Koeffizienten in die pq-Formel einsetzen:
Überprüfung der Lösung mit dem Satz von Vieta
Für eine Gleichung der Form erfüllen die Lösungen und nach dem Satz von Vieta folgende Bedingungen:
Setze und in die Formeln ein und prüfe, ob die Gleichungen und stimmen:
Die berechneten Ergebnisse sind richtig.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
Die Lösung der Gleichung kannst du mit der Mitternachtsformel oder pq-Formel berechnen:
Lösung mit Mitternachtsformel
Die Koeffizienten sind .
Eingesetzt in die Mitternachtsformel erhältst du:
↓ Multipliziere mit dem Kehrbruch.
und
Lösung mit der pq-Formel
Die pq-Formel lässt sich nur auf Gleichungen der Form anwenden. Klammere also zuerst aus:
und
Die 2 Koeffizienten in die pq-Formel einsetzen:
Überprüfung der Lösung mit dem Satz von Vieta
Für eine Gleichung der Form erfüllen die Lösungen und nach dem Satz von Vieta folgende Bedingungen:
Geg:
Da ist muss man zuerst ausklammern, um den Satz von Vieta anwenden zu können.
Hierauf kannst du den Satz von Vieta nun anwenden.
Setze und in die Formeln ein und prüfe, ob die Gleichungen und stimmen:
Die berechneten Ergebnisse sind richtig.
Hast du eine Frage oder Feedback?
- 4
Bestimme die Lösungsmenge der folgenden Gleichungen () und kontrolliere dein Ergebnis graphisch, z. B. mit Hilfe eines Funktionsplotters.
Gib die Lösung in der Form "" in das Eingabefeld ein. Zum Beispiel: "". Bei einer Lösung reicht zum Beispiel "".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichungen
Nun kann man die Diskriminante D berechnen:
Da , erhalten wir zwei Lösungen. Man kann nun die Mitternachtsformel anwenden. Die Lösungen lauten:
Die Lösungsmenge lautet . Der gezeichnete Graph sieht so aus:
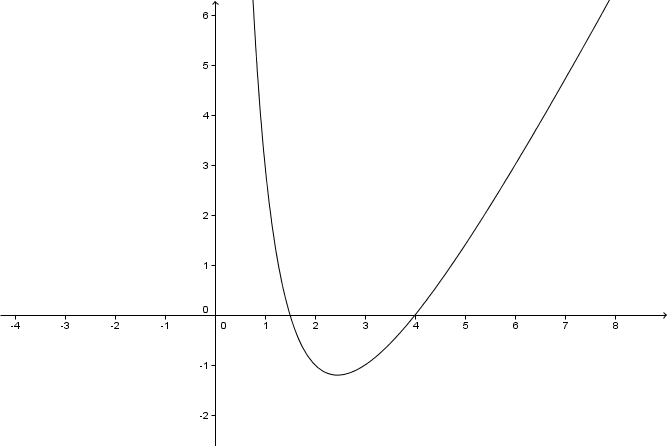
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Nun kann man die Diskriminante D berechnen:
Da , erhalten wir eine Lösungen. Man kann nun die Mitternachtsformel anwenden. Die Lösung lautet:
Die Lösungsmenge lautet .
Hast du eine Frage oder Feedback?
- 5
Löse die angegebenen Gleichungen.
Gib die Lösungen in der Form "" an. Zum Beispiel: ""
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungen
Damit der Term auf der linken Seite gleich ist, muss einer der beiden Faktoren gleich sein. Also entweder:
Dann erhältst du die Lösung . Oder:
Dann erhältst du die Lösung
Insgesamt hast du also die Lösungsmenge .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungen
Damit der Term auf der linken Seite gleich ist, muss der Faktor gleich sein. Mit:
kommst du auf das Ergebnis .
Diese Lösung ist eine zweifache Lösung!
Die Lösungsmenge ist .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lösen quadratischer Gleichungen
Diese Gleichung kannst du mit der Mitternachtsformel lösen:
Unter der Wurzel ergibt sich der Wert , damit gibt es nur genau eine Lösung und zwar: .
Die Lösungsmenge ist .
Hast du eine Frage oder Feedback?
- 6
Berechne möglichst geschickt die Lösungen der folgenden Gleichungen. Überprüfe deine Ergebnisse grafisch, z. B. mithilfe eines Funktionsplotters.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung
↓ Diskriminante berechnen
↓ daher 2 Lösungen
↓ In die Mitternachtsformel einsetzen dabei die berechnete Diskriminante einsetzen
↓ berechnen
Graphen zeichnen

Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung
Gleichung bestimmen
↓ Klammer mit Hilfe der 1. Binomischen Formel ausmultiplizieren.
↓ Gleiche Elemente zusammenfassen
↓ Diskriminante berechnen
↓ daher 2 Lösungen
↓ In die Mitternachtsformel einsetzten, dabei die berechnete Diskriminante einsetzen.
Graphen zeichnen

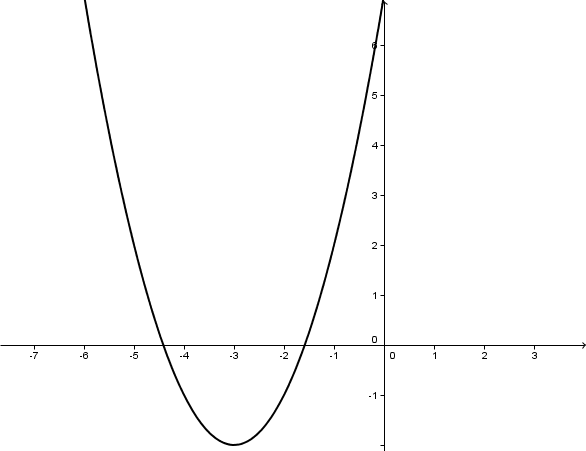
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel (Quadratische Lösungsformel)
Quadratische Gleichung lösen
↓ Stelle die Gleichung so um, dass auf einer Seite 0 ist
↓ Setze in die Mitternachtsformel ein
↓ ausrechnen
Graphische Darstellung
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Äquivalenzumformungen
Lösungen von Gleichungen
Graphen zeichen

Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel (Quadratische Lösungsformel)
Lösung mit Hilfe der pq-Formel:
↓ Die Gleichung liegt in der Normalform vor.
Nach der pq-Formel gilt:
mit und
↓ Einsetzen der Werte
↓ Vereinfachen der Wurzel
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Quadratische Gleichung
↓ Gleiches zusammenfassen
↓ Hast du eine Frage oder Feedback?
- 7
Gib jeweils eine quadratische Gleichung mit der angegebenen Eigenschaft an.
Die Gleichung hat nur die Lösung –2.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Die Gleichung hat nur die Lösung –2.
Zerlegung in Linearfaktoren.
Zusammenfassen.
Hast du eine Frage oder Feedback?
Die Gleichung hat keine Lösungen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Damit die Gleichung keine Lösung hat muss eine unwahre Aussage entstehen.
Dies geschieht beispielsweise bei allen Gleichungen, auf deren einer Seite und auf deren anderen eine negative Zahl steht.
Beispielsweise:
Hast du eine Frage oder Feedback?
Die Gleichung hat die Lösungen –2 und 2.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Die Gleichung hat die Lösungen –2 und 2.
Zerlegung in Linearfaktoren.
Binomische Formel anwenden.
Hast du eine Frage oder Feedback?
Die Gleichung hat die Lösungen –1 und –3.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Angabe der Nullstellen mit Hilfe der Faktorschreibweise:
Hast du eine Frage oder Feedback?
- 8
Löse die folgenden Gleichungen.
Gib im Eingabefeld die Lösung in der Form an, zum Beispiel "4;-1"
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
↓ Auf beiden Seiten radizieren. Dabei muss beachtet werden, dass die Ausdrücke auf beiden Seiten stets positiv sind. In diesem Fall ist das so.
↓ Beim Wurzelziehen den Betrag nicht vergessen!
Löse den Betrag auf. Dazu die beiden Fälle betrachten. Es gibt zwei Zahlen die, wenn sie in Betragstrichen stehen, 4 ergeben. Nämlich 4 und -4.
1. Fall
↓ Gleichung nach auflösen.
2. Fall
↓ Gleichung nach auflösen.
Antwort: Die Gleichung hat die beiden Lösungen 6 und -2. Die Lösungsmenge ist dann .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
↓ Auf beiden Seiten radizieren. Dabei muss beachtet werden, dass die Ausdrücke auf beiden Seiten stets positiv sind. In diesem Fall ist das so.
↓ Beim Wurzelziehen den Betrag nicht vergessen!
Den Betrag auflösen. Dazu die beiden Fälle betrachten. Es gibt zwei Zahlen die, wenn sie in Betragsstrichen stehen, 5 ergeben. Nämlich 5 und -5.
1. Fall
↓ Gleichung nach x auflösen
2. Fall
↓ Gleichung nach x auflösen
Antwort: Die Gleichung hat die beiden Lösungen 2 und -8. Die Lösungsmenge ist dann
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
↓ Auf beiden Seiten radizieren. Dabei muss beachtet werden, dass die Ausdrücke auf beiden Seiten stets positiv sind. In diesem Fall ist das so.
↓ Beim Wurzelziehen den Betrag nicht vergessen!
Den Betrag auflösen. Dazu die beiden Fälle betrachten. Es gibt zwei Zahlen die, wenn sie in Betragsstrichen stehen, 6 ergeben. Nämlich 6 und -6.
1. Fall
↓ Gleichung nach auflösen.
2. Fall
↓ Gleichung nach auflösen.
Antwort: Die Gleichung hat die beiden Lösungen -2 und -14. Die Lösungsmenge ist dann
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
↓ Auf beiden Seiten radizieren. Dabei muss beachtet werden, dass die Ausdrücke auf beiden Seiten stets positiv sind. In diesem Fall ist das so.
↓ Beim Wurzelziehen den Betrag nicht vergessen!
Den Betrag auflösen. Dazu die beiden Fälle betrachten. Es gibt zwei Zahlen die, wenn sie in Betragsstrichen stehen, ergeben. Nämlich und .
1. Fall
↓ Gleichung nach auflösen.
2. Fall
↓ Gleichung nach auflösen.
Antwort: Die Gleichung hat die beiden Lösungen und . Die Lösungsmenge ist dann
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

