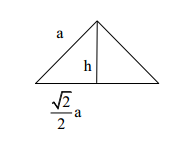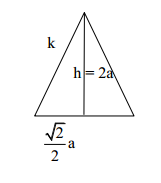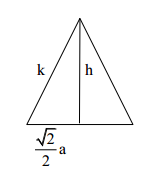Aufgaben zu Volumenberechnung

1
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
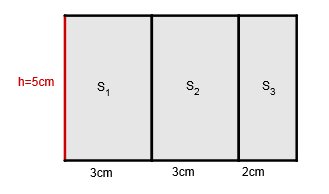
Ein rechteckiger Wasserbehälter mit den Maßen $0,8 m \cdot 0,45 m \cdot 1,5 m$ soll mit Wasser gefüllt werden.
Wie viel Liter kann er fassen?
l

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenberechnung beim Quader
$V_{Quader}$ $=$ $l \cdot b \cdot h$
↓
Setze die Werte ein
$=$ $0,8 m \cdot 0,45 m \cdot 1,5 m$
↓
Multipliziere
$=$ $0,54 m^{3}$
↓
Rechne $m^{3}$ in ${dm}^{3}$ um
$=$ $540 {dm}^{3}$
↓
Rechne ${dm}^{3}$ in Liter um
$=$ $540 l$
$\Rightarrow$ Der Wasserbehälter kann $540 l$ fassen.
2
Wie viel Brause passt in diese Riesenflasche?
An einem Hochhaus in der Chemnitzer Innenstadt wurde dieses Werbeplakat befestigt:
Diese "Riesenflasche" ist natürlich viel höher, breiter und tiefer als eine im Laden erhältliche Brauseflasche. Die Flasche aus dem Laden hat eine Höhe von ungefähr 23 cm und ein Volumen von 0,33 l.
Wie hoch unsere Riesenflasche ist, kannst du aus dem Bild ungefähr abschätzen. Vielleicht schaffst du das auch ohne Hilfe.
Berechne nun das ungefähre Volumen an Fassbrause in unserer Riesenflasche. Beachte dabei, dass es sich sowohl bei der Riesenflasche, als auch bei der kleinen Fasche um Körper handelt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenberechnung
Wir wandeln zunächst die Höhe der kleinen Flasche in die Einheit Meter um, damit beide Höhen die gleiche Einheit haben.
$23 c m = 0,23 m$
Nun dividieren wir die Höhe der Riesenflasche durch die Höhe der kleinen Flasche.
$24 m : 0,23 m = 104$
Da wir die Größe nur durch Abschätzen ermittelt haben, können wir unser Zwischenergebnis auch noch stärker runden. Unsere Riesenflasche ist also ungefähr 100 mal so hoch, wie eine kleine Brauseflasche.
Da es sich um Körper handelt, ist das Volumen der Riesnflasche demzufolge
$100 \cdot 100 \cdot 100 = 1000000$
mal so groß, wie das Volumen der kleinen Flasche.
Die Riesenflasche enthält also
$1000000 \cdot 0,33 l = 330000 l$
Da wir die Maße teilweise abgeschätzt haben und wir außerdem in der Zwischenrechnung bereits stark gerundet haben, runden wir das Endergebnis ebenfalls nochmals.
Antwortsatz:
Die Riesenflasche würde ungefähr 330.000 Liter Brause enthalten.
3
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
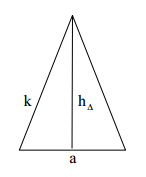
Eine gerade Pyramide hat als Grundfläche ein Rechteck mit den Seitenlängen $a$ und $b = 2 a$ . Die Höhe der Pyramide beträgt $h = 1,5 a$ .
Berechne die Kantenlängen als Vielfache von $a$ .
Berechne den Oberflächeninhalt der Pyramide in Vielfachen von $a^{2}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Berechnung der Länge der Diagonalen $d$
Bestimme die Länge der Diagonalen $d$ des Rechtecks mit dem Satz des Pythagoras.
$d^{2}$ $=$ $a^{2} + {(2 a)}^{2}$
$d^{2}$ $=$ $5 a^{2}$ $\sqrt{}$
↓
Ziehe die Wurzel.
$d$ $=$ $\pm \sqrt{5} a$
Das negative Ergebnis kannst du vernachlässigen, da Längen nur positiv sein können $\Rightarrow d = \sqrt{5} a$
Berechnung der Kantenlänge $k$
Berechne die Länge der Kante $k$ mit dem Satz des Pythagoras.
$k^{2}$ $=$ $h^{2} + {(\frac{d}{2})}^{2}$
↓
Setze $d = \sqrt{5} a$ und $h = 1,5 a$ ein.
$k^{2}$ $=$ ${(\frac{3}{2} a)}^{2} + {(\frac{\sqrt{5}}{2} a)}^{2}$
↓
Vereinfache.
$k^{2}$ $=$ $\frac{14}{4} a^{2}$ $\sqrt{}$
$k$ $=$ $\pm \frac{\sqrt{14}}{2} a$
Das negative Ergebnis kannst du wieder vernachlässigen, da Längen nur positiv sein können $\Rightarrow k = \frac{\sqrt{14}}{2} a$
Bestimmung des Oberflächeninhalts der Pyramide
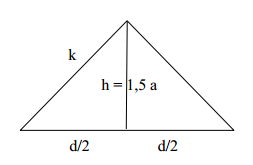
Die Oberfläche der Pyramide $O_{Pyramide}$ besteht aus der Fläche der Grundfläche $G$ und der Mantelfläche $M$ . Die Grundfläche $G$ ist ein Rechteck. Die Mantelfläche $M$ besteht aus 4 Dreiecksflächen, von denen je 2 der Dreicksflächen (und zwar die Gegenüberliegenden) gleich groß sind. Hier sind die Dreicksflächen als $m_{1}$ und $m_{2}$ bezeichnet.
$\begin{array}{rcllc} O_{Pyramide} & = & G & + & M \\ = & G & + & 2 \cdot m_{1} + 2 \cdot m_{2} \end{array}$
Bestimme erstmal die Grundfläche $G$ .
$\begin{array}{l} G = b \cdot a \\ = 2 a \cdot a \\ = 2 a^{2} \end{array}$
Um die Mantelfläche zu bestimmen benötigst du die Höhen der Dreiecksflächen. Sie heißen hier $h_{1}$ und $h_{2}$ . Bestimme $h_{1}$ und $h_{2}$ mit dem Satz des Pythagoras.
$h_{1}^{2} + {(\frac{a}{2})}^{2}$ $=$ $k^{2}$ $- {(\frac{a}{2})}^{2}$
$h_{1}^{2}$ $=$ $k^{2} - {(\frac{a}{2})}^{2}$
$h_{1}^{2}$ $=$ $\frac{14}{4} a^{2} - \frac{1}{4} a^{2}$
$h_{1}^{2}$ $=$ $\frac{13}{4} a^{2}$ $\sqrt{}$
$h_{1}$ $=$ $\pm \frac{\sqrt{13}}{2} a$
Da Längen nur positiv sein können, kannst du das negative Ergebnis vernachlässigen $\Rightarrow h_{1} = \frac{\sqrt{13}}{2} a$
$h_{2}^{2} + a^{2}$ $=$ $k^{2}$ $- a^{2}$
$h_{2}^{2}$ $=$ $k^{2} - a^{2}$
$h_{2}^{2}$ $=$ $\frac{14}{4} a^{2} - a^{2}$
$h_{2}^{2}$ $=$ $\frac{10}{4} a^{2}$ $\sqrt{}$
$h_{2}$ $=$ $\pm \frac{\sqrt{10}}{2} a$
Da Längen nur positiv sein können, kannst du das negative Ergebnis vernachlässigen $\Rightarrow h_{2} = \frac{\sqrt{10}}{2} a$
Jetzt kannst du die Dreiecksflächen berechnen.
$\begin{array}{l} m_{1} = \frac{1}{2} \cdot a \cdot h_{1} \\ = \frac{1}{2} \cdot a \cdot \frac{\sqrt{13}}{2} a \\ = \frac{\sqrt{13}}{4} a^{2} \end{array}$
$\begin{array}{l} m_{2} = \frac{1}{2} \cdot b \cdot h_{2} \\ = \frac{1}{2} \cdot 2 a \cdot \frac{\sqrt{10}}{2} a \\ = \frac{\sqrt{10}}{2} a^{2} \end{array}$
Jetzt lässt sich die Oberfläche bestimmen.
$\begin{array}{rcl} O_{Pyramide} & = & G + 2 \cdot m_{1} + 2 \cdot m_{2} \\ = & 2 a^{2} + 2 \cdot \frac{\sqrt{13}}{4} a^{2} + 2 \cdot \frac{\sqrt{10}}{2} a^{2} \\ = & (2 + \frac{\sqrt{13}}{2} + \sqrt{10}) a^{2} \\ \approx & 6,97 a^{2} \end{array}$
Der Oberflächeninhalt der Pyramide beträgt in etwa $6,97 a^{2}$ .
4
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Eine gerade Pyramide hat als Grundfläche ein gleichseitiges Dreieck mit der Kantenlänge a. Die Höhe der Pyramide beträgt 2a. Berechne die Seitenkantenlängen in Vielfachen von a. Berechne den Oberflächeninhalt der Pyramide in Vielfachen von a.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tetraeder
Die Seitenkantenlänge $k$
Im gleichseitigen Dreieck gilt mit Pythagoras:
$h_{a} = \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = \sqrt{\frac{3 \cdot a^{2}}{4}} = \frac{\sqrt{3}}{2} a$
$A_{Δ_{G}} = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot a \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} \cdot a^{2}$
Betrachte das Dreieck $A D S$ .
Die Seite $A D$ ist die Höhe des gleichseitigen Dreiecks $A B C$ .
Die Seitenhalbierenden (Höhen) schneiden sich im Verhältnis $2 : 1$ .
Für die Strecke $p$ gilt dann:
$p = \frac{2}{3} \cdot A D = \frac{2}{3} \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{3} a$
Für $q$ gilt: $q = \frac{1}{3} \cdot A D = \frac{1}{3} \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{6} a$
Im rechtwinkligen Dreieck $A H S$ ist
$h_{P} = 2 a$ . Dann gilt wieder mit Pythagoras:
$k^{2} = p^{2} + h_{P}^{2} = {(\frac{\sqrt{3}}{3} a)}^{2} + (2 a)^{2}$
$k^{2} = \frac{1}{3} a^{2} + 4 a^{2} = \frac{13}{3} a^{2}$
$\Rightarrow k = \sqrt{\frac{13}{3}} a = \frac{\sqrt{39}}{3} a$
Die Seitenkantenlänge $k$ ist:
$k = \frac{\sqrt{39}}{3} a$
Im rechtwinkligen Dreieck $H D S$ gilt:
$h_{Δ}^{2} = h_{P}^{2} + q^{2} = (2 a)^{2} + {(\frac{\sqrt{3}}{6} a)}^{2} = 4 a^{2} + \frac{1}{12} a^{2} = \frac{49}{12} a^{2}$
$\Rightarrow h_{Δ} = \frac{\sqrt{49}}{\sqrt{12}} a = \frac{7}{2 \sqrt{3}} a = \frac{7 \cdot \sqrt{3}}{6} a$
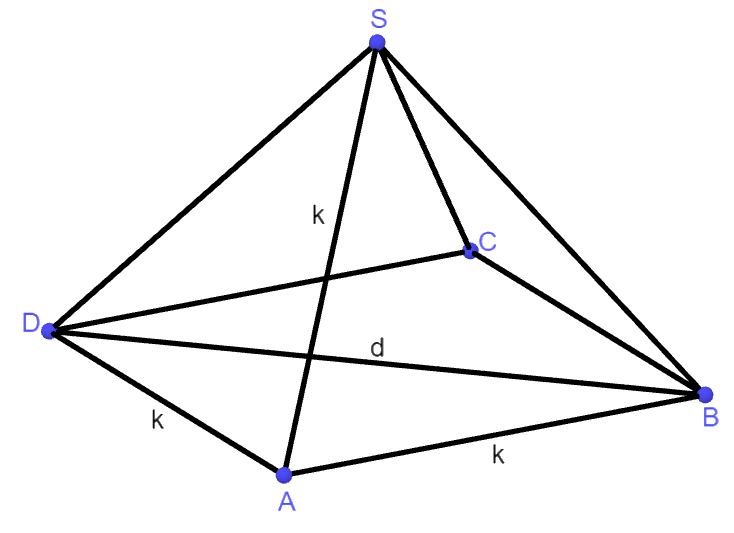
Der Oberflächeninhalt der Pyramide:
$O_{P} = A_{Δ_{G}} + 3 \cdot A_{Seitenfläche}$
$O_{P} = \frac{\sqrt{3}}{4} \cdot a^{2} + 3 \cdot \frac{1}{2} \cdot a \cdot \frac{7 \cdot \sqrt{3}}{6} a = \frac{\sqrt{3}}{4} \cdot a^{2} + \frac{7 \cdot \sqrt{3}}{4} a^{2} = \frac{8 \cdot \sqrt{3}}{4} a^{2} = 2 \sqrt{3} a^{2}$
Der Oberflächeninhalt der Pyramide ist gleich:
$O_{P} = 2 \sqrt{3} a^{2}$
5
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
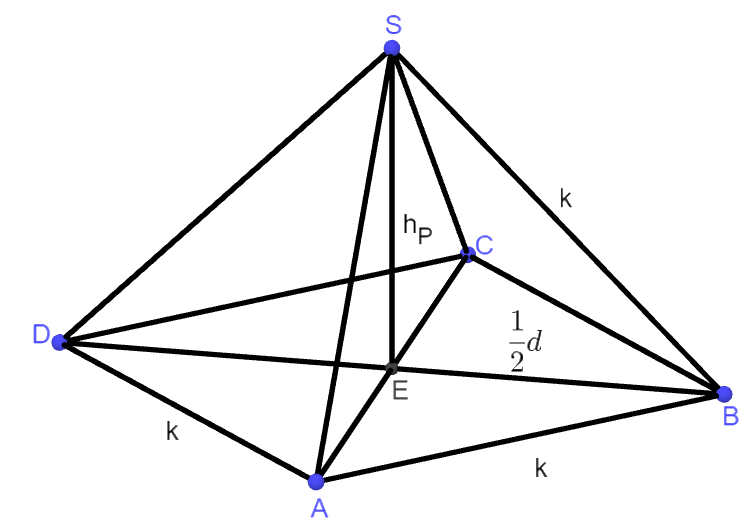
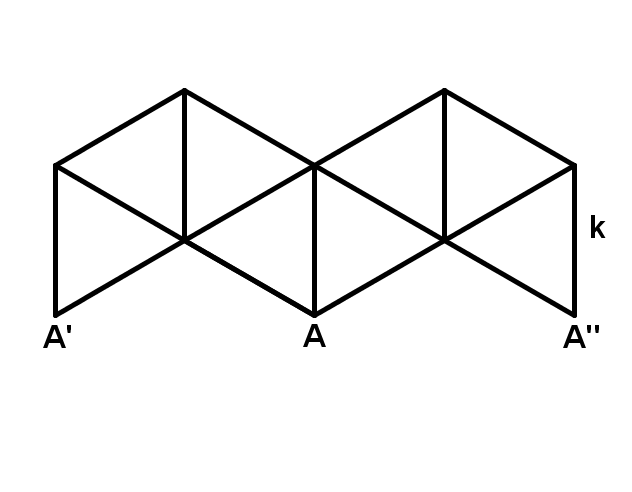
Das nebenstehende Netz mit lauter gleichseitigen Dreiecken mit Seitenlänge k lässt sich zu einem Oktaeder falten, indem man zunächst aus der "linken" Hälfte des Netzes eine Pyramide herstellt.
Berechne die Höhe dieser Pyramide und zeichne ein Schrägbild des Oktaeders.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Aus dem halben Netz wird eine Pyramide hergestellt.
Die Diagonale $d$ der Grundfläche dieser Pyramide wird mit dem Satz des Pythagoras berechnet:
$d = \sqrt{2 k^{2}} = \sqrt{2} k$
Gesucht ist die Höhe $h_{P}$ der Pyramide.
Im Dreieck $E B S$ gilt mit Pythagoras:
$h_{P} = \sqrt{k^{2} - {(\frac{d}{2})}^{2}}$
$h_{P} = \sqrt{k^{2} - {(\frac{\sqrt{2}}{2} k)}^{2}} = \sqrt{\frac{1}{2} k^{2}}$
$h_{P} = \frac{\sqrt{2}}{2} k \approx 0,71 k$
Schrägbild des Oktaeders
Für die Zeichnung gilt: $q = 0,5$ und $α = 45^{\circ} .$
Konstruiere ein Parallelogramm $A B C D$ mit dem Diagonalenschnittpunkt $E$ .
Im Punkt $B$ wird die Seite $B C = \frac{1}{2} A B$ unter dem Winkel $45^{\circ}$ abgetragen.
Im Diagonalenschnittpunkt $E$ wird die Höhe $h_{P} = E S = 0,71 A B$ eingezeichnet.
Die Höhe der zweiten Pyramide $h_{P}^{'} = E S^{'} = 0,71 A B$ wird ebenfalls im Punkt E eingezeichnet. Zeichne dann die Strecken von $S$ zu $A, B, C$ und $D$ und von $S^{'}$ zu $A, B, C$ und $D$ .
6
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Die rechteckige Grundfläche eines Ölbehälters hat die Maße a=60cm und b=40cm.
Der Behälter ist mit V=140 Liter Öl gefüllt.
Welche Höhe h hat der Ölspiegel in ganzen cm?
cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen und Massenberechnung
$V$ $=$ $140 l$
↓
Volumen in $d m^{3}$ umrechnen
$V$ $=$ $140 d m^{3}$
↓
$d m^{3}$ in $c m^{3}$ umrechnen
$V$ $=$ $140000 c m^{3}$
$V$ $=$ $c \cdot b \cdot h$ $: (a \cdot b)$
$h$ $=$ $\frac{V}{a \cdot b}$
↓
a, b und V einsetzen
$h$ $=$ $\frac{140 000 c m^{3}}{60 c m \cdot 40 c m}$
↓
multiplizieren und dividieren
$h$ $=$ $58, 3 c m$
↓
auf eine ganze Stelle runden
$h$ $\approx$ $58 c m$
7
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Ein zylindrisches Ausdehnungsgefäß hat d=35 cm Durchmesser und h=450 mm Höhe.
Wie viel Liter fasst das Gefäß?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Gegeben:
Zylinder mit
Durchmesser $d = 35 cm$
Höhe $h = 450 mm$
Gesucht:
Volumen $V$ in Litern $(l)$
Lösung:
Lösungidee:
$V=?$
Da es sich bei dem Gefäß um einen Zylinder handelt, brauchst du die Formel für das Volumen eines Zylinders:
$V_{Z y l i n d e r} = G \cdot h = π \cdot r^{2} \cdot h$
$V_{Z y l i n d e r} = π \cdot r^{2} \cdot h$
Die Höhe $h$ ist gegeben, und den Radius $r$ kannst du aus dem Durchmesser $d$ berechnen.
Allerdings sollten, wenn du in die Formel einsetzt, $h$ und $r$ die gleiche Einheit haben.
Tipp: Wenn du $h$ und $r$ (oder $d$ ) schon jetzt beide in $dm$ umwandelst, kommt das Volumen in ${dm}^{3}$ (= in Litern $l$ ) heraus. Andernfalls musst du eben nachher die Volumeneinheit noch umrechnen.
Umrechnen, Einsetzen der Zahlen und Ausrechnen:
$h = 450 mm = 4,5 dm$
$d = 35 cm = 3,5 dm$
Aus dem Durchmesser $d$ berechnest du dann den Radius $r$ ,
$r = \frac{d}{2} = 1,75 dm$
… und setzt $r$ und $h$ in die Volumenformel ein:
$V = π \cdot {(1,75 dm)}^{2} \cdot 4,5 dm$
Das rechnest du aus und rundest das Ergebnis.
$V \approx 43,3 {dm}^{3}$
${dm}^{3}$ sind dasselbe wie Liter.
Wenn du mit anderen Einheiten gerechnet hast (was natürlich auch möglich ist), musst du dein Ergebnis jetzt noch umrechnen .
$V \approx 43,3 l$
8
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Berechne Volumen und Oberfläche, wenn der Körper jeweils die Höhe $h = 5 cm$ hat:
1. Prisma mit gleichschenkligem Dreieck als Grundfläche, Schenkellänge $3 cm$ und Basis $2 cm$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prisma
  $\begin{array}{l} V_{Prisma} = G \cdot h \\ = A_{Dreieck} \cdot h \end{array}$
  Allgemeine Volumenformel für Prismen auf gegebenes Prisma anwenden, indem man den Flächeninhalt des gleichschenkligen Dreiecks für die Grundfläche einsetzt.
  Allgemeine Flächenformel des Dreiecks.
  $\begin{array}{l} A_{Dreieck} = \frac{1}{2} \cdot Basis \cdot h_{Dreieck} \end{array}$
  Die Höhe des Dreiecks $h_{Dreieck}$ kann mit Hilfe des Satzes des Pythagoras berechnet werden.
  $\begin{array}{l} (h_{Dreieck})^{2} = {(3 cm)}^{2} - {(1 cm)}^{2} \\ \Leftrightarrow h_{Dreieck} = \sqrt{8 {cm}^{2}} = \sqrt{8} cm \end{array}$
  Einsetzen der bekannten Seitenlängen in die Gleichung für $A_{Dreieck}$
  $\begin{array}{l} \begin{array}{l} A_{Dreieck} = \frac{1}{2} \cdot 2 c m \cdot \sqrt{8} cm \end{array} \\ = \sqrt{8} {cm}^{2} \end{array}$
  Einsetzen in die Volumenformel des Prismas
  $\begin{array}{l} \begin{array}{l} V_{Prisma} = \sqrt{8} {cm}^{2} \cdot 5 cm \\ = 5 \sqrt{8} {cm}^{3} \end{array} \\ \approx 14,14 {cm}^{3} \end{array}$
  Oberflächeninhalt
  $O_{\Pr i s m a} = 2 \cdot G + M$
  Allgemeine Oberflächenformel für Prismen auf gegebenes Prisma anwenden, indem die man die Flächeninhalte der rechteckigen Seitenflächen addiert und für die Mantelfläche $M$ einsetzt.
  $\begin{array}{l} O_{Prisma} = 2 \cdot A_{Dreieck} + S_{1} + S_{2} + S_{3} \\ = 2 \cdot \sqrt{8} {cm}^{2} + (3 cm \cdot 5 cm) + (3 cm \cdot 5 cm) + (2 cm \cdot 5 cm) \\ = 2 \sqrt{8} {cm}^{2} + 40 {cm}^{2} \\ \approx 45,66 {cm}^{2} \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zylinder mit Radius $r = 3 cm$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenformeln
  Das Volumen eine Zylinders berechen wir mit
  $V = r^{2} \cdot π \cdot h$
  Mit $r = 3$ und $h = 5$ ist
  $V = 3^{2} \cdot π \cdot 5 c m^{3} = 45 π c m^{3} \approx 141,37 c m^{3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Gerade Pyramide (alle Seitenkanten gleich lang) mit Quadrat der Kantenlänge $24 cm$ als Grundfläche.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenformeln
  Bei jeder Pyramide gilt $V = \frac{1}{3} G \cdot h$ .
  Da die Grundfläche ein Quadrat mit Kantenlänge $24 c m$ ist, ist
  $G = 24^{2} c m^{2}$ und
  $V = \frac{1}{3} 24^{2} \cdot 5 c m^{3} = 960 c m^{3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Kegel mit Radius $r = 3 cm$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenformeln
  Für das Kegelvolumen gilt
  $V = \frac{1}{3} r^{2} \cdot π \cdot h$
  Mit $r = 3 c m$ und $h = 5 c m$ ist
  $V = \frac{1}{3} \cdot 9 \cdot π \cdot 5 c m^{3} = 15 π c m^{3} \approx 42,12 c m^{3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
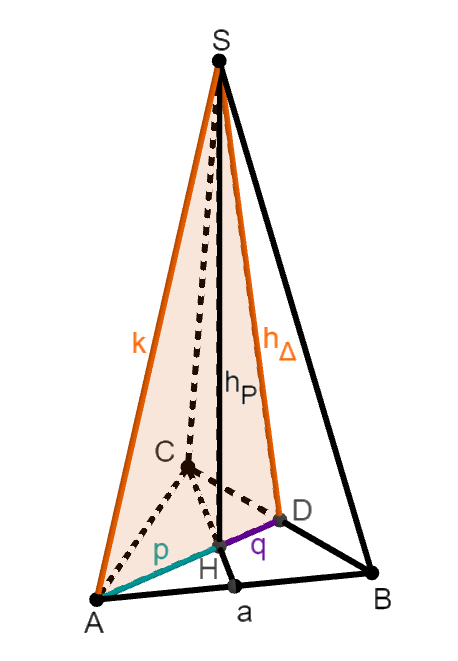
Das Bild zeigt eine gerade Pyramide mit einem Quadrat als Grundfläche. Der Punkt $C$ halbiert die Höhe $h$ .
Die Winkel im Dreieck $A B C$ hängen nicht von $a$ ab.
Berechne jeweils in Abhängigkeit von $a$
1. Das Volumen der Pyramide
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Die Diagonalenlänge der Grundfläche ist $d = \sqrt{2} a$ .
  Der Mittelpunkt der Diagonalen ist $M$ .
  Dann gilt im Dreieck $A M S$ mit dem Satz des Pythagoras:
  $h^{2} = (3 a)^{2} - {(\frac{d}{2})}^{2}$
  $h^{2} = 9 a^{2} - {(\frac{\sqrt{2} a}{2})}^{2}$
  $\Rightarrow h = \sqrt{9 a^{2} - \frac{1}{2} a^{2}} = \frac{\sqrt{34}}{2} a$
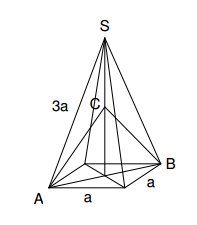
  Damit kann nun das Volumen der Pyramide berechnet werden:
  $V = \frac{1}{3} \cdot G \cdot h$
  $V = \frac{1}{3} \cdot a^{2} \cdot \frac{\sqrt{34}}{2} a = \frac{\sqrt{34}}{6} a^{3} \approx 0,972 a^{3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Den Oberflächeninhalt der Pyramide
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Für den Oberflächeninhalt muss die Fläche der Pyramidendreiecke berechnet werden.
  Im gezeichneten Dreieck ist die Dreiecksgrundseite die halbe Dreiecksseite $a$ .
  Im Dreieck gilt dann mit dem Satz des Pythagoras:
  $h_{Δ} = \sqrt{(3 a)^{2} - {(\frac{a}{2})}^{2}} = \sqrt{9 a^{2} - \frac{a^{2}}{4}}$
  $h_{Δ} = \frac{\sqrt{35}}{2} a$
  Für den Oberflächeninhalt folgt dann:
  $O = G + 4 \cdot A_{Δ} = G + 4 \cdot \frac{1}{2} \cdot a \cdot h_{Δ}$
  $O = a^{2} + 4 \cdot \frac{1}{2} \cdot a \cdot \frac{\sqrt{35}}{2} \cdot a$
  $O = a^{2} + \sqrt{35} \cdot a^{2} = (1 + \sqrt{35}) \cdot a^{2}$
  $O \approx 6,916 a^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Die drei Seitenlängen im Dreieck $A B C$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
  Die Länge der Dreiecksseite $[A B]$ ist die Diagonalenlänge $d = \sqrt{2} a$ .
  Die Höhe $h$ in diesem Dreieck ist die halbe Pyramidenhöhe.
  $\Rightarrow h = \frac{1}{2} \frac{\sqrt{34}}{2} a = \frac{\sqrt{34}}{4} a$
  Die Längen der beiden Seiten $[A C]$ und $[B C]$ sind gleich groß. Die Länge wird wieder mit dem Satz des Pythagoras berechnet:
  $A C = B C = \sqrt{h^{2} + {(\frac{d}{2})}^{2}} = \sqrt{{(\frac{\sqrt{34}}{4} a)}^{2} + {(\frac{\sqrt{2} a}{2})}^{2}}$
  $A C = B C = \sqrt{\frac{34}{16} a^{2} + \frac{1}{2} a^{2}} = \frac{\sqrt{42}}{4} a$
  Ergebnis: $A C = B C = \frac{\sqrt{42}}{4} a$ und $A B = \sqrt{2} a$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Die Winkel im Dreieck $A B C$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Funktionen
  Im linken Dreieck gilt:
  $\tan α = \frac{h}{\frac{d}{2}} = \frac{2 \cdot h}{d}$
  $\tan α = \frac{2 \cdot \frac{\sqrt{34}}{4} a}{\sqrt{2} a}$
  $\tan α = \frac{\sqrt{34}}{2 \cdot \sqrt{2}}$
  $\Rightarrow α = \tan^{- 1} (\frac{\sqrt{34}}{2 \cdot \sqrt{2}}) \approx {64,12}^{\circ}$
  Der Winkel $A B C$ ist gleich dem Winkel $α$ .
  Der Winkel $A C B = 180^{\circ} - 2 \cdot α = 180^{\circ} - {128,24}^{\circ} = {51,56}^{\circ}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Den Flächeninhalt des Dreiecks $A B C$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
  $A = \frac{1}{2} \cdot d \cdot h$
  $A = \frac{1}{2} \cdot \sqrt{2} a \cdot \frac{\sqrt{34}}{4} a = \frac{\sqrt{17}}{4} a^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Ein Kegel, dessen Höhe $h$ so groß ist wie der Grundkreis-Durchmesser, habe das Volumen $1 L i t e r$ .
1. Berechne $h$ .
  
  Lösung zur 1. Frage der Aufgabe:
  gegeben:
  Grundkreisdurchmesser des Kreiskegels $d=h$
  Volumen $V = 1 l$
  gesucht:
  Höhe des Kreiskegels $h$
  Darstellen des Grundkreisradius mit $h$
  Um die Höhe $h$ zu berechnen, kannst du zuerst den Radius $r$ als $h$ geteilt durch zwei darstellen, denn $d$ gleicht $h$ und ist außerdem doppelt so lang wie $r$ .
  $r= \frac{d}{2}$
  $r = \frac{h}{2}$
  Aufstellen eines Gleichungssystemes:
  $r = \frac{h}{2}$ ein Gleichungssystem mit zwei Gleichungen auf.
  Gleichung (I) ist die Darstellung von $r$ mit $h$ .
  Gleichung (II) ist die Formel für die Berechnung des Volumens von einem Kreiskegel mit den eingesetzten Wert von $r= \frac{h}{2}$
  (I): $r= \frac{h}{2}$
  (II): $\frac{1}{3} \cdot r^{2} \cdot π \cdot h = 1 l$
  Nun löst du das Gleichungssystem mit dem Einsetzungsverfahren, wobei du die Gleichung (I) ind (II) einsetzst.
  (I) in (II):
  $\frac{1}{3} \cdot \frac{h^{2}}{2^{2}} \cdot π \cdot h = 1 l$
  $\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$ $=$ $1 l$
  $\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$ $=$ $1 l$ $\cdot 12$
  $h^{3} \cdot π$ $=$ $12 \cdot 1 l$
  $h^{3} \cdot π$ $=$ $12 l$ $: π$
  $h^{3}$ $=$ $\frac{12 l}{π}$ $\sqrt[3]{}$
  $h$ $=$ $\sqrt[3]{\frac{12 l}{π}}$
  $=$ $\sqrt[3]{\frac{12 {dm}^{3}}{π}}$
  $=$ $1,563185283593544 dm$
  $\approx$ $1,56 dm$
  Du kannst $r$ ausrechnen, indem du $h$ in Gleichung (I) einsetzst. Du benötigst den Radius $r$ , um die 2 Frage der Aufgabenstellung zu beantworten.
  $h$ in (I):
  $r = \frac{1,56 dm}{2} = 0,78 dm$
  Antwort zur 1. Frage der Aufgabe:
  Der Kreiskegel ist etwa $1,56 d m$ hoch.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne nun den Mittelpunktswinkel $α$ des Sektors, aus dem dieser Kegel gefertigt werden kann
  
  Lösung zur 2. Frage der Aufgabe:
  Berechnung der Mantellinie s:
  Um den Mittelpunktswinkel α des Kreissektors, aus dem der Kegel gefertigt werden kann, zu bestimmen, musst du zuerst die Mantellinie $s$ des Kegels ausrechnen. Du musst dazu dir ein rechtwinkliges Dreieck vorstellen, welches den Grundkreismittelpunkt, irgendeinen Punkt auf der Kreislinie der Höhe und die Spitze des Kreiskegels verbindet. Der Grundkreismittelpunkt und der Punkt auf der Kreislinie verbinden sich zu einer Kathete und dem Grundkreisradius r. Der Punkt auf der Kreislinie verbindet sich mit der Kegelspitze zur Hypotenuse und der Mantellinie s. Die Kegelspitze verbindet sich mit dem Grundkreismittelpunkt zu der zweiten Kathete und der Höhe h. Da h und r bereits bekannt sind, kannst du s mit dem Satz des Pythagoras berechnen.
  $s^{2}$ $=$ $h^{2} + r^{2}$
  $=$ ${1,56}^{2} {dm}^{2} + {0,78}^{2} {dm}^{2}$
  $=$ $3,042 {dm}^{2}$ $\sqrt{}$
  $s$ $=$ $\sqrt{3,042 {dm}^{2}}$
  $\approx$ $1,74 dm$
  Anmerkung:
  Die Lösungen der Gleichung wären:
  $s_{1 / 2} = \pm \sqrt{3,042 {dm}^{2}}$
  Da s eine Länge ist, wäre eine negative Lösung nicht sinnvoll, weshalb du diese nicht weiter beachten musst.
  Berechnung des Mittelpunktswinkels $α$
  Nun kannst du $α$ berechnen, indem du dir bereits bekannte Werte in eine nach $α$ umgeformte Version von dieser Formel
  $\frac{α}{360^{\circ}} = \frac{2 \cdot π \cdot r}{2 \cdot π \cdot s} = \frac{r}{s}$
  einsetzst.
  $\frac{α}{360^{\circ}} = \frac{0,78 dm}{1,74 dm} | \cdot 360^{\circ}$
  Du multiplizierst auf beiden Seiten der Gleichung mit $360 °$ .
  $α = 0,45 \cdot 360^{\circ} = 162^{\circ}$
  Antwort:
  Der Mittelpunktswinkel α des Sektors, aus dem der Kegel gefertigt werden kann, ist $162 °$ groß.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
11
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
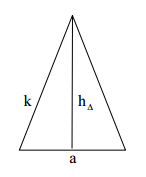
Das Bild zeigt eine gerade Pyramide mit einem Quadrat der Kantenlänge $a$ als Grundfläche. Die Seitenkanten haben ebenfalls die Länge $a$ .
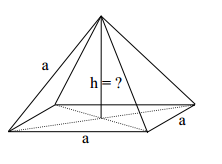
1. Zeichne ein Netz der Pyramide für $a = 4 cm$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Teilaufgabe a
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne die Höhe $h$ der Pyramide in Vielfachen von $a$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Teilaufgabe b
  Satz des Pythagoras anwenden
  $h^{2} + {(\frac{\sqrt{2}}{2} a)}^{2} = a^{2} \Rightarrow h = \frac{\sqrt{2}}{2} a$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Berechne den Oberflächeninhalt $O$ der Pyramide
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Teilaufgabe c
  Die Höhe innerhalb der Dreiecks-Seitenfläche bestimmen. Satz des Pythagoras anwenden.
  ${(h_{△})}^{2} + {(\frac{1}{2} a)}^{2} = a^{2} \Rightarrow h_{△} = \frac{\sqrt{3}}{2} a$
  Flächeninhalt des Dreiecks bestimmen:
  $A_{△} = \frac{1}{2} \cdot a \cdot h_{△} = \frac{\sqrt{3}}{4} a^{2}$
  Oberflächeninhalt bestimmen:
  $O = 4 \cdot A_{△} + a^{2} = a^{2} + 4 \cdot \frac{\sqrt{3}}{4} a^{2} = (1 + \sqrt{3}) \cdot a^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
12
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
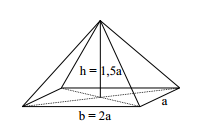
Das Bild zeigt eine gerade Pyramide mit einem Quadrat der Kantenlänge $a$ als Grundfläche. Die Höhe der Pyramide ist $2 a$ .
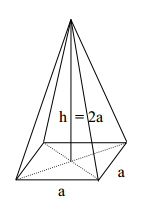
1. Berechne die Länge der Seitenkanten $k$ in Vielfachen von $a$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Teilaufgabe 1
  Diagonale $d$ des Quadrats mit dem Satz des Pythagoras berechnen.
  $d$ $=$ $\sqrt{2 a^{2}}$
  $d$ $=$ $\sqrt{2} a$
  Seitenkante $k$ mit Pythagoras berechnen:
  ${(2 a)}^{2} + {(\frac{\sqrt{2}}{2} a)}^{2}$ $=$ $k^{2}$
  $k$ $=$ $\frac{3 \sqrt{2}}{2} a$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne den Oberflächeninhalt $O$ der Pyramide in Vielfachen von $a^{2}$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Teilaufgabe 2
  Höhe $h_{△}$ im Dreieck mit Satz des Pythagoras berechnen:
  $k^{2}$ $=$ $h_{Δ}^{2} + {(\frac{a}{2})}^{2}$ $- {(\frac{a}{2})}^{2}$
  $h_{Δ}$ $=$ $\sqrt{k^{2} - {(\frac{a}{2})}^{2}}$
  $h_{Δ}$ $=$ $\frac{\sqrt{17}}{2} a$
  Fläche des Dreiecks berechnen:
  $A_{Δ}$ $=$ $\frac{1}{2} \cdot a \cdot h_{Δ}$
  $=$ $\frac{\sqrt{17}}{4} a^{2}$
  Oberfläche der Pyramide berechnen:
  $O$ $=$ $a^{2} + 4 \cdot A_{Δ}$
  $=$ $a^{2} + \sqrt{17} a^{2}$
  $=$ $(1 + \sqrt{17}) a^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Bestimme $a$ auf Millimeter genau, wenn der Oberflächeninhalt genau $400 {cm}^{2}$ betragen soll.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Teilaufgabe 3
  $S$ $=$ $400 {cm}^{2}$
  ↓
  Oberfläche gleichsetzen.
  $(1 + \sqrt{17}) a^{2}$ $=$ $400 {cm}^{2}$ $: (1 + \sqrt{17})$
  ↓
  Gleichung umformen.
  $a^{2}$ $=$ $\frac{400 {cm}^{2}}{(1 + \sqrt{17})}$
  ↓
  Gleichung umformen.
  $a$ $=$ $\frac{\sqrt{400 {cm}^{2}}}{\sqrt{1 + \sqrt{17}}}$
  $a$ $=$ $8,8 cm$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
13
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Ein Würfel und eine gerade Pyramide haben jeweils ein Quadrat der Kantenlänge $a$ als Grundfläche. Beide Körper sollen den gleichen Oberflächeninhalt haben.
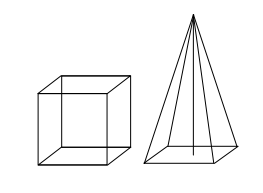
1. Wie lang müssen dann die Seitenkanten der Pyramide sein?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grundkörper
  Würfel und Pyramide
  Gleichsetzung des Oberflächeninhalts des Würfels und der Pyramide:
  $6 a^{2}$ $=$ $a^{2} + 4 \cdot A_{Δ}$ $- a^{2}$
  $5 a^{2}$ $=$ $4 \cdot A_{Δ}$
  ↓
  Formel für Flächeninhalt eines Dreiecks für $A_{△}$ einsetzen.
  $5 a^{2}$ $=$ $2 \cdot a \cdot h_{Δ}$ $: 2 a$
  $\frac{5}{2} a$ $=$ $h_{Δ}$
  Die Höhe des Dreiecks beträgt $h_{Δ} = \frac{5}{2} a$ .
  Um $k$ zu berechnen, wende den Satz des Pythagoras an:
  $k^{2}$ $=$ $h_{Δ}^{2} + {(\frac{1}{2} a)}^{2}$
  $k^{2}$ $=$ $\frac{25}{4} a^{2} + \frac{1}{4} a^{2}$
  $k^{2}$ $=$ $\frac{26}{4} a^{2}$ $\sqrt{}$
  $k$ $=$ $\frac{\sqrt{26}}{2} a$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne auch die Höhe der Pyramide.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grundkörper
  Diagonale $d$ des Quadrats mit Satz des Pythagoras bestimmen:
  $d$ $=$ $\sqrt{2 a^{2}}$
  $d$ $=$ $\sqrt{2} a$
  Um $h$ zu berechnen, wende den Satz des Pythagoras an:
  $k^{2}$ $=$ $h^{2} + {(\frac{d}{2})}^{2}$ $- {(\frac{d}{2})}^{2}$
  $h^{2}$ $=$ $k^{2} - {(\frac{d}{2})}^{2}$
  $h^{2}$ $=$ $\frac{26}{4} a^{2} - {(\frac{\sqrt{2}}{2} a)}^{2}$
  $h^{2}$ $=$ $\frac{26}{4} a^{2} - \frac{2}{4} a^{2}$
  $h^{2}$ $=$ $\frac{24}{4} a^{2}$
  $h^{2}$ $=$ $6 a^{2}$ $\sqrt{}$
  $h$ $=$ $\sqrt{6} a$
  $h$ $\approx$ $2,45 a$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
14
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Das Bild zeigt eine gerade Pyramide mit einem Quadrat als Grundfläche. Der Punkt $C$ halbiert die Höhe $h$ .
Die Winkel im Dreieck $A B C$ hängen nicht von $a$ ab.
Berechne jeweils in Abhängigkeit von $a .$
1. Das Volumen der Pyramide
2. Den Oberflächeninhalt der Pyramide
3. Die drei Seitenlängen im Dreieck $A B C$
4. Die Winkel im Dreieck $A B C$
5. Den Flächeninhalt des Dreiecks $A B C$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$V_{Quader}$	$=$	$l \cdot b \cdot h$
	↓	Setze die Werte ein
	$=$	$0,8 m \cdot 0,45 m \cdot 1,5 m$
	↓	Multipliziere
	$=$	$0,54 m^{3}$
	↓	Rechne $m^{3}$ in ${dm}^{3}$ um
	$=$	$540 {dm}^{3}$
	↓	Rechne ${dm}^{3}$ in Liter um
	$=$	$540 l$

$d^{2}$	$=$	$a^{2} + {(2 a)}^{2}$
$d^{2}$	$=$	$5 a^{2}$	$\sqrt{}$
	↓	Ziehe die Wurzel.
$d$	$=$	$\pm \sqrt{5} a$

$k^{2}$	$=$	$h^{2} + {(\frac{d}{2})}^{2}$
	↓	Setze $d = \sqrt{5} a$ und $h = 1,5 a$ ein.
$k^{2}$	$=$	${(\frac{3}{2} a)}^{2} + {(\frac{\sqrt{5}}{2} a)}^{2}$
	↓	Vereinfache.
$k^{2}$	$=$	$\frac{14}{4} a^{2}$	$\sqrt{}$
$k$	$=$	$\pm \frac{\sqrt{14}}{2} a$

$h_{1}^{2} + {(\frac{a}{2})}^{2}$	$=$	$k^{2}$	$- {(\frac{a}{2})}^{2}$
$h_{1}^{2}$	$=$	$k^{2} - {(\frac{a}{2})}^{2}$
$h_{1}^{2}$	$=$	$\frac{14}{4} a^{2} - \frac{1}{4} a^{2}$
$h_{1}^{2}$	$=$	$\frac{13}{4} a^{2}$	$\sqrt{}$
$h_{1}$	$=$	$\pm \frac{\sqrt{13}}{2} a$

$h_{2}^{2} + a^{2}$	$=$	$k^{2}$	$- a^{2}$
$h_{2}^{2}$	$=$	$k^{2} - a^{2}$
$h_{2}^{2}$	$=$	$\frac{14}{4} a^{2} - a^{2}$
$h_{2}^{2}$	$=$	$\frac{10}{4} a^{2}$	$\sqrt{}$
$h_{2}$	$=$	$\pm \frac{\sqrt{10}}{2} a$

$V$	$=$	$140 l$
	↓	Volumen in $d m^{3}$ umrechnen
$V$	$=$	$140 d m^{3}$
	↓	$d m^{3}$ in $c m^{3}$ umrechnen
$V$	$=$	$140000 c m^{3}$

$V$	$=$	$c \cdot b \cdot h$	$: (a \cdot b)$
$h$	$=$	$\frac{V}{a \cdot b}$
	↓	a, b und V einsetzen
$h$	$=$	$\frac{140 000 c m^{3}}{60 c m \cdot 40 c m}$
	↓	multiplizieren und dividieren
$h$	$=$	$58, 3 c m$
	↓	auf eine ganze Stelle runden
$h$	$\approx$	$58 c m$

$\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$	$=$	$1 l$
$\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$	$=$	$1 l$	$\cdot 12$
$h^{3} \cdot π$	$=$	$12 \cdot 1 l$
$h^{3} \cdot π$	$=$	$12 l$	$: π$
$h^{3}$	$=$	$\frac{12 l}{π}$	$\sqrt[3]{}$
$h$	$=$	$\sqrt[3]{\frac{12 l}{π}}$
	$=$	$\sqrt[3]{\frac{12 {dm}^{3}}{π}}$
	$=$	$1,563185283593544 dm$
	$\approx$	$1,56 dm$

$s^{2}$	$=$	$h^{2} + r^{2}$
	$=$	${1,56}^{2} {dm}^{2} + {0,78}^{2} {dm}^{2}$
	$=$	$3,042 {dm}^{2}$	$\sqrt{}$
$s$	$=$	$\sqrt{3,042 {dm}^{2}}$
	$\approx$	$1,74 dm$

${(2 a)}^{2} + {(\frac{\sqrt{2}}{2} a)}^{2}$	$=$	$k^{2}$
$k$	$=$	$\frac{3 \sqrt{2}}{2} a$

$k^{2}$	$=$	$h_{Δ}^{2} + {(\frac{a}{2})}^{2}$	$- {(\frac{a}{2})}^{2}$
$h_{Δ}$	$=$	$\sqrt{k^{2} - {(\frac{a}{2})}^{2}}$
$h_{Δ}$	$=$	$\frac{\sqrt{17}}{2} a$

$S$	$=$	$400 {cm}^{2}$
	↓	Oberfläche gleichsetzen.
$(1 + \sqrt{17}) a^{2}$	$=$	$400 {cm}^{2}$	$: (1 + \sqrt{17})$
	↓	Gleichung umformen.
$a^{2}$	$=$	$\frac{400 {cm}^{2}}{(1 + \sqrt{17})}$
	↓	Gleichung umformen.
$a$	$=$	$\frac{\sqrt{400 {cm}^{2}}}{\sqrt{1 + \sqrt{17}}}$
$a$	$=$	$8,8 cm$

$A_{Δ}$	$=$	$\frac{1}{2} \cdot a \cdot h_{Δ}$
	$=$	$\frac{\sqrt{17}}{4} a^{2}$

$O$	$=$	$a^{2} + 4 \cdot A_{Δ}$
	$=$	$a^{2} + \sqrt{17} a^{2}$
	$=$	$(1 + \sqrt{17}) a^{2}$

$6 a^{2}$	$=$	$a^{2} + 4 \cdot A_{Δ}$	$- a^{2}$
$5 a^{2}$	$=$	$4 \cdot A_{Δ}$
	↓	Formel für Flächeninhalt eines Dreiecks für $A_{△}$ einsetzen.
$5 a^{2}$	$=$	$2 \cdot a \cdot h_{Δ}$	$: 2 a$
$\frac{5}{2} a$	$=$	$h_{Δ}$

$k^{2}$	$=$	$h_{Δ}^{2} + {(\frac{1}{2} a)}^{2}$
$k^{2}$	$=$	$\frac{25}{4} a^{2} + \frac{1}{4} a^{2}$
$k^{2}$	$=$	$\frac{26}{4} a^{2}$	$\sqrt{}$
$k$	$=$	$\frac{\sqrt{26}}{2} a$

$k^{2}$	$=$	$h^{2} + {(\frac{d}{2})}^{2}$	$- {(\frac{d}{2})}^{2}$
$h^{2}$	$=$	$k^{2} - {(\frac{d}{2})}^{2}$
$h^{2}$	$=$	$\frac{26}{4} a^{2} - {(\frac{\sqrt{2}}{2} a)}^{2}$
$h^{2}$	$=$	$\frac{26}{4} a^{2} - \frac{2}{4} a^{2}$
$h^{2}$	$=$	$\frac{24}{4} a^{2}$
$h^{2}$	$=$	$6 a^{2}$	$\sqrt{}$
$h$	$=$	$\sqrt{6} a$
$h$	$\approx$	$2,45 a$

Aufgaben zu Volumenberechnung

Berechnung der Länge der Diagonalen d

Berechnung der Kantenlänge k

Bestimmung des Oberflächeninhalts der Pyramide

Die Seitenkantenlänge k

Der Oberflächeninhalt der Pyramide:

Schrägbild des Oktaeders

Lösung:

Lösungidee:

Umrechnen, Einsetzen der Zahlen und Ausrechnen:

Oberflächeninhalt

OPr⁡isma=2⋅G+M

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung zur 1. Frage der Aufgabe:

Antwort zur 1. Frage der Aufgabe:

Hast du eine Frage oder Feedback?

Lösung zur 2. Frage der Aufgabe:

Berechnung der Mantellinie s:

Anmerkung:

Berechnung des Mittelpunktswinkels α

Antwort:

Hast du eine Frage oder Feedback?

Teilaufgabe a

Hast du eine Frage oder Feedback?

Teilaufgabe b

Hast du eine Frage oder Feedback?

Teilaufgabe c

Hast du eine Frage oder Feedback?

Teilaufgabe 1

Hast du eine Frage oder Feedback?

Teilaufgabe 2

Hast du eine Frage oder Feedback?

Teilaufgabe 3

Hast du eine Frage oder Feedback?

Würfel und Pyramide

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung der Länge der Diagonalen $d$

Berechnung der Kantenlänge $k$

Die Seitenkantenlänge $k$

$O_{\Pr i s m a} = 2 \cdot G + M$

Berechnung des Mittelpunktswinkels $α$