Aufgaben zur Laplace-Wahrscheinlichkeit

1
Mila hat in ihrem Federmäppchen 10 bunte Stifte, für die sie eine Lieblingsanordnung hat.
Wie hoch ist die Wahrscheinlichkeit, dass die Stifte in Milas Lieblingsreihenfolge liegen, wenn ihr kleiner Bruder sie per Zufall hinlegt?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Wahrscheinlichkeiten
Ereignis $A$ : Milas Lieblingsreihenfolge
$P(A)={?}$
Da Milas Bruder die Stifte per Zufall hinlegt, sind alle Anordnungen gleich wahrscheinlich. Verwende daher die Formel für die Laplace-Wahrscheinlichkeiten.
In diese Formel setzt du
ein, denn es gibt ja nur eine Lieblingsanordnung.
Überlege dir nun, was $\left|\mathit\Omega\right|$ ist: Für den ersten Platz sind 10 Stifte möglich, für den zweiten nur noch 9, für den dritten 8 usw.
Gib 10! in deinen Taschenrechner ein.
Die Wahrscheinlichkeit, dass Milas Lieblingsreihenfolge per Zufall richtig hingelegt wird, liegt nur bei ungefähr 0,000 027 6 %!
2
Wie hoch ist die Wahrscheinlichkeit dafür, dass beim Skatspiel (32 Karten) zwei Damen im Skat (= zwei weggelegte Karten) liegen.
%

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Insgesamt: 32 Karten, davon 4 Damen
Es gibt 4 Dame-Karten, die beim ersten Aufdecken gezogen werden können. Beim zweiten gibt es eine Dame weniger. (Benutze hierfür die Multiplikation von Brüchen.)
$\frac4{32}\cdot\frac3{31}=\frac3{248}\approx1{,}2\,\%$
3
Zwei Laplace-Würfel werden nacheinander geworfen. Berechne die Wahrscheinlichkeit dafür, dass die Augensumme durch 3, 4 oder 5 teilbar ist.
%

Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Wahrscheinlichkeit
Berechne die Wahrscheinlichkeit durch die Formel des Laplace-Experiments.
Alle möglichen Augensummen sind 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Die durch 3, 4 oder 5 teilbaren Augensummen sind 3, 4, 5, 6, 8, 9, 10, 12.
Direkter Lösungsweg
Jetzt musst du nur noch alle Ergebnisse aufschreiben und bestimmen, wie viele davon die Augensumme 3, 4, 5, 6, 8, 9, 10, 12 haben. Da die Würfel nacheinander geworfen werden, kann kannst du zwischen einem ersten oder zweiten Wurf entscheiden und die Ergebnisse als $(\text{erster Wurf, zweiter Wurf})$ schreiben.
$\def\arraystretch{1.25} \begin{array}{rcl}\Omega&=& \{\left(1{,}1\right);\left(1{,}2\right);\left(1{,}3\right);\left(1{,}4\right);\left(1{,}5\right);\left(1{,}6\right); \\ & & \left(2{,}1\right);\left(2{,}2\right);\left(2{,}3\right);\left(2{,}4\right);\left(2{,}5\right);\left(2{,}6\right);\\ & &\left(3{,}1\right);\left(3{,}2\right);\left(3{,}3\right);\left(3{,}4\right);\left(3{,}5\right);\left(3{,}6\right); \\ & & \left(4{,}1\right);\left(4{,}2\right);\left(4{,}3\right);\left(4{,}4\right);\left(4{,}5\right);\left(4{,}6\right); \\ & & \left(5{,}1\right);\left(5{,}2\right);\left(5{,}3\right);\left(5{,}4\right);\left(5{,}5\right);\left(5{,}6\right); \\ & & \left(6{,}1\right);\left(6{,}2\right);\left(6{,}3\right);\left(6{,}4\right);\left(6{,}5\right);\left(6{,}6\right)\} \end{array}$
$|\Omega|=6\cdot6=36$
Mit E soll die Menge bezeichnet werden, deren Augensumme durch 3, 4 oder 5 teilbar sind.
$\def\arraystretch{1.25} \begin{array}{l c c} E & = & \{ \underbrace{(1{,}2);(2{,}1);(1{,}5);(5{,}1);(2{,}4);(4{,}2);(3{,}3);(3{,}6);(6{,}3);(4{,}5);(5{,}4);(6{,}6)}_{\text{durch 3 teilbar}}; \\ & & \underbrace{(1{,}3);(3{,}1);(2{,}2);(2{,}6);(6{,}2);(3{,}5);(5{,}3);(4{,}4)}_{\text{durch 4 (aber nicht durch 3) teilbar}}; \\ &&\underbrace{(1{,}4);(4{,}1);(2{,}3);(3{,}2);(4{,}6);(6{,}4);(5{,}5)}_{\text{durch 5 teilbar}} \}\end{array}$
$\Rightarrow\left|E\right|=27$
Nun kannst du die Mächtigkeit der Menge aller günstigen Ergebnisse $\left|E\right|$ durch die Mächtigkeit der Menge aller Ergebnisse $\left|\Omega\right|$ teilen.
$P\left(E\right)=\frac{27}{36}=0{,}75$
Rechne nun noch in Prozent um.
$\;\;\Rightarrow\;\;$ zu 75 % ist die Augensumme durch 3, 4 oder 5 teilbar.
Weiterer Lösungsweg über das Gegenereignis
Du kannst die Rechnung auch abkürzen indem du mit dem Gegenereignis rechnest. Dies bietet sich immer an, wenn die Anzahl der günstigen Ergebnisse groß ist und das Gegenereignis nur wenige Elemente enthält.
Das Ereignis $E = "\text{Augensumme ist durch 3, 4 oder 5 teilbar}"$ ist gleichbedeutend mit $"\text{Augensumme ist 3, 4, 5, 6, 8, 9, 10, 12}"$ .
Das Gegenereignis lautet $\overline{E}="\text{Augensumme ist nicht durch 3, 4 oder 5 teilbar}"$ oder eben $"\text{Augensumme ist 2{,}7 oder 11}"$ .
Da $P(E)=1-P(\overline{E})$ gilt, müssen wir nur noch $P(\overline{E})$ berechnen.
$\overline{E}=\{ \underbrace{(1{,}1)}_{\text{Augensumme 2}}; \underbrace{(1{,}6);(6{,}1);(2{,}5);(5{,}2);(3{,}4);(4{,}3)}_{\text{Augensumme 7}}; \underbrace{(5{,}6);(6{,}5)}_{\text{Augensumme 11}}\}$
$\Rightarrow|\overline{E}|=9$
Da wir oben schon berechnet haben, dass $|\Omega|=36$ ist, ist $P(\overline{E})=\frac{9}{36}$ und somit:
$\;\;\Rightarrow\;\;$ zu 75 % ist die Augensumme durch 3, 4 oder 5 teilbar.
4
In einer Familie gibt es 2 Söhne und 3 Töchter. Jeden Tag wird ausgelost, welches Kind den Tisch abräumen muss. Wie groß ist die Wahrscheinlichkeit dafür, dass
1. es die jüngste Tochter an zwei aufeinanderfolgenden Tagen trifft
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Berechne die Wahrscheinlichkeit, dass die jüngste Tochter ausgelost wird. Da alle Kinder gleich wahrscheinlich gezogen werden benutze Formel für Laplace-Experimente.
  $\displaystyle\frac{\text{Anzahl betroffener Kinder}}{\text{Gesamtanzahl Geschwister}}=\frac15$
  Berechne die Wahrscheinlichkeit , dass es die jüngste Tochter zweimal hintereinander trifft.
  $\frac15\cdot\frac15=\frac1{25}=0{,}04=4\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. es irgendein Kind an zwei aufeinanderfolgenden Tagen trifft
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier ist egal, welches der Kinder zweimal hintereinander gezogen wird. Deshalb ist es nicht wichtig, wer am ersten Tag gezogen wird. Berechne also die Wahrscheinlichkeit, dass am zweiten Tag ein bestimmtes Kind abräumen muss, nämlich das gleiche, das am ersten Tag ausgelost wurde.
  $\displaystyle\frac{\text{Anzahl betroffener Kinder}}{\text{Gesamtanzahl Geschwister}}=\frac15$
  Ergibt sich aus Formel für Laplace-Experimente.
  $\frac15=0{,}2=20\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. an zwei aufeinanderfolgenden Tagen Söhne abspülen müssen?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze dazu die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten.
  Bestimme dazu die Mächtigkeiten von $\Omega$ und $E$ = "an zwei Tagen nacheinander werden Söhne gezogen".
  Es gibt an jedem Tag eines von fünf Kindern ausgewählt wird, ergeben sich für zwei aufeinaderfolgende Tage $5\cdot 5=25$ Möglichkeiten.
  $\Rightarrow |\Omega|=25$
  Um an zweimal nacheinander Söhne zu ziehen gibt es $2\cdot2=4$ Möglichkeiten.
  $\Rightarrow |E|=4$
  Berechne damit die Wahrscheinlichkeit.
  $\displaystyle P(E)=\frac{|E|}{|\Omega|}=\frac{4}{25}=0{,}16=16\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
Eine natürliche Zahl x mit $20<x\le30$ wird willkürlich gezogen. Wie groß ist die Wahrscheinlichkeit, dass
1. eine Primzahl gezogen wird
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und A="x ist Primzahl".
  $A=\left\{23{,}29\right\}\;\;\Rightarrow\;\;\left|A\right|=2$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne nun die Wahrscheinlichkeit.
  $P\left(A\right)=\frac2{10}=0{,}2=20\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 20% ist die gezogene Zahl eine Primzahl.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. eine gerade Zahl gezogen wird
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und B="x ist gerade".
  $B=\left\{22{,}24{,}26{,}28{,}30\right\}\;\;\Rightarrow\;\;\left|B\right|=5$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne die Wahrscheinlichkeit.
  $P\left(B\right)=\frac5{10}=0{,}50=50\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 50% ist die gezogene Zahl eine gerade Zahl.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. eine durch 4 teilbare Zahl gezogen wird
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und C="x ist durch 4 teilbar".
  $C=\left\{24{,}28\right\}\;\;\Rightarrow\;\;\left|C\right|=2$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne die Wahrscheinlichkeit.
  $P\left(E\right)=\frac2{10}=0{,}2=20\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 20% ist die gezogene Zahl durch 4 teilbar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. eine durch 4 und gleichzeitig durch 6 teilbare Zahl gezogen wird?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und D="x ist durch 4 und durch 6 teilbar".
  $D=\left\{24\right\}\;\;\Rightarrow\;\;\left|D\right|=1$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne die Wahrscheinlichkeit.
  $P\left(D\right)=\frac1{10}=0{,}1=10\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 10% ist die gezogene Zahl durch 4 und 6 teilbar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6
Ein Prüfer gibt eine Liste von 8 Fragen aus. Bei der Prüfung wird er dem jeweiligen Prüfling 2 davon vorlegen, von denen dieser eine bearbeiten muss.
1. Felix Faul bereitet sich nur auf eine der 8 Fragen vor. Wie groß ist die Wahrscheinlichkeit, dass er seine Frage gestellt bekommt?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Dies ist ein zweistufiges Laplace-Experiment. In der ersten Stufe wird zufällig eine von acht, in der zweiten Stufe eine von sieben Fragen gezogen. Die von Felix vorbereitete Frage kommt entweder als erste, dann ist die zweite Frage egal, oder sie kommt als zweite, wenn als erstes eine andere gezogen wurde.
  $P_1$ : Wahrscheinlichkeit, dass die vorbereitete Frage gleich als erstes gezogen wird.
  $P_1=\frac{1}{8}\cdot\frac{7}{7}=\frac{1}{8}\cdot1=\frac{1}{8}$
  $P_2$ : Wahrscheinlichkeit, dass erst erst eine der anderen und dann die vorbereitete Frage gezogen wird.
  $P_2=\frac78 \cdot \frac 17=\frac18$
  $\Rightarrow P=P_1+P_2=\frac18+\frac18=\frac28=\frac14=25\%$
  Mit einer Wahrscheinlichkeit von $25\ \%$ wird Felix Faul die Frage gestellt, auf die er sich vorbereitet hat.
  Alternative Lösung
  Für diese Aufgabe benötigst du zusätzlich folgendes Grundwissen:
  Gegenereignis
  Du berechnest die Wahrscheinlichkeit, dass Felix die vorbereitete Frage nicht gestellt wird.
  $P_1$ : Wahrscheinlichkeit, dass die vorbereitete Frage nicht als erstes gezogen wird. Da es acht Fragen sind, ist
  $P_1=\frac{7}{8}$ .
  $P_2:$ Wahrscheinlichkeit, dass die vorbereitete Frage nicht als zweites gezogen wird. Nun sind es nur noch sieben Fragen, daher ist
  $P_2=\frac{6}{7}.$
  Die Gesamtwahrscheinlichkeit, dass die vorbereitete Frage nicht gezogen wird, ist also
  $P=P_1\cdot P_2=\frac{7}{8}\cdot \frac{6}{7}=\frac{6}{8}=\frac{3}{4}=75\%.$
  Da die Wahrscheinlichkeit, dass die von Felix vorbereitete Frage nicht gezogen wird, $75\%$ beträgt, ist die Wahrscheinlichkeit für das Ziehen $1-P=25\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Alexander Arglos bereitet sich auf 6 der 8 Fragen vor. Wie groß ist die Wahrscheinlichkeit dafür, dass er mindestens eine vorbereitete Frage vorgelegt bekommt?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Dies ist ein zweistufiges Laplace-Experiment. In der ersten Stufe wird eine von acht, in der zweiten Stufe eine von sieben Fragen gezogen.
  Hier ist es am einfachsten, über das Gegenereignis zu gehen. Die Wahrscheinlichkeit, dass mindestens eine der vorbereiten Fragen gezogen wird ist gleich 1 minus der Wahrscheinlichkeit, dass keine dieser Fragen gezogen wird.
  In der esten Stufe sind zwei von acht, in der zweiten Stufe eine von sieben Fragen nicht vorbereitet worden.
  $\text{P(keine der Fragen)}=\frac28\cdot \frac 17=\frac{2}{56}$
  $\Rightarrow \text{P(mindestens eine Frage)}$ $=1-\text{P(keine der Fragen)}$
  $=1-\frac{2}{56}=\frac{54}{56}\approx0{,}964=96{,}4\%$
  Zu etwa $96{,}4\ \%$ wird Alexander Arglos mindestens eine Frage gestellt, auf die er sich vorbereitet hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Es soll zufällig eine vierstellige Zahl aus den Ziffern 1, 2, 3 und 4 gebildet werden, bei der jede der Ziffern mehrmals vorkommen darf.
1. Beschreibe den Ablauf eines geeigneten Zufallsexperiments.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Als geeignetes Zufallsexperiment bietet sich das Drehen eines Glückrades mit 4 gleichgroßen Segmenten an. Dabei steht in jedem Segment eine Zahl zw. $1$ und $4$ und keine dieser Zahlen kommt doppelt vor.
  Wenn du das Glücksrad nun viermal drehst und dir jedes Mal die gedrehte Zahl aufschreibst, erhälst du eine vierstellige Zahl, die zufällig gebildet wurde, und jede Ziffer zw. $1$ und $4$ kann auch mehrmals vorkommen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie viele verschiedene Ergebnisse sind möglich?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
  Du kannst die Aufgabe mithilfe eines Baumdiagramms lösen. Du hast bei jeder Drehung jeweils 4 Möglichkeiten.Also gibt es
  $4^4=$ 256 Möglichkeiten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Ermittle die Wahrscheinlichkeiten folgender Ereignisse:
  A: Die Zahl enthält mindestens eine 2. B: Die gebildete Zahl endet auf 2.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Teilaufgabe 1
  Gesucht ist die Wahrscheinlichkeit, dass mindestens eine $2$ vorkommt.
  Verwende das Gegenereignis.
  $P("mind.eine \ 2")$ $=1-P("keine\;2")$
  Bestimme die Wahrscheinlichkeit des Gegenereignisses. Es gilt:
  Da keine $2$ vorkommen soll, gibt es nur noch $3$ Ziffern für die $4$ stellige Zahl. Wie in Teilaufgabe b) erhälst du z.B. mithilfe eines Baumdiagramms, dass $|A|=3^4$ ist.
  $|A|=|\{"keine 2"\}|=3^4$
  $|\Omega|=4^4$ (Teilaufgabe b) )
  $\Rightarrow P("keine\;2")=\left(\frac34\right)^4$
  $\Rightarrow P("mind.\;eine\;2")=1-\left(\frac34\right)^4=\frac{175}{256}\approx0{,}68=68\%$
  Teilaufgabe 2
  Gesucht ist die Wahrscheinlichkeit, dass die gebildete vierstellige Zahl am Ende eine 2 enthält.
  Es gilt:
  $P(A)=\frac{\left|A\right|}{\left|\Omega\right|}=\frac{|\{\text{"Zahl enthält eine 2 am Ende"}\}|}{|\Omega|}$
  Die Mächtigkeit von $\Omega$ wurde bereits in Teilaufgabe b) bestimmt. Bestimme die Mächtigkeit des Ereignisses $A$ , dass die vierstellige Zahl, eine $2$ am Ende enthält.
  Da der letzte Platz fix ist und die Ziffern mehrmals vorkommen können, können 4 Zahlen für 3 Plätze gewählt werden.
  $\Rightarrow |A|=4^3$
  Berechne nun $P(A)$ .
  $P(A)=\frac{\left|A\right|}{\left|\Omega\right|}=\frac{|\{\text{"Zahl enthält eine 2 am Ende"}\}|}{|\Omega|}=\frac{4^3}{4^4}=\frac14=0{,}25=25\%$
  Alternativ: Einfacher ist, zu erkennen, dass die $3$ vorderen Stellen für die Lösung irrelevant sind. Eine Ziffer von 4 an einer Stelle zu wählen, hat eben einfach eine Wahrscheinlichkeit von $25\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8
Aus sechs Ehepaaren werden zwei Personen ausgelost. Mit welcher Wahrscheinlichkeit handelt es sich um
1. zwei Damen?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Wahrscheinlichkeit
  Es handelt sich um ein zweistufiges Laplace-Experiment. In der ersten Stufe wird eine von zwölf Personen gezogen, in der zweiten Stufe eine von den verbleibenden elf.
  Hier muss in beiden Stufen eine Dame gezogen werden. Die Wahrscheinlichkeit hierfür ist die Anzahl der Damen durch die Gesamtzahl der Personen.
  $P=\frac{6}{12}\cdot\frac{5}{11}=\frac{30}{132}=\frac{5}{22}\approx 0{,}227=22{,}7\,\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. zwei Herren?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Wahrscheinlichkeit
  Es handelt sich um ein zweistufiges Laplace-Experiment. In der ersten Stufe wird eine von zwölf Personen gezogen, in der zweiten Stufe eine von den verbleibenden elf.
  Hier muss in beiden Stufen ein Herr gezogen werden. Die Wahrscheinlichkeit hierfür ist die Anzahl der Männer durch die Gesamtzahl der Personen.
  $P=\frac{6}{12}\cdot\frac{5}{11}=\frac{30}{132}=\frac{5}{22}\approx 0{,}227=22{,}7\,\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. eine Dame und einen Herren?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Wahrscheinlichkeit
  Es handelt sich um ein zweistufiges Laplace-Experiment. In der ersten Stufe wird eine von zwölf Personen gezogen, in der zweiten Stufe eine von den verbleibenden elf.
  Hier muss entweder in der ersten Stufe eine Dame und in der zweiten ein Herr gezogen werden oder umgekehrt. Die Wahrscheinlichkeit ist jeweils die Anzahl der Damen bzw. Herren durch die Gesamtzahl der Personen.
  $P(\text{erst Frau, dann Mann})=\frac{6}{12}\cdot\frac{6}{11}=\frac{36}{132}$
  Da die Wahrscheinlichkeit in beiden Fällen identisch ist, kann diese einfach verdoppelt werden.
  $P(\text{eine Dame und ein Herr})$
  $=P(\text{erst Frau, dann Mann})+P(\text{erst Mann, dann Frau})$
  $= \frac{36}{132}+\frac{36}{132}=\frac{36}{66}=\frac{6}{11}\approx0{,}545=54{,}5\,\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. ein Ehepaar?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Wahrscheinlichkeit
  Es handelt sich um ein zweistufiges Laplace-Experiment. In der ersten Stufe wird eine von zwölf Personen gezogen, in der zweiten Stufe eine von den verbleibenden elf.
  Hier muss in der zweiten Stufe der Ehepartner der in der ersten Stufe gezogenen Person gezogen werden. Die Wahrscheinlichkeit hierfür ist eins durch die Gesamtzahl der übrigen Personen. Welche Person dabei in der ersten Stufe gezogen wurde, ist egal.
  $P=\frac{12}{12}\cdot \frac{1}{11}=\frac{1}{11}\approx0{,}091=9{,}1\,\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
Gib für die folgenden Zufallsexperimente jeweils einen Ergebnisraum an und berechne die Wahrscheinlichkeiten der angegebenen Ereignisse.
1. Aus dem Wort „ZUFALLSEXPERIMENT“ wird zufällig ein Buchstabe ausgewählt.
  A: Es handelt sich um ein „E“. B: Es handelt sich um einen Konsonanten.
  C: Es handelt sich um einen Vokal.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier handelt es sich um ein Laplace-Experiment, da jeder Buchstabe mit gleicher Wahrscheinlichkeit gezogen werden kann.
  Benutze also die Formel für Laplace-Experimente, um die Wahrscheinlichkeit eines Ereignisses zu berechnen.
  Ereignis A
  A: Ein "E" wird gezogen.
  Bestimme die Mächtigkeit von A.
  |A| = Anzahl "E"s in "ZUFALLSEXPERIMENT" = 3
  Bestimme die Mächtigkeit von $\Omega$ .
  $|\Omega|=$ Anzahl der Buchstaben in "ZUFALLSEXPERIMENT" = 17
  Bestimme daraus P(A).
  $\displaystyle P(A)=\frac{|A|}{|\Omega|}=\frac{3}{17}\approx 17{,}6\%$
  Ereignis B
  B: Ein Konsonant wird gezogen.
  Bestimme die Mächtigkeit von B.
  |B|= Anzahl Konsonanten in "ZUFALLSEXPERIMENT" = 11
  Bestimme die Mächtigkeit von $\Omega$ .
  $|\Omega|=$ Anzahl der Buchstaben in "ZUFALLSEXPERIMENT" = 17
  Bestimme daraus P(B).
  $\displaystyle P(B)=\frac{|B|}{|\Omega|}=\frac{11}{17}\approx 64{,}7\%$
  Ereignis C
  C: Ein Vokal wird gezogen.
  Bestimme die Mächtigkeit von C.
  |C|= Anzahl Vokale in "ZUFALLSEXPERIMENT" = 6
  Bestimme die Mächtigkeit von $\Omega$ .
  $|\Omega|=$ Anzahl der Buchstaben in "ZUFALLSEXPERIMENT" = 17
  Bestimme daraus P(C).
  $\displaystyle P(C)=\frac{|C|}{|\Omega|}=\frac{6}{17}\approx 35{,}3\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Eine Lostrommel enthält 600 Lose. Zwei Drittel davon sind Nieten, 80 % des Restes ergeben Trostpreise, die übrigen Lose ergeben Hauptgewinne.
  A: Das gezogene Los ergibt einen Trostpreis.
  B: Das gezogene Los ergibt keinen Hauptgewinn.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Anzahl der Nieten, Trostpreise und Hauptgewinne
  Berechne zuerst die Anzahl der Nieten, Trostpreise und Hauptgewinne.
  Zweidrittel der Lose sind Nieten.
  Es gibt also $\frac{2}{3} \cdot 600 = 400$ Nieten
  Ein Drittel sind Gewinne und 80% davon sind Trostpreise.
  ( $\frac{1}{3} \cdot 600) \cdot 0{,}8 = 160$ Trostpreise
  $\Rightarrow$ 40 Hauptgewinne
  Wahrscheinlichkeiten berechnen
  Berechne nach der Laplace-Formel $P(A)$ und $P(B)$ .
  $P(A)=\frac{160}{600} \approx 26{,}7\%$
  $P(B)=\frac{600-40}{600}=\frac{560}{600}=93{,}3\%$
  $\;\;\Rightarrow$ Die Wahrscheinlichkeit einen Trostpreis zu ziehen liegt bei 26,7%, die Wahrscheinlichkeit keinen Hauptgewinn zu ziehen bei 93,3%.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10
Aus einem Bridge-Spiel (52 Karten) wird eine Karte gezogen. Berechne die Wahrscheinlichkeit folgender Ereignisse:
1. A: ="Die gezogene Karte ist eine Pikkarte"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13\;$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{im}\;\mathrm{Spiel}\;\mathrm{vorhandenen}\;\mathrm{Pikkarten}\;}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{13}{52}=\frac14=0{,}25=25\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. B: ="Die gezogene Karte ist eine Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{im}\;\mathrm{Spiel}\;\mathrm{vorhandenen}\;\text{Damen}\;}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{4}{52}=\frac{1}{13}\approx0{,}0769\approx7{,}7\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. C: ="Die gezogene Karte ist Pik-Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik-Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikdamen}=1$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{im}\;\mathrm{Spiel}\;\mathrm{vorhandenen}\;\mathrm{Pik}\text{damen}\;}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{1}{52}\approx0{,}0192=1{,}92\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. D: ="Die gezogene Karte ist eine Pikkarte oder eine Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik oder Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13$
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  Eine der vier Damen ist aber gleichzeitig Pik, darf also nicht doppelt gezählt werden.
  $\Rightarrow \text{Kartenzahl}=13+4-1=16$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}$
  $=\frac{16}{52}\approx0{,}3077\approx30{,}8\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. F: ="Die gezogene Karte ist eine Pikkarte, aber keine Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik aber keine Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13\;$
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikdamen}=1$
  Fasse das zur Anzahl der Karten zusammen.
  $\Rightarrow \text{Kartenzahl}=13-1=12$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{12}{52}=\frac3{13}=0{,}2308=23{,}1\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. G: ="Die gezogene Karte ist eine Dame, aber keine Pikkarte"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Dame aber nicht Pik", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikdamen}=1$
  Fasse das zur Kartenzahl zusammen.
  $\Rightarrow \text{Kartenzahl}=4-1=3$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac3{52}=0{,}058=5{,}8\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. H: ="Die gezogene Karte ist weder Pik noch Dame".
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist weder Pik noch Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13\;$
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Pikdamen}=1$
  Die Kartenzahl ist die Gesamtzahl abzüglich der Pik- und Damen-Karten. Dabei muss aber noch die Pikdame addiert werden, da diese doppelt abgezogen wird.
  $\Rightarrow \text{Kartenzahl}=52-13-4+1=36$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{36}{52}=\frac{9}{13}\approx0{,}692=69{,}2\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Eine Laplace-Münze wird 10mal geworfen. Berechne die Wahrscheinlichkeit dafür, dass beim k-ten Wurf zum ersten Mal Wappen geworfen wird für k=1,2,…10.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment

W=Wappen

Z=Zahl

Die Wahrscheinlichkeit dafür, dass beim ersten Wurf Wappen geworfen wird.

$P(W)=\frac12=50\%$

Die Wahrscheinlichkeit dafür, dass erst beim zweiten Wurf Wappen geworfen wird.

$P(ZW)=\frac12\cdot\frac12=\frac14=25\%$

Die Wahrscheinlichkeit dafür, dass erst beim dritten Wurf Wappen geworfen wird.

$P(ZZW)=\frac12\cdot\frac12\cdot\frac12=\frac18=12{,}5\%$

…

Die Wahrscheinlichkeit dafür, dass erst beim zehnten Wurf Wappen geworfen wird.

$P(ZZZZZZZZZW)=\left(\frac{1}{2}\right)^{10}=\frac{1}{1024}\approx0{,}098\%$

Allgemein:

Für den häufigen Wurf einer Laplace-Münze ergibt sich nach den Pfadregeln des Baumdiagramms der Stochastik die Wahrscheinlichkeit:

P("erst beim k-ten Wurf W") = $\left(\frac12\right)^k$

Tabelle mit allen Wahrscheinlichkeiten

$k$	$\text{Ereignis}$	$P(\text{Ereignis})$
$1$	$\{W\}$	$\frac 1 2=50\%$
$2$	$\{ZW\}$	$(\frac 1 2)^2=\frac 1 4=25\%$
$3$	$\{ZZW\}$	$(\frac 1 2)^3=\frac 1 8=12{,}5\%$
$4$	$\{ZZZW\}$	$(\frac 1 2)^4=\frac {1} {16}=6{,}25\%$
$5$	$\{ZZZZW\}$	$(\frac 1 2)^5=\frac {1} {32}=3{,}125\%$
$6$	$\{ZZZZZW\}$	$(\frac 1 2)^6=\frac {1} {64}=1{,}5625\%$
$7$	$\{ZZZZZZW\}$	$(\frac 1 2)^7=\frac {1} {128}\approx 0{,}781\%$
$8$	$\{ZZZZZZZW\}$	$(\frac 1 2)^8=\frac {1} {256}\approx 0{,}391\%$
$9$	$\{ZZZZZZZZW\}$	$(\frac 1 2)^9=\frac {1} {512}\approx 0{,}195\%$
$10$	$\{ZZZZZZZZZW\}$	$(\frac 1 2)^{10}=\frac {1} {1024}\approx 0{,}098\%$
allg.	$\{ZZZ\underbrace{W}_{k-te Stelle}\}$	$(\frac 1 2)^k$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

12
Zwei Buchstaben werden nacheinander aus dem Wort "LASSO" zufällig und ohne Zurücklegen ausgewählt. Die Buchstaben haben alle eine unterschiedliche Farbe.
Wie groß ist die Wahrscheinlichkeit dafür, dass ...
1. ... zwei Konsonanten gewählt werden?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  $S_1$ = pinkes S
  $S_2^{ }$ = grünes S
  $P\left(E\right)=\left\{LS_1;LS_2;S_1L;S_1S_2;S_2L;S_2S_1\right\}$
  $\;\;\,\Rightarrow\;\;\left|E\right|=6$
  $\def\arraystretch{1.25} \begin{array}{l}\Omega=\left\{LA;LS_1;LS_2;LO;AL;AS_1;AS_2;AO;S_1L;S_1A;S_1S_2;S_1O;S_2L;S_2A;S_2S_1;S_2O;OL;OA;OS_1;OS_2\right\}\\\;\;\Rightarrow\;\;\left|\Omega\right|=20\end{array}$
  Berechne die Wahrscheinlichkeit des Ereignises mit der Formel für Laplace-Experimente.
  $P\left(E\right)=\frac6{20}=0{,}3$
  Rechne nun noch in Prozent um.
  $\;\;\Rightarrow\;\;$ zu 30% zieht man 2 Konsonanten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. ... mindestens ein S darunter ist
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  $S_1$ = pinkes S
  $S_2^{ }$ = grünes S
  $P\left(E\right)=\left\{LS_1;LS_2;AS_1;AS_2;S_1L;S_1A;S_1S_2;S_1O;S_2L;S_2A;S_2S_1;S_2O;OS_1;OS_2\right\}\;\;$ \
  $\;\;\;\Rightarrow\;\;\left|E\right|=14$
  $\def\arraystretch{1.25} \begin{array}{l}\Omega=\left\{LA;LS_1;LS_2;LO;AL;AS_1;AS_2;AO;S_1L;S_1A;S_1S_2;S_1O;S_2L;S_2A;S_2S_1;S_2O;OL;OA;OS_1;OS_2\right\}\\\;\;\Rightarrow\;\;\left|\Omega\right|=20\end{array}$
  Berechne die Wahrscheinlichkeit des Ereignises mit der Formel für Laplace-Experimente.
  $P\left(E\right)=\frac{14}{20}=0{,}7$
  Rechne nun noch in Prozent um.
  $\;\;\Rightarrow\;\;$ zu 70% zieht man mindestens ein S.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. mindestens ein A darunter ist
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  $S_1$ = pinkes S
  $S_2^{ }$ = grünes S
  $P\left(E\right)=\left\{LA;AL;AS_1;AS_2;AO;S_1A;S_2A;OA\right\}\;\;$
  $\;\;\,\Rightarrow\;\;\left|E\right|=8$
  $\def\arraystretch{1.25} \begin{array}{l}\Omega=\left\{LA;LS_1;LS_2;LO;AL;AS_1;AS_2;AO;S_1L;S_1A;S_1S_2;S_1O;S_2L;S_2A;S_2S_1;S_2O;OL;OA;OS_1;OS_2\right\}\\\;\;\Rightarrow\;\;\left|\Omega\right|=20\end{array}$
  Berechne die Wahrscheinlichkeit des Ereignises mit der Formel für Laplace-Experimente.
  $P\left(E\right)=\frac8{20}=0{,}4$
  Rechne nun noch in Prozent um.
  $\;\;\Rightarrow\;\;$ zu 40% zieht man mindestens ein A.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
13
Wie groß ist die Wahrscheinlichkeit dafür, dass die Geburtstage von 12 Personen in 12 verschiedenen Monaten liegen? (mit gleicher Wahrscheinlichkeit für jeden Monat)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Für den ersten Monat kann jeder der 12 Leute Geburtstag haben, im 2. nur noch 11 Leute, da einer schon im 1. Monat hatte, im 3. noch 10 Leute usw.
$\frac{12}{12}\cdot\frac{11}{12}\cdot\frac{10}{12}\cdot\frac9{12}\cdot\frac8{12}\cdot\frac7{12}\cdot\frac6{12}\cdot\frac5{12}\cdot\frac4{12}\cdot\frac3{12}\cdot\frac2{12}\cdot\frac1{12}$
$=\frac{12!}{12^{12}}\approx0{,}005\,\%$
14
An einem Geburtstag setzen sich 5 Mädchen und 5 Jungen an einen runden Tisch. Berechne die Wahrscheinlichkeit für eine bunte Reihe.
Mit einer "bunten" Reihe ist gemeint, dass immer abwechselnd ein Junge und ein Mädchen sitzen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Informationen darüber, wie das hier geht, findest du im Artikel über Laplacewahrscheinlichkeiten; außerdem helfen dir Kenntnisse über Kombinatorik.
Es gibt 2 Möglichkeiten, die bunte Reihe aufzubauen.
Auf den 1. Platz kann sich jeder der 5 Jungen setzen, auf den 2. jedes der 5 Mädchen, auf den 3. nur noch 4 Jungen usw. (oder andersherum). Benutze hierfür die Multiplikation von Brüchen.
$2\cdot\frac5{10}\cdot\frac59\cdot\frac48\cdot\frac47\cdot\frac36\cdot\frac35\cdot\frac24\cdot\frac23\cdot\frac12\cdot1$ $\approx0{,}79\,\%$
15
In einem Spiel wird eine Münze dreimal geworfen. Erscheint zweimal nacheinander Zahl, so erhält der Spieler einen Preis. Mit welcher Wahrscheinlichkeit bekommt man einen solchen Preis?
%

Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Um einen Preis zu gewinnen, muss beim Münzwurf zweimal hintereinander Zahl fallen. Bestimme die Ergebnismenge $\Omega$ und such dir die Ergebnisse aus, die zweimal hintereinander Zahl enthalten. Die Laplace-Wahrscheinlichkeit berechnet sich dann aus $\frac{\text{Anzahl der günstigen Ergebnisse}}{\text{Anzahl aller Ergebnisse}}$ .
$K$ = Kopf
$Z$ = Zahl
$E$ = Ereignismenge "Es fällt zweimal Zahl hintereinander"
$\def\arraystretch{1.25} \begin{array}{l}\Omega=\left\{KKK;KKZ;KZZ;KZK;ZKK;ZKZ;ZZK;ZZZ\right\}\\\;\;\Rightarrow\;\;\left|\Omega\right|=8\end{array}$
$E=\left\{KZZ;ZZZ;ZZK\right\}\;\;$
$\;\;\,\Rightarrow\;\;\left|E\right|=3$
$P\left(E\right)=\frac38=0{,}375$
Rechne nun noch in Prozent um.
$\;\;\Rightarrow\;\;$ zu 37,5% gewinnt man den Preis.
16
In einer Schublade befinden sich 6 graue, 4 blaue und 4 rote Socken. Im Dunkeln werden der Schublade 2 Socken entnommen. Mit welcher Wahrscheinlichkeit sind beide Socken von der gleichen Farbe?
%

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Inhalt der Schublade: 14 Socken, davon 6 graue, 4 blaue und 4 rote.
Je nachdem, welche Socke zuerst gezogen wird, verändert sich die Wahrscheinlichkeit für die geforderte gleiche 2. Socke. Bei jeder der 3 Möglichkeiten können anfangs noch 14 Socken gezogen werden, beim 2. Ziehen nur noch 13, da eine schon herausgenommen wurde.
$\dfrac6{14}\cdot\dfrac5{13}+\dfrac4{14}\cdot\dfrac3{13}+\dfrac4{14}\cdot\dfrac3{13}$
Multipliziere die Brüche.
$\dfrac6{14}\cdot\dfrac5{13}+\dfrac4{14}\cdot\dfrac3{13}+\dfrac4{14}\cdot\dfrac3{13}\\$
$=\dfrac{15}{91}+\dfrac6{91}+\dfrac6{91}$
$=\dfrac{27}{91}\approx29{,}7\,\%$
17
Beschreibe ein Zufallsexperiment, das kein Laplace-Experiment ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Die folgende Lösung ist eine mögliche Lösung. Du hast weitere Ideen? Schreib sie uns doch in die Kommentare!
Ein Glücksrad hat 5 Sektoren (Felder).
Diese sind jedoch unterschiedlich groß. Deshalb ist es zum Beispiel wahrscheinlicher, eine 5 zu drehen als eine 1.
Es handelt sich also nicht um ein Laplace-Experiment.
Damit es sich um ein Zufallsexperiment handelt, muss es die folgenden Bedingungen erfüllen:
Es muss mehr als ein mögliches Ergebnis geben und alle möglichen Ergebnisse müssen bekannt sein (sonst kein Zufallsexperiment)
Es darf nicht klar sein, welches Ergebnis eintreten wird (sonst kein Zufallsexperiment)
Wenn es jetzt zugleich kein Laplace-Experiment sein soll, dürfen die einzelnen Ergebnisse nicht alle gleich wahrscheinlich sein.
18
Eine Urne enthält 7 blaue und 5 rote Kugeln. Man zieht 4 Kugeln einmal mit und einmal ohne Zurücklegen. Dabei erhält man die Farbfolge blau, rot, rot, blau. Wie hoch ist die Wahrscheinlichkeit für dieses Ergebnis in beiden Fällen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
b=blau
r=rot
Ziehen mit Zurücklegen
Die Wahrscheinlichkeit bleibt immer $\frac7{12}$ für eine blaue Kugel bzw. $\frac5{12}$ für eine rote Kugel, da alle Kugeln wieder zurückgelegt werden.
$P$ („bei 4-maligem Ziehen brrb-Farbreihenfolge“)
$=\frac{5}{12}\cdot\frac{7}{12}\cdot\frac{7}{12}\cdot\frac{5}{12}$
$=\frac{1225}{20736}\approx5{,}91\,\%$
Ziehen ohne Zurücklegen
Sobald eine Kugel herausgenommen wird, ist beim nächsten Ziehen eine Kugel weniger in der Urne.
Daher ist die Wahrscheinlichkeit für eine blaue Kugel beim ersten Zug $\frac{7}{12}$ .

Danach sind noch 11 Kugeln in der Urne. 5 davon sind rot. Also ist die Wahrscheinlichkeit $\frac{5}{11}$ als zweites eine rote Kugel zu ziehen.
Danach sind noch 10 Kugeln in der Urne. 4 davon sind rot. Also ist die Wahrscheinlichkeit $\frac{4}{10}$ als drittes eine rote Kugel zu ziehen.
Danach sind noch 9 Kugeln in der Urne. 6 davon sind rot. Also ist die Wahrscheinlichkeit $\frac{6}{9}$ als viertes eine blaue Kugel zu ziehen.
$P$ („bei 4-maligem Ziehen brrb-Farbreihenfolge“)
$=\frac{7}{12}\cdot\frac{5}{11}\cdot\frac{4}{10}\cdot\frac{6}{9}$
$=\frac7{99}\approx7{,}07\,\%$
19
Bei einem Gewinnspiel auf dem Volksfest stehen zwei Möglichkeiten für Max zur Verfügung. Bei der ersten gewinnt man, wenn man aus einer Urne mit 6 weißen und 4 roten Kugeln bei einmaligem Ziehen eine weiße Kugel erhält, bei der zweiten, indem man aus zwei Urnen, einer mit gleich vielen weißen und roten Kugeln und einer wie bei der ersten Möglichkeit, zwei verschiedenfarbige Kugeln zieht. Welche der beiden Möglichkeiten sollte Max wählen, um eine möglichst hohe Wahrscheinlichkeit für einen Gewinn zu haben?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
1. Möglichkeit:
Insgesamt: 6w ; 4r
Es gibt 6 Möglichkeiten, dass eine weiße Kugel gezogen wird.
$P({\text{"bei einmaligem Ziehen 1 weiße Kugel"}})=\frac6{10}=60\%$
2. Möglichkeit:
Urne 1: 6w ; 4r
Urne 2: x w ; x r
Wenn Max in Urne 1 zuerst eine Weiße zieht, muss er in Urne 2 eine Rote ziehen.
Wenn er in Urne 1 zuerst eine Rote zieht, muss er in Urne 2 eine Weiße ziehen.
In Urne 2 ist die Anzahl der verschiedenfarbigen Kugeln gleich ( $\rightarrow\;x\;r\;;\;x\;w$ ), deshalb ist jeweils die Chance die andere Farbe wie in Urne 1 zu ziehen $\frac12$ .
$\frac6{10}\cdot\frac12+\frac4{10}\cdot\frac12=\frac6{20}+\frac4{20}$
$=\frac{10}{20}=\frac12=50\%$
Multipliziere die Brüche im ersten Schritt und addiere die Brüche danach.
$\;\Rightarrow$ Es ist günstiger für Max die 1. Möglichkeit zu nehmen, da er eine höhere Gewinnchance hat.
20
Gib für folgende Zufallsexperimente jeweils einen Ergebnisraum an und entscheide, ob es sich um ein Laplace-Experiment handelt:
1. Ein aus dem abgebildeten Netz gebastelter „Würfel“ wird geworfen und die oben liegende Farbe wird notiert.
  Das ist ein Laplace-Experiment.
  Das ist kein Laplace-Experiment.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Es gibt drei Elementarereignisse, Grün, Gelb und Orange. Deren Wahrscheinlichkeit ist jeweils die Anzahl der entsprechend gefärbten Würfelseiten durch die Gesamtzahl der Würfelseiten.
  $\mathrm{Grün}\colon\;\,\dfrac28=\dfrac14=25\,\%\\\mathrm{Gelb}\colon\dfrac38=37{,}5\,\%\\\mathrm{Orange}\colon\;\dfrac38=37{,}5\,\%$
  $\Rightarrow$ Kein Laplace-Experiment, da die Elementarereignisse unterschiedlich wahrscheinlich sind.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
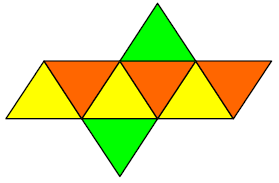
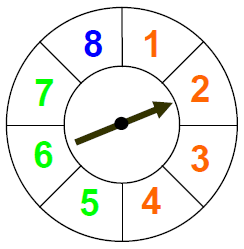
2. Das abgebildete Glücksrad wird gedreht und die angezeigte Zahl wird betrachtet.
  Das abgebildete Glücksrad wird gedreht und die angezeigte Farbe wird betrachtet.
  1 ist ein Laplace-Experiment.
  1 ist kein Laplace-Experiment.
  2 ist ein Laplace-Experiment.
  2 ist kein Laplace-Experiment.
  
  Laplace-Experiment
  Teilaufgabe 1
  Es gibt acht Elementarereignisse, die Zahlen von 1 bis 8. Die Wahrscheinlichkeit für das Eintreten eines Ereignisses ist gleich die Anzahl der entsprechenden Felder geteilt durch die Gesamtzahl der Felder.
  Da hier jede Zahl einem Feld entspricht, haben sie alle die Wahrscheinlichkeit $\frac{1}{8}$ .
  Insbesondere sind alle gleichwahrscheinlich, es handelt sich also um ein Laplace-Experiment.
  Teilaufgabe 2
  Hier gibt es drei Elementarereignisse, Orange, Grün und Blau. Diese haben jeweils die Wahrscheinlichkeit gleich der Anzahl der entsprechend farbigen Felder geteilt durch die Gesamtzahl der Felder:
  Orange: $\dfrac48=\dfrac12=50\,\%$
  Grün: $\dfrac38=37{,}5\,\%$
  Blau: $\dfrac18=12{,}5\,\%$
  $\Rightarrow$ Kein Laplace-Experiment, da die Elementarereignisse nicht gleichwahrscheinlich sind.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Aus einer Tüte mit 13 roten, 9 grünen, 12 gelben und 21 weißen Gummibärchen wird zufällig ein Gummibärchen ausgewählt.
  Das ist ein Laplace-Experiment.
  Das ist kein Laplace-Experiment
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Es gibt vier Elementarereignisse, Rot, Grün, Gelb und Weiß. Diese haben alle die Wahrscheinlichkeit gleich der Anzahl der jeweiligen Gummibärchen geteilt durch die Gesamtzahl der Gummibärchen. Berechne also erst die Gesamtzahl und dann die Wahrscheinlichkeiten:
  $13+9+12+21=55$
  Gesamtmenge ist Summe der verschiedenen Gummibärchen
  Rot: $\dfrac{13}{55}=23{,}6\,\%$
  Grün: $\dfrac9{55}=16{,}4\,\%$
  Gelb: $\dfrac{12}{55}=21{,}8\,\%$
  Weiß: $\dfrac{21}{55}=38{,}2\,\%$
  $\Rightarrow$ Es handelt sich nicht um ein Laplace-Experiment, da die Wahrscheinlichkeiten ungleich sind.
  Bemerkung: Die Rechnung ist nicht unbedingt nötig, schon aus der unterschiedlichen Anzahl der Gummibärchen ergibt sich, dass die Wahrscheinlichkeiten nicht gleich sein können.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
21
Die Oberfläche eines Würfels wird blau eingefärbt.
Dann wird der Würfel durch 6 parallel zur Würfeloberfläche verlaufende Schnitte in 27 kongruente Teilwürfel zerlegt.
Wie groß ist die Wahrscheinlichkeit dafür, dass ein willkürlich herausgegriffener Teilwürfel
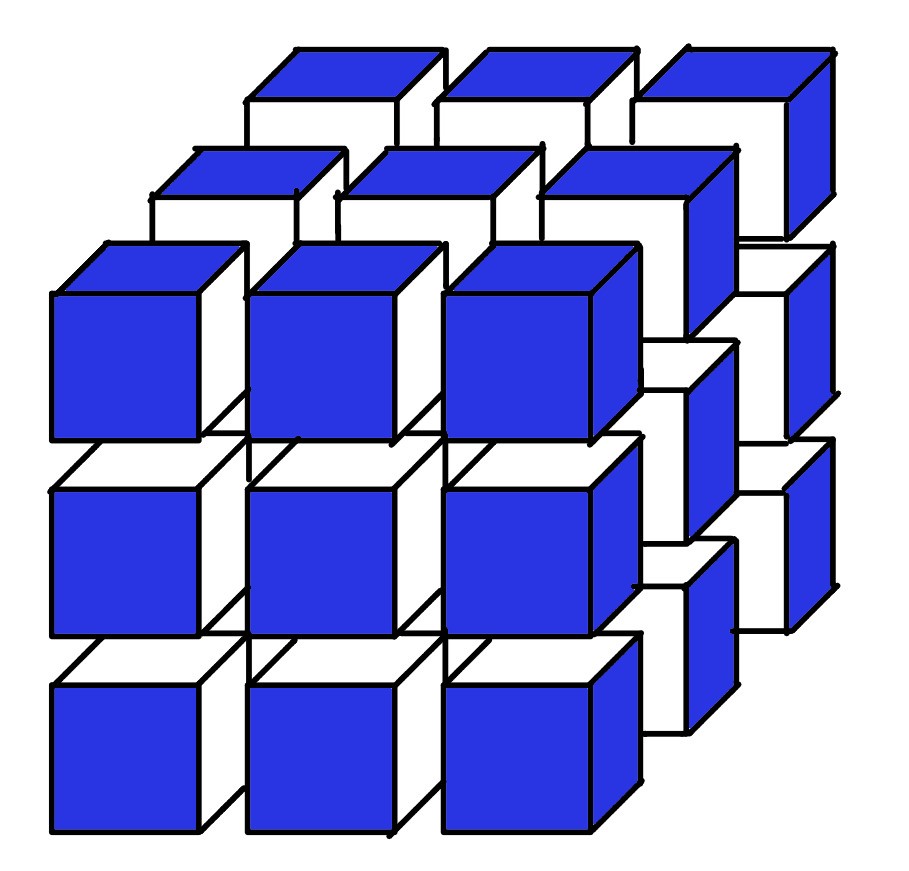
1. keine blaue Fläche hat. Gib die Antwort als Dezmalzahl ein.
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  $\left|\mathrm{E}\right|=1$
  $\left|\mathrm{\Omega}\right|=27$
  $\mathrm P\left(\mathrm E\right)=\frac1{27}=3{,}7\%$
  $\Rightarrow$ Zu 3,7% zieht man einen Teil, dass keine blauen Flächen hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. genau zwei blaue Flächen hat? Gib die Antwort als Dezimalzahl ein
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  $\left|\mathrm E\right|=12$
  $\left|\mathrm\Omega\right|=27$
  $\mathrm P\left(\mathrm E\right)=\frac{12}{27}=44{,}4\%$
  $\Rightarrow$ Man zieht zu 44,4% ein Würfelteil, das zwei eingefärbte Seiten hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Drei L-Würfel werden gleichzeitig geworfen. Berechne die Wahrscheinlichkeiten folgender Ereignisse:

"Keine Sechs"

"Genau eine Sechs"

"Genau zweimal Sechs"

"Alle drei Würfel zeigen Sechs"
%

Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation
$\displaystyle P\, (\text{"1 Sechs"})$ $=$ $\displaystyle \frac1{6}$
$\displaystyle \frac1{6}\cdot\frac1{6}\cdot\frac1{6}=\left(\frac1{6}\right)^3$ $=$ $\displaystyle \frac1{216}\approx0{,}46\,\%$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Wahrscheinlichkeit der drei Würfel miteinander multiplizieren.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle P(\text{einmal keine }6)$	$=$	$\displaystyle \frac{5}{6}$
$\displaystyle P(\text{dreimal keine }6)$	$=$	$\displaystyle \frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}$
	$=$	$\displaystyle \left(\frac{5}{6}\right)^3$
	$≈$	$\displaystyle 57{,}9\%$

$\displaystyle P\,(\text{"eine Sechs"})$	$=$	$\displaystyle \frac1{6}$
$\displaystyle P\, (\text{"keine Sechs"})$	$=$	$\displaystyle \frac5{6}$

$\displaystyle P\, (\text{"eine Sechs"})$	$=$	$\displaystyle \frac1{6}$
$\displaystyle P\, (\text{"keine Sechs"})$	$=$	$\displaystyle \frac5{6}$

Aufgaben zur Laplace-Wahrscheinlichkeit

Direkter Lösungsweg

Weiterer Lösungsweg über das Gegenereignis

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Teilaufgabe 1

Teilaufgabe 2

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ereignis A

Ereignis B

Ereignis C

Hast du eine Frage oder Feedback?

Anzahl der Nieten, Trostpreise und Hauptgewinne

Wahrscheinlichkeiten berechnen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Tabelle mit allen Wahrscheinlichkeiten

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ziehen mit Zurücklegen

Ziehen ohne Zurücklegen

1. Möglichkeit:

2. Möglichkeit:

Hast du eine Frage oder Feedback?

Laplace-Experiment

Teilaufgabe 1

Teilaufgabe 2

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?