Aufgaben zur Kurvendiskussion mit Exponentialfunktion und Logarithmus

Es ist folgende Funktion gegeben:

\displaystyle \mathrm f\left(\mathrm x\right)=\frac{\left(2\mathrm x^2-2\right)\cdot\ln\left(\left(\mathrm x-1\right)^2\right)}{1+\mathrm x}

In den Teilaufgaben findest du alles, was du für diese Funktion berechnen könntest.

Suche dir das heraus, was du üben möchtest.

Bei späteren Teilaufgaben kann auf frühere Ergebnisse zurückgegriffen werden.

Ist dir nicht sofort klar, woher diese Ergebnisse kommen, dann bearbeite zunächst diese früheren Teilaufgaben zur Wissensauffrischung.

Bestimme den Definitionsbereich und die Art der Definitionslücken.

Definitionsbereich

Der Definitionsbereich ist der Zahlenbereich, der für die Funktion zulässig ist. Um ihn zu bestimmen gehst du von den reellen Zahlen $\mathbb{R}$ aus und überprüfst, welche Zahlen nicht in die Funktion eingesetzt werden dürfen.

Die Funktion ist eine Kombination aus einem Bruch, Polynomen und einer Logarithmusfunktion. Bei Polynomen darf man für $x$ ganz $\mathbb R$ einsetzen. Bei Brüchen darf der Nenner nicht 0 sein. Logarithmen darf man nur von positiven Zahlen nehmen.

Der Nenner darf nicht Null werden.

Setze den Nenner $1+x$ gleich $0$ , um herauszufinden, welche Zahl nicht für $x$ eingesetzt werden darf.

$\displaystyle 1+x$	$=$	$\displaystyle 0$	$\displaystyle -1$
$\displaystyle x$	$=$	$\displaystyle -1$

$x=-1$ ist eine Definitionslücke.

Das Argument des Logarithmus muss größer als 0 sein.

Setze $(x-1)^2>0$ .

Da Quadratische Funktionen nicht negativ sind, musst du nur ausschließen, dass der Term 0 wird.

$\displaystyle \left(x-1\right)^2$	$=$	$\displaystyle 0$	$\displaystyle \sqrt{ }$
	↓	Ziehe die Wurzel.
$\displaystyle x-1$	$=$	$\displaystyle 0$	$\displaystyle +1$
$\displaystyle x$	$=$	$\displaystyle 1$

$x=1$ ist eine Definitionslücke.

Definitionsmenge

$\mathrm D_\mathrm f=\mathbb{R}\setminus\left\{-1;\;1\right\}$

Art der Definitionslücken

Es gibt zwei Arten von Definitionslücken: hebbare und nicht hebbare.

Hebbare Definitionslücken liegen dann vor, wenn die Funktion an jenen Stellen stetig fortsetzbar sind. Das ist zum Beispiel bei Brüchen der Fall, wenn die Nennernullstelle zugleich eine Zählernullstelle ist.

Definitionslücke $x=-1$

Um das zu überprüfen, setzt du die oben bestimmte Nennernullstelle in den Zähler ein:

$\left(2\left(-1\right)^2-2\right)\cdot\ln\left(\left(\left(-1\right)-1\right)^2\right)=0\cdot\ln\left(4\right)=0$

Die Nennernullstelle $-1$ ist also eine Zählernullstelle und damit eine hebbare Definitionlücke.

Definitionslücke $x=1$

Als nächstes willst du die Art der Definitionslücke von $1$ herausfinden. Dabei kannst du nicht analog zu oben argumentieren, da in diesem Fall die Lücke durch die Logarithmusfunktion verursacht wird.

Du musst zeigen, dass die Funktion an der Stelle $1$ entweder stetig fortsetzbar ist oder nicht.

Falls die Funktion von rechts und von links an die $1$ angenähert den selben endlichen Wert annehmen, dann ist die Funktion stetig fortsetzbar und damit eine hebbare Definitionslücke.

Du überprüfst:

\displaystyle \mathrm f\left(\mathrm x\right)=\frac{\left(2\mathrm x^2-2\right)\cdot\ln\left(\left(\mathrm x-1\right)^2\right)}{1+\mathrm x}

Alternativ kannst du auch mit den Regeln von Regeln von L'Hospital argumentieren.

Analog gilt:

\displaystyle \mathrm f\left(\mathrm x\right)=\frac{\left(2\mathrm x^2-2\right)\cdot\ln\left(\left(\mathrm x-1\right)^2\right)}{1+\mathrm x}

Es folgt insgesamt, dass $1$ ebenfalls eine hebbare Definitionslücke ist.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Vereinfache die Funktionsgleichung.

Berechne die Grenzwerte an den Rändern des Definitionsbereichs.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte

Zu den Rändern des Definitionsbereichs zählen Grenzen im Unendlichen, Intervallgrenzen und die Definitionslücken, also jeder Punkt, der nicht in einem Intervall des Definitionsbereichs liegt.

Der Definitionsbereich lautet $D_f=\mathbb{R}\setminus\left\{-1;1\right\}$

Die Ränder sind also $-\infty;-1;1;\infty$

Rechne am besten hier schon mit dem vereinfachten Funktionsterm aus der 2. Teilaufgabe.

Grenzwert im Unendlichen

$\def\arraystretch{1.25} \begin{array}{l}\lim_{x\rightarrow -\infty} f\left( x\right)&=\lim_{ x\rightarrow-\infty}2 \underbrace{\left( x-1\right)}_{\rightarrow -\infty} \underbrace{\ln\left(\left(x-1\right)^2\right)}_{\rightarrow\infty}=-\infty\end{array}$

Ein Faktor geht gegen $-\infty$ , einer gegen $+\infty$ . Da minus mal plus minus ergibt und $\infty \cdot \infty=\infty$ , ist der Grenzwert $-\infty$ .

$\lim_{ x\rightarrow\infty} f\left( x\right)=\lim_{ x\rightarrow\infty}2\underbrace{\left( x-1\right)}_{\rightarrow\infty}\underbrace{\ln\left(\left(x-1\right)^2\right)}_{\rightarrow\infty}=\infty$

Grenzwert an den Definitionslücken von beiden Seiten

Grenzwerte an $x=-1$

$\def\arraystretch{1.25} \displaystyle\begin{array}{rcl}\lim_{ x\rightarrow-1^-} f\left( x\right)&=&\lim_{ x\rightarrow-1^-}2\left( x-1\right)\ln\left(\left( x-1\right)^2\right)\\&=&2\cdot\left(-2\right)\cdot\ln\left(4\right)\\&=&-4\cdot\ln\left(4\right)\end{array}$

$\def\arraystretch{1.25} \displaystyle\begin{array}{rcl}\lim_{ x\rightarrow-1^+} f\left( x\right)&=&\lim_{ x\rightarrow-1^+}2\left( x-1\right)\ln\left(\left( x-1\right)^2\right)\\&=&2\cdot\left(-2\right)\cdot\ln\left(4\right)\\&=&-4\cdot\ln\left(4\right)\end{array}$

Grenzwerte an $x=1$

Hier erhältst du Produkt aus 0 und $\infty$ . Da du nicht weißt, wie das Ergebnis lautet, wendest du die Regel von L'Hospital an mit dem Logarithmus im Zähler und $\frac{1}{2(x - 1)}$ im Nenner.

$\displaystyle \lim_{\mathrm{x}\rightarrow1^-}f(x)$	$=$	$\displaystyle \lim_{\mathrm x\rightarrow1^-}\;2\underbrace{\left(\mathrm x-1\right)}_{=0}\underbrace{\ln\left(\left(x-1\right)^2\right)}_{\rightarrow-\infty}$
	$=$	$\displaystyle \lim_{ x\rightarrow1^-}\frac{\overbrace{\ln\left(\left(x-1\right)^2\right)}^{\rightarrow-\infty}}{\underbrace{\frac{1}{2\left( x-1\right)}}_{\rightarrow-\infty}}$
	↓	Du leitest jetzt Zähler und Nenner separat ab.
	$=$	$\displaystyle \lim_{ x\rightarrow1^-}\frac{\frac{2\left( x-1\right)}{\left(\mathrm x-1\right)^2}}{-\frac1{2\left(x-1\right)^2}}$
	$=$	$\displaystyle \lim_{ x\rightarrow1^-}\frac{-2\left( x-1\right)^2\cdot2\left(x-1\right)}{\left( x-1\right)^2}$
	$=$	$\displaystyle \lim_{ x\rightarrow1^-}-4\left(x-1\right)$
	$=$	$\displaystyle 0$

$\displaystyle \underset{ \text{L'Hospital}}\Rightarrow \lim_{x\rightarrow1^-}f\left(x\right)=0=\lim_{ x\rightarrow1^+} f\left( x\right)$

Die Regel von L'Hospital liefert auch hier mit 0 einen konkreten Wert.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Setze die Funktion $f$ - wenn möglich - stetig zu einer Funktion $\hat f$ fort.

Will man eine Funktion stetig fortsetzen, dann muss man die Funktion an allen Unstetigkeitsstellen - und nur dort - neu definieren.
Deswegen erhält man dann eine abschnittsweise definierte Funktion.
Hier hast du:
Diese Funktion hat Definitionslücken bei -1 und 1 und damit dort auch Unstetigkeitsstellen.
Beide sind keine Polstellen, sondern behebbare Definitionslücken, also ist die Funktion stetig fortsetzbar.
Für die kritischen Punkte gilt
$\def\arraystretch{1.25} \begin{array}{ll}\underset{ x\rightarrow-1}\lim f\left( x\right)&=-4\ln\left(4\right)\\\lim_{ x\rightarrow1} f\left( x\right)&=0\end{array}$
Nun definierst du die Funktion neu und setzt an den kritischen Stellen jeweils den Grenzwert ein:
$\def\arraystretch{1.25} \widehat{f}\left( x\right)=\left\{\begin{array}{lcl}-4\cdot\ln\left(4\right)&\text{für}& x=-1\\0&\text{für}& x=1\\f\left( x\right)&\text{sonst}&\end{array}\right.$
Die Funktion $\widehat{f}$ ist jetzt die stetig fortgesetzte Version von $f$ ohne Lücken.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Asymptoten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Asymptote
Es gibt waagerechte, senkrechte und schiefe Asymptoten .
Waagerechte Asymptoten treten auf, wenn ein Grenzwert im Unendlichen einen konkreten Zahlenwert liefert.
Senkrechte Asymptoten treten auf, wenn der Grenzwert an Definitionslücken keinen konkreten Zahlenwert, sondern $\pm\infty$ liefert.
Schiefe Asymptoten treten manchmal bei Bruchtermen auf.
Waagerechte Asymptoten
Die Grenzwerte im Unendlichen sind $\infty$ . Deshalb gibt es keine waagerechten Asymptoten.
Senkrechte Asymptoten
Die Grenzwerte an den Definitionslücken sind $-4 \ln(4)$ und $0$ . Deshalb gibt es keine senkrechten Asymptoten.
Schiefe Asymptoten
Schiefe Asymptoten können nur bei gebrochen-rationalen Funktionen vorkommen (also ohne den Logarithmus). Deshalb gibt es keine schiefen Asymptoten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Nullstellen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Nullstellen sind diejenigen Punkte, an denen der y-Wert den Wert 0 annimmt.
Zur Berechnung musst du die Funktion nur gleich 0 setzen.
$\displaystyle f(x)$ $=$ $\displaystyle 0$
$\displaystyle 2\left( x-1\right)\ln\left(\left( x-1\right)^2\right)$ $=$ $\displaystyle 0$
Ein Produkt ist $0$ , wenn einer der Faktoren $0$ ist. Setze also die Faktoren des Terms gleich $0$ .
$x-1=0$ gilt, wenn $x=1$ ist.
$\ln((x-1)^2)=0$ , wenn $(x-1)^2=1$ ist $\Rightarrow x=0$ oder $x=2$
Da aber $1\notin{\mathbb D}_ f$ , hat die Funktion nur zwei Nullstellen:
${\mathrm{Nst}}_1\left(0\vert0\right)$ und ${\mathrm{Nst}}_2\left(2\vert0\right)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme die Extrempunkte.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrempunkte

Extremstellen sind die Stellen des Funktionsgraphen, bei denen der Graph nicht steigt oder fällt. Die Steigung des Funktionsgraphen berechnet man über die Ableitung der Funktion. Soll die Steigung 0 sein, so musst du die Ableitung gleich 0 setzen. Damit erhältst du die Lage der Extremstellen.

Extremstelle berechnen

$f\left( x\right)=2\left( x-1\right)\cdot\ln\left(\left( x-1\right)^2\right)$

Für die Ableitung dieser Funktion brauchst du die Produktregel und die Kettenregel.

Bei der Kettenregel leitest du die Funktionen von außen nach innen ab, also zuerst den Logarithmus, dann die quadrierte Klammer und zum Schluss das $x$ , das als Ableitung 1 liefert.

$\displaystyle f'\left(x\right)$	$=$	$\displaystyle 2\cdot\ln\left(\left(x-1\right)^2\right)+2\cdot\left(x-1\right)\cdot\frac{2\cdot\left(x-1\right)}{\left(x-1\right)^2}$
	↓	Kürze den zweiten Summanden mit $(x-1)^2$ .
	$=$	$\displaystyle 2\cdot\ln\left(\left(x-1\right)^2\right)+4$
	$=$	$\displaystyle 2\cdot\left(\ln\left(\left(x-1\right)^2\right)+2\right)$

Jetzt musst du diesen Ausdruck gleich 0 setzen.

$\displaystyle f'\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle 2\cdot\left(\ln\left(\left(x-1\right)^2\right)+2\right)$	$=$	$\displaystyle 0$	$\displaystyle :2$
$\displaystyle \ln\left(\left(x-1\right)^2\right)+2$	$=$	$\displaystyle 0$	$\displaystyle -2$
$\displaystyle \ln\left(\left(x-1\right)^2\right)$	$=$	$\displaystyle -2$
	↓	Löse den Logarithmus mithilfe der e-Funktion auf.
$\displaystyle e^{\ln\left(\left(x-1\right)^2\right)}$	$=$	$\displaystyle e^{-2}$
$\displaystyle \left(x-1\right)^2$	$=$	$\displaystyle \frac{1}{e^2}$
$\displaystyle \left(x-1\right)^2$	$=$	$\displaystyle \left(\frac{1}{e}\right)^2$	$\displaystyle \sqrt{ }$
	↓	Ziehe die Wurzel.
$\displaystyle x-1$	$=$	$\displaystyle \pm\frac{1}{e}$	$\displaystyle +1$
$\displaystyle x$	$=$	$\displaystyle 1\pm\frac{1}{e}$

Jetzt hast du die Lage ( $x$ - Werte) der Extrempunkte bestimmt. Beide liegen im Definitionsbereich. Für die $y$ - Werte musst du nun die erhaltenen $x$ - Werte in die Funktion $f(x)$ einsetzen.

Koordinaten der Extrempunkte

$\def\arraystretch{1.25} \displaystyle\begin{array}{rcl} f\left(1-\frac1{ e}\right)&=&2\left(1-{\frac1{ e}}-1\right)\cdot\ln\left(\left(1-{\frac1{ e}}-1\right)^2\right)\\&=&-\frac2{ e}\cdot\ln\left(\frac1{ e^2}\right)=-\frac2{ e}\cdot\left(-2\right)\ln\left( e\right)\\&=&\frac4{ e}\end{array}$

$\displaystyle\Rightarrow{\mathrm{EP}}_1\left(1-{\frac1{ e}}\left|\frac4{ e}\right)\right.$

$\def\arraystretch{1.25} \begin{array}{rcl} f\left(1+\frac1{ e}\right)&=&2\left(1+{\frac1{ e}}-1\right)\cdot\ln\left(\left(1+{\frac{1}{e}}-1\right)^2\right)\\&=&\frac2{ e}\cdot\ln\left(\frac{1}{ e^2}\right)=\frac2{ e}\cdot\left(-2\right)\ln\left( e\right)\\&=&-\frac{4}{e}\end{array}$

$\displaystyle\Rightarrow{\mathrm{EP}}_2\left(1+{\frac1{ e}}\left|-\frac4{ e}\right)\right.$

Art der Extrempunkte bestimmen

Nachdem du die Koordinaten bestimmt hast, fehlt nur noch die Art der Extrempunkte.

Diese lässt sich entweder durch das Überprüfen des Monotonieverhaltens im Definitionsbereich oder durch einsetzen der $x$ - Werte der Extrema in die 2. Ableitung bestimmen.

Für ein Minimum $x_{\min}$ gilt: $f'\left(x_{\min}^-\right)<0\wedge f'\left(x_{\min}^+\right)>0$ bzw. meistens $f''\left(x_{\min}\right)>0$ .
Für ein Maximum $x_{\max}$ gilt: $f'\left(x_{\max}^-\right)>0\wedge f'\left(x_{\max}^+\right)<0$ bzw. meistens $f''\left(x_{\max}\right)<0$ .
Für einen Terrassenpunkt gilt: $f'\left({x_\mathrm{TP}}^-\right)\lt0\wedge f'\left({x_\mathrm{TP}}^+\right)\gt0 \vee f'\left({x_\mathrm{TP}}^-\right)\gt 0 \wedge f'\left({x_\mathrm{TP}}^+\right)\lt0$ bzw. meistens $f''\left(x_\mathrm{TP}\right) = 0 \wedge f'''\left(x_\mathrm{TP}\right) \neq 0$ .

Für eine Erklärung der Zeichen sieh dir den Artikel Logikverknüpfungen an.

Um unabhängig von einer möglicherweise komplizierten 2. Ableitung zu bleiben, überprüfst du hier am Besten das Monotonieverhalten.

Art der Extrempunkte (formal)

Hier ist $1-\left(\frac{1}{e}\right)^-$ minimal kleiner als $1-\frac{1}{e}$ .

Diese kleine Abweichung wird die ganze Rechnung mitgezogen.

$\def\arraystretch{1.25} \begin{array}{l}f'\left({\left(1-\frac{1}{e}\right)}^-\right)\\= 2\left(\ln\left(\left(1-{\frac{1}{e}}^+ -1\right)^2\right)+2\right)\\= 2\left(\ln\left({\frac{1}{e^2}}^-\right)+2\right)\\=2\underbrace{(\underbrace{-2\underbrace{\ln\left( e^-\right)}_{\lt 1}}_{\gt-2}+2)}_{\gt 0} \gt 0\end{array}$

Beachte, dass die kleine Abweichung je nach Klammersetzung und beim Quadrieren die Richtung ändert! Diese kleinliche und unanschauliche Vorgehensweise müsste man für jeden Punkt zwei mal durchführen. In der Schule reicht es meistens einfacher:

Da du ausgerechnet hast, dass es nur 2 Extrema gibt, muss der Graph dazwischen entweder die ganze Zeit steigen oder fallen (falls keine Polstelle dazwischen liegt!). Deshalb musst du nicht nicht so nahe an der Extremstelle die Steigung überprüfen - es reicht ein Punkt auf dem Weg zum nächsten Extremum.

Art der Extrempunkte (einfacher)

$\def\arraystretch{1.25} \begin{array}{l}f'\left(0\right)=2\left(\ln\left(\left(-1\right)^2\right)+2\right)=4>0\\f'\left(1\right)\rightarrow2\left(\ln\left(0^2\right)+2\right)=-\infty\end{array}$

Da $0 \lt 1-\frac{1}{e} \lt 1 \lt 1+\frac{1}{e}$ liegen die gewählten Punkte um das erste Extremum herum, aber noch vor dem zweiten Extremum.

Da es keine Polstellen gibt, brauchst du dir um die keine Sorgen zu machen.

$\displaystyle\Rightarrow\mathrm{HP}\left(1-\frac1{e}\left|\frac4{ e}\right)\right.$

$\def\arraystretch{1.25} \begin{array}{l} f'\left(1\right)\rightarrow2\left(\ln\left(0^2\right)+2\right)=-\infty \lt 0\end{array}$

$\displaystyle\Rightarrow\mathrm{TP}\left(1+\frac1{ e}\left|-\frac{4}{ e}\right)\right.$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Bestimme das Monotonieverhalten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten

Eine Funktion kann entweder streng monoton steigen oder fallen.

Das Monotonieverhalten ändert sich an den Minima und Maxima und es kann sich an den Definitionslücken ändern, wenn es Polstellen sind.

In den Intervallen zwischen diesen Punkten ist die Funktion stetig und hat dasselbe Monotonieverhalten.

Man kann alle kritischen Punkte nacheinander abarbeiten.

$x_\mathrm{Mon}$	$-\infty$	$-1$	$1-\frac{1}{e}$	$1$	$1+\frac{1}{e}$	$\infty$
$\displaystyle\lim_{x\rightarrow x_\mathrm{Mon}}f(x)$	$-\infty$	$-4\ln(4)$	$\frac{4}{e}$	$0$	$-\frac{4}{e}$	$\infty$

Zwischen diesen Punkten ist die Funktion jeweils streng monoton. Ob die Funktion fällt oder steigt sieht man an den Grenzwerten.

$x_\mathrm{Mon}$	$-\infty$		$-1$		$1-\frac{1}{e}$		$1$		$1+\frac{1}{e}$		$\infty$
$\displaystyle\lim_{x\rightarrow x_\mathrm{Mon}}f(x)$	$-\infty$		$-4\ln(4)$		$\frac{4}{e}$		$0$		$-\frac{4}{e}$		$\infty$
		$\nearrow$		$\nearrow$		$\searrow$		$\searrow$		$\nearrow$
		steigend		steigend		fallend		fallend		steigend

Diese Beobachtungen kann man noch mit Intervallen angeben.

Die Funktion $f$ ist…

…monoton steigend für $\displaystyle x\in \left] -\infty;1-\frac{1}{e}\right[\setminus\left\{-1\right\} \cup\left]1+\frac{1}{e};\infty \right[$ .

monoton fallend für $\displaystyle x \in \left]1-\frac{1}{e};1+\frac{1}{e}\right[\setminus\left\{1\right\}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechne die Wendepunkte.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte
Wendepunkte geben Änderungen der Krümmung des Funktionsgraphen an. Rechtsgekrümmte Graphen verlaufen in einer Rechtskurve, linksgekrümmte Graphen in einer Linkskurve.
Ändert sich dieses Verhalten, dann liegt ein Wendepunkt oder eine Definitionslücke im Kurvenverlauf vor.
Die Krümmung eines Graphen wird durch die 2. Ableitung beschrieben.
Da sich bei einem Wendepunkt die Krümmung ändert ist sie am Punkt selber quasi nicht vorhanden, also 0.
Zur Bestimmung der Lage der Wendepunkte musst du also die 2. Ableitung gleich 0 setzen.
Lage der Wendepunkte
Bisher bekannt sind die Funktion und die 1. Ableitung:
$\def\arraystretch{1.25} \begin{array}{l} f\left( x\right)=2\left( x-1\right)\ln\left(\left( x-1\right)^2\right)\\f'\left( x\right)=2\left(\ln\left(\left( x-1\right)^2\right)+2\right)\end{array}$
Für die 2. Ableitung musst du die 1. Ableitung nochmal ableiten.
Diesmal reicht die Anwendung der Kettenregel aus.
$\displaystyle f''\left( x\right)=2\frac{2\left( x-1\right)}{\left( x-1\right)^2}=\frac{4}{ x-1}$
Nun musst du noch die 2. Ableitung gleich 0 setzen.
Da der Zähler aber immer von 0 verschieden ist, wird auch die zweite Ableitung nie 0. Deshalb gibt es keine Wendepunkte.
Bemerkung: Das bedeutet nicht, dass sich die Krümmung nicht ändert. Wie du später sehen wirst ändert sich die Krümmung des Graphen nämlich doch einmal. An dieser Stelle ist nur kein Wendepunkt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme das Krümmungsverhalten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Krümmungsverhalten

Das Krümmungsverhalten ist eine Eigenschaft der Funktion, die angibt, in welche Richtung sich der Graph bewegt, bzw. welche Kurve er beschreibt.

Das Krümmungsverhalten ändert sich an allen Wendepunkten und es kann sich an allen Definitionslücken ändern.

Diese Punkte musst du nacheinander betrachten. Dabei kannst du ausnutzen, dass das Krümmungsverhalten sich wie das Monotonieverhalten der Ableitung verhält:

$x_\mathrm{Krümm}$	$-\infty$		$-1$		$1$		$\infty$
$\displaystyle \lim_{x\rightarrow x_\mathrm{Krümm}} f'(x)$	$\infty$		$2\ln(4)+4$		$-\infty$		$\infty$
Steigung von $f'$		$\searrow$		$\searrow$		$\nearrow$
Krümmung von $f$		rechtsgekrümmt		rechtsgekrümmt		linksgekrümmt

Du kannst auch mit der 2. Ableitung arbeiten. Dabei setzt du immer einen beliebigen Punkt zwischen den Intervallgrenzen in die 2. Ableitung ein. Ist das Ergebnis positiv, dann ist der Graph der Funktion in dem Intevall, aus dem der Punkt ist linksgekrümmt.

Ist es negativ, dann ist der Graph der Funktion dort rechtsgekrümmt.

Auch hier kann man wieder die Intervalle angeben.

Die Funktion $f$ ist

rechtsgekrümmt für $x \in \left]-\infty;1\right[\setminus \left\{-1\right\}$ .

linksgekrümmt für $x \in \left]1;\infty\right[$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechne den Wertebereich.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Der Wertebereich oder die Wertemenge einer Funktion ist die Menge aller Zahlenwerte, die die Funktion mindestens einmal annimmt.
Ist die Funktion in einem Intervall stetig, dann ist dort auch der Wertebereich ein Intervall.
Grenzen des Wertebereichs
Die Grenzen des Wertebereichs sind der minimale Wert und der maximale Wert, den die Funktion annimmt.
Diese Werte erhältst du entweder aus den Grenzwerten oder den Extremwerten.
$\mathrm{HP}(1-\frac1{e}|\frac4{ e})\Rightarrow y_{max}=\frac 4e$
$\mathrm{TP}(1+\frac{1}{e}|-\frac{4}{e})\Rightarrow y_{\min}=-\frac{4}{e}$
Das wären die $y$ -Werte des Minimums und des Maximums. Das sind aber nicht die kleinst- und größtmöglichen Werte, denn…
$\displaystyle \lim_{x\rightarrow -\infty}f(x)=-\infty \Rightarrow y_\mathrm{min}=-\infty$
$\displaystyle \lim_{x\rightarrow \infty}f(x)=\infty \Rightarrow y_\mathrm{max}=\infty$
…der Grenzwert im Unendlichen erlaubt Werte im Unendlichen.
Lücken im Wertebereich
Genauso wie es Definitionslücken gibt, können an diesen Unstetigkeitsstellen auch Lücken im Wertebereich auftreten. Die musst du noch überprüfen, um den Wertebereich angeben zu können.
Bei der Grenzwertbetrachtung wurde berechnet:
$\displaystyle\lim_{x\rightarrow-1} f\left( x\right)=-4\cdot\ln\left(4\right)$
Dieser Wert ist vom Wertebereich ausgenommen, wenn er nicht an einer anderen Stelle doch noch angenommen wird. Das musst du noch prüfen.
Da die Funktion von $-\infty$ kommt und das Maximum bei $x=1-\frac{1}{e}$ liegt, steigt die Funktion im Bereich um -1.
Im weiteren Funktionsverlauf fällt die Funktion dann nur noch einmal nämlich auf das Minimum $y=-\frac{4}{e}$ das höher liegt als $-4\ln(4)$ Also wird dieser Wert nicht mehr angenommen und ist eine Lücke im Wertebereich.
$\displaystyle\lim_{ x\rightarrow1} f\left( x\right)=0$
Der Wert 0 wird von der Funktion aber schon noch zweimal angenommen (die beiden Nullstellen) und ist daher keine Lücke im Wertebereich.
$\Rightarrow \mathbb{W}_\mathrm f=\mathbb{R}\setminus\left\{-4\cdot\ln\left(4\right)\right\}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichne den Graph.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graphen zeichnen
Wenn du den Funktionsgraphen zeichnen sollst, musst du alle Größen einzeichnen, die du zuvor ausgerechnet hast.
Wenn alles richtig ausgerechnet wurde, dann kannst du auch den Graphen sinnvoll zeichnen.
In dieser Zeichnung sind eingetragen:
Definitionslücken: $A\;\left(-1\left|-4\cdot\ln\left(4\right)\right)\right.,B\;\left(1\left|0\right)\right.$
Nullstellen: ${\mathrm{Nst}}_1\left(0\left|0\right)\right., \mathrm{Nst}_2\left(2\left|0\right)\right.$
Extrempunkte: $\mathrm{HP}\;\left(1-\frac1{ e}\left|\frac4{ e}\right)\right., \mathrm{TP}\left(1+\frac1{ e}\left|-\frac4{ e}\right)\right.$
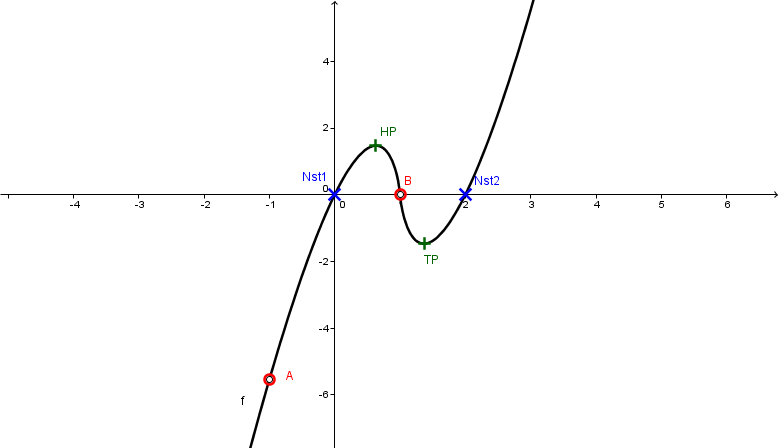
Bemerkungen:
Der nicht vorhandene Wendepunkt würde sich im Punkt $B$ befinden (Der Graph macht davor eine Rechtskurve und danach eine Linkskurve). Der Punkt $B$ ist aber eine Definitionslücke.
Am Punkt $B$ gehört die x-Achse des Koordinatensystems natürlich eigentlich durchgezeichnet. Der weiße Fleck dient zur Verdeutlichung der Definitionslücke.
Auch die Grenzwerte sind hier abzulesen: Richtung $+\infty$ geht auch der Graph nach $+\infty$ und Richtung $-\infty$ gegen $-\infty$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Überprüfe das Symmetrieverhalten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrieverhalten
Es gibt zwei Arten von Symmetrie: Achsensymmetrie und Punktsymmetrie
Für einen zu einer Achse $x = c$ achsensymmetrischen Graphen gilt $f\left( c+ x\right)= f\left( c- x\right)$ Gewöhnlich überprüft man nur Achsensymmetrie zur y-Achse mit $x = 0$ , also $f\left(x\right)= f\left(- x\right)$
Für einen zum Punkt $(c | d)$ punktsymmetrischen Graphen gilt $d- f\left( c- x\right)= -d+ f\left( c+ x\right)$ Gewöhnlich überprüft man nur Punktsymmetrie zum Ursprung $(0 | 0)$ , also $- f\left( x\right)= f\left(- x\right)$
Da man nicht alle Punkte und Achsen überprüft werden können, prüft man nur Ursprung und y-Achse.
Dabei beginnt man mit $f ( - x )$ und vergleicht das Aussehen dieser Funktion mit $f ( x )$ und $- f ( x )$ .
Symmetrie zum Ursprung / zur y-Achse
$\def\arraystretch{1.25} \begin{array}{rcl} f\left(- x\right)&=&2\left(- x-1\right)\cdot\ln\left(\left(- x-1\right)^2\right)\\&=&-2\left(x+1\right)\cdot\ln\left(\left( x+1\right)^2\right)\end{array}$
aber
$\def\arraystretch{1.25} \begin{array}{rcl} -f\left(x\right)&=&-2\left(x-1\right)\cdot\ln\left(\left( x-1\right)^2\right) \neq f(-x)\\ f(x)&=&2\left(x-1\right)\cdot\ln\left(\left( x-1\right)^2\right)\neq f(-x) \end{array}$
Deshalb keine Symmetrie zu Ursprung oder y-Achse
Symmetrie zum vermuteten Symmetriezentrum
Soll man aber die Symmetrie zu einem gegebenen Punkt überprüfen oder mit dem Funktionsgraphen das Symmetriezentrum bestimmen, dann kann man auch die allgemeine Formel anwenden müssen.
Mit dem groben Bild des Funktionsgraphen aus der vorigen Aufgabe im Hinterkopf, vermutest du, dass der Graph punktsymmetrisch zum Punkt $( 1 | 0 )$ sein könnte. Das überprüfst du jetzt.
$-f\left(1- x\right)=-2\left(1- x-1\right)\cdot\ln\left(\left(1- x-1\right)^2\right)=2 x\cdot\ln\left( x^2\right)$
und
$f\left(1+x\right)=2\left(1+x-1\right)\cdot\ln\left(\left(1+x-1\right)^2\right)=2x\cdot\ln\left(x^2\right)$
Die beiden Ausdrücke sind identisch, was auf Punktsymmetrie zum Punkt $( 1 | 0 )$ schließen lässt.
Jetzt sind wir aber noch nicht fertig. Sehen wir uns den Graphen nochmal an, dann erkennen wir, dass die linke Seite bei x = -1 eine Lücke im Graphen hat, die die rechte Seite nicht hat. Der Graph deckt sich also bei einer Spiegelung nicht immer auf sich selbst. Deshalb keine Symmetrie!
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme die Tangente zur Funktion $f$ am allgemeinen Punkt $(p|f(p))$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangenten

Die Tangente zum Punkt $(p|f(p))$ ist eine Gerade, die den Graph $G_f$ von $f$ bei $(p|f(p))$ berührt.

Sie hat also das Aussehen einer Geradengleichung $y=mx+t$ .

Da die Tangente den Graphen von $f$ berührt, läuft sie an genau dem einen Berührpunkt quasi parallel zu $G_f$ , hat also die gleiche Steigung. Damit kannst du etwas anfangen:

$y=mx+ t$

Das ist die allgemeine Geradengleichung. Für die Tangentengleichung musst du nun $m$ und $t$ bestimmen.

Da, wie oben beschrieben, die Steigung der Tangente am Berührpunkt gleich der Steigung des Funktionsgraphen ist, kannst du die beiden Terme gleichsetzen.

$m= f'\left( p\right)=2\cdot\left(\ln\left(\left( p-1\right)^2\right)+2\right)$

Für das fehlende $t$ benötigst du den Berührpunkt $(p|f(p))$ .

Für diesen ist die Gleichung nämlich auch erfüllt. Deshalb kannst du den Punkt für $x$ und $y$ einsetzen und kannst die letzte Unbekannte $t$ bestimmen

$\displaystyle f\left(p\right)$	$=$	$\displaystyle f'\left(p\right)\cdot p+t$
$\displaystyle 2\cdot\left(p-1\right)\ln\left(\left(p-1\right)^2\right)$	$=$	$\displaystyle 2\cdot\left(\ln\left(\left(p-1\right)^2\right)+2\right)\cdot p+t$
	↓	Bringe t auf eine Seite der Gleichung.
$\displaystyle t$	$=$	$\displaystyle 2\left(p-1\right)\ln\left(\left(p-1\right)^2\right)-2\left(\ln\left(\left(p-1\right)^2\right)+2\right)p$
$\displaystyle t$	$=$	$\displaystyle 2\cdot\ln\left(\left(p-1\right)^2\right)\cdot\left(\left(p-1\right)-p\right)-4p$
$\displaystyle t$	$=$	$\displaystyle -2\cdot\ln\left(\left(p-1\right)^2\right)-4p$

Als allgemeine Tangentengleichung erhältst du also:

$y=2\left(\ln\left(\left( p-1\right)^2\right)+2\right)\cdot x-2\cdot\ln\left(\left( p-1\right)^2\right)-4 p$

Bemerkungen:

Auch wenn diese Gleichung unschön aussieht: Für ein konkretes $p$ wird die Gleichung kürzer und viel schöner und da du sie allgemein ausgerechnet hast, kann man jeden Punkt $(p|f(p))$ ohne Bedenken einsetzen.
Auch die Tangenten sind natürlich nur dann definiert, wenn auch die Funktion f definiert ist. Allerdings sehen die Tangenten zur Funktion $\widehat{f}$ genau gleich aus!

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Bestimme die Schnittpunkte des Funktionsgraphen $G_f$ von $f$ mit dem Funktionsgraphen $Gg$ von der Funktion

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionsgraphen
Wenn sich zwei Graphen schneiden, dann liefern beide Funktionen an den Schnittpunkten das gleiche Ergebnis. Die Funktionswerte sind an diesen Punkten identisch.
x- Werte bestimmen
Zur Bestimmung der Schnittpunkte reicht es also, die Funktionen gleich zu setzen und nach $x$ aufzulösen, da man dann die $x$ -Werte erhält, für die die Funktionen dasselbe Ergebnis liefern.
Du setzt an:
$\def\arraystretch{1.25} \begin{array}{rcl} f\left( x\right)&=& g\left( x\right)\\2\left( x-1\right)\ln\left(\left( x-1\right)^2\right)&=&2\left( x-1\right)\ln\left( x\right)\end{array}$
Auf beide Seiten stehen Produkte mit dem gleichen Faktor $2(x-1)$ . Falls dieser Faktor nicht 0 ist, darfst du durch ihn dividieren.
Du machst eine Fallunterscheidung:
Fall 1: $2\left(\mathrm x-1\right)\neq0:$
$\def\arraystretch{1.25} \begin{array}{rcll}\ln\left(\left( x-1\right)^2\right)&=&\ln\left( x\right)&\vert e\\\left( x-1\right)^2&=& x&\\x^2-2x+1&=& x&\vert- x\\x^2-3 x+1&=&0&\end{array}$
Im ersten Fall erhältst du eine quadratische Gleichung, die du nun mit der Mitternachtsformel lösen kannst.
$\def\arraystretch{2} \begin{array}{ccc}{ x}_{1;2}&=&\dfrac{- b\pm\sqrt{ b^2-4{ac}}}{2 a}\\&=&\dfrac{3\pm\sqrt{9-4}}2\end{array}$
$\Rightarrow{ x}_1=\frac12\left(3+\sqrt5\right)$ und $x_2=\frac12\left(3-\sqrt5\right)$
Mit der Mitternachtsformel erhältst du die $x$ -Werte von zwei Schnittpunkten.
Nun muss aber noch der 2. Fall betrachtet werden!
Fall 2: $2\left(\mathrm{x}-1\right)=0$
$\def\arraystretch{1.25} \begin{array}{rrcl}&2\left(\mathrm x-1\right)&=&0&\\\Leftrightarrow&\mathrm x&=&1&\notin\mathbb{D}_ f\end{array}$
Fall 2 tritt nur ein, wenn $x=1$ gilt. Da 1 nicht im Definitionsbereich liegt, kann auch dieser Fall nicht eintreten und du bist fertig.
y-Werte bestimmen
Um die Schnittpunkte angeben zu können, muss man sowohl $x$ - als auch $y$ - Werte kennen. Du setzt deshalb die gefundenen $x$ -Werte noch in eine Funktion ein und erhältst die gesuchten $y$ -Werte.
Da du Schnittpunkte berechnest, sind die Funktionswerte bei beiden Funktionen gleich - du wählst also am besten die einfachere.
$\def\arraystretch{1.25} \begin{array}{rcl} g\left(\frac{1}{2}\left(3+\sqrt{5}\right)\right)&=&2\left(\frac{1}{2}\left(3+\sqrt{5}\right)-1\right)\ln\left(\frac{1}{2}\left(3+\sqrt5\right)\right)\\&=&\left(1+\sqrt{5}\right)\ln\left(\frac{1}{2}\left(3+\sqrt{5}\right)\right)\end{array}$
$\def\arraystretch{1.25} \begin{array}{rcl}g\left(\frac{1}{2}\left(3-\sqrt{5}\right)\right)&=&2\left(\frac{1}{2}\left(3-\sqrt5\right)-1\right)\ln\left(\frac{1}{2}\left(3-\sqrt{5}\right)\right)\\&=&\left(1-\sqrt{5}\right)\ln\left(\frac{1}{2}\left(3-\sqrt{5}\right)\right)\end{array}$
Die Ergebnisse sind nicht schön, aber genau und richtig. Du hast also die Schnittpunkte $S_1$ und $S_2$ bestimmt:
$\displaystyle S_1 \left(\frac{1}{2}\left(3+\sqrt{5}\right) \left| \left(1+ \sqrt{5} \right) \ln \left(\frac{1}{2}\left(3+\sqrt{5}\right)\right)\right)\right.\\ \;\\ S_2 \left(\frac{1}{2}\left(3-\sqrt{5}\right) \left| \left(1- \sqrt{5} \right) \ln \left(\frac{1}{2}\left(3-\sqrt{5}\right)\right)\right)\right.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Stammfunktion.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Um eine Stammfunktion für $f$ zu finden muss man die Funktion $f$ integrieren . Bei komplizierteren Funktionen kann das schwierig werden, aber bei der Integration gibt es Techniken, die es auch erlauben, solche Funktionen zu integrieren, z.B. Substitution und Partielle Integration
$F\left( x\right)=\int f\left( t\right)\mathrm{d}t$
Zuerst stellst du die Gleichung für das Integral auf.
$F(x)$ ist dabei die gesuchte Stammfunktion zu $f$ .
Dann setzt man die Funktion $f$ ein.
Es gibt zwei Wege, um das Integral zu lösen.
Version 1: Partielle Integration
$F\left( x\right)=\int2\left( t-1\right)\cdot\ln\left(\left( t-1\right)^2\right){d}t$
Hier habst du ein Produkt, das sich nicht ohne Weiteres integrieren lässt. Versuch es mit partieller Integration, wobei
$u'(x)=2(x-1) \wedge v(x)=\ln\left((x-1)\right)$ .
$\def\arraystretch{2} \begin{array}{rcl} F\left( t\right)&=&\int u'\left( t\right) v\left( t\right)\mathrm{d}t\\&=& u\left( x\right) v\left( x\right)-\int u\left( t\right) v'\left( t\right)\mathrm{d}t\\&=&\left( x-1\right)^2\ln\left(\left( x-1\right)^2\right)-\int\left( t-1\right)^2\frac{2\left( t-1\right)}{\left( t-1\right)^2}{d}t\\&=&…\end{array}$
Dass $(x-1)^2$ eine mögliche Stammfunktion von $2(x-1)$ ist, kann man durch Ableiten der Stammfunktion überprüfen.
Eigentlich wäre $\int 2(t-1)\mathrm{d}t=x^2-2x$ , da man aber bei Stammfunktionen Konstanten beliebig addieren kann kommt man auch auf das schönere $x^2-2x+1=(x-1)^2$ .
Im neuen Integral kürzt sich dann einiges weg…
$\def\arraystretch{2} \begin{array}{cl}=\left( x-1\right)^2\ln\left(\left( x-1\right)^2\right)-\int 2\left( t-1\right){d}t\\=\left( x-1\right)^2\ln\left(\left( x-1\right)^2\right)-\left( x-1\right)^2+ C\\=\left( x-1\right)^2\cdot\left(\ln\left(\left( x-1\right)^2\right)-1\right)+ C\end{array}$
(mit einer Konstanten $C$ )
…bis auf das bereits bekannte Integral von $2(x-1)$ .
Nachdem das letzte Integral bestimmt ist, dürfen wir nicht vergessen, eine Konstante C zu addieren, die möglicherweise vorhanden, aber nicht auffällt, weil sie beim Ableiten sofort wegfällt.
$\Rightarrow F\left( x\right)=\left( x-1\right)^2\cdot\left(\ln\left(\left( x-1\right)^2\right)-1\right)+ C$
Wird nur verlangt, dass man eine Stammfunktion angeben soll, dann kann man auch $C=0$ setzen und die Konstante weglassen.
Version 2: Substitution
$F\left( x\right)=\int2\left( t-1\right)\cdot\ln\left(\left( t-1\right)^2\right)\mathrm{d}t$
Für eine Substitution benötigst du ein Integral der Form
$\displaystyle \int g'(t)f(g(t))\mathrm{d}t$ .
Genau das liegt aber vor. Wir wählen
$f(x)=\ln x$ und $g(x)=(x-1)^2=z$ .
$\def\arraystretch{2} \begin{array}{ccc} F\left( x\right)&=&\int2\left( t-1\right)\cdot\ln\left(\left( t-1\right)^2\right)\mathrm{d}t\\ F\left( z\right)&=&\int\ln\left( z\right)\mathrm{d}z\\ &=& z\left(\ln\left( z\right)-1\right)+ D \end{array}$
Da du ein unbestimmtes Integral hast, kannst du die Integrationsgrenzen natürlich nicht anpassen.
Die Stammfunktion des Logarithmus solltest du aus der Schule kennen, kurz irgendwo nachschlagen oder aber nochmal mit partieller Integration nachrechnen.
Nun musst du nur noch resubstituieren.
$z=(x-1)^2$
$\Rightarrow F\left( x\right)=\left( x-1\right)^2\left(\ln\left(\left( x-1\right)^2\right)-1\right)+ C$
Schon bist du fertig. Das zeigt wieder: Wenn du bestimmte Eigenarten von Funktionen siehst, kannst du dir einiges an Arbeit sparen.
Beachte: Die Stammfunktion ist nur auf stetigen Abschnitten der Ausgangsfunktion $f$ definiert, also nicht auf den Definitionslücken -1 und 1 !
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Größe der Fläche zwischen dem Graphen der Funktion $f$ , der x-Achse und den Geraden $x=-0{,}5$ und $x=0{,}5$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integration
Zur Berechnung der Fläche unter dem Graphen zwischen zwei bestimmten Stellen muss man die Funktion von der linken Grenze bis zur rechten Grenze integrieren. Dabei darf die Funktion zwischen den Grenzen die x-Achse nicht schneiden, da sich sonst die Flächen unter und über der x-Achse wieder gegenseitig wegheben können.
Wenn die Funktion eine Nullstelle im Integrationsintervall hat muss man zuerst bis zur Nullstelle integrieren und dann von der Nullstelle aus weiter, da man nur positive Flächen betrachtet.
$\def\arraystretch{2} \begin{array}{rcl} A&=&\left|\int_{-0{,}5}^{0{,}5}\left| f\left( x\right)\right|\operatorname{d} x\right|\\&=&\left|\int_{-0{,}5}^0 f\left( x\right)\operatorname{d} x+\int_0^{0{,}5} f\left( x\right)\operatorname{d} x\right|\\&=&\vert F\left(0\right)- F\left(-0{,}5\right)+ F\left(0{,}5\right)- F\left(0\right)\vert\\&=&\vert-1-0{,}25\cdot\left(\ln\left(2{,}25\right)-1\right)+0{,}25\cdot\left(\ln\left(0{,}25\right)-1\right)+1\vert\\&=&\left|0{,}25\left(\ln\left(0{,}25\right)-\ln\left(2{,}25\right)\right)\right|\\&=&\left|0{,}25\cdot\ln\left(\frac{0{,}25}{2{,}25}\right)\right|\\&=&\left|0{,}25\cdot\ln\left(\frac19\right)\right|\\&\approx&0{,}55\end{array}$
Die Fläche berechnet sich also als der Betrag des Integrals der positiven Funktion von -0,5 bis 0,5.
Spaltet man das Integral an der Nullstelle 0 auf und verwendet die Stammfunktion, dann braucht man nur die Grenzen einzusetzen und zu vereinfachen.
Je nachdem, wie es verlangt wird, kann man das Ergebnis auch als genauen Wert stehen lassen und muss den Logarithmus nicht mehr ausrechnen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Größe der Fläche die der Graph der stetigen Funktion $\widehat{f}$ mit dem Graphen der Tangente von $\widehat{f}$ am Punkt $\displaystyle \left(1-\frac{1}{e}\left|\frac{4}{e}\right)\right.$ einschließt.
Hinweis: Runde die Integrationsgrenzen und das Ergebnis auf zwei Nachkommastellen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integration
Will man die Fläche zwischen zwei Graphen berechnen, so berechnet man zuerst die Fläche unter den "höheren" Graphen und zieht dann die Fläche unter dem "tieferen" Graphen ab.
Da sich die Lage zueinander bei jedem Schnittpunkt ändert muss man zuerst die Schnittpunkte der beiden Graphen kennen:
Schnittpunkte der Graphen
Du kannst hier entweder die Tangentengleichung am Punkt $\displaystyle\left(1-\frac{1}{e}\left|\frac{4}{e}\right)\right.$ aufstellen und damit arbeiten oder du erinnerst dich, dass $\displaystyle\left(1-\frac{1}{e}\left|\frac{4}{e}\right)\right.$ der Hochpunkt von $f$ war.
Deshalb hat die Tangente $t_\mathrm{HP}$ an diesem Punkt die Steigung 0 und lautet:
$t_\mathrm{HP}: y=\frac{4}{e}$
Mit diesem Wissen hast du auch schon den ersten Schnittpunkt gefunden Es ist der Hochpunkt $\mathrm{HP}\left(1-\frac{1}{e}\left|\frac{4}{e}\right)\right.$ .
Für die anderen Schnittpunkte musst du nun beide Funktionen gleichsetzen:
$\widehat{ f}\left( x\right)=\frac{4}{e}$
Sei $x\neq-1;1$
$2\left(x-1\right)\ln\left(\left(x-1\right)^2\right)=\frac{4}{e}$
Da diese Gleichung nicht exakt lösbar ist, hilft das Newton'sche Näherungsverfahren bei der Funktion
Überprüfst du den Funktionsgraphen, dann stellst du fest, dass es nur einen zweiten Schnittpunkt gibt. Dieser liegt zwischen den Werten 2 und 3. Wir wählen $x_0=3$ .
$\def\arraystretch{1.25} \begin{array}{ccl}{x}_1&=&{x}_0-\frac{\widetilde{f}\left({x}_0\right)}{\widetilde{f'}\left({x}_0\right)}\\&=&3-\frac{4\ln\left(4\right)-\frac4{e}}{2\left(\ln\left(4\right)+2\right)}\approx2{,}40\end{array}$
Der erste Newtonschritt liefert als neuen Ausgangswert ungefähr 2,40.
Der Wert liegt links von 3 auf der Seite der Nullstelle von $\widetilde{f}$ , die ja der Schnittpunkt ist.
Weitere Newtonschritte liefern
$\def\arraystretch{1.25} \begin{array}{l}{x}_2={x}_1-\frac{\widetilde{f}\left({x}_1\right)}{\widetilde{f'}\left({x}_1\right)}=2{,}32\\{x}_3={x}_2-\frac{\widetilde{f}\left({x}_2\right)}{\widetilde{f'}\left({x}_2\right)}=2{,}32\end{array}$
Das Newtonverfahren konvergiert also sehr schnell gegen einen Wert.
Überprüfst du diesen Wert durch Einsetzen in $f$ , erhältst du $f(2{,}32)\approx1{,}47\approx\dfrac{4}{e}$ . Das Ergebnis stimmt also im Rahmen der Rechenungenauigkeit.
Das Integral zur Flächenbestimmung geht also von $1-\dfrac{1}{e}$ bis $2{,}32$ .
Flächenberechnung
Die Fläche zwischen zwei Graphen berechnet sich über die Differenz der Flächen unter den einzelnen Integralen.
$\def\arraystretch{2} \displaystyle\begin{array}{ccc} A&=&\int_{1-\frac1{ e}}^{2{,}32}{t}_{HP}\left(x\right)\mathrm{d}x-\int_{1-\frac1{e}}^{2{,}32}\widehat{f}\left(x\right)\operatorname{d}x\\&=&\int_{1-\frac1{e}}^{2{,}32}\frac{4}{e}\mathrm{d}x-\int_{1-\frac1{ e}}^{2{,}32}2\left(\mathrm x-1\right)\ln\left(\left(\mathrm x-1\right)^2\right)\operatorname{d}x\\&=&\left[\frac4{e}x\right]_{1-\frac1{e}}^{2{,}32}-F\left(2{,}32\right)+F\left(1-\textstyle\frac1{e}\right)\\&\approx&3{,}41-0{,}93+0{,}77-0{,}41\\&\approx&2{,}8\end{array}$
(Man kann hier auf die Stammfunktion von $f$ zurückgreifen, die dieselbe ist, wie die von $\widehat{f}$ , aber überall definiert ist.
Integriert man die Konstante und setzt man die Grenzen ein, so erhält man einen ungefähren Wert für die gesuchte Fläche.)
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne den Umfang und den Flächeninhalt des Vierecks $\mathrm{Nst}_1\mathrm{TP}\mathrm{Nst}_2\mathrm{HP}$
Runde Zwischenergebnisse notfalls auf zwei Nachkommastellen.
Das ist keine typische Analysisaufgabe, sondern eher ein kurzer Abstecher in die Geometrie. Willst du nur Analysis üben, dann kannst du diese Aufgabe gerne ignorieren.
Was wir wissen
Die vier gegebenen Punkte sind die Nullstellen und die Extrema. Ihre Koordinaten lauten
${\mathrm{Nst}}_1\;\left(0\left|0\right)\right.,\mathrm{TP}\left(1+\frac{1}{ e}\left|-\frac{4}{e}\right)\right.,\mathrm{Nst}_2\left(2\left|;0\right)\right.,\mathrm{HP}\left(1-\frac{1}{e}\left|\frac{4}{e}\right)\right.$ .
Zusätzlich sind die Achsen des Koordinatensystems zueinander senkrecht, was die Bestimmung der Seitenlängen des Vierecks mittels Pythagoras ermöglicht.
Umfang
Bestimme die Längen der Seiten über Pythagoras:
$\overline{{\mathrm{Nst}}_1\mathrm{TP}}=\sqrt{\left(1+\frac1{e}\right)^2+\left(-\frac4{e}\right)^2}\approx2$
$\overline{{\mathrm{TPNst}}_2}=\sqrt{\left(2-\left(1+\frac1{\mathrm e}\right)\right)^2+\left(-\frac4{\mathrm e}\right)^2}\approx1{,}6$
$\overline{{\mathrm{Nst}}_2\mathrm{HP}}=\sqrt{\left(2-\left(1-\frac1{\mathrm e}\right)\right)^2+\left(\frac4{\mathrm e}\right)^2}\approx2$
$\overline{{\mathrm{HPNst}}_1}=\sqrt{\left(1-\frac1{\mathrm e}\right)^2+\left(\frac4{\mathrm e}\right)^2}\approx1{,}6$
Du stellst fest, dass jeweils zwei gegenüberliegende Seiten gleich lang sind. Das Vierecks ist also schlimmstenfalls ein Parallelogramm.
Der Umfang lässt sich aber jetzt schon berechnen:
$U_\mathrm{Viereck}\approx2+1{,}6+2+1{,}6=7{,}2$
Flächeninhalt
Um den Flächeninhalt eines Parallelogramms zu berechnen brauchen wir noch eine Größe, z.B. die Höhe.
Die Höhe zu bestimmen ist aber viel zu umständlich. Für die Flächenberechnung gibt es einfachere Wege:
Methode 1: Analytische Geometrie in der Ebene
Versuche einen Weg über die analytische Geometrie. Für die Fläche eines Paralellogramms gilt im $\mathbb{R}^2$ :
$A_▱=\left|\det\left(\overrightarrow{\mathrm{AB}};\overrightarrow{\mathrm{AD}}\right)\right|$
mit den aufspannenden Vektoren $\overrightarrow{\mathrm{AB}}$ und $\overrightarrow{\mathrm{AD}}$ .
In unserem Fall haben wir die Vektoren
$\overrightarrow{\mathrm{AB}}=\overrightarrow{{\mathrm{Nst}}_1\mathrm{TP}}=\begin{pmatrix}1+\frac{1}{e}\\-\frac{4}{e}\end{pmatrix},\overrightarrow{\mathrm{AD}}=\overrightarrow{{\mathrm{Nst}}_1\mathrm{HP}}=\begin{pmatrix}1-\frac{1}{e}\\\frac{4}{e}\end{pmatrix}$
$\def\arraystretch{1.25} \displaystyle\begin{array}{ccl} A_\mathrm{Viereck}&=&\left|\det\left(\vec{\mathrm{AB}};\vec{\mathrm{AD}}\right)\right|\\ &=&\left|\det\begin{pmatrix}1+\frac1{\mathrm e} &1-\frac4{e}\\ -\frac4{\mathrm e}&\frac4{\mathrm e}\end{pmatrix}\right|\\ &=&\left|\begin{pmatrix}\left(1+\frac1{\mathrm e}\right)\left(\frac4{\mathrm e}\right)-\left(1-\frac1{\mathrm e}\right)\left(-\frac4{\mathrm e}\right)\end{pmatrix}\right|\\&=&\begin{vmatrix}\frac8{\mathrm e}\end{vmatrix}\\ &=&\frac8{\mathrm e}\end{array}$
Somit hast du die Fläche des Vierecks berechnet.
Methode 2: Aufspalten in Dreiecke
Siehst du dir den Funktionsgraphen an, kannst du erkennen, dass das gesuchte Viereck durch die x-Achse in zwei Dreiecke aufgeteilt wird. Für die Dreiecksflächen brauchst du nur Grundseite und Höhe. Beides ist durch die Koordinaten gegeben.
Dreieck $\mathrm{Nst}_1\mathrm{Nst}_2\mathrm{HP}$ :
Grundseite: Subtrahiere die x-Koordinaten der Nullstellen: ${g}_1=2-0=2$
Höhe: Der Betrag der y-Koordinate des Hochpunktes: ${h}_1=\dfrac{4}{e}$
Dreieck $\mathrm{Nst}_1\mathrm{TP}\mathrm{Nst}_2$ :
Grundseite: Subtrahiere die x-Koordinaten der Nullstellen: $g_2=2-0=2$
Höhe: Der Betrag der y-Koordinate des Tiefpunktes: $h_2=\frac{4}{e}$
Fläche des Vierecks $\mathrm{Nst}_1\mathrm{TPNst}_2\mathrm{HP}$ :
$\displaystyle A_▱=\frac{1}{2}g _1 h_1+\frac{1}{2}g_2 h_2=\frac{1}{2}\cdot 2\cdot\frac{4}{e}+\frac{1}{2}\cdot2\cdot\frac{4}{e}=\frac{8}{e}$
Auch hier ergibt sich - sogar sehr schnell - die Vierecksfläche.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \frac{\left(2\mathrm{x}^2-2\right)\cdot\ln\left(\left(\mathrm{x}-1\right)^2\right)}{1+\mathrm{x}}$	$=$	$\displaystyle \frac{2\left(\mathrm x^2-1\right)\cdot\;\ln\left(\left(\mathrm x-1\right)^2\right)}{1+\mathrm x}$
	↓	Im Nenner kommt eine 3. binomische Formel vor. Forme diese um.
	$=$	$\displaystyle \frac{2\left(\left(\mathrm{x}-1\right)\left(\mathrm{x}+1\right)\right)\cdot\ln\left(\left(\mathrm{x}-1\right)^2\right)}{1+\mathrm{x}}$
	↓	Kürze $(1+x)$ .
	$=$	$\displaystyle 2\left(\mathrm{x}-1\right)\cdot\ln\left(\left(\mathrm{x}-1\right)^2\right)$

$\displaystyle f(x)$	$=$	$\displaystyle 0$
$\displaystyle 2\left( x-1\right)\ln\left(\left( x-1\right)^2\right)$	$=$	$\displaystyle 0$

Aufgaben zur Kurvendiskussion mit Exponentialfunktion und Logarithmus

Definitionsbereich

Der Nenner darf nicht Null werden.

Das Argument des Logarithmus muss größer als 0 sein.

Definitionsmenge

Art der Definitionslücken

Definitionslücke x=−1x=-1x=−1

Definitionslücke x=1x=1x=1

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Grenzwert im Unendlichen

Grenzwert an den Definitionslücken von beiden Seiten

Grenzwerte an x=−1x=-1x=−1

Grenzwerte an x=1x=1x=1

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Waagerechte Asymptoten

Senkrechte Asymptoten

Schiefe Asymptoten

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Extremstelle berechnen

Koordinaten der Extrempunkte

Art der Extrempunkte bestimmen

Art der Extrempunkte (formal)

Art der Extrempunkte (einfacher)

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lage der Wendepunkte

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Grenzen des Wertebereichs

Lücken im Wertebereich

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Symmetrie zum Ursprung / zur y-Achse

Symmetrie zum vermuteten Symmetriezentrum

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

x- Werte bestimmen

y-Werte bestimmen

Hast du eine Frage oder Feedback?

Version 1: Partielle Integration

Version 2: Substitution

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Schnittpunkte der Graphen

Flächenberechnung

Hast du eine Frage oder Feedback?

Was wir wissen

Umfang

Flächeninhalt

Methode 1: Analytische Geometrie in der Ebene

Methode 2: Aufspalten in Dreiecke

Hast du eine Frage oder Feedback?

Definitionslücke $x=-1$

Definitionslücke $x=1$

Grenzwerte an $x=-1$

Grenzwerte an $x=1$