Differenzierbarkeit ist eine Eigenschaft von Funktionen, die darüber Auskunft gibt, ob und wo sich eine Funktion ableiten lässt.
Eine Funktion heißt differenzierbar an einer Stelle ihres Definitionsbereichs, falls der Differentialquotient existiert:
Wir nennen dann diesen Grenzwert Ableitung an der Stelle .
Anschaulich bedeutet das, dass der Graph von an der Stelle eine eindeutige und nicht senkrechte Tangente besitzt. Der Grenzwert und damit die Ableitung gibt die Steigung dieser Tangente an.
Ist an jeder Stelle der Definitionsmenge differenzierbar, so nennt man differenzierbar.
Differenzierbarkeit überprüfen
Der obige Grenzwert existiert genau dann, wenn linksseitiger und rechtsseitiger Grenzwert des zugehörigen Differenzenquotienten existieren und übereinstimmen, d. h. wenn gilt:
Diese Äquivalenz ist insbesondere dann hilfreich, wenn die Differenzierbarkeit zusammengesetzter Funktionen an einer "Nahtstelle" überprüft werden soll.
Sind die Ableitungen links und rechts von bereits bekannt, kann die Differenzierbarkeit über die Gleichheit der Ableitungen nachgewiesen werden. Eine an der Stelle stetige Funktion ist also differenzierbar, wenn beide Grenzwerte existieren und gilt:
Nicht differenzierbare Funktionen
Differenzierbarkeit einer Funktion bedeutet, dass der Graph der Funktion an jeder Stelle eine eindeutig bestimmbare Tangente besitzt.
Im nebenstehenden Applet kannst Du die Punkte und auf dem Graphen von verschieben. An und sind die jeweiligen Tangenten abgetragen.
Du kannst über das Eingabefeld auch eine andere Funktion eingeben und diese graphisch auf Differenzierbarkeit untersuchen.
Ist eine Funktion an einer Stelle nicht differenzierbar, so ist die Tangente an dieser Stelle nicht bestimmbar. Dafür kann es verschiedene Gründe geben.
Besitzt der Graph an einer Stelle eine "Spitze", so kann man dort zwei unterschiedliche "Tangenten" konstruieren, eine "linksseitige Tangente" und eine "rechtsseitige Tangente". Aber eben keine eindeutige, "einzige" Tangente. Die Funktion ist an dieser Stelle nicht differenzierbar.
Du kannst die Punkte P und Q auf f verschieben. Beobachte, wie sich die Tangentensteigung an der "Spitze" verhält.
Du kannst auch andere Funktionen eingeben und graphisch auf Differenzierbarkeit untersuchen: z.B. ; Eingabe: .
Die durch gegebene Funktion ist ein weiteres Beispiel für eine nicht differenzierbare Funktion. Es gilt nämlich:
Somit ist nicht an der Stelle differenzierbar.
Du kannst die Punkte und auf verschieben. Beobachte, wie sich die Tangentensteigung an der Stelle verhält.
Du kannst auch andere Funktionen eingeben und graphisch auf Differenzierbarkeit untersuchen.
Differenzierbarkeit höherer Ordnungen
Wir betrachten eine differenzierbare Funktion . Ist ihre Ableitung ebenfalls differenzierbar, so heißt die Funktion zweimal differenzierbar. Analog lassen sich die Bezeichnungen dreimal / viermal / -mal differenzierbar definieren.
Eine differenzierbare Funktion, deren Ableitungsfunktion stetig ist, heißt stetig differenzierbar.
Differenzierbarkeit nachweisen
Der Differentialquotient lässt sich mit der h-Methode berechnen.
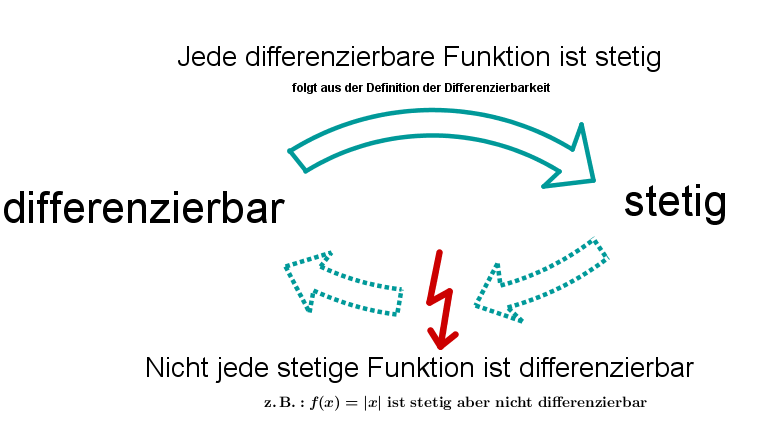
Zusammenhang zwischen Differenzierbarkeit und Stetigkeit
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Steigung und Differenzierbarkeit anhand des Graphen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
