Aufgaben zu Rechtecken und Quadraten
Ganz schön eckig! Hier findest du Aufgaben zu Rechtecken und Quadraten. Schaffst du sie alle?
- 1
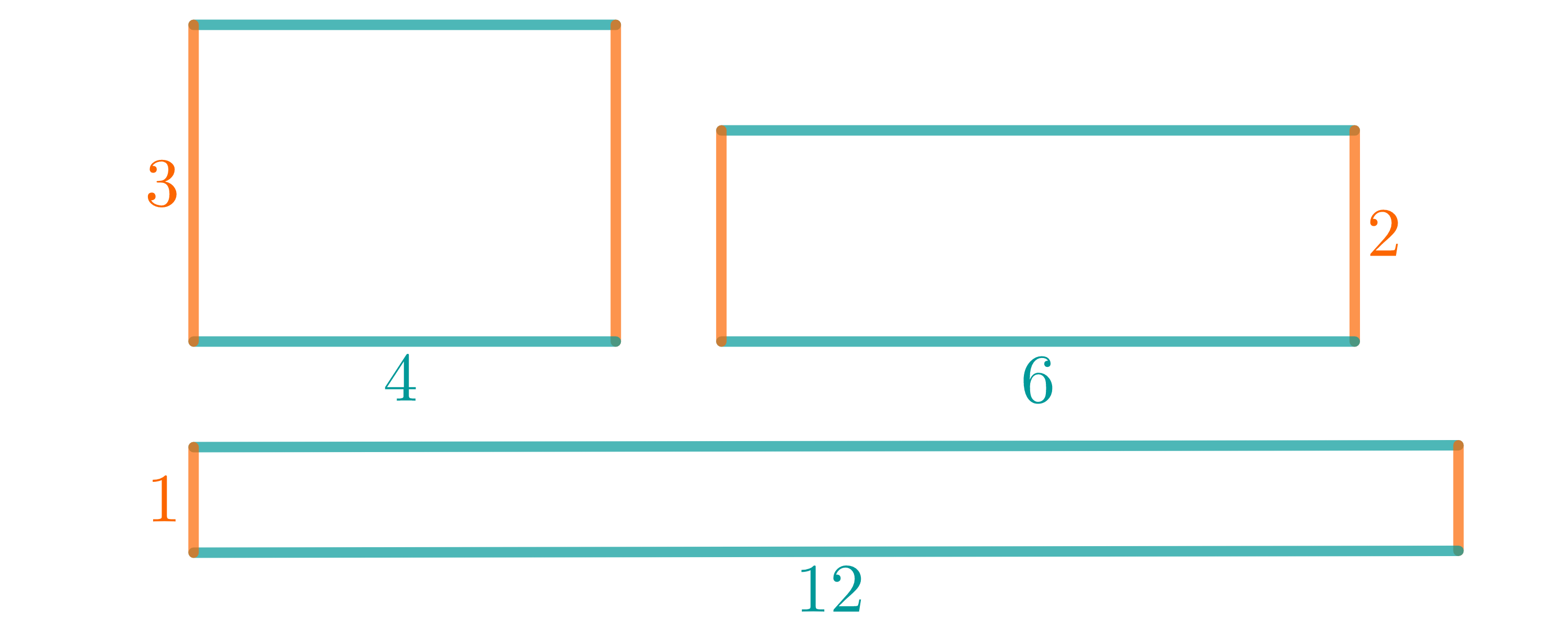
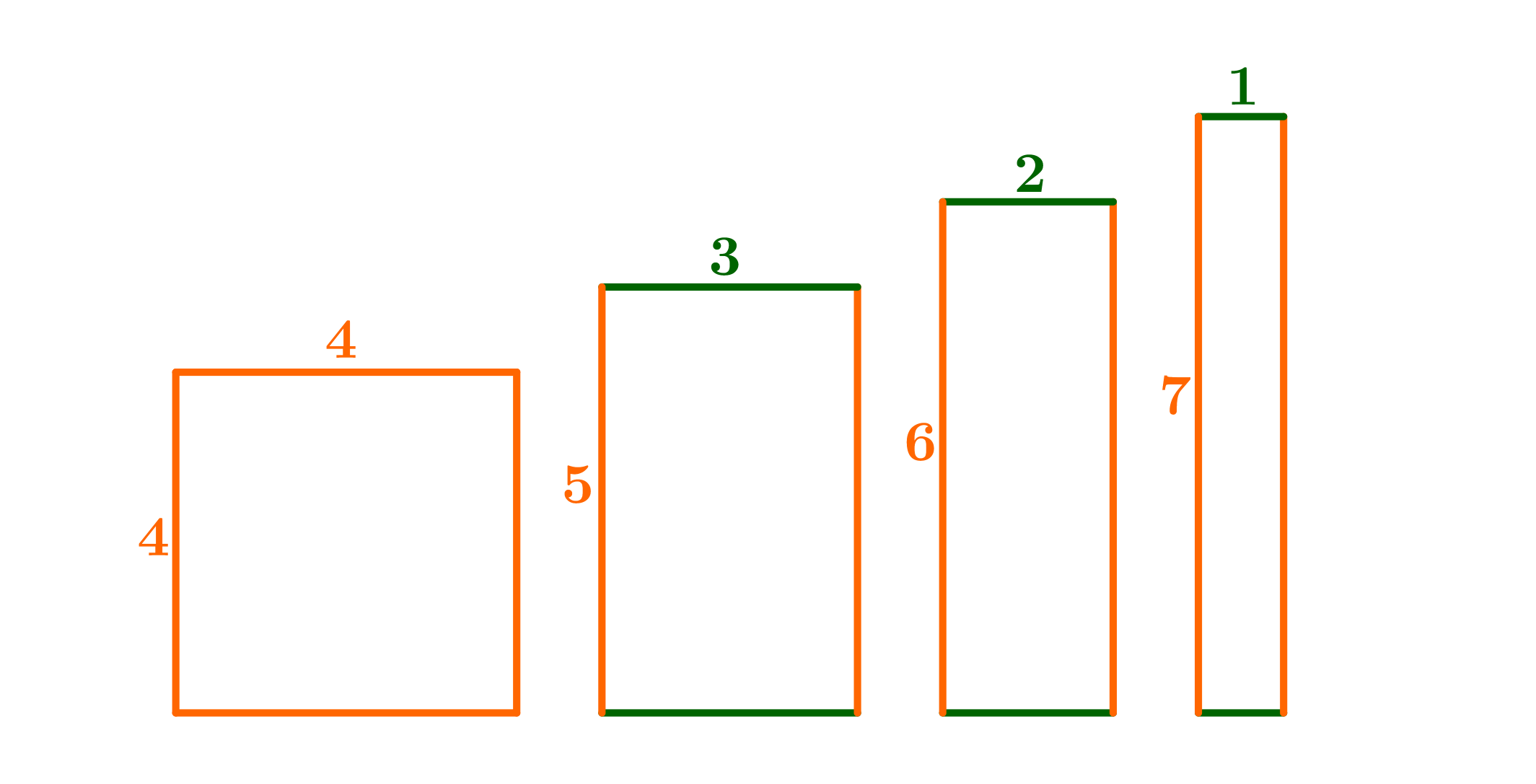
Welche der folgenden Vierecke sind Rechtecke?
- 2
Gib an, wie du den Umfang folgender Formen berechnen kannst.
Quadrat
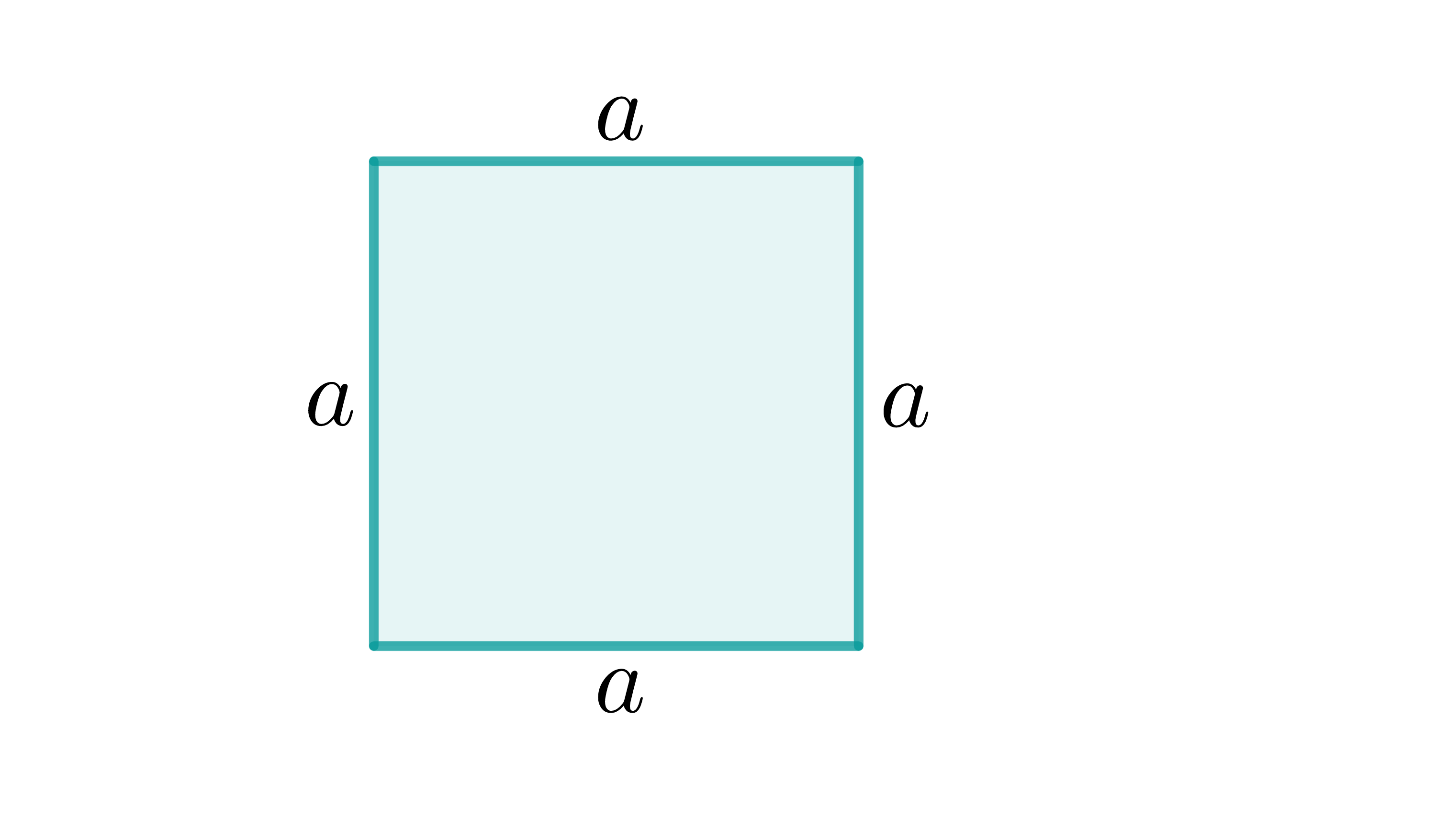
Rechteck
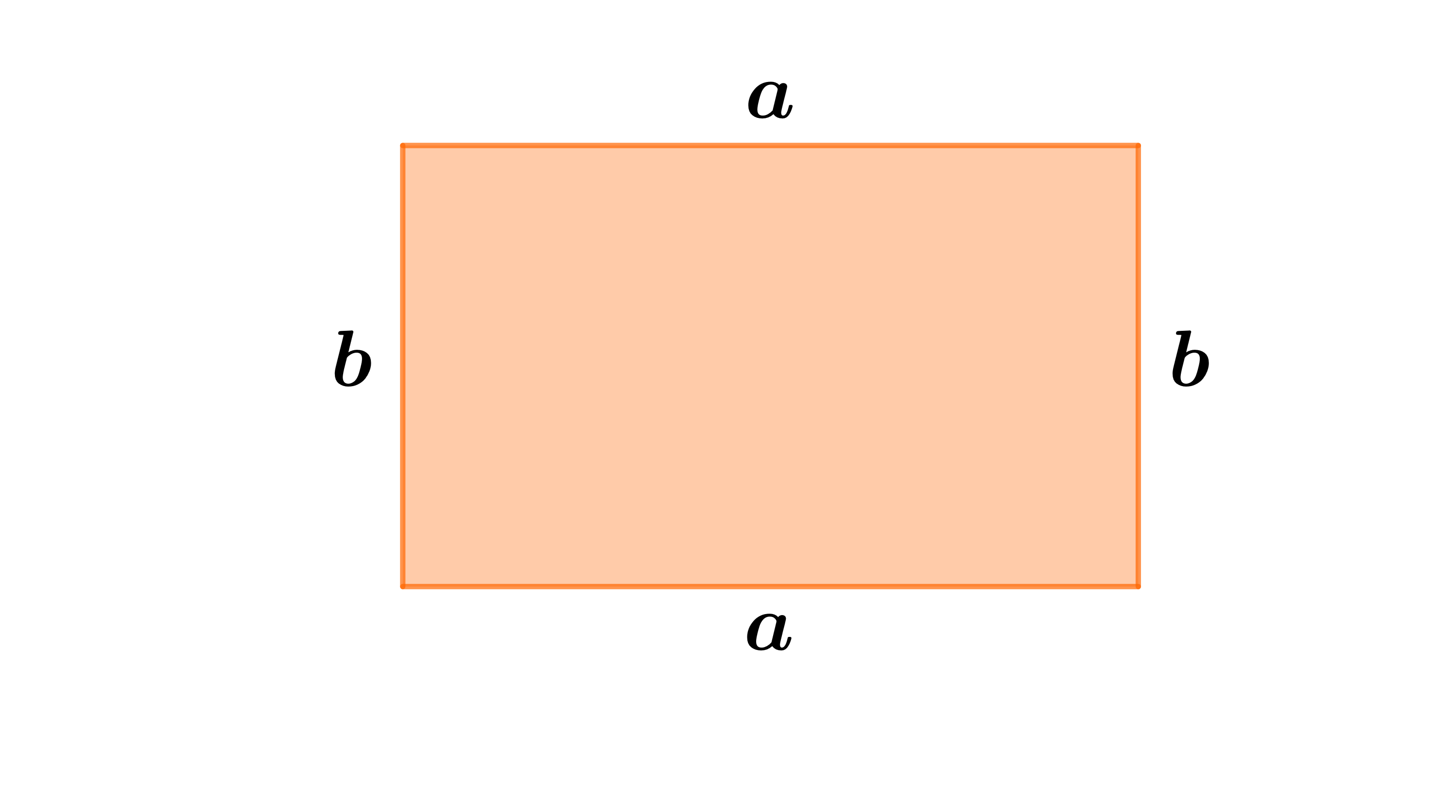
- 3
Gib an, wie du den Flächeninhalt folgender Formen berechnen kannst.
Quadrat
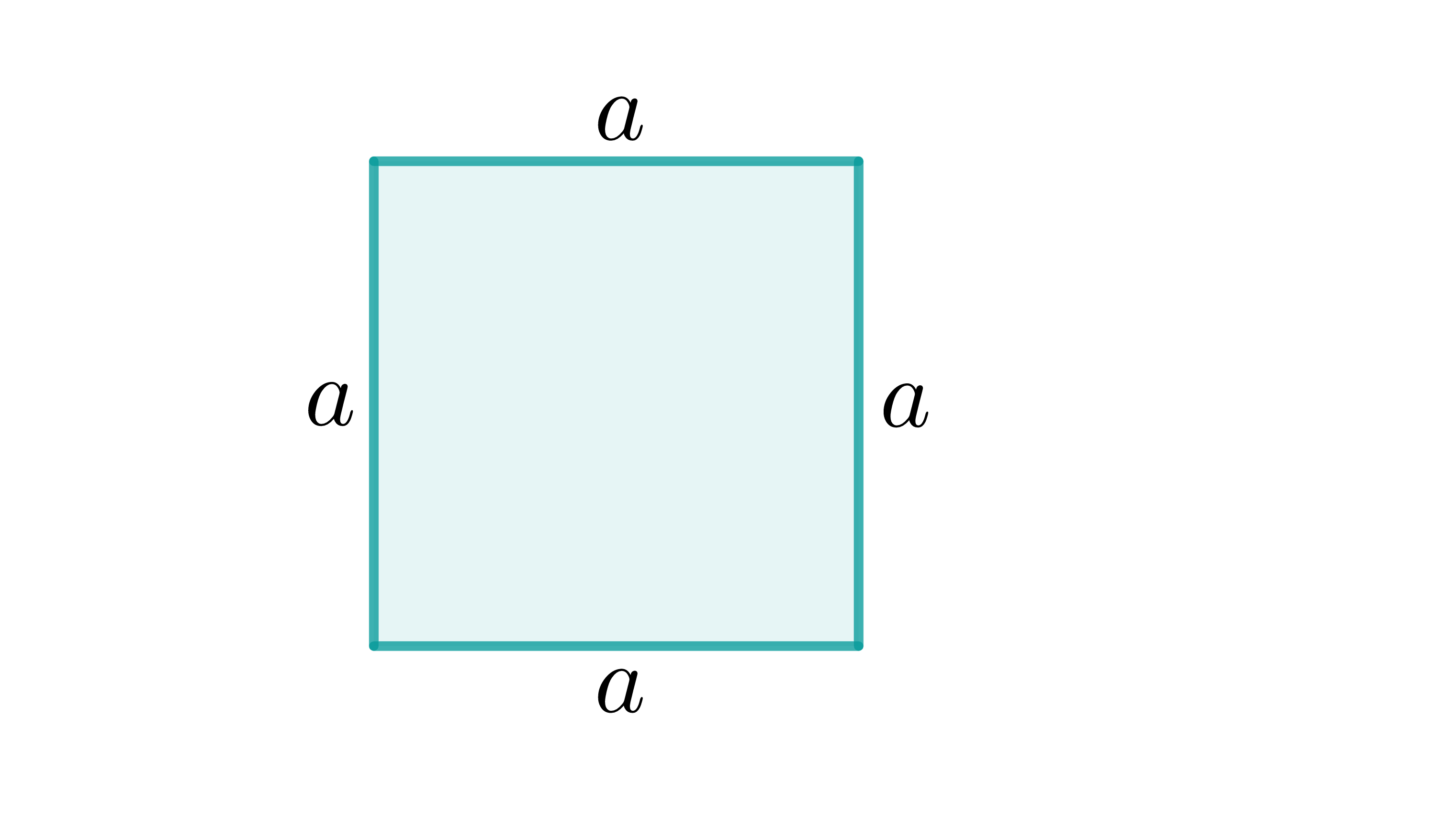
Rechteck

- 4
Berechne für ein Rechteck die fehlenden Größen:
Länge l
Breite b
Flächeninhalt A
Umfang U
a)
5 cm
7 dm
b)
30 cm
1,4 m
c)
120 m
6 ha
d)
80 cm
4 m²
- 5
Ein rechteckiger Garten der Länge 12m und der Breite 9,5m soll eingezäunt werden. Wie lang ist der Zaun, wenn für zwei Gartentore jeweils 2,7m ausgespart werden?
m - 6
Ein Fußballfeld ist 110 m lang und 75 m breit. Berechne die Fläche und den Umfang des Fußballfelds.
- 7
Manuelas Zimmer ist 4 m lang, 3,5 m breit und 2,5 m hoch.
Eine der beiden großen Wandflächen soll einen gelben Farbanstrich erhalten. Von einem Farbtopf mit der Aufschrift "Inhalt 2,5 l ausreichend für 20 - 25 " ist noch die Hälfte übrig.
Reicht die Menge für den Anstrich der Wand? Begründe deine Antwort durch Rechnung.
- 8
Durch Aneinanderlegen von 24 quadratischen Teppichfliesen soll eine lückenlose rechteckige Spielfläche gebildet werden. Jede Teppichfliese hat 0,5m Seitenlänge. Maria hat ein Rechteck mit 6 Fliesen an einer Längsseite und 4 Fliesen an einer Breitseite gelegt. Berechne den Umfang und den Flächeninhalt der Spielfläche. Gib alle weiteren Möglichkeiten an, aus allen 24 Fliesen eine rechteckige Spielfläche zu legen.
- 9
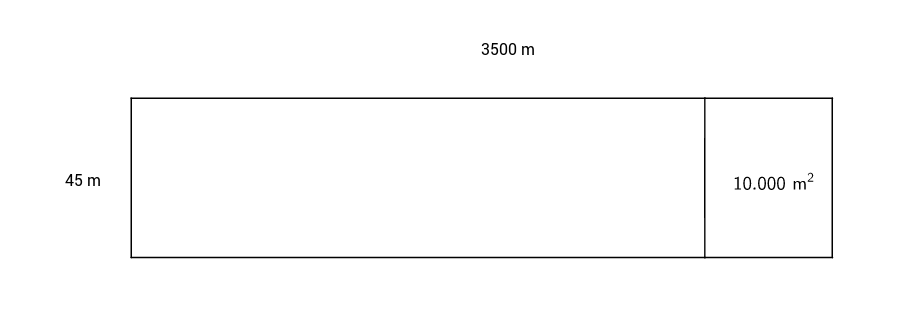
Eine Landebahn an einem internationalem Flughafen ist im fertigen Zustand insgesamt 45 m breit und 3 500 m lang. Allerdings muss der letzte Abschnitt der Landebahn welcher 10 000 groß ist noch gebaut werden.
Skizziere die Landebahn. Berechne anschließend den Umfang der gesamten Landebahn und den Flächeninhalt des fertigen Landebahn Abschnitts.
- 10
Wie lang muss ein Zaun sein, der ein quadratisches Grundstück der Fläche umgibt?
m - 11
Ein rechteckiges Grundstück ist 21m lang und hat einen Flächeninhalt von . Berechne die Breite und den Umfang des Grundstücks.
- 12
Aus einem Drahtstück wird ein Rechteck der Fläche gebogen, wobei eine Seite des Rechtecks 4 cm lang ist. Welche Länge hat der Draht?
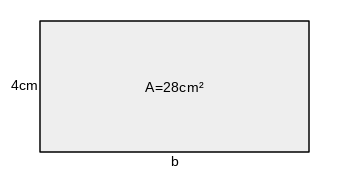 cm
cm - 13
Berechne x am Rechteck ABCD. (Die Zeichnung ist nicht maßstabgerecht.)
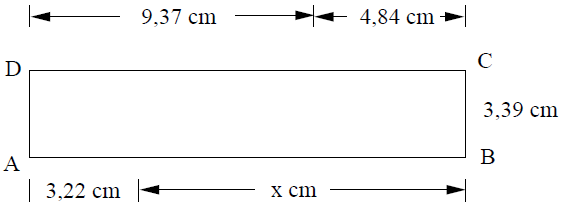 cm
cm - 14
Ein Rechteck hat den Umfang . Eine Seite ist länger als die benachbarte Seite. Berechne die Seitenlängen.
- 15
Verlängert man zwei gegenüberliegende Seiten eines Quadrats um jeweils 3 cm und verkürzt die anderen Seiten um jeweils 2 cm, so entsteht ein Rechteck, dessen Flächeninhalt um größer ist als der des Quadrats. Wie lang sind die Seiten des Quadrats?
cm - 16
Ein Quadrat hat den Flächeninhalt . Ein Rechteck, in dem eine Seite doppelt so lang wie die andere ist, hat den gleichen Umfang wie das Quadrat. Welchen Flächeninhalt hat das Rechteck?
cm² - 17
Ein Rechteck hat die Seitenlängen und . Wie groß ist die Fläche des Umkreises? Runde auf 3 Kommastellen.
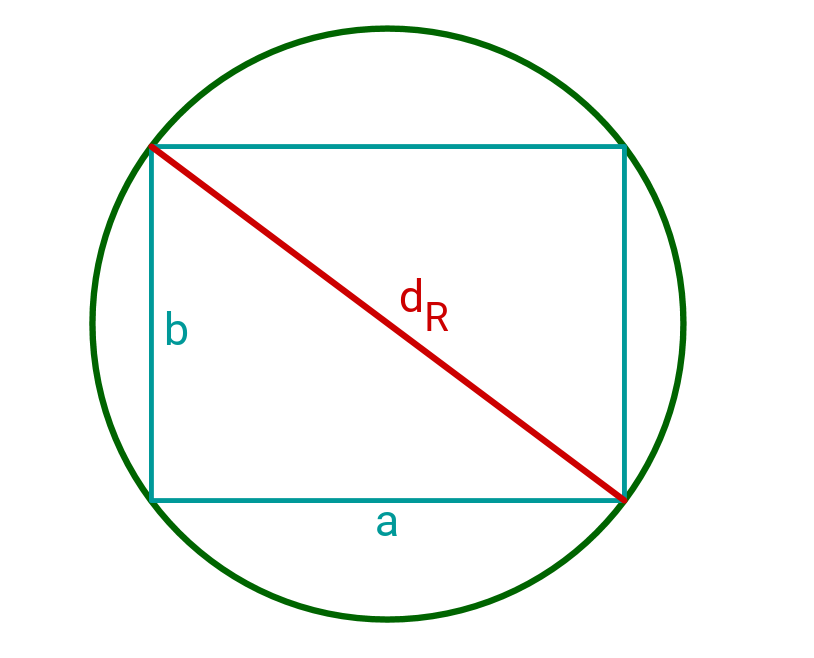 cm²
cm² - 18
Wie viele Quadrate zu je 2,5 cm Seitenlänge ergeben einen Quadratmeter?
- 19
Zeichne verschiedene Rechtecke mit einem Flächeninhalt von 12 Flächeneinheiten (FE).
- 20
Zeichne verschiedene Rechtecke mit einem Umfang von 16 Längeneinheiten (LE).
- 21
Ein quadratischer Teppich hat eine Seitenlänge von 3m. Berechne den Flächeninhalt.
m² - 22
Eine Fliese im Bad ist quadratisch und hat eine Fläche von . Berechne die Länge der Seiten.
cm - 23
Wie lang sind die fehlenden Seitenlängen der Rechtecke und Quadrate? Überlege
A = 20cm²
A = 42cm²
A = 36cm²
A = 64cm²
- 24
Die Nationalfahne der Schweiz zeigt ein weißes Kreuz auf rotem Grund. Für die vier kongruenten Arme des Kreuzes ist durch Beschluss der Schweizer Bundesversammlung aus dem Jahr 1889 festgelegt: Die Länge eines Arms ist um der Breite größer als (vergleiche Abbildung).
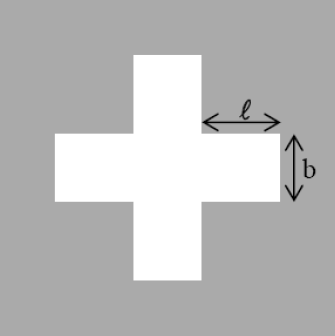
Wie lang ist ein Arm, wenn seine Breite beträgt?
cmStelle einen Term auf, der den Flächeninhalt des weißen Kreuzes in Abhängigkeit von der Breite b eines Arms beschreibt. Fasse den Term, in dem nur noch als Variable vorkommen soll, so weit wie möglich zusammen.
- 25
Eigenschaften eines Rechtecks
Welche Seiten eines Rechtecks sind gleich lang?
- 26
Wie viel Grad beträgt die Winkelsumme eines Rechtecks?
- 27
Auf einem unbebauten, rechteckigen Grundstück, das lang und breit ist, soll ein Spiel- und Sportplatz angelegt werden.
Das Gelände soll dazu rundherum mit einem Zaun umgeben werden.
Wie viele Zaun braucht man, wenn dabei an einer Stelle für das Eingangstor frei gelassen werden müssen?
mWas kostet das Einzäunen des Grundstücks, wenn die Stadtverwaltung für Zaun bezahlen muss, und das Tor kostet?
€
- 28
Ein rechteckiges Grundstück wird vermessen und die Länge auf und die Breite auf festgelegt.
Welchen Flächeninhalt besitzt das Grundstück?
m²Ein Käufer bietet für das Grundstück . Von welchem Preis pro Quadratmeter geht der Käufer aus? (auf Euro genau).
€/m²Der Käufer will auf dem Grundstück ein Hotel einrichten. Die örtlichen Bauvorschriften besagen, dass höchstens ein Drittel des Grundstücks bebaut werden darf. Welche Grundfläche hat das Hotel, wenn der Käufer das Höchstmaß dafür sogar um unterschreitet.
m²
- 29
Das ist ein Bild der Nationalflagge von England. Diese Fahne ist aus einem Tuch gefertigt worden, das lang und breit ist.
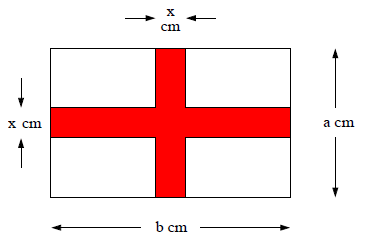
Zeichne die Figur für .
Berechne den Flächeninhalt eines der weißen Rechtecke im Inneren, wenn das Kreuz der Gesamtfläche einnimmt und die vier weißen Rechtecke kongruent sind.
m²
- 30
Miriam fällt ein besonderes Muster auf dem Boden einer Eingangshalle auf.
Sie erfährt, dass der Kreis einen Radius von zwei Metern hat.

Berechne den Flächeninhalt des blauen Quadrats.
m²Berechne den Flächeninhalt des orangenen Quadrats.
m²
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?