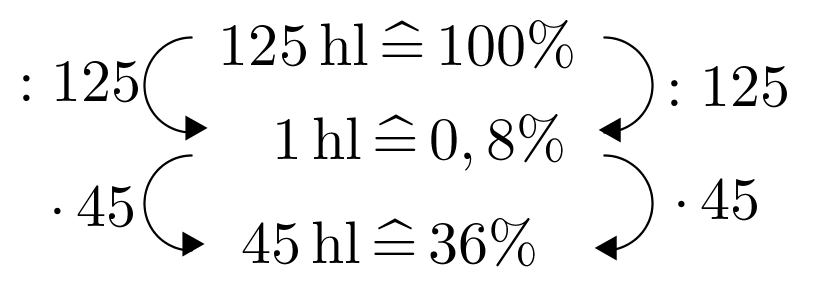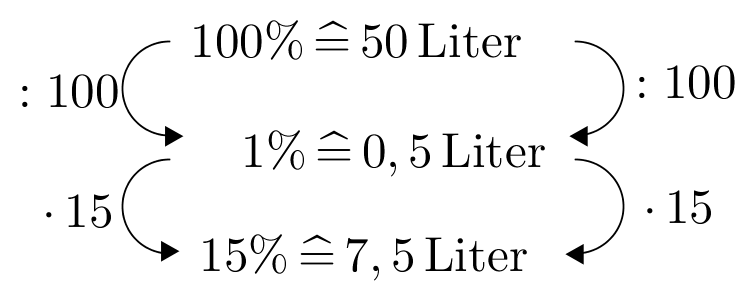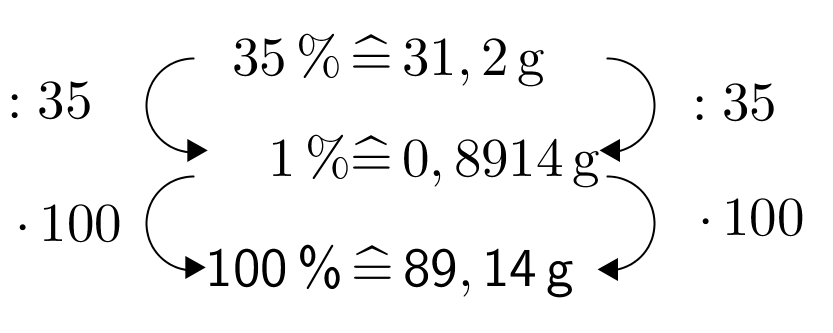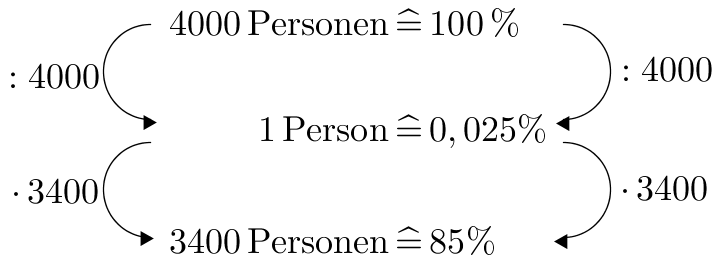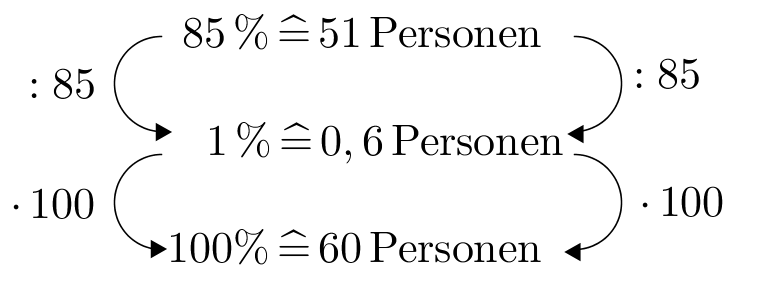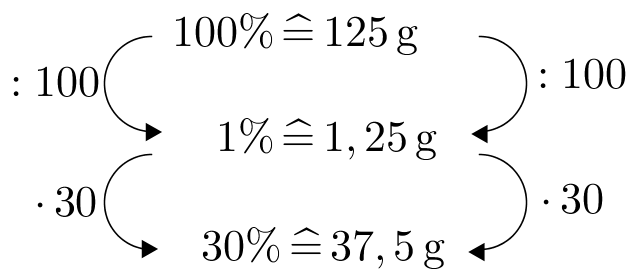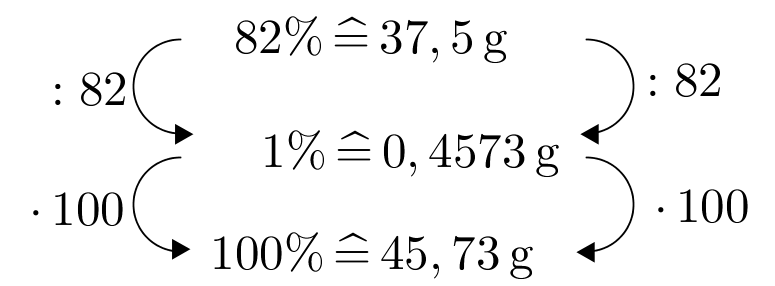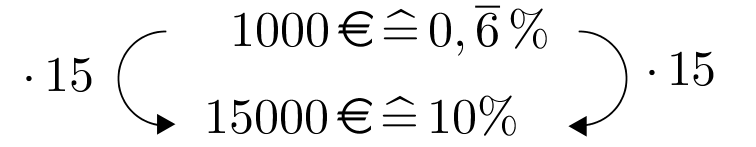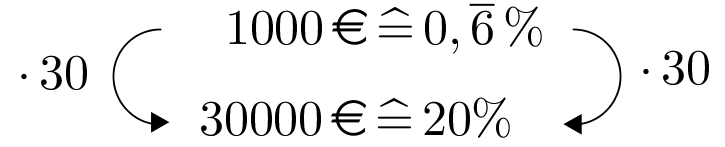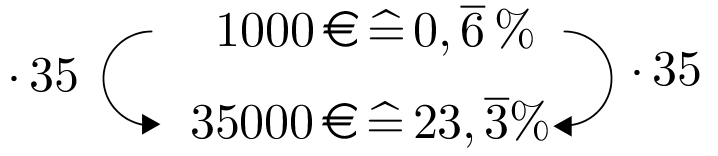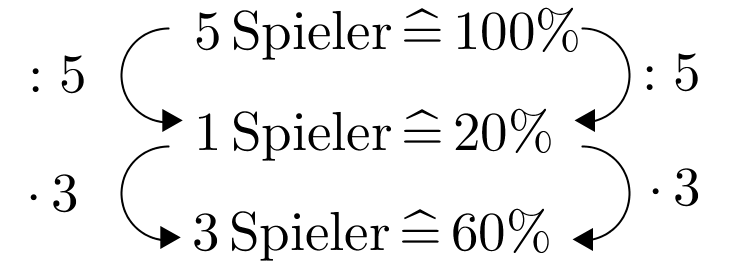Aufgaben zur Prozentrechnung
Übe das Rechnen mit Prozent mit diesen gemischten Aufgaben. Schaffst du sie alle?
- 1
Sommer Sale
Für ein Spiel sind nach Rabatt noch zu bezahlen.
Berechne den Preis, der das Spiel vor dem Rabatt gekostet hat.

- 2
Prozentwert
Berechne den Prozentwert und ordne die richtigen Antworten zu:
- 3
Grundwert
Berechne den Grundwert mittels Formel.
50% entsprechen 100 €.
30 % entsprechen 900 g.
125% entsprechen 500 €.
- 4
Recycling
Eine PET Flasche wiegt 30g. Davon sind 27g wieder verwertbar.

Wie viel Prozent der Flaschen sind wieder verwertbar?
%In einer Recyclingstelle befinden sich sehr viele PET Flaschen, die zusammen 150 kg wiegen. Wie viel kg wieder verwertbaren Materials befinden sich darunter?
kg
- 5
Lieblingsfilm
Die Klasse 8a wird nach ihrem Lieblingsfilm befragt.
40% von den 25 abgegebenen Stimmzetteln enthalten den Film "Friss oder Stirb".
Eva ist sich bei 9 Klassenkamerad*innen sicher, dass sie diesen Film gewählt haben.
Wie viele Schüler*innen haben für den Film gestimmt, von denen Eva das nicht weiß?

- 6
Tennisverein
Der Tennisverein in Wolkenheim hat Mitglieder.
davon sind Erwachsene, der restliche Anteil Jugendliche.
Dem Verein treten Erwachsene und Jugendliche neu bei.

Wie viele Jugendliche sind nach den Neueintritten im Verein?
Wie viel Prozent Erwachsene sind danach im Verein?
Runde den Prozentsatz auf eine Stelle nach dem Komma.
%
- 7
Festival
Im Vorverkauf für ein Open-Air-Festival mit
20 000 Plätzen wurden 12 000 Eintrittskarten verkauft.
Während der Veranstaltung war das Festival zu 90% ausgelastet.
Eine Karte im Vorverkauf kostete 20 €. Direkt vor Ort kostete eine Karte 25 €.
Berechne die Gesamteinnahmen.
 €
€ - 8
Wasser und Eis
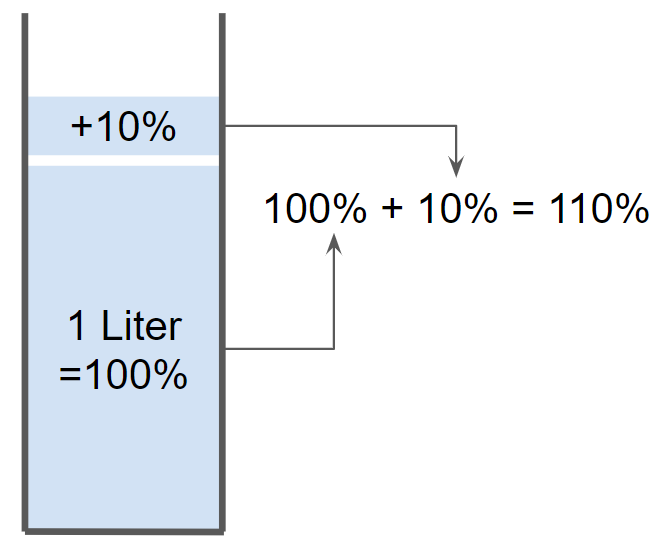
Wasser vergrößert sein Volumen beim Gefrieren um 10%.

Berechne das Volumen des Eises, das dann aus 1 Liter Wasser entstanden ist.
lWie viele Liter Wasser entstehen, wenn Liter Eis schmelzen?
lIm Wasserglas rechts sind 6 Eiswürfel. Jeder Eiswürfel hat ein Volumen von 60 ml.
In das Glas passen 330 ml Flüssigkeit hinein.
Wieviel Wasser entsteht beim Schmelzen der 6 Eiswürfel? Runde das Ergebnis auf ganze ml.
Läuft das Glas beim Schmelzen über?
 ml
ml
- 9
Welche beiden Aufgaben haben das gleiche Ergebnis? Klicke die beiden Aufgaben an.
- 10
Eine Klasse hat Kinder. Davon sind im Sportverein.
Welche Rechnung ist hier richtig?
- 11
Ein Fluss fließt durch ein Wüstenland, das zwei Beduinengruppen bewohnen. Die eine Gruppe zweigt 80 von den 125 Hektolitern, die der Fluss pro Stunde mit sich bringt, für ihre Felder ab. Wie viel Prozent der Wassermenge des Flusses kommt dann noch bei der anderen Beduinengruppe an, die bergab des Flusses lebt?
- 12
Laura findet eine Brieftasche mit 1125 € Inhalt. Der glückliche Besitzer der Brieftasche zahlt den gesetzlichen Finderlohn von 5% für die ersten 500 € und 3% für den Rest.
Wie hoch ist der Finderlohn?
€ - 13
Vor der Fahrt von Berlin nach München hat Werner sein Auto vollgetankt. Der Tank fasst 50 Liter Benzin. Nach einer Stunde Fahrt zeigt die Tanknadel an, dass 15% verbraucht wurden. Wie viele Liter Benzin werden in 3 Stunden verbraucht?
Liter - 14
Wie viel Zucker darfst du am Tag essen?

Schätze die empfohlene Tagesmenge ab.
Berechne die empfohlene Tagesmenge mit dem Dreisatz.
g
- 15
In einer Umfrage sagen 3400 von 4000 Leuten, dass sie Greenpeace toll finden. Inga Schiert macht eine eigene Umfrage. In dieser finden 51 Leute Greenpeace toll. Wie viele Leute hat Inga wohl ungefähr befragt?
Leute - 16
Ein Holzspielzeug "Serlo" wiegt 5 kg, wovon 4,5 kg wieder verwertbar sind. In einer Recyclingstelle befinden sich sehr viele Serlos, die zusammen 750 kg wiegen. Wie viel kg wieder verwertbaren Materials befinden sich darunter?
kg - 17
Butter hat einen Fettgehalt von 82%, Creme Fraiche enthält 30% Fett.
Wie viel Gramm Butter enthält die gleiche Menge Fett wie ein Becher mit 125 g Creme Fraiche?
g Butter - 18
Der Grundpreis eines Wagens beträgt 27500 €. Die Sonderausstattung erhöht den Preis um 1000 €. Wegen Barzahlung erhält der Käufer 12% Rabatt.
Wie viel Prozent vom Grundpreis sind tatsächlich gezahlt worden?
% - 19
1 € geschenkt!


Zwei Angebote werben beim Kauf eines Getränkekastens mit einem Preisnachlass von 1 €. Welches Angebot ist prozentual günstiger?
- 20
In einem Baumarkt werden zwei Artikel zu Einzelpreisen von 65 € und 47,50 € angeboten. Beide Artikel zusammen bekommt man für 102 €.
Wie hoch sind die Rabatte in Prozent, wenn für den ersten Artikel der Rabatt 2,5-mal so hoch ist, wie der Rabatt für den zweiten?
- 21
Die Tabelle zeigt, wie viele Euro-Geldscheine am 31. Mai 2007 in Umlauf waren. Beispielsweise befanden sich von den 200 Euro-Scheinen 153 Millionen Stück in Umlauf.
Wert
Anzahl der Scheine in Millionen
500 EUR
429
200 EUR
153
100 EUR
1116
50 EUR
3983
20 EUR
2244
10 EUR
1804
5 EUR
1325
Wie hoch war der Gesamtwert aller 50 Euro-Scheine?
Ungefähr wie viel Prozent aller in Umlauf befindlichen Scheine waren 20 Euro- Scheine?
Die notwendigen Rechnungen brauchen nicht exakt ausgeführt zu werden, es genügt jeweils ein Überschlag.
Der Lösungsweg muss nachvollziehbar sein.
- 22
Eine Person steigt eine Treppe mit 50 Stufen empor. Jede Stufe ist 16 cm hoch und 35 cm tief. Wie viel Prozent Steigung überwindet die Person?
Hinweis: Steigung ist der Quotient aus Höhendifferenz und Horizontaldifferenz.
% - 23
In einer Sportgruppe fahren der Schüler Ski und der Schüler Snowboard. Ein Viertel der Schüler fährt weder Ski noch Snowboard. Schüler der Gruppe fahren Ski und Snowboard.
Stelle die Anteile mittels einer Vierfeldertafel dar.
Ermittle, wie viele Schüler insgesamt in der Sportgruppe sind.
- 24
Die Fußballspieler einer Mannschaft der 1. Liga müssen wegen ihren begangenen Unsportlichkeiten Strafen in die Mannschaftskasse zahlen. A. Mateur muss bezahlen, B. Trüger , C. Rung , D. M. Lich und E. Goist .
Wieviel Prozent des Gesamtbetrags der Mannschaftskasse muss jeder einzelne Fußballer zahlen?
Wie viele der 5 Fußballer müssen jeweils mindestens des Gesamtbetrags zahlen? Wie viel Prozent der Spieler sind das?
%
- 25
Franz hat in seinem Sommerurlaub viel fotografiert. Er hat insgesamt 50 Fotos geschossen, von denen jedes Speicherplatz benötigt. Seine SD-Karte hat eine Speicherkapazität von .
Wie viel Prozent des Speichers ist nach dem Urlaub noch frei?
%Wie viele Bilder kann er auf seinem nächsten Ausflug machen, wenn die neuen Bilder doppelt so viel Speicher benötigen und schon des Speichers belegt sind?
Fotos
- 26
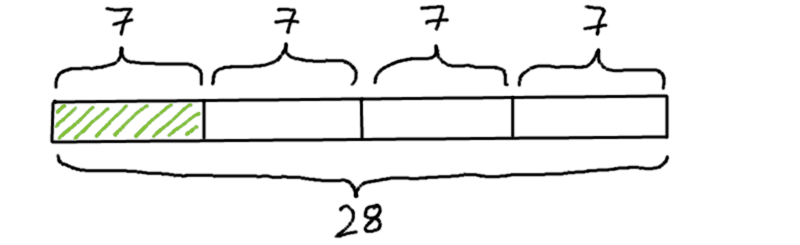
Aufwärmübung zur Prozentrechnung. Rechne im Kopf:
von
von
von
- 27
In einer Klasse singen 12 Schüler im Chor, das sind ca. 39 % der Schüler dieser Klasse.
Berechne, wie viele Schüler in dieser Klasse sind. Runde auf ganze Schüler.
SchülerDie Polizei stellt bei einer Überprüfung von 400 Fahrrädern fest, dass 35 % davon nicht verkehrssicher waren. Von diesen wurden wegen defekter Bremsen beanstandet. Wie viele Räder waren das?
Räder sind defekt.Wie viel % von 2400 kg sind 72 kg?
%
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?