Lagebeziehung zwischen Kugeln und Geraden

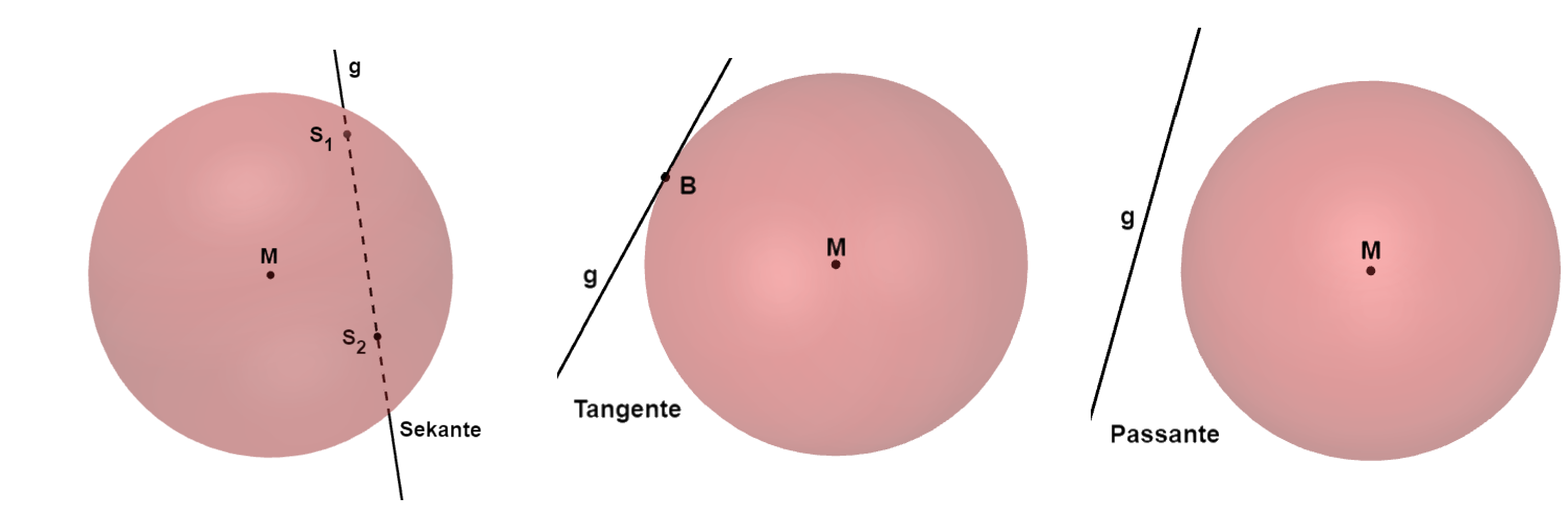
Es wird die Lage einer Geraden $g$ bezüglich einer Kugel $K$ untersucht.

Dabei treten drei Fälle auf:

die Gerade schneidet die Kugel in zwei Punkten, d.h. die Gerade ist eine Sekante (linkes Bild)
die Gerade berührt die Kugel in genau einem Punkt, d.h. die Gerade ist eine Tangente (mittleres Bild)
die Gerade schneidet die Kugel nicht, d.h. die Gerade ist eine Passante (rechtes Bild)

Allgemeines Vorgehen

Gegeben sind eine Kugel $K$ mit dem Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ , dem Radius $r$ und eine Gerade $g$ .

$K : {(\vec{x} - (\begin{array}{c} m_{1} \\ m_{2} \\ m_{3} \end{array}))}^{2} = r^{2}$ ; Gerade $g : \vec{X} = \vec{A} + t \cdot \vec{u}$

Zur Lageüberprüfung wird die Geradengleichung von $g$ für den Vektor $\vec{x}$ in die Kugelgleichung $K$ eingesetzt.

$K : {((\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) + t \cdot (\begin{array}{c} u_{1} \\ u_{2} \\ u_{3} \end{array}) - (\begin{array}{c} m_{1} \\ m_{2} \\ m_{3} \end{array}))}^{2}$	$=$	$r^{2}$
	↓	Die linke Seite der Gleichung wird vereinfacht.
${(\begin{array}{c} a_{1} - m_{1} + t \cdot u_{1} \\ a_{2} - m_{2} + t \cdot u_{2} \\ a_{3} - m_{3} + t \cdot u_{3} \end{array})}^{2}$	$=$	$r^{2}$
	↓	Berechne das Skalarprodukt.
$(a_{1} - m_{1} + t \cdot u_{1})^{2} + (a_{2} - m_{2} + t \cdot u_{2})^{2} + (a_{3} - m_{3} + t \cdot u_{3})^{2}$	$=$	$r^{2}$
	↓	Rechne die Quadrate aus und fasse zusammen. Vergiss nicht die binomische Formel anzuwenden.

Du hast eine quadratische Gleichung mit der Unbekannten $t$ erhalten. Diese quadratische Gleichung kannst du mit der Mitternachtsformel (abc-Formel) oder pq-Formel lösen.

Je nach Anzahl der erhaltenen Lösungen tritt einer der oben genannten $3$ Fälle ein:

gibt es zwei Lösungen, dann ist die Gerade eine Sekante
gibt es genau eine Lösung, dann ist die Gerade eine Tangente
gibt es keine Lösung, dann ist die Gerade eine Passante

Musterbeispiel

Gegeben ist eine Kugel $K$ mit dem Mittelpunkt $M (3 | 2 | 4)$ und dem Radius $r = \sqrt{10}$ .

Untersuche die Lage der Geraden $g : \vec{X} = (\begin{array}{c} 1 \\ 3 \\ 8 \end{array}) + t \cdot (\begin{array}{c} 5 \\ - 1 \\ - 3 \end{array})$ bezüglich der Kugel $K$ . Gib gegebenenfalls die Koordinaten aller Schnittpunkte an.

Lösung:

Stelle die Kugelgleichung auf.
	↓
$K : {(\vec{x} - (\begin{array}{c} 3 \\ 2 \\ 4 \end{array}))}^{2}$	$=$	$(\sqrt{10})^{2}$
	↓	vereinfache
$K : {(\vec{x} - (\begin{array}{c} 3 \\ 2 \\ 4 \end{array}))}^{2}$	$=$	$10$
	↓	Setze für $\vec{x}$ die Gleichung der Geraden $g$ ein.
${((\begin{array}{c} 1 \\ 3 \\ 8 \end{array}) + t \cdot (\begin{array}{c} 5 \\ - 1 \\ - 3 \end{array}) - (\begin{array}{c} 3 \\ 2 \\ 4 \end{array}))}^{2}$	$=$	$10$
	↓	Die linke Seite der Gleichung wird vereinfacht.
${(\begin{array}{c} - 2 + 5 \cdot t \\ 1 - t \\ 4 - 3 \cdot t \end{array})}^{2}$	$=$	$10$
	↓	Berechne auf der linken Seite das Skalarprodukt.
$(- 2 + 5 t)^{2} + (1 - t)^{2} + (4 - 3 t)^{2}$	$=$	$10$
	↓	Vergiss nicht die binomische Formel anzuwenden.
$4 - 20 t + 25 t^{2} + 1 - 2 t + t^{2} + 16 - 24 t + 9 t^{2}$	$=$	$10$
	↓	Fasse zusammen.
$35 t^{2} - 46 t + 21$	$=$	$10$	$- 10$
$35 t^{2} - 46 t + 11$	$=$	$0$

Du hast die quadratische Gleichung $35 t^{2} - 46 t + 11 = 0$ mit der Unbekannten $t$ erhalten. Diese Gleichung kannst du mit der Mitternachtsformel (abc-Formel) oder pq-Formel lösen. Hier erfolgt die Lösung mit der Mitternachtsformel.

Lies dazu die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein:

$a = 35$ , $b = - 46$ , $c = 11$

$t_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze $a = 35$ , $b = - 46$ und $c = 11$ ein.
	$=$	$\frac{- (- 46) \pm \sqrt{(- 46)^{2} - 4 \cdot 35 \cdot 11}}{2 \cdot 35}$
	↓	vereinfache
	$=$	$\frac{46 \pm \sqrt{2116 - 1540}}{70}$
	$=$	$\frac{46 \pm \sqrt{576}}{70}$
	$=$	$\frac{46 \pm 24}{70}$
$t_{1}$	$=$	$\frac{11}{35}$
$t_{2}$	$=$	$1$

Die quadratische Gleichung hat die Lösungsmenge $𝕃 = {\frac{11}{35}; 1}$ . Da es zwei Lösungen gibt, schneidet die Gerade $g$ die Kugel $K$ in zwei Punkten. Die Gerade $g$ ist eine Sekante.

Schnittpunkte berechnen

Setze die zwei gefundenen Parameter $t_{1}$ und $t_{2}$ in die Geradengleichung

$g : \vec{X} = (\begin{array}{c} 1 \\ 3 \\ 8 \end{array}) + t \cdot (\begin{array}{c} 5 \\ - 1 \\ - 3 \end{array})$ ein.

$t_{1} = \frac{11}{35}$

${\vec{X}}_{S_{1}} = (\begin{array}{c} 1 \\ 3 \\ 8 \end{array}) + \frac{11}{35} \cdot (\begin{array}{c} 5 \\ - 1 \\ - 3 \end{array}) = (\begin{array}{c} 1 + \frac{55}{35} \\ 3 - \frac{11}{35} \\ 8 - \frac{33}{35} \end{array}) = (\begin{array}{c} \frac{90}{35} \\ \frac{94}{35} \\ \frac{247}{35} \end{array})$

$t_{2} = 1$

${\vec{X}}_{S_{2}} = (\begin{array}{c} 1 \\ 3 \\ 8 \end{array}) + 1 \cdot (\begin{array}{c} 5 \\ - 1 \\ - 3 \end{array}) = (\begin{array}{c} 6 \\ 2 \\ 5 \end{array})$

Antwort: Die beiden Schnittpunkte haben die Koordinaten $S_{1} (\frac{90}{35} | \frac{94}{35} | \frac{247}{35})$ und $S_{2} (6 | 2 | 5)$ .

Übungsaufgaben

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?