Pflichtteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben zur Abiturprüfung eA 2023, Pflichtteil. Zum Download hier.

Aufgabe 1

Gegeben ist die in $ℝ$ definierte Funktion f mit $f (x) = - x^{2} + 2 a x$ mit $a > 1$ .

Die Nullstellen von $f$ sind $0$ und $2 a$ .

Zeigen Sie, dass das Flächenstück, das der Graph von $f$ mit der $x$ -Achse einschließt, den Inhalt $\frac{4}{3} a^{3}$ hat. (2 BE)

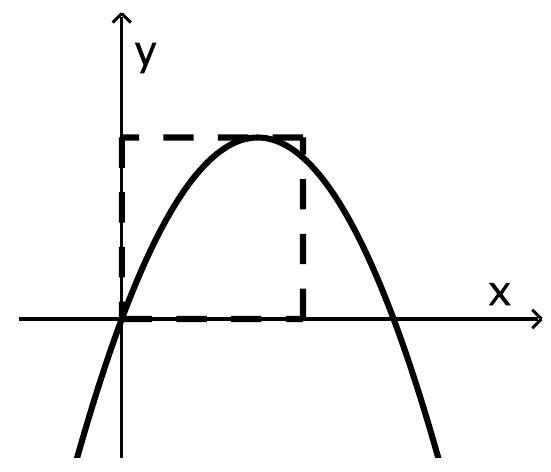
Der Hochpunkt ( $a | a^{2}$ ) des Graphen von $f$ liegt auf einer Seite eines Quadrats. Zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung). Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von $f$ mit der $x$ -Achse einschließt, überein.
Bestimmen Sie den Wert von $a$ . (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Flächeninhalt Quadrat:
Am Hochpunkt mit $x = a$ beträgt der Funktionswert $f (x) = a^{2}$ .
$\to$ Das Quadrat hat eine Seitenlänge von $a^{2}$ .
$A_{Q u a d r a t} = a^{2} \cdot a^{2} = a^{4}$
Flächeninhalt des Flächenstücks zwischen Graph und x-Achse:
Der Flächeninhalt wurde in a) bestimmt und beträgt
$A_{F l \ddot{a} c h e n s t \ddot{u} c k} = \frac{4}{3} a^{3}$
Gleichsetzen der Flächeninhalte:
Wenn beide Flächeninhalte gleich sind, gilt:
↓
$A_{Q u a d r a t}$ $=$ $A_{F l \ddot{a} c h e n s t \ddot{u} c k}$
↓
Einsetzen der Terme für die Flächeninhalte
$a^{4}$ $=$ $\frac{4}{3} a^{3}$ $: (a^{3})$
↓
Da $a > 1$ gilt, kann durch $a^{3}$ geteilt werden.
$a^{}$ $=$ $\frac{4}{3}$
$\to$ Bei einem Wert von $a = \frac{4}{3}$ sind die Flächeninhalte gleich groß.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme den Flächeninhalt des beschriebenen Quadrats.
Den Flächeninhalt zwischen dem Graphen von $f$ und der x-Achse hast du bereits in Teil a) bestimmt.
Setze beide Terme gleich und bestimme $a$ .

Aufgabe 2

Gegeben ist die auf $ℝ$ definierte Funktion $f$ mit $f (x) = 2 e^{x} - \frac{4}{e^{x}} = 2 e^{x} - 4 e^{- x}$ .

Berechnen Sie die Nullstelle von $f$ . (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle berechnen
Berechnung der Nullstelle
Der Funktionswert $f (x)$ wird gleich $0$ gesetzt.
↓
$f (x)$ $=$ $0$
$2 e^{x} - \frac{4}{e^{x}}$ $=$ $0$ $\cdot e^{x}$
$2 e^{2 x} - 4$ $=$ $0$ $+ 4$
$2 e^{2 x}$ $=$ $4$ $: 2$
$e^{2 x}$ $=$ $2$ $\ln ()$
$2 x$ $=$ $\ln (2)$ $: 2$
$x$ $=$ $\frac{1}{2} \ln (2)$
$\to$ Die Nullstelle von $f (x)$ liegt bei $x = \frac{1}{2} \ln (2)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
An der Nullstelle beträgt der Funktionswert $f (x) = 0$ .
Setze den Funktionsterm $2 e^{x} - \frac{4}{e^{x}} = 0$ .
Bestimme x.

Bestimmen Sie eine Gleichung der Tangente an den Graphen von $f$ im Schnittpunkt mit der $y$ -Achse. (3 BE)

3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 3
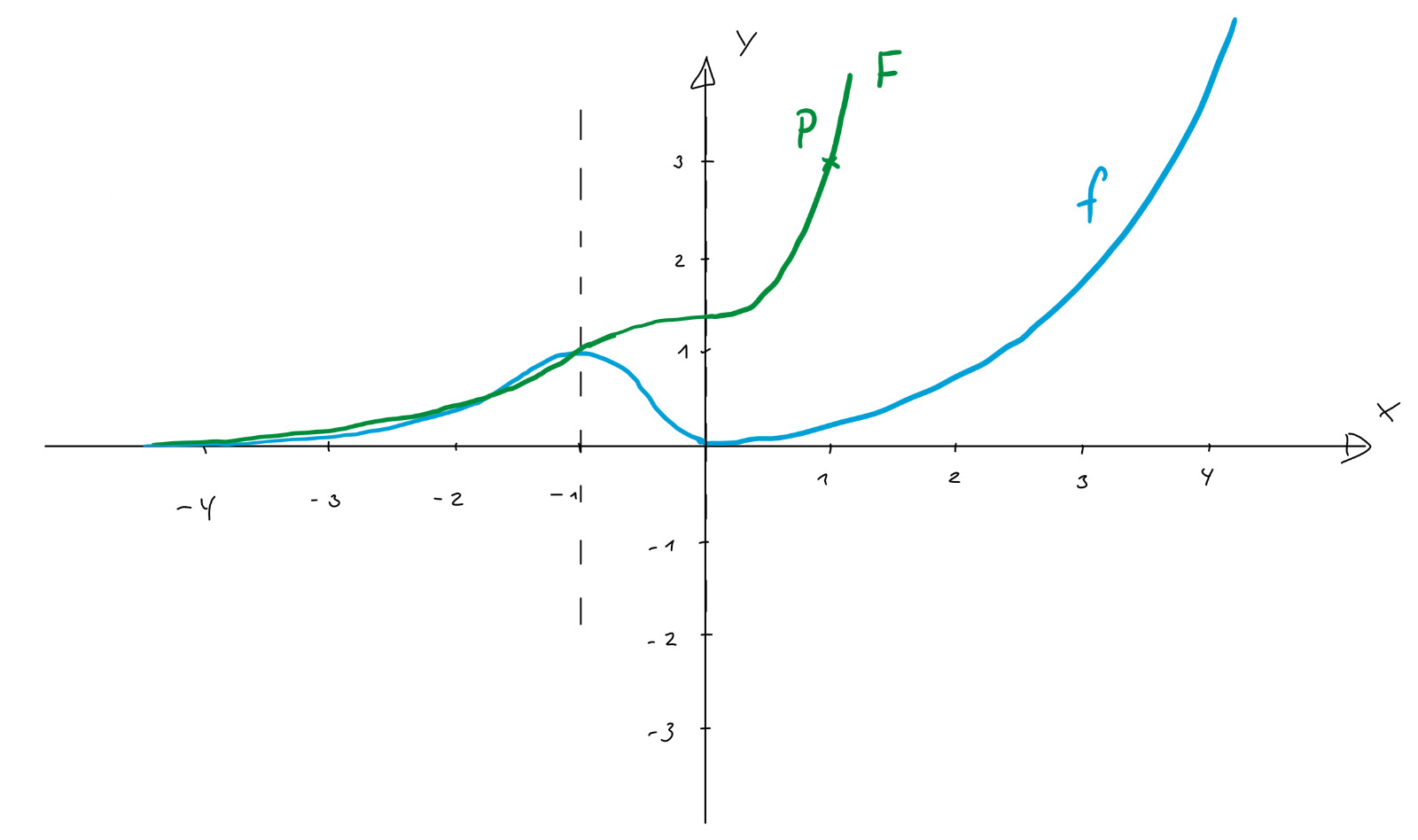
Die Abbildung zeigt den Punkt $P$ und den Graphen der in $ℝ$ definierten Funktion $f$ . Der Graph von $f$ hat die einzigen Extrempunkte $(- 1 | 1)$ und $(0 | 0)$ .
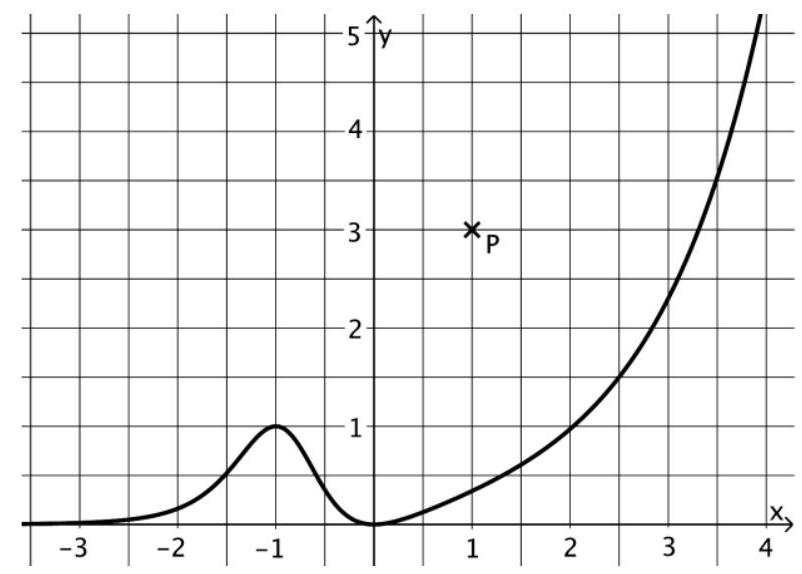
1. Gegeben ist die Funktion $g$ mit $g (x) = - f (x - 3)$ .
  Geben Sie die Koordinaten des Tiefpunkts des Graphen von $g$ an. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen verschieben
  Koordinaten des Punktes
  Der Graph der Funktion erfährt zwei Abbildungen:
  Spiegelung an der x-Achse. Der Hochpunkt wird zu einem Tiefpunkt $(- 1 | - 1)$
  Verschiebung nach rechts. Der Punkt ist $(2 | - 1)$
  Skizze (Graph ist nur qualitativ gleich wie in der Aufgabe)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Hochpunkt des Graphen wird der gesuchte Tiefpunkt.
  Bestimme die Koordinaten des Punktes $(1 | 1)$ , wenn der Graph durch die Vorschrift $g (x) = - f (x)$ an der x-Achse gespiegelt wird.
  Bestimme die Koordinaten, wenn nun zusätzlich eine Verschiebung um 3 LE nach rechts stattfindet.
2. Der Graph einer Stammfunktion von $f$ verläuft durch $P$ .
  Skizzieren Sie diesen Graphen in der Abbildung. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
  Anfertigen der Skizze
  Es ist zu beachten, dass
  der Hochpunkt von $f$ zu einem Wendepunkt von $F$ wird
  der Tiefpunkt (und gleichzeitig Nullstelle) von $f$ zu einem Sattelpunkt von $F$ wird
  $F$ durch $(3 | 1)$ verläuft und stets oberhalb der x-Achse bleibt
  Skizze der Stammfunktion
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Stammfunktion hat die Eigenschaft, dass ihre Steigung durch $f$ gegeben ist.
  Bestimme die Lage möglicher Extrempunkte der Stammfunktion.
  Bestimme die Lage möglicher Wendepunkte der Stammfunktion.
  Skizziere einen Graphen der durch diese Punkte und $P$ verläuft.

Aufgabe 4

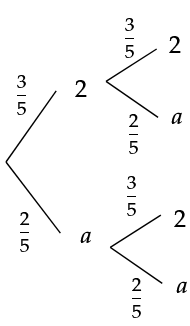
In einem Behälter befinden sich fünf Kugeln, auf denen jeweils eine Zahl steht. Auf drei der Kugeln steht die Zahl 2, auf zwei der Kugeln die Zahl $a$ mit $a \neq 2$ . Zweimal nacheinander wird eine Kugel zufällig entnommen und wieder zurückgelegt.

Geben Sie im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term $2 \cdot \frac{3}{5} \cdot \frac{2}{5}$ berechnet werden kann. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Baumdiagramm als Hilfe
Das Zufallsexperiment ist ein Laplace-Experiment.
Die Wahrscheinlichkeiten sind damit
$P (a) = \frac{2}{5}$
$P (2) = \frac{3}{5}$
Baumdiagramm
Ereignis
Das gesuchte Ereignis mit der Wahrscheinlichkeit $2 \cdot \frac{3}{5} \cdot \frac{2}{5}$ ist:
"Es wird eine $2$ und ein $a$ gezogen."
oder
"Auf beiden Kugeln stehen unterschiedliche Zahlen."
Da zwei Pfade zu dieser Beschreibung passen, gibt es den Vorfaktor $2 \cdot \frac{3}{5} \cdot \frac{2}{5}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Skizziere zur Hilfe ein Baumdiagramm, um die Wahrscheinlichkeiten $\frac{3}{5}$ und $\frac{2}{5}$ zuordnen zu können.
Bestimme ein Ereignis, welches genau zwei Pfade mit der Wahrscheinlichkeit $\frac{3}{5} \cdot \frac{2}{5}$ beinhaltet.

Die Zufallsgröße $X$ gibt die Summe der Zahlen an, die auf den beiden entnommenen Kugeln stehen. Der Erwartungswert von $X$ ist 8.

Bestimmen Sie den Wert von $a$ . (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert

Wahrscheinlichkeiten $P (X = k)$

Die Zufallsvariable $X$ kann folgende Werte annehmen:

$4$ falls zweimal die $2$ gezogen wird
$a + 2$ falls unterschiedliche Zahlen gezogen werden
$2 a$ falls zweimal die andere Zahl $a$ gezogen wird.

Die Wahrscheinlichkeiten ergeben sich mithilfe des Baumdiagramms (siehe Lösung a):

$X = k$	$4$	$2 + a$	$2 a$
$P (X = k)$	$\frac{9}{25}$	$\frac{12}{25}$	$\frac{4}{25}$

Aufstellen des Erwartungswertes

Erwartungswert ist die Summe der Werte, die $X$ annehmen kann, mal deren Wahrscheinlichkeit
	↓
$E [X]$	$=$	$4 \cdot \frac{9}{25} + (2 + a) \cdot \frac{12}{25} + 2 a \cdot \frac{4}{25}$
	↓	Klammer ausmultiplizieren
	$=$	$\frac{36}{25} + \frac{24}{25} + a \cdot \frac{12}{25} + a \cdot \frac{8}{25}$
	$=$	$\frac{60}{25} + a \cdot \frac{20}{25}$
	↓	Erwartungswert ist laut Aufgabe gleich $8$ .
$8$	$=$	$\frac{60}{25} + a \cdot \frac{20}{25}$	$- \frac{60}{25}$
$\frac{28}{5}$	$=$	$a \cdot \frac{4}{5}$	$\cdot 5$
$28$	$=$	$4 a$	$: 4$
$7$	$=$	$a$

$a$ hat den Wert $7$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

5
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 5
Gegeben ist die Gerade $g : \vec{x} = (\begin{array}{l} 0 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$ mit $s \in ℝ$ .
1. Zeigen Sie, dass $g$ in der Ebene mit der Gleichung $x + y + z = 2$ liegt. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
  Gerade in Ebenengleichung einsetzen
  Die Geradengleichung ist:
  $(\begin{array}{c} x \\ y \\ z \end{array}) = (\begin{array}{l} 0 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$
  $Zeilenweise liest man die Koordinaten aus \Rightarrow \begin{array}{l} x = s \\ y = 1 \\ z = 1 - s \end{array}$
  $2$ $=$ $x + y + z$
  ↓
  Setze die Gerade koordinatenweise in die Ebenengleichung ein
  $2$ $=$ $s + 1 + (1 - s)$
  ↓
  Vereinfache
  $=$ $2$
  Da die Gleichung erfüllt ist, liegt die Gerade $g$ in der Ebene $E$ .
  Man schreibt auch $g \subset E$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $g$ koordinatenweise in die Ebenengleichung ein.
  Überprüfe, ob die Gleichung erfüllt ist.
2. Gegeben ist außerdem die Schar der Geraden $h_{a} : \vec{x} = (\begin{array}{l} 0 \\ 0 \\ 1 \end{array}) + t \cdot (\begin{array}{l} 1 \\ a \\ 0 \end{array})$ mit $t \in ℝ$ und $a \in ℝ$ .
  Weisen Sie nach, dass $g$ und $h_{a}$ für jeden Wert von $a$ windschief sind. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
  Untersuchen der Richtungsvektoren
  Die Richtungsvektoren sind $(\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$ und $(\begin{array}{l} 1 \\ a \\ 0 \end{array})$ .
  Es gibt keine Zahl $k \in ℝ$ , sodass sie gleich sind: $(\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) \neq k \cdot (\begin{array}{l} 1 \\ a \\ 0 \end{array})$
  Die Vektoren sind linear unabhängig, die Geraden müssen entweder windschief sein oder sich schneiden.
  Gleichsetzen der Geradengleichungen
  Gleichsetzen
  ↓
  $(\begin{array}{l} 0 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$ $=$ $(\begin{array}{l} 0 \\ 0 \\ 1 \end{array}) + t \cdot (\begin{array}{l} 1 \\ a \\ 0 \end{array})$
  ↓
  Bringe alle Stützvektoren nach links und alle Richtungsvektoren nach rechts.
  $(\begin{array}{l} 0 \\ 1 \\ 0 \end{array})$ $=$ $t \cdot (\begin{array}{l} 1 \\ a \\ 0 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array})$
  Das ist ein lineares Gleichungssystem mit zwei Unbekannten.
  Dieses LGS besitzt keine Lösung.
  Es gibt verschiedene Methoden, die Lösung zu bestimmen. Betrachtet man die Zeilen etwas genauer, zeigt sich:
  $3. Zeile: 0 = t \cdot 0 + s \Rightarrow s = 0$
  Wenn $s = 0$ folgt aus der $1.$ Gleichung:
  $0 = t + \underset{= s}{\underset{⏟}{0}} \cdot (- 1) \Rightarrow t = 0$
  Für $t = 0$ und $s = 0$ folgt aber aus der 2. Gleichung: $1 \neq 0 \cdot a$
  Für keinen Wert von $a$ besitzt das LGS eine Lösung. Die Geraden haben keinen Schnittpunkt und sind damit windschief.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Windschiefe Geraden sind nicht parallel oder identisch.
  Überprüfe, ob die Richtungsvektoren Vielfache voneinander sind, um die Fälle parallel und/oder identisch auszuschließen.
  Windschiefe Geraden schneiden sich nicht.
  Setze die Geradengleichungen gleich und löse das LGS, um zu überprüfen, ob es einen Schnittpunkt gibt.
6
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 6
Betrachtet wird ein Dreieck $A B C$ mit $A (0 | 0 | 0)$ und $B (3 | 5 | - 4)$ . Das Dreieck hat die folgenden Eigenschaften:
Das Dreieck ist sowohl gleichschenklig als auch rechtwinklig.
$A B$ ist eine Kathete des Dreiecks.
Die zweite Kathete des Dreiecks liegt in der $x z$ -Ebene.
Ermitteln Sie die Koordinaten eines Punkts, der für $C$ infrage kommt. (5 BE)
1. Gleichung - rechtwinklige Katheten
Die Katheten $\vec{A C}, \vec{A B}$ stehen senkrecht aufeinander. Es gilt:
$0$ $=$ $(\begin{array}{c} x \\ 0 \\ z \end{array}) \cdot (\begin{array}{c} 3 \\ 5 \\ - 4 \end{array})$
↓
Skalarprodukt ausrechnen
$0$ $=$ $3 x - 4 z$
Aus dieser Gleichung lässt sich $x = \frac{4}{3} z$ bestimmen. Das wird später gebraucht.
2. Gleichung - Länge der Katheten
Die Katheten $\vec{A C}, \vec{A B}$ sind gleich lang laut der Aufgabenstellung, denn sie bilden ein gleichschenkliges Dreieck. Damit gilt:
$| \vec{A C} |$ $=$ $| \vec{A B} |$
$\sqrt{x^{2} + z^{2}}$ $=$ $\sqrt{3^{2} + 5^{2} + (- 4)^{2}}$
$\sqrt{x^{2} + z^{2}}$ $=$ $\sqrt{50}$ $()^{2}$
$x^{2} + z^{2}$ $=$ $50$
↓
Setze $x = \frac{4}{3} z$ ein.
$\frac{16}{9} z^{2} + z^{2}$ $=$ $50$
↓
Vereinfache
$\frac{25}{9} z^{2}$ $=$ $50$ $\cdot \frac{9}{25}$
$z^{2}$ $=$ $18$ $\sqrt{}$
$z$ $=$ $\pm \sqrt{18}$
Eine mögliche Lösung ist also $z = \pm \sqrt{18} = \pm 3 \sqrt{2}$ .
Bestimme den Punkt $C$
Mit der Gleichung $x = \frac{4}{3} z$ gilt für $x$ : $x = \pm \frac{4}{3} \sqrt{18} = \pm \frac{4}{3} 3 \sqrt{2} = \pm 4 \sqrt{2}$
Damit ist $C (\frac{4}{3} \sqrt{18} | 0 | \sqrt{18}) = C (4 \sqrt{2} | 0 | 3 \sqrt{2})$ oder $C (- \frac{4}{3} \sqrt{18} | 0 | - \sqrt{18}) = C (- 4 \sqrt{2} | 0 | - 3 \sqrt{2})$ .
Hinweis: Die Aufgabenstellung erfordert nur einen Punkt $C$ , hier wurden beide Möglichkeiten angegeben.
VorsichtAndere Darstellungen der Lösung
Je nachdem in welcher Reihenfolge $x$ und $z$ bestimmt werden, kann $C$ anders dargestellt sein. Ebenso korrekt wäre:
$C (\sqrt{32} | 0 | \frac{3}{4} \sqrt{32})$ bzw. $C (- \sqrt{32} | 0 | - \frac{3}{4} \sqrt{32})$ .
Verwende $\vec{A C} = (\begin{array}{c} x \\ 0 \\ z \end{array})$ als allgemeine Darstellung für die Kathete von $A$ nach $C$ , da die Kathete in der $x z$ -Ebene liegt.
Stelle 2 Gleichungen auf, um x und z zu bestimmen:
1. Gleichung: Stelle eine Gleichung auf, die das Skalarprodukt $\vec{A C} \cdot \vec{A B}$ enthält. (Die Katheten bilden einen rechten Winkel.)
2. Gleichung: Stelle eine weitere Gleichung auf, indem die Längen gleichgesetzt werden: $| \vec{A C} | = | \vec{A B} |$ . (Die Katheten sind gleich lang.)
Bestimme $x$ und $z$ aus den beiden Gleichungen. Stelle $C$ vollständig dar.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Bestimmung der Ableitung $f^{'} (x)$
	↓
$f^{'} (x)$	$=$	${(2 e^{x} - 4 e^{- x})}^{'}$
	↓	Summenrege l
	$=$	${(2 e^{x})}^{'} + {(- 4 e^{- x})}^{'}$
	↓	Die Ableitung von Vielfachen der e-Funktion $f (x) = a \cdot e^{x}$ ist $f^{'} (x) = a \cdot e^{x}$
	$=$	$2 e^{x} + {(- 4 e^{- x})}^{'}$
	↓	Kettenregel
	$=$	$2 e^{x} + {(- x)}^{'} \cdot (- 4 e^{- x})$
	$=$	$2 e^{x} + (- 1) \cdot (- 4 e^{- x})$
	$=$	$2 e^{x} + 4 e^{- x}$

Einsetzen von $x = 0$
	↓
$f^{'} (0)$	$=$	$2 e^{0} + 4 e^{- 0}$
	↓	$e^{0} = 1$
	$=$	$6$

Pflichtteil

Aufgabe 1

Flächenstück berechnen

Hast du eine Frage oder Feedback?

Flächeninhalt Quadrat:

Flächeninhalt des Flächenstücks zwischen Graph und x-Achse:

Gleichsetzen der Flächeninhalte:

Hast du eine Frage oder Feedback?

Aufgabe 2

Berechnung der Nullstelle

Hast du eine Frage oder Feedback?

Lösungsvorschlag

Steigung der Tangente:

y-Achsenabschnitt der Tangente

Geradengleichung der Tangente

Hast du eine Frage oder Feedback?

Aufgabe 3

Koordinaten des Punktes

Hast du eine Frage oder Feedback?

Anfertigen der Skizze

Hast du eine Frage oder Feedback?

Aufgabe 4

Baumdiagramm als Hilfe

Ereignis

Hast du eine Frage oder Feedback?

Wahrscheinlichkeiten $P (X = k)$

Aufstellen des Erwartungswertes

Hast du eine Frage oder Feedback?

Aufgabe 5

Gerade in Ebenengleichung einsetzen

Hast du eine Frage oder Feedback?

Untersuchen der Richtungsvektoren

Gleichsetzen der Geradengleichungen

Hast du eine Frage oder Feedback?

Aufgabe 6

1. Gleichung - rechtwinklige Katheten

2. Gleichung - Länge der Katheten

Bestimme den Punkt $C$

$A$	$=$	$\int_{0}^{2 a} f (x) d x$
	$=$	${[F (x)]}_{0}^{2 a}$
	↓	Bestimme eine Stammfunktion F(x). (Hilfe im Spoiler oben)
	$=$	${[- \frac{1}{3} x^{3} + a x^{2}]}_{0}^{2 a}$
	↓	Setze die Nullstellen ein. In die eckige Klammer wird für x der obere Wert (2a) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$- \frac{1}{3} \cdot {(2 a)}^{3} + a \cdot {(2 a)}^{2}$
	$=$	$- \frac{1}{3} \cdot 8^{} a^{3} + a \cdot 4 a^{2}$
	$=$	$- \frac{8}{3} a^{3} + 4 a^{3^{}}$
	$=$	$- \frac{8}{3} a^{3} + \frac{12}{3} a^{3}$
	$=$	$\frac{4}{3} a^{3}$

Wenn beide Flächeninhalte gleich sind, gilt:
	↓
$A_{Q u a d r a t}$	$=$	$A_{F l \ddot{a} c h e n s t \ddot{u} c k}$
	↓	Einsetzen der Terme für die Flächeninhalte
$a^{4}$	$=$	$\frac{4}{3} a^{3}$	$: (a^{3})$
	↓	Da $a > 1$ gilt, kann durch $a^{3}$ geteilt werden.
$a^{}$	$=$	$\frac{4}{3}$

Der Funktionswert $f (x)$ wird gleich $0$ gesetzt.
	↓
$f (x)$	$=$	$0$
$2 e^{x} - \frac{4}{e^{x}}$	$=$	$0$	$\cdot e^{x}$
$2 e^{2 x} - 4$	$=$	$0$	$+ 4$
$2 e^{2 x}$	$=$	$4$	$: 2$
$e^{2 x}$	$=$	$2$	$\ln ()$
$2 x$	$=$	$\ln (2)$	$: 2$
$x$	$=$	$\frac{1}{2} \ln (2)$

$f (x)$	$=$	$2 e^{x} - \frac{4}{e^{x}}$
	↓	im y-Achsenabschnitt gilt $x = 0$
$f (0)$	$=$	$2 e^{0} - \frac{4}{e^{0}}$
	↓	$e^{0} = 1$
	$=$	$- 2$

Stelle die allgemeine Geradengleichung auf und setze die Steigung und den y-Achsenabschnitt der Tangente ein.
	↓
$y$	$=$	$m x + b$
	↓	m ist die Steigung b ist der y-Achsenabschnitt
	$=$	$6 x - 2$

$2$	$=$	$x + y + z$
	↓	Setze die Gerade koordinatenweise in die Ebenengleichung ein
$2$	$=$	$s + 1 + (1 - s)$
	↓	Vereinfache
	$=$	$2$

Gleichsetzen
	↓
$(\begin{array}{l} 0 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$	$=$	$(\begin{array}{l} 0 \\ 0 \\ 1 \end{array}) + t \cdot (\begin{array}{l} 1 \\ a \\ 0 \end{array})$
	↓	Bringe alle Stützvektoren nach links und alle Richtungsvektoren nach rechts.
$(\begin{array}{l} 0 \\ 1 \\ 0 \end{array})$	$=$	$t \cdot (\begin{array}{l} 1 \\ a \\ 0 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array})$

$0$	$=$	$(\begin{array}{c} x \\ 0 \\ z \end{array}) \cdot (\begin{array}{c} 3 \\ 5 \\ - 4 \end{array})$
	↓	Skalarprodukt ausrechnen
$0$	$=$	$3 x - 4 z$

$\| \vec{A C} \|$	$=$	$\| \vec{A B} \|$
$\sqrt{x^{2} + z^{2}}$	$=$	$\sqrt{3^{2} + 5^{2} + (- 4)^{2}}$
$\sqrt{x^{2} + z^{2}}$	$=$	$\sqrt{50}$	$()^{2}$
$x^{2} + z^{2}$	$=$	$50$
	↓	Setze $x = \frac{4}{3} z$ ein.
$\frac{16}{9} z^{2} + z^{2}$	$=$	$50$
	↓	Vereinfache
$\frac{25}{9} z^{2}$	$=$	$50$	$\cdot \frac{9}{25}$
$z^{2}$	$=$	$18$	$\sqrt{}$
$z$	$=$	$\pm \sqrt{18}$

Pflichtteil

Aufgabe 1

Flächenstück berechnen

Hast du eine Frage oder Feedback?

Flächeninhalt Quadrat:

Flächeninhalt des Flächenstücks zwischen Graph und x-Achse:

Gleichsetzen der Flächeninhalte:

Hast du eine Frage oder Feedback?

Aufgabe 2

Berechnung der Nullstelle

Hast du eine Frage oder Feedback?

Lösungsvorschlag

Steigung der Tangente:

y-Achsenabschnitt der Tangente

Geradengleichung der Tangente

Hast du eine Frage oder Feedback?

Aufgabe 3

Koordinaten des Punktes

Hast du eine Frage oder Feedback?

Anfertigen der Skizze

Hast du eine Frage oder Feedback?

Aufgabe 4

Baumdiagramm als Hilfe

Ereignis

Hast du eine Frage oder Feedback?

Wahrscheinlichkeiten P(X=k)

Aufstellen des Erwartungswertes

Hast du eine Frage oder Feedback?

Aufgabe 5

Gerade in Ebenengleichung einsetzen

Hast du eine Frage oder Feedback?

Untersuchen der Richtungsvektoren

Gleichsetzen der Geradengleichungen

Hast du eine Frage oder Feedback?

Aufgabe 6

1. Gleichung - rechtwinklige Katheten

2. Gleichung - Länge der Katheten

Bestimme den Punkt C

Wahrscheinlichkeiten $P (X = k)$

Bestimme den Punkt $C$