Allgemeine Aufgaben zur Wahrscheinlichkeit
- 1
Auf einer Fähre befinden sich 20 Personen. Zwei Personen haben Schmuggelware dabei, einer dieser Schmuggler ist Felix. Ein Zollbeamter ruft der Reihe nach 3 Personen zur Kontrolle von der Fähre herunter. Wie groß ist die Wahrscheinlichkeit dafür, dass
mindestens einer der Schmuggler entdeckt wird?
%Felix entdeckt wird?
%beide Schmuggler bei dieser Kontrolle entdeckt werden?
%
- 2
Gegeben ist: ; ;
Berechne:
- 3
Drücke die Wahrscheinlichkeit für das Ereignis durch die Wahrscheinlichkeiten der Ereignisse , und aus.
- 4
Gegeben: ; ;
Berechne:
- 5
Zwei Jungen und drei Mädchen sind eingeladen. Sie treffen nacheinander ein. Jede Reihenfolge ist gleich wahrscheinlich. Wie groß ist die Wahrscheinlichkeit, dass
abwechselnd ein Junge und ein Mädchen eintreffen
%die drei Mädchen direkt nacheinander eintreffen?
%
- 6
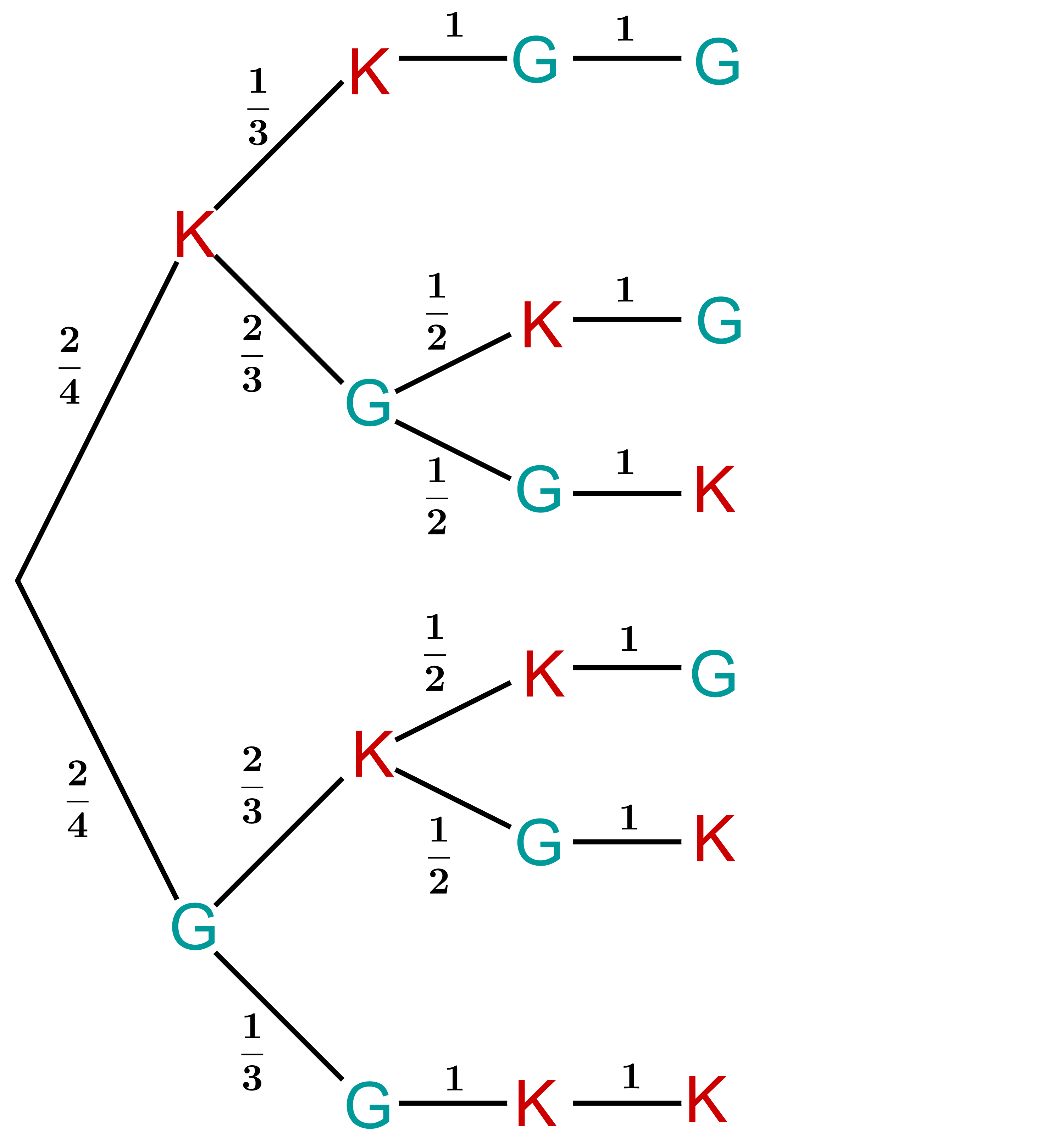
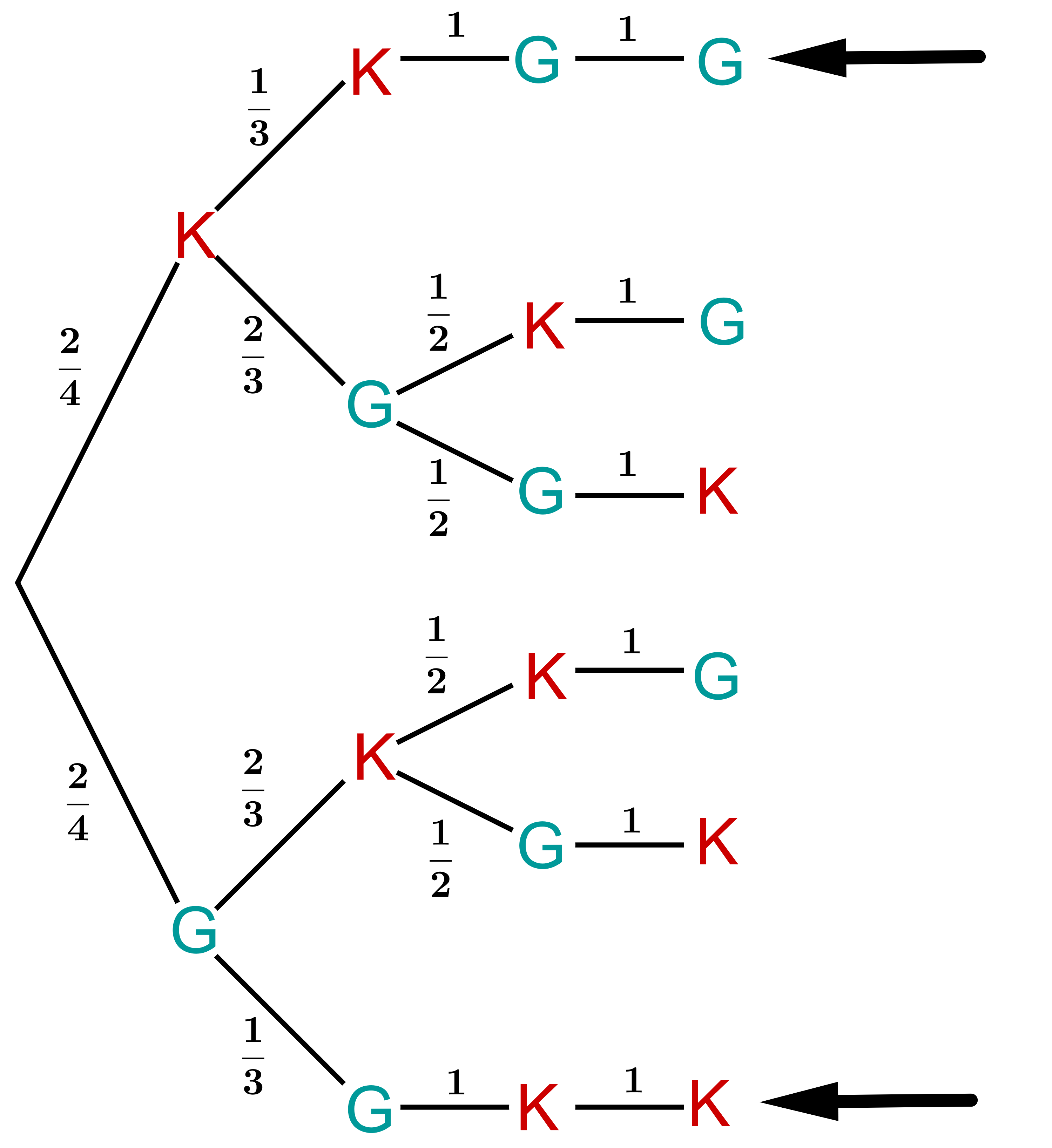
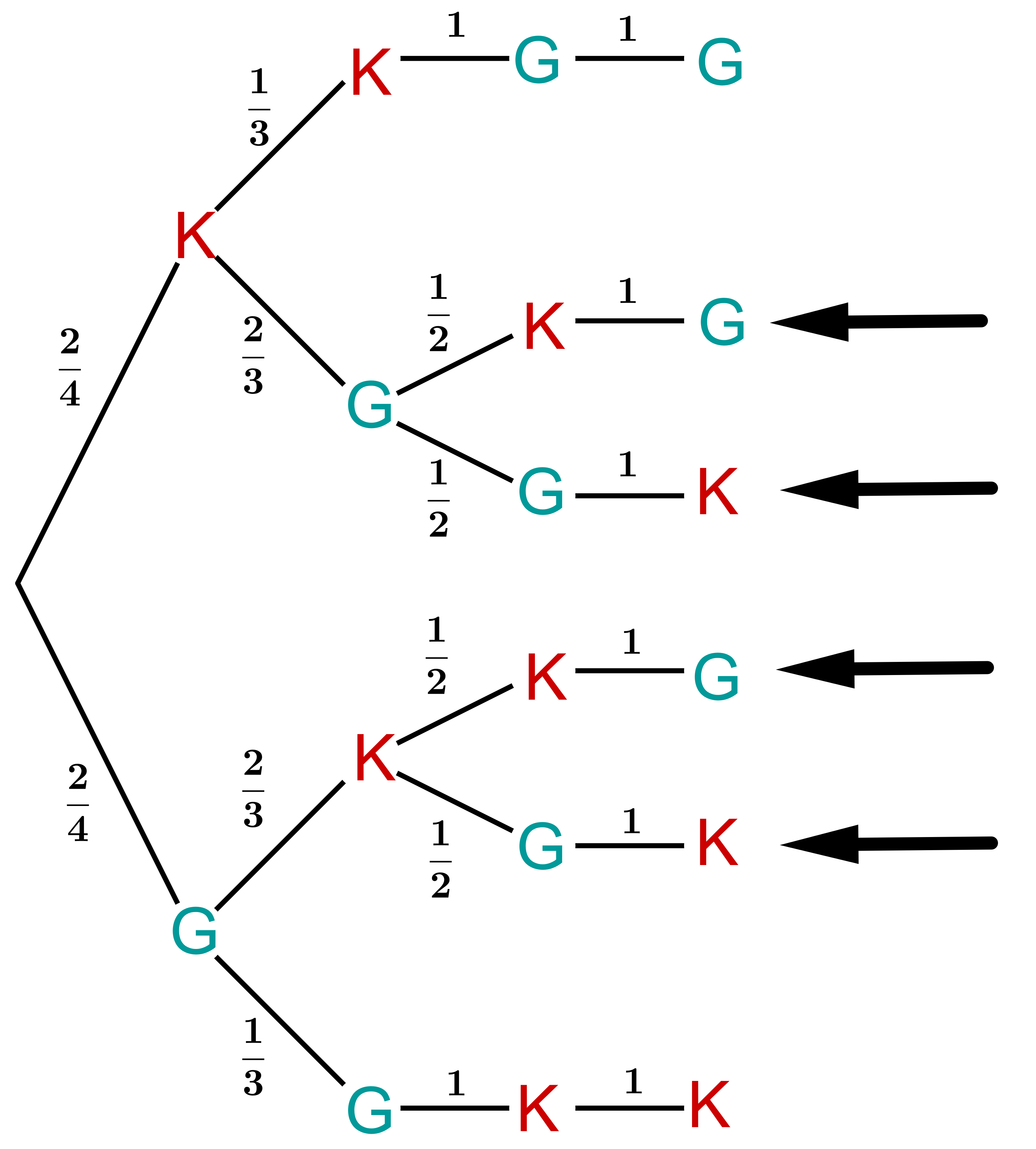
Zwei defekte Computermonitore sind mit zwei guten zusammengepackt worden. Man prüft die Monitore der Reihe nach, bis man weiß, welche die zwei fehlerhaften sind. Mit welcher Wahrscheinlichkeit ist man nach Prüfung des zweiten Monitors, mit welcher Wahrscheinlichkeit erst nach Prüfung des dritten fertig?
- 7
In einer Gruppe sind 5 Franzosen, 6 Spanier und 10 Schweizer. Zwei Personen werden zufällig ausgelost. Wie hoch ist die Wahrscheinlichkeit, dass genau ein Schweizer ausgelost wird?
% - 8
Aus den abgebildeten Netzen lassen sich „Spielwürfel“ mit und Seitenflächen erstellen.
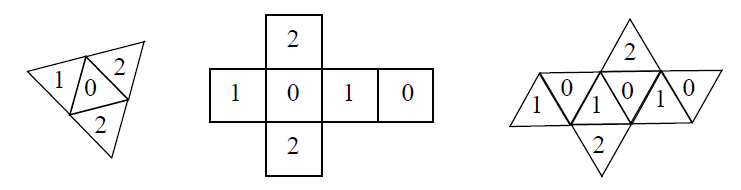
Welche Wahrscheinlichkeiten erhältst du für die Augenzahlen und bei den verschiedenen „Spielwürfeln“, wenn du sehr oft würfelst?
Bei einem Spiel würfelt jeder Teilnehmer so lange, bis er zum ersten Mal eine „“ geworfen hat. Wer am wenigsten Würfe benötigt, gewinnt. Welchen Würfel würdest du für dieses Spiel auswählen? Erläutere deine Entscheidung.
Bei einem anderen Spiel wird reihum gewürfelt. Wer eine „“ würfelt, scheidet aus. Wie groß ist mit den verschiedenen Würfeln jeweils die Chance, bei einem Wurf keine „“ zu werfen?
Bei tausend Würfen mit einem der drei Würfel hat sich folgendes Ergebnis ergeben:
Augenzahl
0
1
2
absolute Häufigkeit
241
253
506
Was meinst du, welcher Würfel verwendet wurde? Erläutere deine Antwort.
- 9
Ein Zufallsexperiment hat die vier Elementarereignisse
Außerdem sind die Wahrscheinlichkeiten von drei Ereignissen
bis gegeben.
;
;
;
Begründe, dass diese Wahrscheinlichkeitsverteilung unzulässig ist.
Ändere so ab, dass die Wahrscheinlichkeitsverteilung zulässig ist.
Berechne unter der Voraussetzung, dass mit einer doppelt so hohen Wahrscheinlichkeit auftritt wie .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?