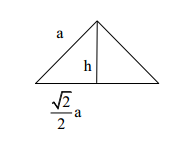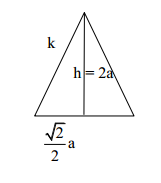Aufgaben zu Volumen und Oberflächenberechnung
- 1
Ein rechteckiger Wasserbehälter mit den Maßen soll mit Wasser gefüllt werden.
Wie viel Liter kann er fassen?
l - 2
Berechne Volumen und Masse des Stahlteils. Alle Längen sind in Millimeter angegeben.
Dichte:

- 3
Berechne Volumen und Masse des Kupferteils. Das Material ist 12 mm dick.
Dichte:

- 4
Ein Stahlrohr ist 10 m lang (), hat einen Außendurchmesser von und einen Innendurchmesser von .
Berechnen Sie das Volumen, die Masse und die Wandstärke des Rohres.

- 5
Eine gerade Pyramide hat als Grundfläche ein Rechteck mit den Seitenlängen und . Die Höhe der Pyramide beträgt .
Berechne die Kantenlängen als Vielfache von .
Berechne den Oberflächeninhalt der Pyramide in Vielfachen von .
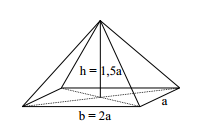
- 6
Eine gerade Pyramide hat als Grundfläche ein gleichseitiges Dreieck mit der Kantenlänge a. Die Höhe der Pyramide beträgt 2a. Berechne die Seitenkantenlängen in Vielfachen von a. Berechne den Oberflächeninhalt der Pyramide in Vielfachen von a.
- 7
Die rechteckige Grundfläche eines Ölbehälters hat die Maße a=60cm und b=40cm.
Der Behälter ist mit V=140 Liter Öl gefüllt.
Welche Höhe h hat der Ölspiegel in ganzen cm?
cm - 8
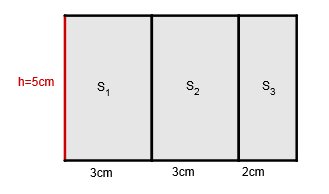
Die nebenstehende Figur rotiert um die Achse A.
Berechne das Volumen des Rotationskörpers in Abhängigkeit von a.

- 9
Berechne Volumen und Oberfläche, wenn der Körper jeweils die Höhe hat:
Prisma mit gleichschenkligem Dreieck als Grundfläche, Schenkellänge und Basis .
Zylinder mit Radius
Gerade Pyramide (alle Seitenkanten gleich lang) mit Quadrat der Kantenlänge als Grundfläche.
Kegel mit Radius
- 10
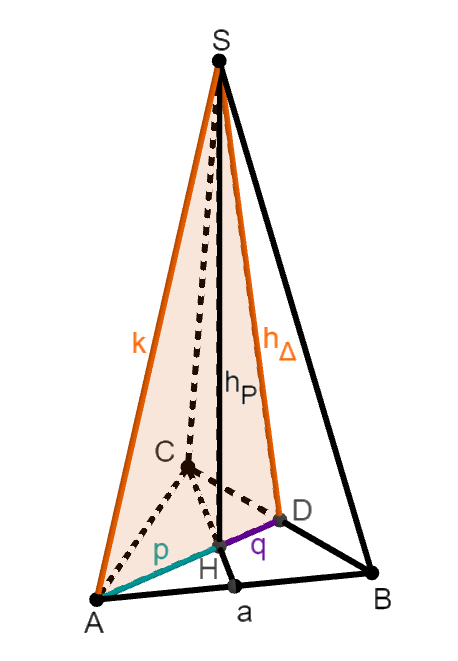
Das Bild zeigt eine gerade Pyramide mit einem Quadrat als Grundfläche. Der Punkt halbiert die Höhe .
Die Winkel im Dreieck hängen nicht von ab.
Berechne jeweils in Abhängigkeit von
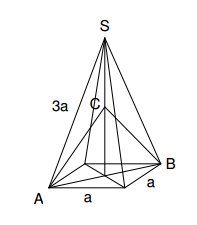
Das Volumen der Pyramide
Den Oberflächeninhalt der Pyramide
Die drei Seitenlängen im Dreieck .
Die Winkel im Dreieck .
Den Flächeninhalt des Dreiecks .
- 11
Das Bild zeigt eine gerade Pyramide mit einem Quadrat der Kantenlänge als Grundfläche. Die Seitenkanten haben ebenfalls die Länge .
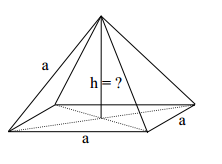
Zeichne ein Netz der Pyramide für .
Berechne die Höhe der Pyramide in Vielfachen von .
Berechne den Oberflächeninhalt der Pyramide
- 12
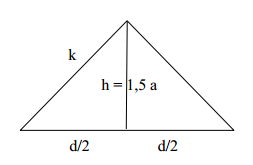
Das Bild zeigt eine gerade Pyramide mit einem Quadrat der Kantenlänge als Grundfläche. Die Höhe der Pyramide ist .
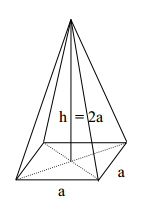
Berechne die Länge der Seitenkanten in Vielfachen von .
Berechne den Oberflächeninhalt der Pyramide in Vielfachen von .
Bestimme auf Millimeter genau, wenn der Oberflächeninhalt genau betragen soll.
- 13
Ein Würfel und eine gerade Pyramide haben jeweils ein Quadrat der Kantenlänge als Grundfläche. Beide Körper sollen den gleichen Oberflächeninhalt haben.
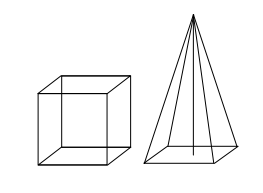
Wie lang müssen dann die Seitenkanten der Pyramide sein?
Berechne auch die Höhe der Pyramide.
- 14
Das Bild zeigt eine gerade Pyramide mit einem Quadrat als Grundfläche. Der Punkt halbiert die Höhe .
Die Winkel im Dreieck hängen nicht von ab.
Berechne jeweils in Abhängigkeit von
Das Volumen der Pyramide
Den Oberflächeninhalt der Pyramide
Die drei Seitenlängen im Dreieck
Die Winkel im Dreieck
Den Flächeninhalt des Dreiecks
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?