Aufgaben zu den binomischen Formeln
Hier findest du Aufgaben zu den binomischen Formeln. Lerne, binomische Formeln anzuwenden und vertiefe dein Wissen!
- 1
- 2
- 3
Was ergibt ?
- 4
Welche der folgenden Terme sind zum Term äquivalent?
- 5
Löse auf (Binome)
- 6
Schreibe ohne Klammern
- 7
Vereinfache
- 8
Kann man die binomische Formel anwenden? Wenn ja, wende sie an.
- 9
Multipliziere aus und fasse neu zusammen:
- 10
- 11
Verwandle in ein Produkt.
- 12
Faktorisiere
- 13
Fasse folgende Binome zusammen.
- 14
Benutze binomische Formeln um die Brüche zu kürzen
- 15
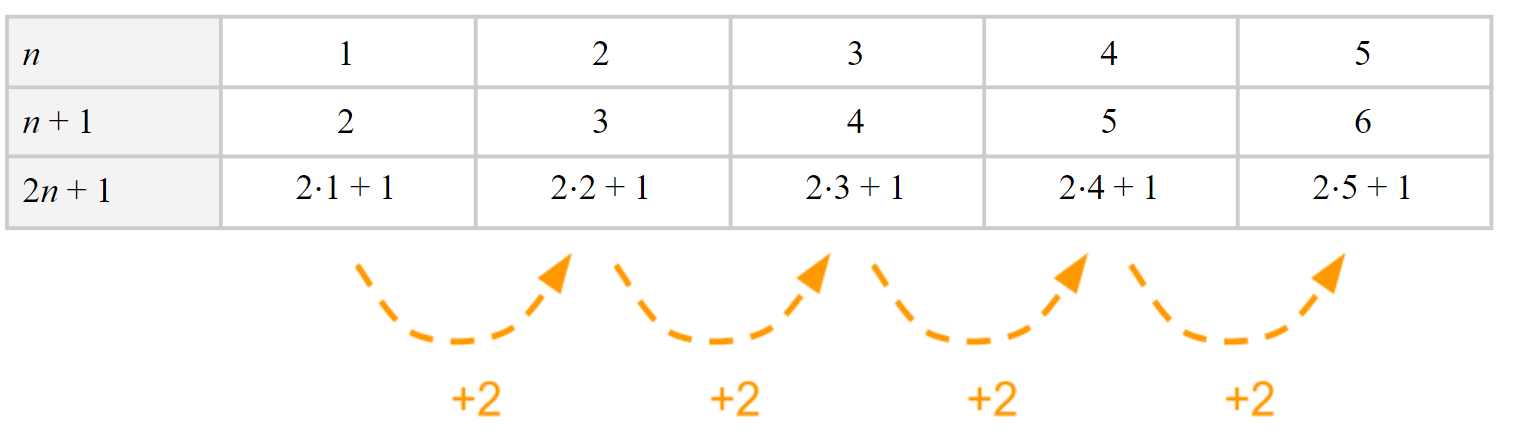
Beim Betrachten der Quadratzahlen fällt auf, dass die Differenz von jeweils zwei benachbarten Quadratzahlen immer um wächst:
,
dann ,
dann ,
dann ,
dann
usw.
Erkläre diesen Zusammenhang mit Hilfe einer binomischen Formel!
- 16
Interpretiere die Skizze als verallgemeinerte binomische Formel . Berechne entsprechend .
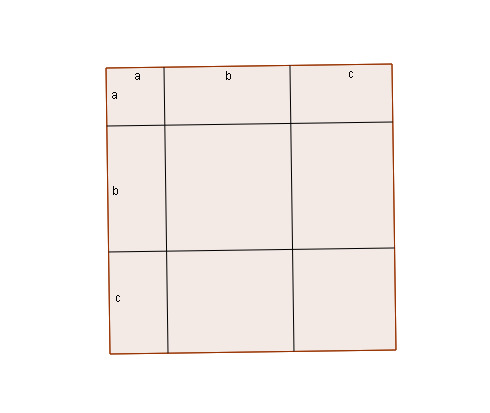
- 17
Klammere gemeinsame Faktoren aus.
- 18
Löse die Klammern auf. Fasse so weit wie möglich zusammen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?