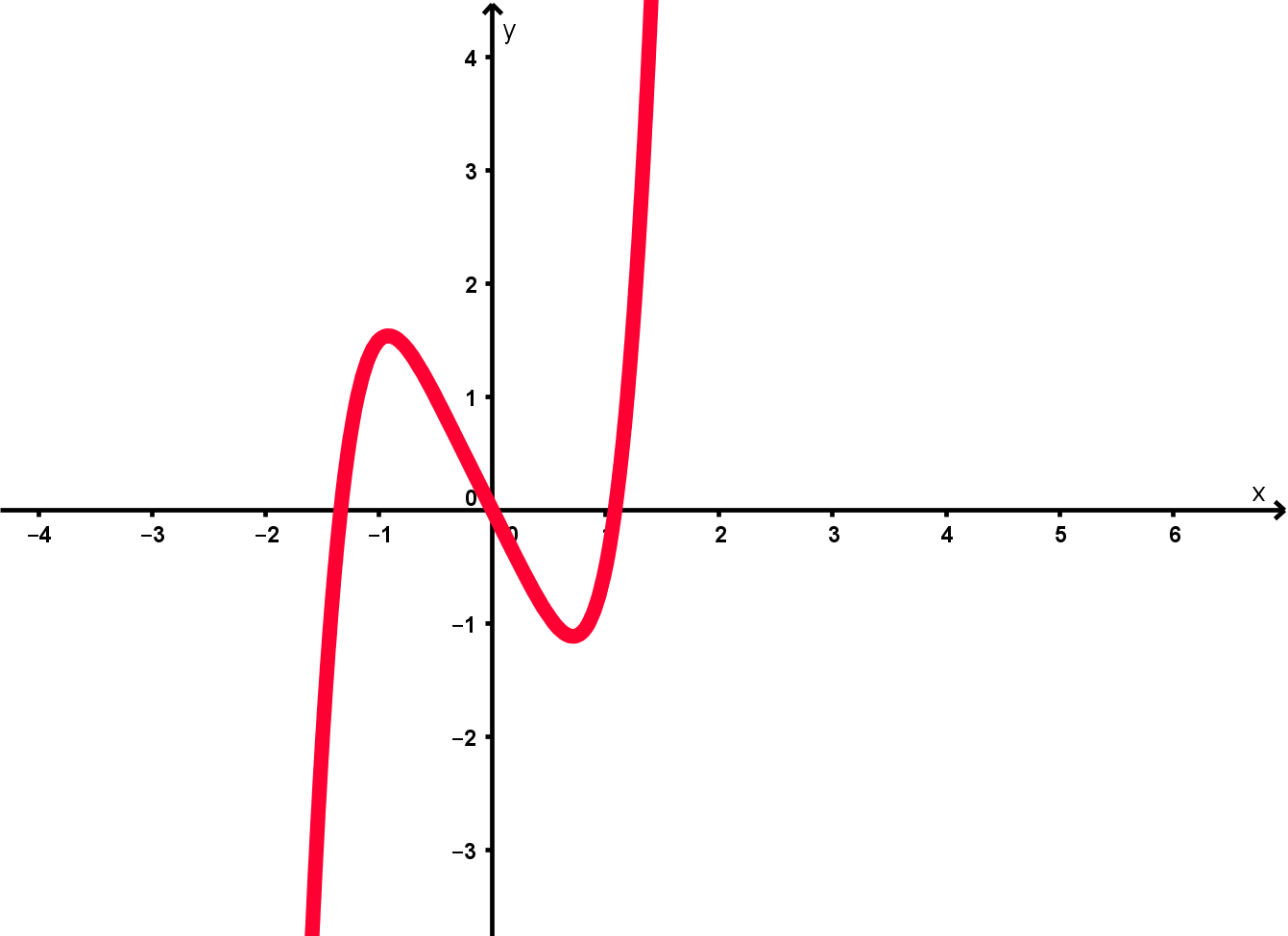
Aufgaben zu Polynomfunktionen

1
Beschreibe den charakteristischen Verlauf der folgenden Funktionen.
1. $f(x) = -9x^2 + 7x -3$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
  Der charakteristische Verlauf einer Polynomfunktion kann mit ein paar Regeln vorhergesagt werden.
  $f$ ist eine eine quadratische Funktion, da der größte Exponent $2$ ist. Wir wissen, dass das Verhalten im Unendlichen vom Grad des Polynoms, sowie vom Vorzeichen des ersten Koeffizienten (nach Sortierung der Terme nach fallenden Exponenten) abhängt.
  Für sehr kleine Werte von $x$ (damit sind negative $x$ -Werte mit sehr großem Betrag gemeint), sowie sehr große Werte von $x$ dominiert also der Term $-9x^2$ . Dieser ist negativ für jedes $x$ . Damit ist der charakteristische Verlauf der Funktion $f$ :
  "Von links unten nach rechts unten".
  Also ungefähr so:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f(x)=2x^2+3x^6+1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
  Der charakteristische Verlauf einer Polynomfunktion hängt vom Grad der Polynomfunktion und vom Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten ab.
  $f(x)=2x^2+3x^6+1$
  Sortiere den Term nach fallenden Exponenten.
  $f(x)=3x^6+2x^2+1$
  Lese den Grad der Funktion und das Vorzeichen des ersten Koeffizienten ab.
  Die Funktion hat den Grad $6$ und das Vorzeichen des ersten Koeffizienten (nach der Sortierung) ist positiv.
  Für sehr kleine Werte von $x$ (damit sind negative $x$ -Werte mit sehr großem Betrag gemeint), sowie sehr große Werte von $x$ dominiert also der Term $3x^6$ . Dieser ist positiv für jedes $x$ . Damit ist der charakteristische Verlauf der Funktion $f$ von links oben nach rechts oben.
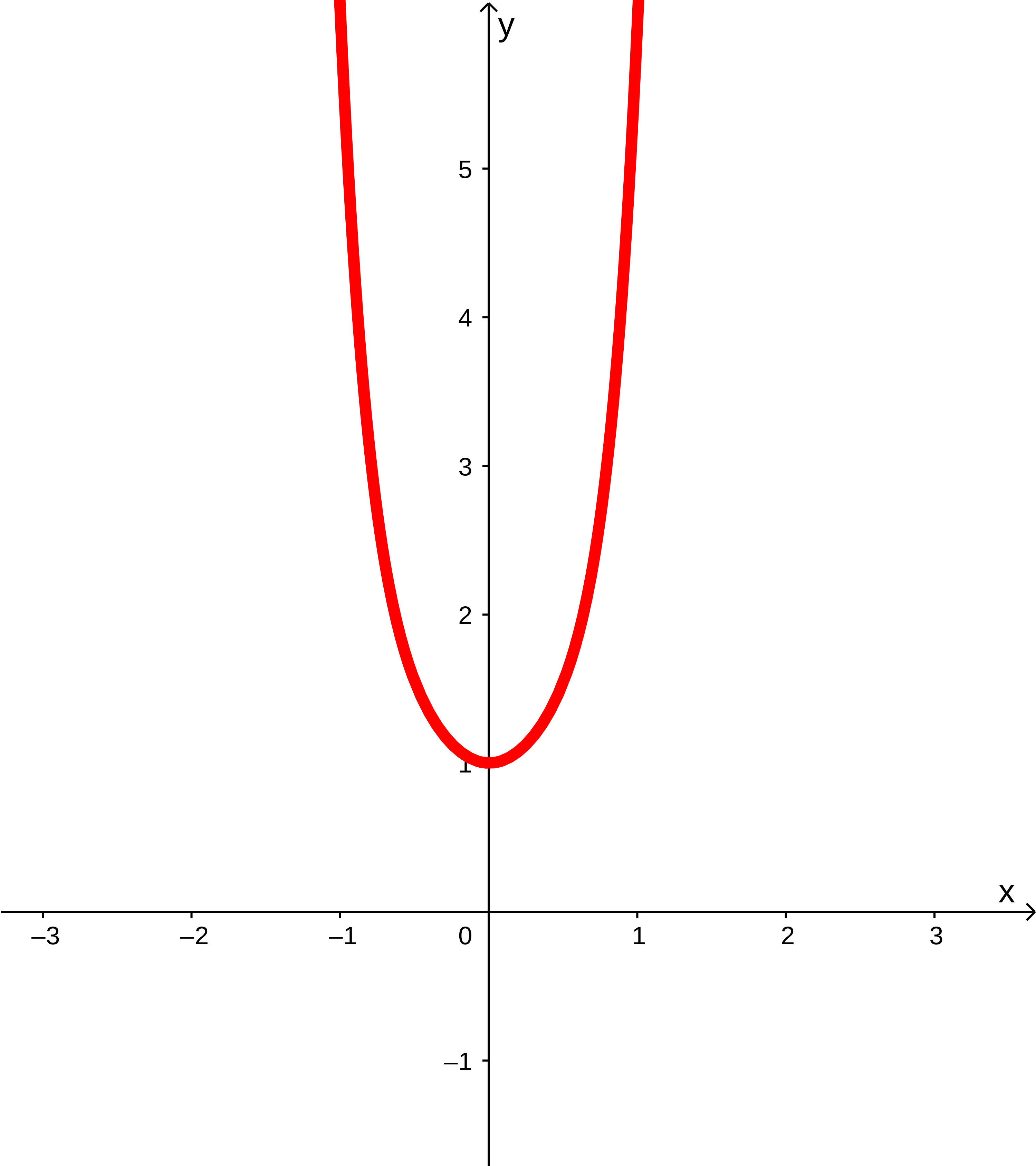
  Da die Polynomfunktion nur Potenzen mit geradem Exponenten enthält, ist die Funktion symmetrisch zur y-Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f(x)=(x-3)(x+4)(2-x)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
  Der charakteristische Verlauf einer Polynomfunktion hängt vom Grad der Polynomfunktion und vom Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten ab.
  $f(x)=(x-3)(x+4)(2-x)$
  Der Grad der Funktion f(x) ergibt sich aus der Summe der Grade der einzelnen Faktoren.
  f ist das Produkt von drei Linearfaktoren. Alle drei Faktoren haben den Grad 1.
  Grad $f(x) =1+1+1=3$
  Somit ist f ein Polynom dritten Grades.
  In den Faktoren taucht die Variable x zweimal mit positivem Vorzeichen und einmal mit negativem Vorzeichen auf. Das Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten $x^3$ ist also negativ.
  $-x^3$ ist positiv, wenn $x$ negativ ist und negativ, wenn $x$ positiv ist.
  Damit ist der charakteristische Verlauf der Funktion $f$ von links oben nach rechts unten.
  Da die Polynomfuktion sowohl Potenzen mit geradem als auch ungeradem Exponenten enthält, ist die Funktion weder symmetrisch zur y-Achse noch punktsymmetrisch.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $g(x) = (x-1)(x+3)^2(x+1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
  Erste Variante:
  $\def\arraystretch{1.25} \begin{array}{rcl}g(x)&=&(x-1)(x+3)^2(x+1)\end{array}$
  Zuerst wird $(x+3)^2$ ausmultipliziert.
  $\def\arraystretch{1.25} \begin{array}{rcl} && &=& (x-1)(x^2+6x+9)(x+1) \end{array}$
  Jetzt kannst Du die linke und die mittlere Klammer ausmultiplizieren.
  $\def\arraystretch{1.25} \begin{array}{rcl} && &=& (x^3 + 5x^2 +3x -9)(x+1)\end{array}$
  Als letztes wird die rechte Klammer multipliziert.
  $\def\arraystretch{1.25} \begin{array}{rcl} && &=& x^4 +6x^3 +8x^2 -6x -9\end{array}$
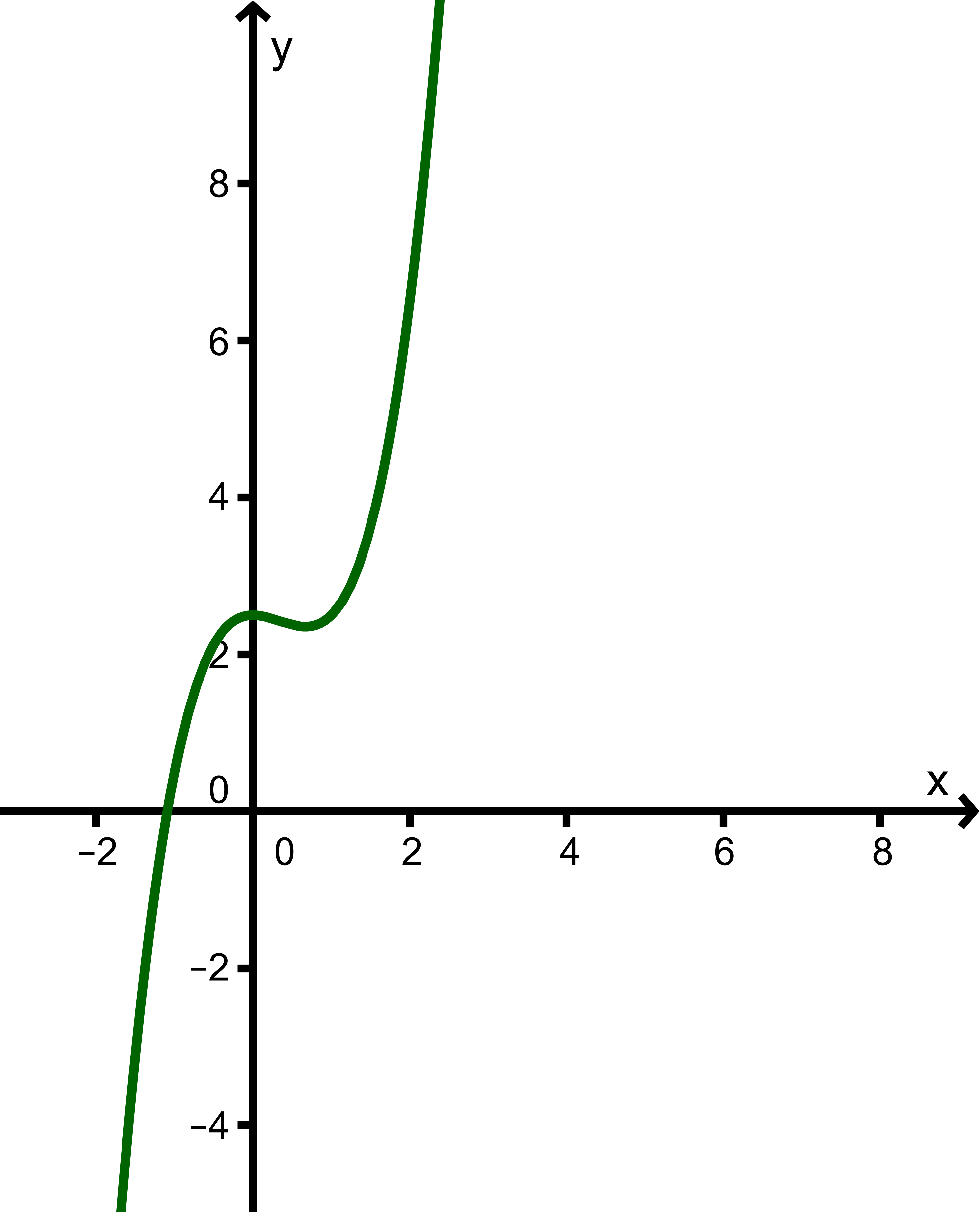
  Jetzt hat $g$ eine schöne Gestalt, an der der charakteristische Verlauf abgelesen werden kann. Der Grad der Funktion $g$ ist $4$ . Der Term $x^4$ dominiert also für große Werte von $x$ . Da der Koeffizient vor dem $x^4$ gleich $+1$ ist und $x^4$ selbst positiv ist für alle $x$ , hat $g$ den charakteristischen Verlauf "Von links oben nach rechts oben".
  Zweite Variante (etwas fortgeschrittener):
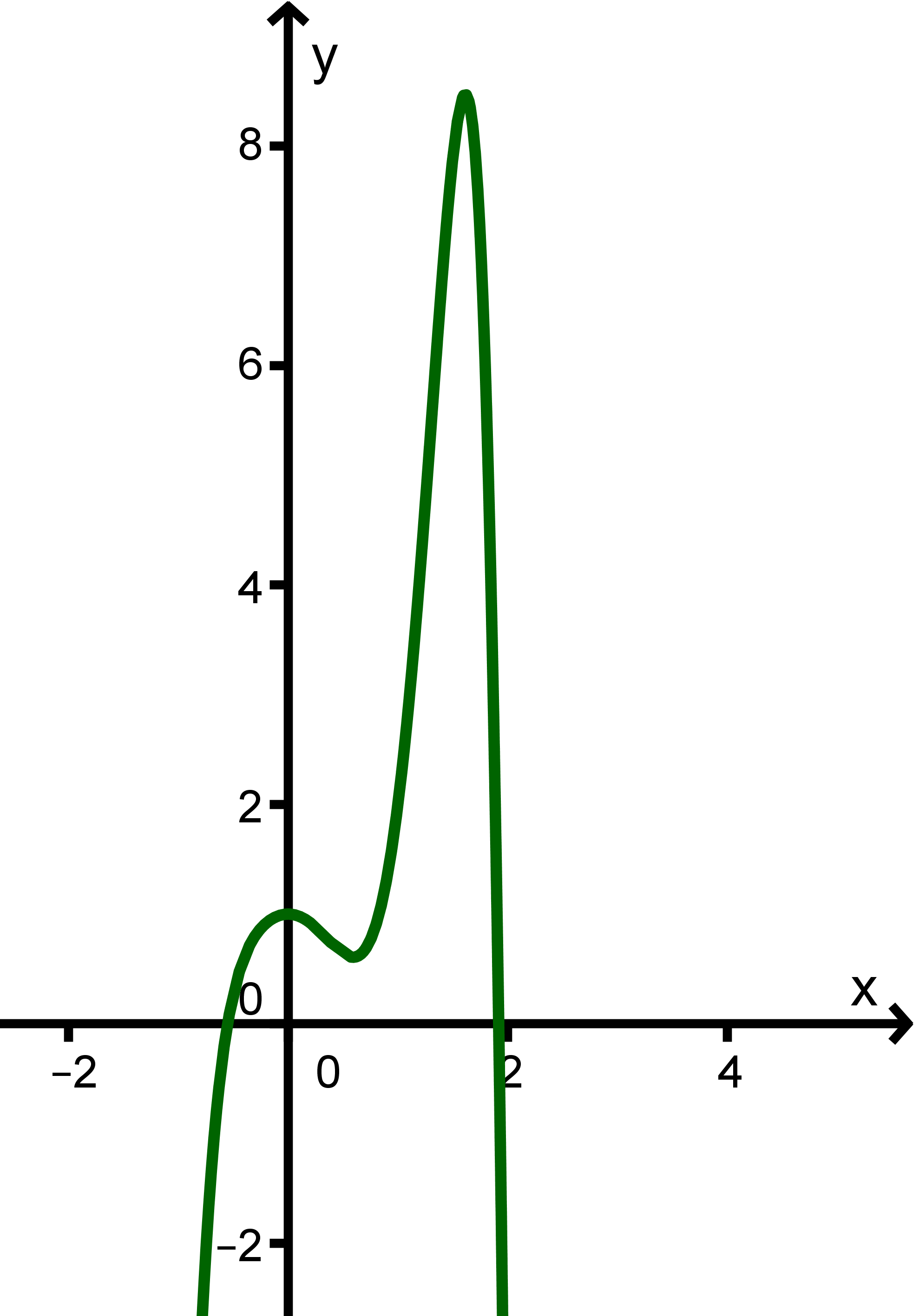
  Zuerst ermittelst Du den Grad dieser Funktion ohne ausmultiplizieren der Terme. Da $g$ das Produkt von vier Linearfaktoren ist ( der Faktor $(x+3)$ hat den Exponenten $2$ ) ist $g$ ein Polynom vierten Grades. In allen Faktoren taucht die Variable $x$ mit positivem Vorzeichen auf. Diese zwei Informationen genügen um den charakteristischen Verlauf von $g$ angeben zu können. Dieser ist nämlich "Von links oben, nach rechts oben".
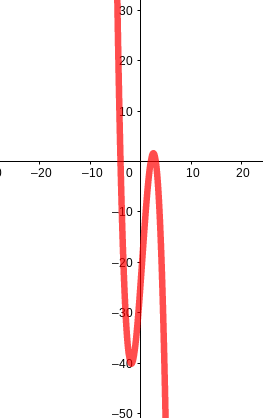
  Der Graph von $f$ sieht so aus:
  (Anmerkung: Das Bild zeigt den "genauen" Verlauf des Graphen von $f$ und nicht nur einen ungefähren Verlauf; selbstverständlich kannst du die Einzelheiten (z. B. wie tief der Graph nach unten geht usw.) aus der obigen Betrachtung allein noch nicht wissen.)
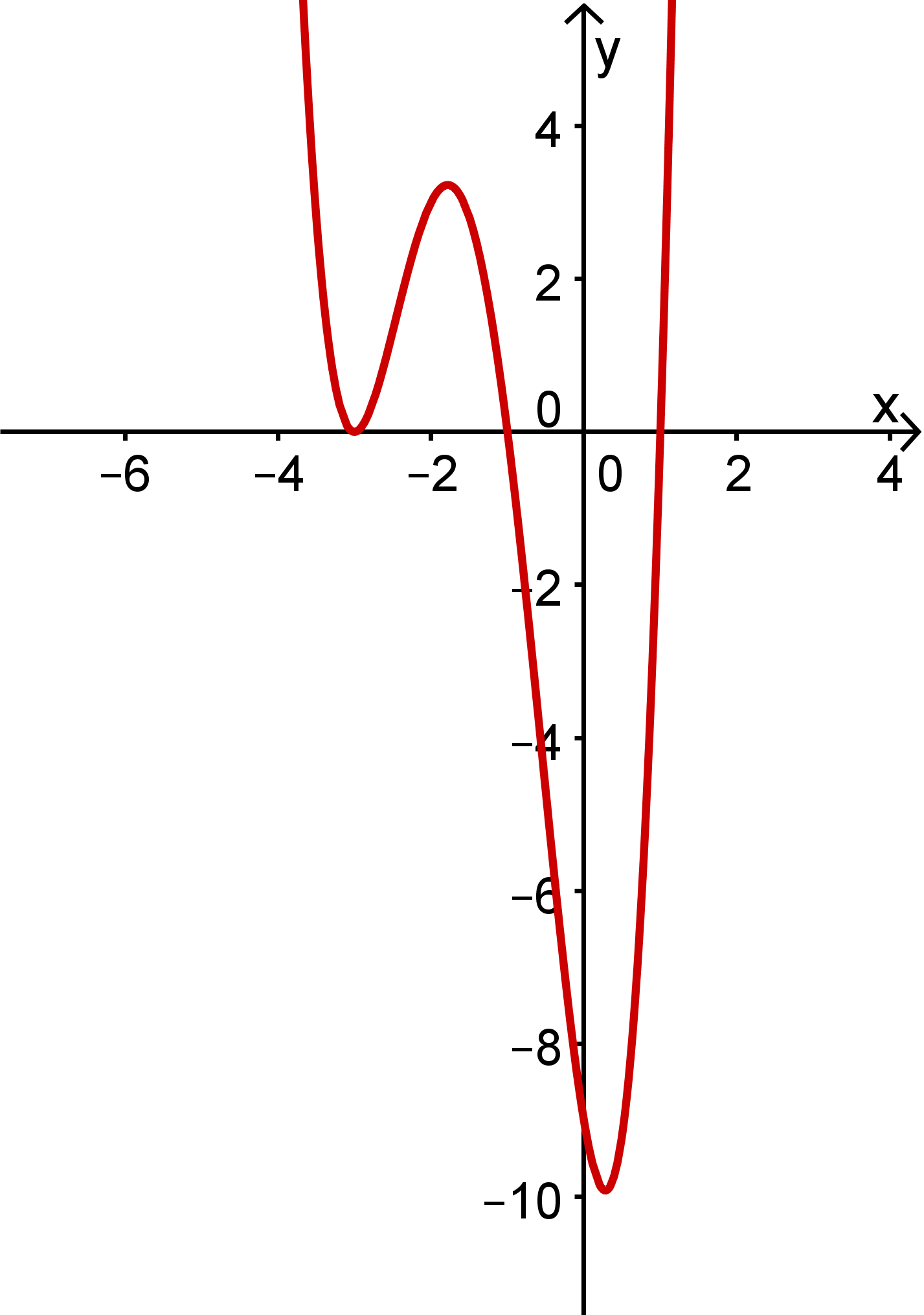
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $h(x) = 3x(1-x^2)^2(x+7)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
  Bei der Funktion $h$ muss man etwas vorsichtiger sein. Es scheint so als wäre $h$ in Linearfaktoren zerlegt, doch wenn man genauer hinschaut fällt auf, dass die mittlere Klammer $(1-x^2)^2$ kein Linearfaktor ist. Dort taucht ein $\bold x^{2}$ auf!
  Das ist nicht schlimm. Weil wir aber diese Klammer nicht ausmultiplizieren wollen ( "Mathematiker sind faul" ), musst Du dir ein paar Überlegungen für dieses Polynom machen.
  Was solltest Du über $(1-x^2)^2$ zu wissen?
  Man braucht ja schließlich den größten Exponenten, der nach ausmultiplizieren der Klammer bleibt. Dieser berechnet sich als das Produkt vom größten Exponenten in der Klammer mit dem Exponenten der Klammer. In unserem Fall wird also $4 = 2·2$ , der größte Exponent in $(1-x^2)^2$ sein.
  Stellen wir uns das Ausmultiplizieren der Klammer im Kopf vor, so stellen wir fest: Nur indem wir $-x^2$ mit sich selbst multiplizieren, erreichen wir die Potenz $x^4$ .
  Somit ist der Koeffizient vor dieser Potenz gleich $1 = (-1)^2$ .
  Jetzt können wir endlich weiterrechnen :)
  Weiter geht's mit $h$
  Da $h$ das Produkt von drei Funktionen ist, erhalten wir den Grad von $h$ indem wir die Grade dieser Funktionen aufsummieren. Der Grad von $h$ ist also $6 = 1+4+1$ . Der Koeffizient vor der größten Potenz in $h$ ist das Produkt der Koeffizienten vor den größten Potenzen in den einzelnen Faktoren. Wir berechnen also $3·1·1 = 3$ .
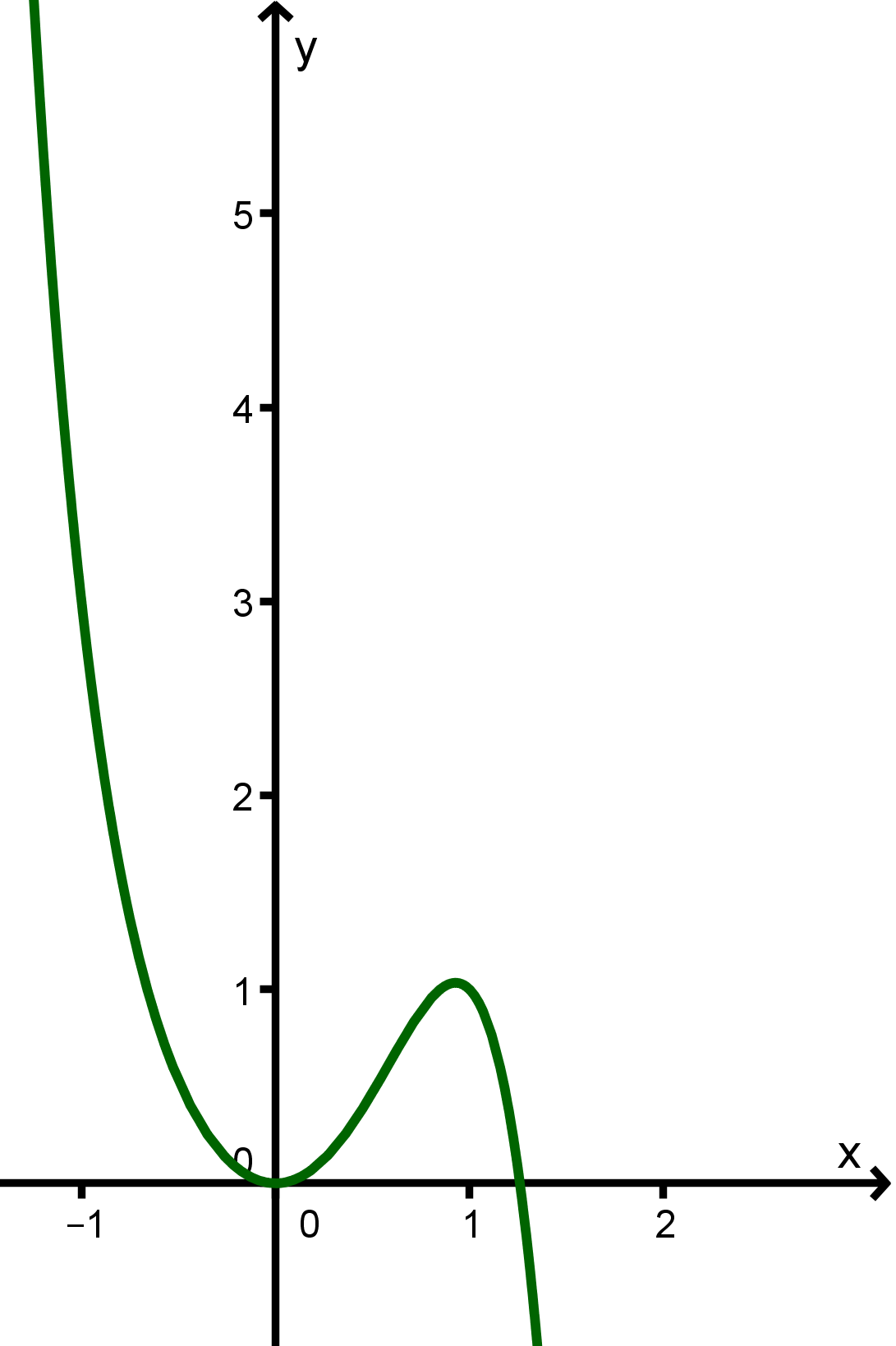
  Die Funktion $h$ sieht also so aus: $h(x) = 3x^6 + …$ wobei " … " dafür steht, dass wir Terme mit niedrigeren Exponenten einfach ignorieren.
  Da $h$ einen geraden Grad hat und ihr erster Koeffizient positiv ist, ist ihr charakteristischer Verlauf "Von links oben nach rechts oben".
  Also ungefähr so:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. $f(x)=(x+1)(2-x)(1+x^2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
  Wir wissen, dass der charakteristische Verlauf einer Polynomfunktion vom Grad der Polynomfunktion und vom Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten abhängt.
  Der Grad der Funktion f(x) ergibt sich aus der Summe der Grade der einzelnen Faktoren.
  $f(x)=(x+1)(2-x)(1+x^2)$
  f ist das Produkt von drei Linearfaktoren. Die ersten beiden Faktoren haben den Grad 1, der dritte Faktor hat den Grad 2.
  Grad $f(x) =1+1+2=4$
  Somit ist f ein Polynom vierten Grades.
  In den Faktoren taucht die Variable x zweimal mit positivem Vorzeichen und einmal mit negativem Vorzeichen auf. Das Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten $x^4$ ist also negativ.
  $-x^4$ ist negativ, wenn $x$ negativ ist und negativ, wenn $x$ positiv ist.
  Damit ist der charakteristische Verlauf der Funktion $f$ von links unten nach rechts unten.
  Da die Polynomfuktion sowohl Potenzen mit geradem als auch ungeradem Exponenten enthält, ist die Funktion weder symmetrisch zur Y-Achse noch punktsymmetrisch.
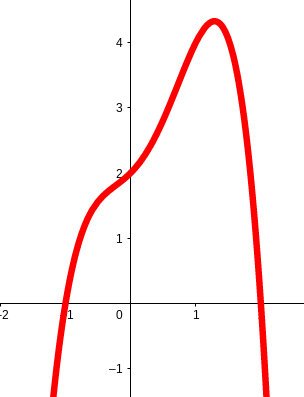
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. $i(x)=-5x^k-(x-1)^{k+1}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
  Tipp: Lass dich vom $k$ nicht abschrecken ;) Setze doch mal einen Wert für $k$ ein ( z. B. $k = 1$ ) und schaue wie der charakteristische Verlauf in diesem Fall wäre. Bleibt der Verlauf dann gleich, wenn man andere Werte für $k$ wählt? Lassen sich Aussagen für allgemeinere Werte von $k$ machen?
  Die Funktion $i$ erfordert zusätzliche Überlegungen gegenüber den anderen, denn $k$ ist kein fester Wert. Es liegt an uns zu untersuchen, was für verschiedene Werte von $k$ mit der Funktion $i$ passiert.
  Doch bevor wir loslegen, schauen wir uns $i$ nochmal genauer an. Der Grad von $i$ ist gleich $k+1$ , denn $k+1$ ist immer größer als $k$ . Das erspart uns schon mal einiges an Arbeit. Wir wissen ja, dass nur der Teil mit der größten Potenz für den charakteristischen Verlauf von Bedeutung ist.
  Wie ist dann der charakteristische Verlauf vom Term $-(x-1)^{k+1}$ ?
  Nach dem Ausmultiplizieren des Terms ist der Summand mit dem größten Exponenten $-x^{k+1}$ Hier müssen wir wirklich unterscheiden, was für verschiedene Werte von $k$ passiert.
  Wenn $k$ ungerade ist, dann ist der Exponent $k+1$ gerade. Der Koeffizient vor der größten Potenz von x ist gleich $-1$ . Somit hat $i$ für $k$ ungerade den charakteristischen Verlauf "von links unten nach rechts unten".
  Also ungefähr so:
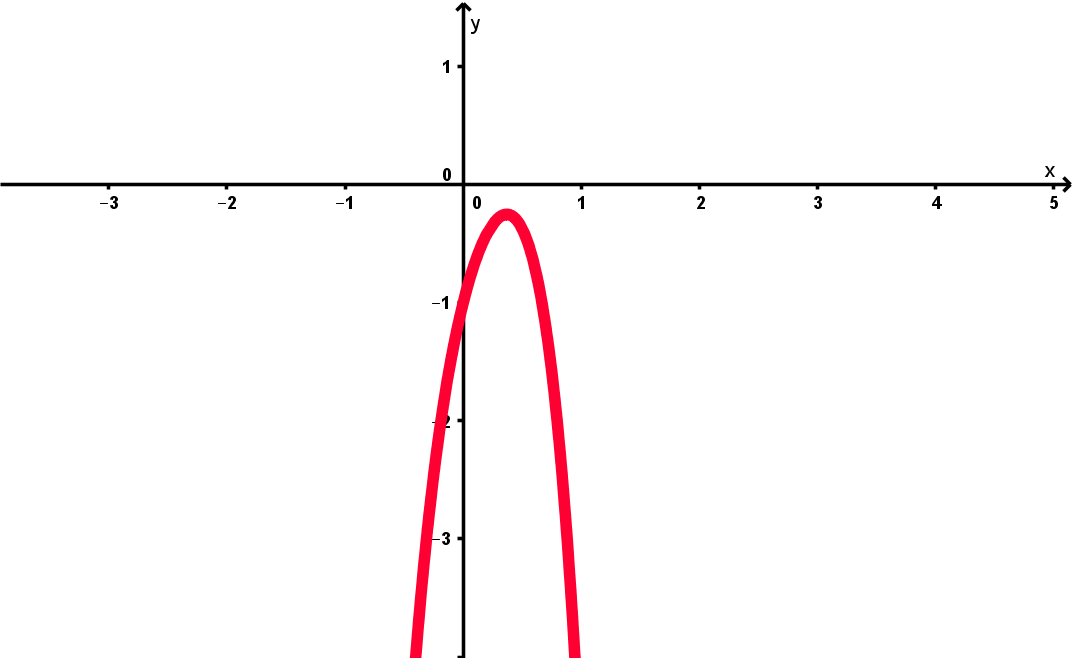
  Wenn $k$ gerade ist, dann ist der Exponent $k+1$ ungerade. Der Koeffizient vor der größten Potenz von x ist weiterhin gleich $-1$ . Somit ist der charakteristische Verlauf von $i$ "von links oben nach rechts unten".
  Also ungefähr so:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
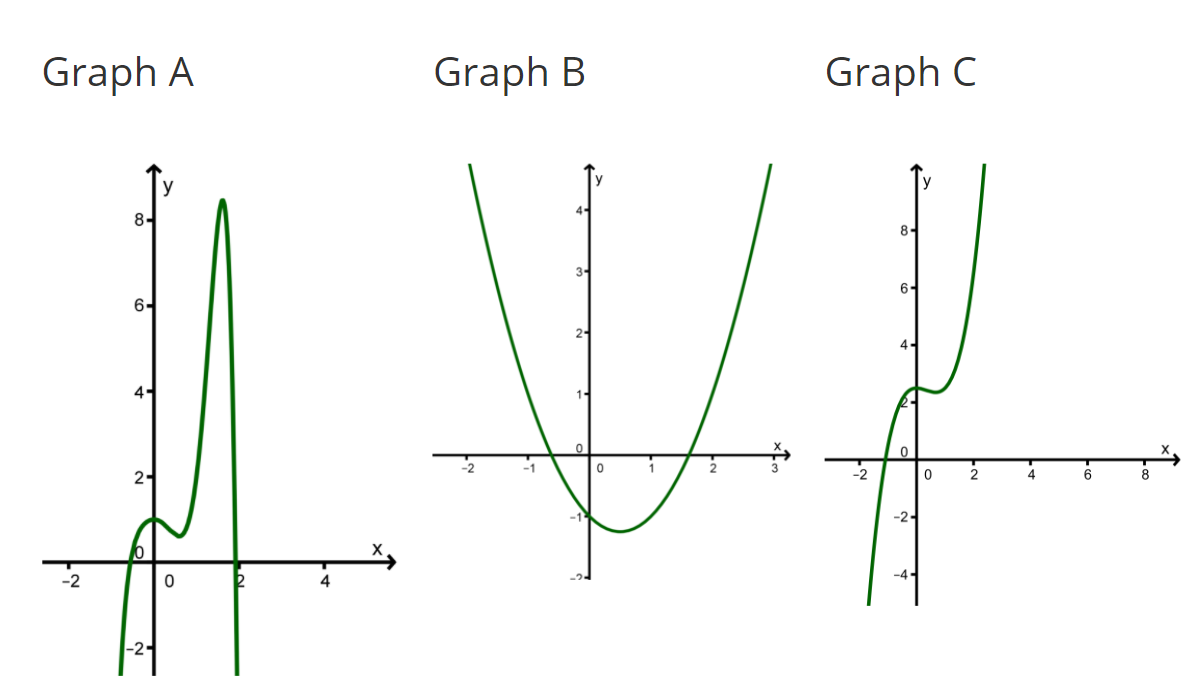
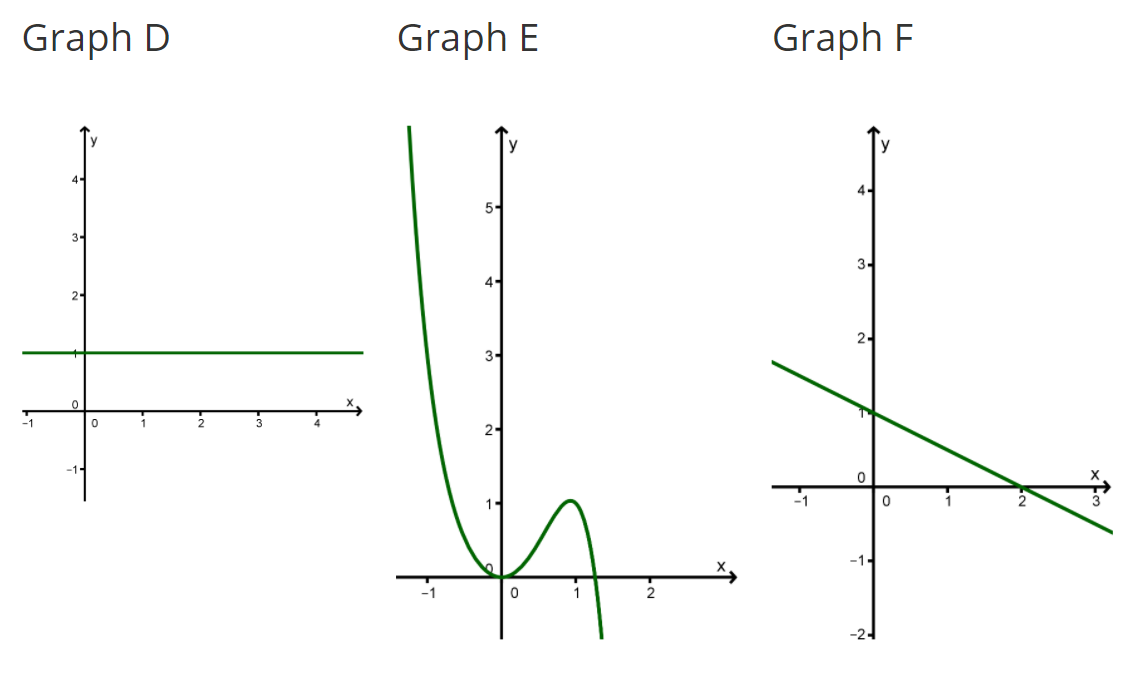
Ordne die Graphen den richtigen Funktionen zu und gib jeweils eine kurze Begründung an. Zu zwei Funktionen gibt es keinen Graphen.
$f(x) = -0.5x+1$
$g(x) = -2x^2$
$h(x) = x^2-x-1$
$i(x) = -3x^6 + 6x^5 -2x^2 +1$
$k(x) = x^3 - x^2 + 2.5$
$l(x) = 1$
$m(x) = -x^5 + 2x^2$
$n(x) = x^6 + x^4$
Für diese Aufgabe benötigst Du folgendes Grundwissen: ganzrationale Funktionen
Eine ganzrationale Funktion ist eine Funktion, die sich aus Polynomen zusammensetzt.
Graph A
Graph A verläuft von links unten nach rechts unten.
Also muss
der höchste Exponent der zugehörigen Polynomfunktion gerade
und der zugehörige Koeffizient negativ sein.
In Frage kommen daher
Funktion $g$ mit $g(x) = -2x^2$ und
Funktion $i$ mit $i(x) = -3x^6 + 6x^5 -2x^2 +1$ .
Funktion $g$ scheidet aus, da ihr Graph eine Parabel sein müsste.
$\Rightarrow$ Ergebnis: Graph A gehört zur Funktion $i$ .
Graph B
Graph B verläuft von links oben nach rechts oben.
Also muss
der höchste Exponent der zugehörigen Polynomfunktion gerade
und der zugehörige Koeffizient positiv sein.
In Frage kommen daher:
Funktion $h$ mit $h(x) = x^2-x-1$ und
Funktion $n$ mit $n(x) = x^6 + x^4$ .
Um zwischen $h$ und $n$ zu unterscheiden, musst du also noch eine weitere Eigenschaft betrachten:
Der Graph von Funktion $n$ wird achsensymmetrisch zur y-Achse sein (Der Funktionsterm von $n$ enthält nur gerade Potenzen von $x$ und damit ist $f(-x)=f(x)$ ).
Der Graph von Funktion $h$ wird keine Symmetrie zur y-Achse aufweisen.
Graph B ist nicht achsensymmetrisch zur y-Achse.
Daher
kommt Funktion $n$ nicht in Frage.
$\Rightarrow$ Ergebnis: Graph B gehört zur Funktion $h$ .
Graph C
Graph C verläuft von links unten nach rechts oben.
Also muss
der höchste Exponent der zugehörigen Polynomfunktion ungerade
und der zugehörige Koeffizient positiv sein.
In Frage kommt daher nur:
Funktion $k$ mit $k(x) = x^3 - x^2 + 2.5$
$\Rightarrow$ Ergebnis: Graph C gehört zur Funktion $k$ .
Graph D
Graph D gehört zu einer konstanten Funktion.
In Frage kommt daher nur:
Funktion $l$ mit $l(x) =1$
$\Rightarrow$ Ergebnis: Graph D gehört zur Funktion $l$ .
Graph E
Graph E verläuft von links oben nach rechts unten.
Also muss
der höchste Exponent der zugehörigen Polynomfunktion ungerade
und der zugehörige Koeffizient negativ sein.
In Frage kommen daher:
Funktion $f$ mit $f(x) = -0.5x+1$ und
Funktion $m$ mit $m(x) = -x^5 + 2x^2$ .
Funktion $f$ scheidet aber aus, da sie eine lineare Funktion ist und deshalb ihr Graph eine Gerade sein müsste.
$\Rightarrow$ Ergebnis: Graph E gehört zur Funktion $m$ .
Graph F
Graph F verläuft von links oben nach rechts unten.
Also muss
der höchste Exponent der zugehörigen Polynomfunktion ungerade
und der zugehörige Koeffizient negativ sein.
In Frage kämen daher wieder $f$ und $m$ . Aber du erkennst leicht:
Graph F ist eine Gerade.
Also muss die zu Graph F gehörende Funktion linear sein; das heißt, dass ihre Funktionsgleichung die Form $y=mx+t$ haben muss.
In Frage kommt daher nur:
Funktion $f$ mit $f(x) = -0.5x+1$
$\Rightarrow$ Ergebnis: Graph F gehört zur Funktion $f$ .
Zusammenfassung:
Graph A: $i$ Graph B: $h$ Graph C: $k$ Graph D: $l$ Graph E: $m$ Graph F: $f$
keinen passenden Graphen: $g$ und $n$
3
Welcher Funktionsterm gehört zum Graph?
2. $f(x)=-x^4$
3. $f(x)=x^5+\frac12x^4-2x$
  $f(x)=-x^3+2x^2$
  $f(x)=2x^4+3x^2+4$
  $f(x)=-3x$
4
Untersuche den Graphen $G_f$ der Funktion $f$ mit $f(x) = -3x^4-2x^2+5$ soweit, sodass du ihn zeichnen kannst.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Ohne Wertetabelle ist es immer geschickt, sich über den Verlauf des Graphens Gedanken zu machen. Hilfreich hierbei sind vor allem erst einmal Nullstellen. Danach schaust du dir das Verhalten der Funktion im Unendlichen an.Um die Nullstellen herauszufinden gibt es zwei Möglichkeiten. Einmal kann man sie bei Polynomen mit einem Grad größer als zwei mit der Polynomdivision herausfinden oder bei dem Grad vier bietet sich auch die Substitution an.
Lösung 1: mit Polynomdivision
1. Schritt: Nullstellen raten
Schaue dir beim raten von Nullstellen die letzte Ziffer ohne ein $x$ an, wie kannst du die $5$ in ein Produkt aufteilen? Zum Beispiel in $1$ und $5$ . Probiere es mit $1$ : Super, eine Nullstelle gefunden!
2. Schritt: Polynomdivision um weitere Nullstellen zu finden
Jetzt sollte man die Wurzel ziehen um auf das $x$ zu kommen. Dann würde aber etwas negatives unter der Wurzel stehen, dies ist nicht erlaubt. Also gibt es keine weitere Nullstelle.
3. Schritt: Verhalten im Unendlichen
Setze jetzt überall da wo in der Funktion ein $x$ steht ein $\infty$ bzw. $-\infty$ ein und schaue was raus kommt. Allerdings darfst du das nur in Anführungszeichen schreiben, da dies eigentlich keine mathematische Ausdrucksweise ist und somit nur eine inoffizielle Lösung aber eine gute Hilfe um sich das besser vorstellen zu können.
Schaue dir jetzt das Vorzeichen vor dem höchsten Exponenten/Grad an: hier steht ein Minus. Also kommt insgesamt Minus Unendlich raus.
Bei geraden Exponenten wird das Minus in der Klammer wieder zu einem Plus und du kommst auf das selbe Ergebnis.
Der Verlauf ist also "von unten nach unten".
4. Schritt: Symmetrie
Es können drei Fälle eintreten: Achsensymmetrie, Punktsymmetrie, keine Symmetrie. Ersetze dafür jedes $x$ mit einem $-x$ .
Jetzt musst du dir die Exponenten/Potenzen anschauen, hier sind das nur gerade, also fallen unsere Minuszeichen vor den $x$ weg. Damit bist du wieder bei der Funktion gelandet.
Welche Symmetrie war das? Richtig, die Achsensymmetrie.
5. Schritt: y-Achsen Abschnitt
Um den Schnittpunkt einer Funktion mit der y-Achse zu ermitteln, muss für den $x$ -Wert $0$ eingesetzt werden.
6. Schritt: Graphen zeichnen
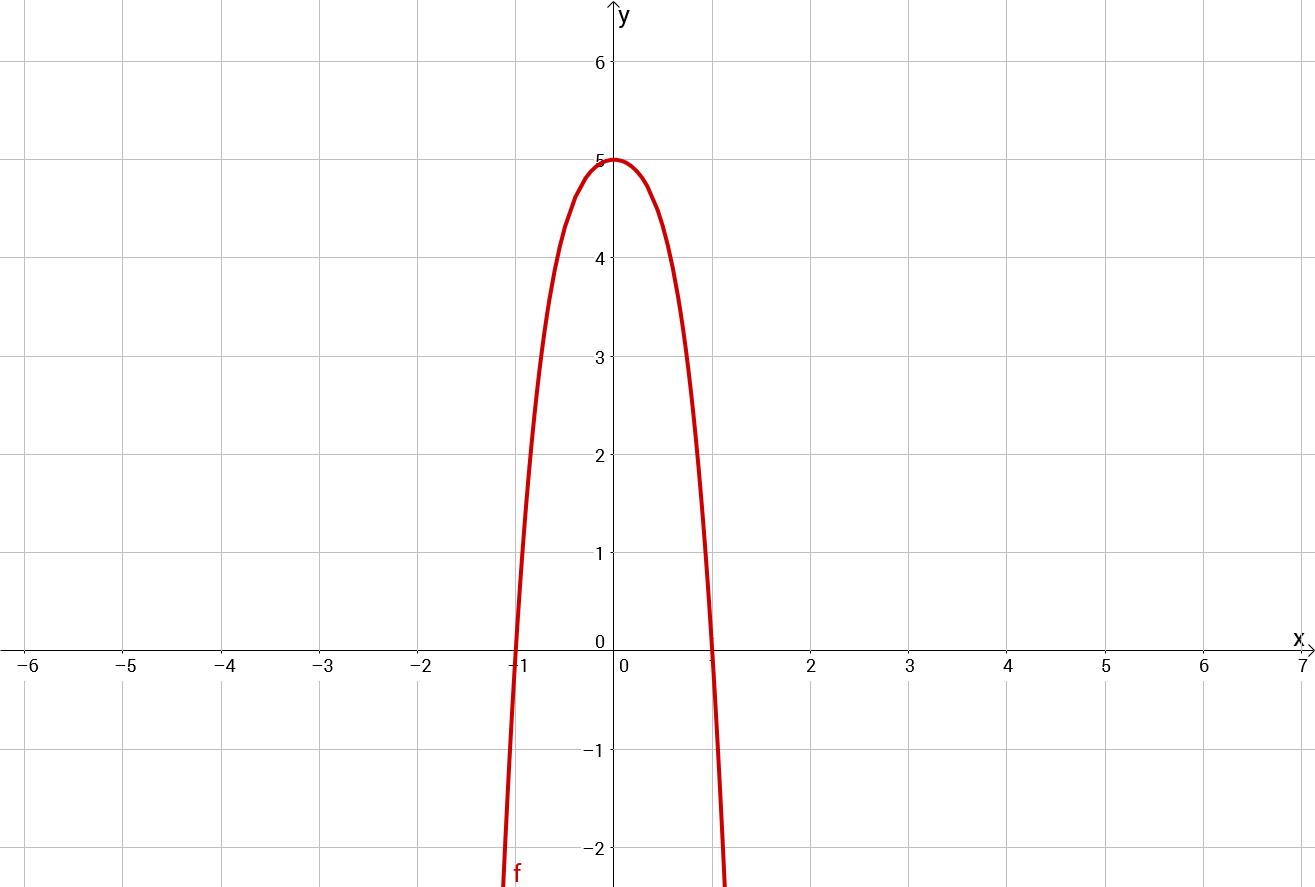
Lösung 2: durch Substitution
Bei der Substitution wird in einem Term ein Teil (z.B. $x^2$ ) durch einen neuen Term (z.B. $z$ ) ersetzt.
Ersetze nun jedes $x^2$ mit $z$ .
Aus dieser quadratischen Funktion kannst du jetzt die Nullstellen mit Hilfe der Mitternachtsformel ausrechnen.
$z_1=-\frac{5}{3}$ und $z_2=1$
Nun musst du rücksubstituieren.
Um auf $x_1$ und $x_2$ zu kommen musst du also die Wurzel aus $z_1$ und $z_2$ ziehen. Das funktioniert allerdings nur bei $z_2$ , da $z_1$ negativ ist. Aber Achtung: Nur die Wurzel ziehen ist keine Äquivalenzumformung, deshalb musst du die $\pm\sqrt{z}$ ziehen.
So bist du wieder bei den Nullstellen von oben angekommen und kannst bei Schritt 3: Verhalten im Unendlichen weiter machen.
Überlege dir, was du alles benötigst, um den Graphen zeichnen zu können:
Nullstellen
Verhalten im Unendlichen
Symmetrie
y-Achsen Abschnitt
5
Skizziere den Graphen $G_f$ der Funktion $f$ mit $f(x)=-3x^4+2x^2+5$ nur durch Überlegung und ohne Wertetabelle.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomfunktion
Zuerst wird die Funktion in die einzelnen Terme aufgeteilt.

Betrachte $-3x^4$ . Das Vorzeichen sagt dir, dass eine nach unten geöffnete Polynomfunktion vierten Grades vorliegt. Diese ist durch den Faktor 3 relativ schmal. Da hier der höchste Exponent der Funktion vorliegt, sieht die Funktion nach außen betrachtet aus, wie eine Funktion vierten Grades.
Betrachte $+2x^2$ . Das Vorzeichen sagt dir, dass eine nach oben geöffnete Parabel vorliegt, die durch den Faktor 2 ebenfalls etwas schmaler wird. Da hier der kleinste Exponent vorliegt, sieht die Funktion bei kleinen x-Werten, also in der Umgebung von Null, so aus wie eine Parabel.
Betrachte $+5$ .
Hier liegt keine Verknüpfung mit einem $x$ vor, deswegen ist die 5 die Verschiebung auf der y-Achse, und zwar in die positive Richtung.
Es liegen also nur gerade Exponenten vor. Dies sagt dir, dass der Graph symmetrisch ist.
Die Terme wieder zusammen in der Funktion ergibt dann das:
Überlege dir zuerst, was die Vorzeichen für Auswirkungen auf die Funktion haben. Wo hast du Potenzen, welchen Grad haben diese? Welcher y-Achsen-Abschnitt liegt vor?

Bestimme bei folgenden Funktionen den Definitionsbereich, die Nullstellen, das Symmetrieverhalten, die Grenzwerte und die Wertemenge.

$f(x)=-x^4-2x^2+3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion

Definitionsbereich festlegen

Der Definitionsbereich gibt an, welche $x$ -Werte in eine Funktion eingesetzt werden dürfen.

Da die Funktion keine Brüche , Wurzeln oder Logarithmen mit $x$ enthält, die den Definitionsbereich einschränken könnten, lautet der Definitionsbereich der Funktion $D_f=ℝ$ .

Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

Substitution

Bei der Substitution wird in einem Term ein Teil (z.B. $x^2$ ) durch einen neuen Term (z.B. $u$ ) ersetzt.

$\displaystyle f\left(x\right)$	$=$	$\displaystyle -x^4-2x^2+3$
	↓	In $f(x)$ wird $x^2$ durch $u$ ersetzt, wodurch man die Funktion $f(u)$ erhält.
$\displaystyle f\left(u\right)$	$=$	$\displaystyle -u^2-2u+3$
	↓	Mitternachtsformel anwenden.
$\displaystyle u_{1{,}2}$	$=$	$\displaystyle \frac{2\pm\sqrt{\left(-2\right)^2-4\cdot\left(-1\right)\cdot3}}{2\cdot\left(-1\right)}$
	↓	Unter der Wurzel zusammenfassen.
	$=$	$\displaystyle \frac{2\pm\sqrt{4+12}}{-2}$
	↓	Unter der Wurzel addieren.
	$=$	$\displaystyle \frac{2\pm\sqrt{16}}{-2}$
	$=$	$\displaystyle \frac{2\pm4}{-2}$
$\displaystyle u_1$	$=$	$\displaystyle -3$	$\displaystyle Fall\ 1:+$
$\displaystyle u_2$	$=$	$\displaystyle 1$	$\displaystyle Fall\ 2:-$

Resubstitution

Die Resubstitution beschreibt das Rückgängigmachen der Substitution.

$x_{1{,}2}^2=u_1=-3$

Radizieren.

Für $\sqrt{-3}$ gibt es keine reelle Lösung.

$x_{3{,}4}^2=u_2=1$

Wurzel ziehen.

$x_{3{,}4}=\pm1$

Da es für $x_{1{,}2}$ keine reelle Lösung gibt, sind $x_{3{,}4}$ die einzigen Nullstellen von $f(x)$ .

Die Funktion $f(x)$ hat zwei Nullstellen bei $x_3=-1$ , $x_4=1$ .

Symmetrieverhalten

In dieser Lösung wird die Symmetrie der Funktion durch einfache Betrachtung und durch Berechnung überprüft.

Durch Betrachtung

Alle Exponenten zur Basis $x$ sind gerade.

$\Rightarrow$ Achsensymmetrie bezüglich der $y$ -Achse.

Durch Berechnung

$\displaystyle f\left(x\right)$	$=$	$\displaystyle -x^4-2x^2+3$
	↓	Prüfen ob $f(x)=f(-x)$ . Setze dafür $-x$ in $f(x)$ ein.
$\displaystyle f\left(-x\right)$	$=$	$\displaystyle -\left(-x\right)^4-2\left(-x\right)^2+3$
	↓	Umformen.
$\displaystyle f\left(x\right)$	$=$	$\displaystyle -x^4-2x^2+3$

$\Rightarrow$ Achsensymmetrie zur $y$ -Achse

Grenzwertbetrachtung

Bei der Grenzwertbetrachtung wird das Verhalten einer Funktion und ihres Graphen im Unendlichen oder an einer bestimmten Stelle (meist Definitionslücke) ermittelt.

$D_f=ℝ$

Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm\infty$ betrachtet werden.

Bei ganzrationalen Funktionen ist nur die höchste Potenz wichtig, um die Grenzwertbetrachtung durchzuführen.

gegen $+\infty$

$\displaystyle\lim_{x\rightarrow\infty}\overset{\overset{\rightarrow-\infty}︷}{-x^4}-\overset{\overset{\rightarrow\infty}︷}{2x^2}+3=-\infty$

gegen $-\infty$

$\displaystyle\lim_{x\rightarrow-\infty}\overset{\overset{\rightarrow-\infty}︷}{-x^4}-\overset{\overset{\rightarrow\infty}︷}{2x^2}+3=-\infty$

Wertemenge bestimmen

Die Wertemenge einer Funktion ist die Menge aller möglichen Funktionswerte, die herauskommen können, wenn man alle Zahlen aus der Definitionsmenge in die Funktion einsetzt.

Anhand der Grenzwerte kannst du erkennen, dass der Graph der Funktion eine nach unten geöffnete Parabel ist. Somit beschreibt der Scheitelpunkt den höchsten Punkt des Graphen. Da die Funktion achsensymmetrisch ist, liegt die $x$ -Koordinate des Scheitelpunkts zwischen den Nullstellen, also bei $x=0$ .

Der Scheitelpunkt liegt also bei $S(0|f(0))$ .

Berechne $f(0)$ .

$f(0)=-0^4-2\cdot0^2+3=3$

Gib die Wertemenge an.

$\mathbb {W_f}=]-\infty; 3]$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$g(x)=x^2+2x+1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion

Definitionsbereich festlegen

Der Definitionsbereich gibt an, welche $x$ -Werte in eine Funktion eingesetzt werden dürfen.

Da die Funktion keine Brüche , Wurzeln oder Logarithmen mit $x$ enthält, die den Definitionsbereich einschränken könnten, lautet der Definitionsbereich der Funktion $D_g=ℝ$ .

Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

$\displaystyle g\left(x\right)$	$=$	$\displaystyle x^2+2x+1$
	↓	Setze $g(x)=0$ .
$\displaystyle x^2+2x+1$	$=$	$\displaystyle 0$
	↓	1. Binomische Formel anwenden.
$\displaystyle \left(x+1\right)^2$	$=$	$\displaystyle 0$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle -1$

Die Funktion $g(x)$ hat eine doppelte Nullstelle bei $x_{1{,}2}=-1$ .

Symmetrieverhalten

In dieser Lösung wird die Symmetrie der Funktion durch einfache Betrachtung und durch Berechnung überprüft.

Durch Betrachtung

Da nicht alle Exponenten zur Basis $x$ gerade sind, ist $g$ nicht achsensymmetrisch bezüglich zur $y$ -Achse.

Da nicht alle Exponenten zur Basis $x$ ungerade sind, ist $g$ nicht punktsymmetrisch zum Ursprung.

Somit besitzt $g$ also keine Symmetrie bezüglich der $y$ -Achse oder des Ursprungs.

Durch Berechnung

$g(x)=x^2+2x+1$

Prüfen ob $g(x)=g(-x)$ . Setze dafür $-x$ in $g(x)$ ein.

$g(-x)=(-x)^2+2\cdot(-x)+1$

$\phantom{g(-x)}=x^2-2x+1\neq g(x)$

$\Rightarrow$ keine Achsensymmetrie zur $y$ -Achse

Prüfen ob $g(x)=-g(-x)$ .

$-g(-x)=-(x^2-2x+1)=-x^2+2x-1\neq g(x)$

$\Rightarrow$ keine Punktymmetrie zum Ursprung

Somit liegt bei $g$ keine Symmetrie bezüglich der $y$ -Achse oder des Ursprungs vor.

Grenzwertbetrachtung

Bei der Grenzwertbetrachtung wird das Verhalten einer Funktion und ihres Graphen im Unendlichen oder an einer bestimmten Stelle (meist Definitionslücke) ermittelt.

$D_g=ℝ$

Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm\infty$ betrachtet werden.

Bei ganzrationalen Funktionen ist nur die höchste Potenz wichtig, um die Grenzwertbetrachtung durchzuführen.

gegen $+\infty$

$\displaystyle\lim_{x\rightarrow\infty}\overset{\overset{\rightarrow\infty}︷}{x^2}+\overset{\overset{\rightarrow\infty}︷}{2x}+1=\infty$

gegen $-\infty$

$\displaystyle\lim_{x\rightarrow-\infty}\overset{\overset{\rightarrow\infty}︷}{x^2}+\overset{\overset{\rightarrow-\infty}︷}{2x}+1=\infty$

Wertemenge bestimmen

Die Wertemenge einer Funktion ist die Menge aller möglichen Funktionswerte, die herauskommen können, wenn man alle Zahlen aus der Definitionsmenge in die Funktion einsetzt.

Anhand der Grenzwerte kannst du erkennen, dass der Graph der Funktion eine nach oben geöffnete Parabel ist. Somit beschreibt der Scheitelpunkt den tiefsten Punkt des Graphen. Da die Funktion eine doppelte Nullstelle bei $x_{1{,}2}=-1$ besitzt, ist die Nullstelle zugleich der Scheitelpunkt.

Der Scheitelpunkt liegt also bei $S(-1|0)$ .

Gib die Wertemenge an.

$\mathbb {W_f}=[0; \infty[$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$h(x)=-x^3+4x$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion

Definitionsbereich festlegen

Der Definitionsbereich gibt an, welche $x$ -Werte in eine Funktion eingesetzt werden dürfen.

Da die Funktion keine Brüche , Wurzeln oder Logarithmen mit $x$ enthält, die den Definitionsbereich einschränken könnten, lautet der Definitionsbereich der Funktion $D_h=ℝ$ .

Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

Ausklammern

Um diese Aufgabe lösen zu können, brauchst du Wissen über das Ausklammern.

$\displaystyle h\left(x\right)$	$=$	$\displaystyle -x^3+4x$
	↓	Klammere $x$ aus (kleinster vorkommender Exponent von $x$ ).
$\displaystyle h\left(x\right)$	$=$	$\displaystyle x\cdot\left(-x^2+4\right)$
	↓	Setze $h(x)=0$ .
$\displaystyle 0$	$=$	$\displaystyle x\left(-x^2+4\right)$
	↓	Ein Produkt ist immer dann null, wenn einer seiner Faktoren null ist!

$\Rightarrow x_1=0$

Setze die Klammer gleich Null und löse nach $x$ auf.

$\def\arraystretch{1.25} \begin{array}{rcl}-x^2+4&=&0&|+x^2\\4&=&x^2&|\sqrt{}\\\pm2&=&x_{2{,}3}\end{array}$

Die Funktion $h(x)$ hat drei Nullstellen bei $x_1=0$ , $x_2=-2$ und $x_3=2$ .

Symmetrieverhalten

In dieser Lösung wird die Symmetrie der Funktion durch einfache Betrachtung und durch Berechnung überprüft.

Durch Betrachtung

Alle Exponenten von $x$ sind ungerade.

$\Rightarrow$ Punktsymmetrie bezüglich des Ursprungs.

Durch Berechnung

$h(x)=-x^3+4x$

Prüfen ob $h(x)=h(-x)$ . Setze dafür $-x$ in $h(x)$ ein.

$h(-x)=-(-x)^3+4\cdot(-x)$

$\phantom{h(-x)}=x^3-4x\neq h(x)$

$\Rightarrow$ keine Achsensymmetrie zur $y$ -Achse

Prüfen ob $h(x)=-h(-x)$ .

$\displaystyle -h\left(-x\right)$	$=$	$\displaystyle -\left(x^3-4x\right)$
$\displaystyle h\left(x\right)$	$=$	$\displaystyle -x^3+4x$

$\Rightarrow$ Punktymmetrie bezügöich des Ursprungs

Grenzwertbetrachtung

Bei der Grenzwertbetrachtung wird das Verhalten einer Funktion und ihres Graphen im Unendlichen oder an einer bestimmten Stelle (meist Definitionslücke) ermittelt.

$D_h=ℝ$

Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm\infty$ betrachtet werden.

gegen $+\infty$

$\displaystyle\lim_{x\rightarrow\infty}\overset{\overset{\rightarrow-\infty}︷}{-x^3}+\overset{\overset{\rightarrow\infty}︷}{4x}=-\infty$

gegen $-\infty$

$\displaystyle\lim_{x\rightarrow-\infty}\overset{\overset{\rightarrow\infty}︷}{-x^3}+\overset{\overset{\rightarrow-\infty}︷}{4x}=\infty$

Wertemenge bestimmen

Die Wertemenge einer Funktion ist die Menge aller möglichen Funktionswerte, die herauskommen können, wenn man alle Zahlen aus der Definitionsmenge in die Funktion einsetzt.

Da es sich um eine ganzrationale Funktion 3. Grades handelt, wird der Wertebereich nicht eingeschränkt. Somit lautet die Wertemenge:

$\mathbb {W_f}=\mathbb{R}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$i(x)=x^3-4x^2-3x+18$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion

Definitionsbereich festlegen

Der Definitionsbereich gibt an, welche $x$ -Werte in eine Funktion eingesetzt werden dürfen.

Da die Funktion keine Brüche , Wurzeln oder Logarithmen mit $x$ enthält, die den Definitionsbereich einschränken könnten, lautet der Definitionsbereich der Funktion $D_i=ℝ$ .

Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

$\displaystyle i\left(x\right)$	$=$	$\displaystyle x^3-4x^2-3x+18$
	↓	Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $-2$ in $i(x)$ ein.
$\displaystyle i\left(-2\right)$	$=$	$\displaystyle \left(-2\right)^3-4\cdot\left(-2\right)^2-3\cdot\left(-2\right)+18$
$\displaystyle 0$	$=$	$\displaystyle -8-16+6+18$

Die Funktion $i(x)$ hat an der Stelle $x_1=-2$ eine Nullstelle. Da $i(-2)=0$ , wissen wir, dass $i(x)$ den dazugehörigen Linearfaktor $(x+2)$ besitzt.

Führe nun die Polynomdivision $i(x):(x+2)$ durch.

$\def\arraystretch{1.25} \begin{array}{l}{-}(x^3-4x^2-3x+18):(x+2)=x^2-6x+9\\\underline{-(x^3+2x^2)\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;-6x^2-3x\\\;\;\;\;\;\;\underline{-(-6x^2-12x)\;\;\;\;}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;9x+18\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(9x+18)}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$

Die Funktion $g(x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_1=-2$ bereits bekannt ist, kannst du die weiteren Nullstellen von $i$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.

$\displaystyle x^2-6x+9$	$=$	$\displaystyle 0$
	↓	2. Binomische Formel anwenden.
$\displaystyle \left(x-3\right)^2$	$=$	$\displaystyle 0$
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle 3$

Die Funktion $i(x)$ hat eine einfache Nullstelle bei $x_1=-2$ und eine doppelte Nullstelle bei $x_{2{,}3}=3$ .

Symmetrieverhalten

In dieser Lösung wird die Symmetrie der Funktion durch einfache Betrachtung und durch Berechnung überprüft.

Durch Betrachtung

Da nicht alle Exponenten zur Basis $x$ gerade sind, ist $i$ nicht achsensymmetrisch bezüglich zur $y$ -Achse.

Da nicht alle Exponenten zur Basis $x$ ungerade sind, ist $i$ nicht punktsymmetrisch zum Ursprung.

Somit besitzt $i$ also keine Symmetrie bezüglich der $y$ -Achse oder des Ursprungs.

Durch Berechnung

$\displaystyle i\left(x\right)$	$=$	$\displaystyle x^3-4x^2-3x+18$
	↓	Prüfen ob $i(x)=i(-x)$ . Setze dafür $-x$ in $i(x)$ ein.
$\displaystyle i\left(-x\right)$	$=$	$\displaystyle \left(-x\right)^3-4\cdot\left(-x\right)^2-3\cdot\left(-x\right)+18$

$\phantom{i(-x)}=-x^3-4x^2+3x+18\neq i(x)$

$\Rightarrow$ keine Achsensymmetrie zur $y$ -Achse

Prüfen ob $i(x)=-i(-x)$ .

$-i(-x)=-(-x^3-4x^2+3x+18)$

$\phantom{-i(-x)}=x^3+4x^2-3x-18\neq i(x)$

$\Rightarrow$ keine Punktymmetrie zum Ursprung

Somit liegt bei $i$ keine Symmetrie bezüglich der $y$ -Achse oder des Ursprungs vor.

Grenzwertbetrachtung

Bei der Grenzwertbetrachtung wird das Verhalten einer Funktion und ihres Graphen im Unendlichen oder an einer bestimmten Stelle (meist Definitionslücke) ermittelt.

$D_i=ℝ$

Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm\infty$ betrachtet werden.

Bei ganzrationalen Funktionen ist nur die höchste Potenz wichtig, um die Grenzwertbetrachtung durchzuführen.

gegen $+\infty$

$\displaystyle\lim_{x\rightarrow\infty}\overset{\overset{\rightarrow\infty}︷}{x^3}-\overset{\overset{\rightarrow\infty}︷}{4x^2}-\overset{\overset{\rightarrow\infty}︷}{3x}+18=\infty$

gegen $-\infty$

$\displaystyle\lim_{x\rightarrow-\infty}\overset{\overset{\rightarrow-\infty}︷}{x^3}-\overset{\overset{\rightarrow\infty}︷}{4x^2}-\overset{\overset{\rightarrow-\infty}︷}{3x}+18=-\infty$

Wertemenge bestimmen

Die Wertemenge einer Funktion ist die Menge aller möglichen Funktionswerte, die herauskommen können, wenn man alle Zahlen aus der Definitionsmenge in die Funktion einsetzt.

Da es sich um eine ganzrationale Funktion 3. Grades handelt, wird der Wertebereich nicht eingeschränkt. Somit lautet die Wertemenge:

$\mathbb {W_f}=\mathbb{R}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zu Polynomfunktionen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Erste Variante:

Zweite Variante (etwas fortgeschrittener):

Hast du eine Frage oder Feedback?

Was solltest Du über (1−x2)2(1-x^2)^2(1−x2)2 zu wissen?

Weiter geht's mit hhh

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Graph A

Graph B

Graph C

Graph D

Graph E

Graph F

Zusammenfassung:

Lösung 1: mit Polynomdivision

1. Schritt: Nullstellen raten

2. Schritt: Polynomdivision um weitere Nullstellen zu finden

3. Schritt: Verhalten im Unendlichen

4. Schritt: Symmetrie

5. Schritt: y-Achsen Abschnitt

6. Schritt: Graphen zeichnen

Lösung 2: durch Substitution

Definitionsbereich festlegen

Nullstellenbestimmung

Substitution

Resubstitution

Symmetrieverhalten

Durch Betrachtung

Durch Berechnung

Grenzwertbetrachtung

gegen +∞+\infty+∞

gegen −∞-\infty−∞

Wertemenge bestimmen

Hast du eine Frage oder Feedback?

Definitionsbereich festlegen

Nullstellenbestimmung

Symmetrieverhalten

Durch Betrachtung

Durch Berechnung

Grenzwertbetrachtung

gegen +∞+\infty+∞

gegen −∞-\infty−∞

Wertemenge bestimmen

Hast du eine Frage oder Feedback?

Definitionsbereich festlegen

Nullstellenbestimmung

Ausklammern

Symmetrieverhalten

Durch Betrachtung

Durch Berechnung

Grenzwertbetrachtung

gegen +∞+\infty+∞

gegen −∞-\infty−∞

Wertemenge bestimmen

Hast du eine Frage oder Feedback?

Definitionsbereich festlegen

Nullstellenbestimmung

Symmetrieverhalten

Durch Betrachtung

Durch Berechnung

Grenzwertbetrachtung

gegen +∞+\infty+∞

gegen −∞-\infty−∞

Wertemenge bestimmen

Hast du eine Frage oder Feedback?

Was solltest Du über $(1-x^2)^2$ zu wissen?

Weiter geht's mit $h$

gegen $+\infty$

gegen $-\infty$

gegen $+\infty$

gegen $-\infty$

gegen $+\infty$

gegen $-\infty$

gegen $+\infty$

gegen $-\infty$