1 Übersicht
wird aktuell überarbeitet
Inhalt des Kurses
Dieser Kurs dient der Abiturvorbereitung im Themengebiet Stochastik.
Er gibt einen zusammenfassenden Überblick über die wichtigsten Inhalte der gymnasialen Oberstufe:
Grundlagen der Stochastik
Zufallsgrößen
Urnenmodelle
Binomialverteilung
Beurteilende Statistik
Dabei sind Begriffe und Inhalte aus früheren Klassenstufen entsprechend verlinkt, sodass sie bei Bedarf wiederholt werden können.
Vorkenntnisse
Du solltest die oben genannten Inhalte bereits kennengelernt haben, sodass sie dir zumindest grob vertraut sind.
Außerdem ist es hilfreich, wenn du die Stochastik der Unter- und Mittelstufe einigermaßen beherrschst.
2 Zufallsexperimente
Zufall
Der Begriff des Zufalls ist im Allgemeinen zwar nicht leicht zu fassen für die Mathematik reicht es aber, den Zufall schlicht als etwas Unvorhersagbares anzusehen.
Dementsprechend ist ein Zufallsexperiment ein Experiment mit einem unvorhersagbaren Ausgang.
Dennoch können mithilfe der Mathematik aber Aussagen über das Verhalten bei sehr vielen Wiederholungen eines Zufallsexperiments getroffen werden.
Grundlegende Begriffe
Um den Zufall mathematisch zu modellieren, muss man zunächst festlegen, was das Zufallsexperiment für Ausgänge haben kann.
Einen möglichen Ausgang des Zufallsexperiments nennt man dabei Ergebnis .
Der Ergebnisraum fasst alle möglichen Ergebnisse in einer Menge zusammen, also . Die Mächtigkeit des Ergebnisraumes gibt an, wie viele Ergebnisse in ihm enthalten sind, also .
Mehrere Ergebnisse können zu einem Ereignis zusammengefasst werden; mathematisch ist ein Ereignis somit eine Teilmenge von , also . Das zugehörige Gegenereignis enthält alle Ergebnisse, die nicht in sind, also .
Beispiel
Auf einem Volksfest gibt es ein Glücksrad. Es hat drei gleich große Sektoren in rot (r), gelb (g) oder blau (b). Man darf zweimal hintereinander drehen.
Die möglichen Ergebnisse sind im Ergebnisraum aufgeschrieben .
Das Ereignis "mindestens einmal rot" hat die Ergebnismenge .
Das Gegenereignis dazu ist "kein einziges Mal rot" und hat die Ergebnismenge .
3 Wahrscheinlichkeit
Wie bereits erwähnt, lässt sich der Ausgang eines einzelnen Zufallsexperiments nicht vorhersagen (er ist eben gerade "zufällig"), man kann allerdings eine Tendenz angeben, was passieren wird, wenn man das Zufallsexperiment sehr oft wiederholt.
Denn das empirische Gesetz der großen Zahlen besagt, dass sich mit steigender Anzahl an Durchführungen die relative Häufigkeit eines Ereignisses um einen bestimmten Wert stabilisiert. Diesen theoretischen Wert nennt man Wahrscheinlichkeit und schreibt ihn als .
Die mathematisch-formale Grundlage für den Wahrscheinlichkeitsbegriff bilden die Axiome von Kolmogorow. Sie sind für das Abitur nicht von zentraler Bedeutung, daher befinden sie sich im Spoiler.
Laplace-Experimente
Eine wichtige Art von Zufallsexperiment stellt das Laplace-Experiment dar, bei dem alle Ergebnisse gleich wahrscheinlich sind. Bei einer genügend großen Versuchszahl ist demzufolge zu erwarten, dass alle Ergebnisse im Mittel etwa gleich oft auftreten.
Die Wahrscheinlichkeit eines Ereignisses ergibt sich somit als folgendes Verhältnis:
4 Beispiel zu Zufallsexperimente und Wahrscheinlichkeit
Die eingeführten Begriffe sollen beispielhaft anhand des Werfens eines herkömmlichen Spielwürfels veranschaulicht werden:
Ergebnis : (Würfel zeigt Augenzahl 4)
Ergebnisraum: ,
Diese Festlegung der Ergebnisse und des Ergebnisraumes ist bereits Teil der mathematischen Modellierung, die dem jeweiligen Kontext angemessen erfolgen sollte. So kann unter gewissen Umständen (z. B. beim Wurf auf einem dicken Teppich) auch "Würfel landet auf Kante" ein sinnvolles Ergebnis sein.
Ereignis : Würfel zeigt Augenzahl kleiner als drei,
Gegenereignis : Würfel zeigt Augenzahl größer oder gleich 3,
Sofern es keine triftigen Gründe gibt, die dagegen sprechen, wird der Würfelwurf in der Regel als Laplace-Experiment angenommen. Man geht also von einem fairen (d. h. nicht gezinkten) Würfel aus, bei dem auf lange Sicht alle sechs Seiten in etwa gleich häufig fallen.
Wahrscheinlichkeit:
Bei sehr vielen Würfen ist somit zu erwarten, dass im Mittel etwa jeder dritte Wurf eine Augenzahl kleiner als 3 ergibt.
5 Zusammengesetzte Ereignisse
Auf Basis der Mengenlehre können zwei (oder mehr) Ereignisse auf verschiedene Weisen kombiniert werden.
Wichtige Verknüpfungen sind dabei die "und"-, "oder"- und "ohne"-Verknüpfung:
Der Schnitt - "und" | Die Vereinigung - "oder" | Die Differenz - "ohne" |
|---|---|---|
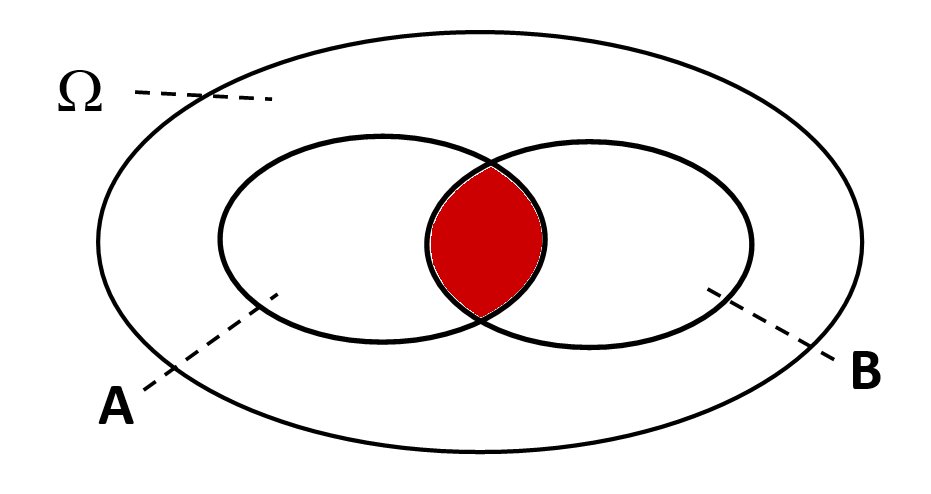 | 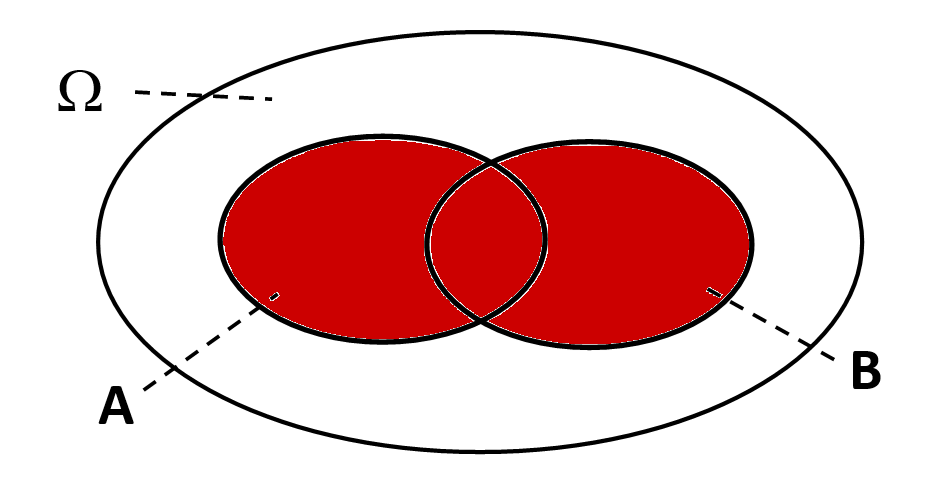 | 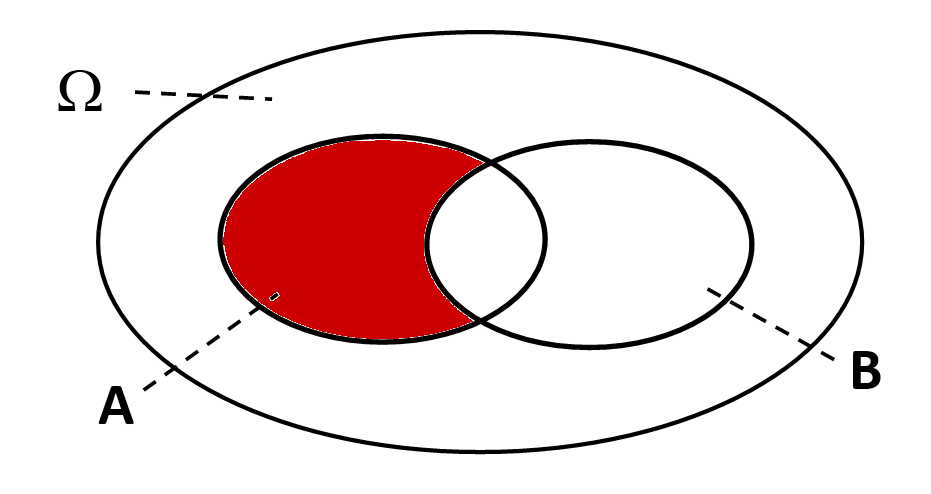 |
" und ": (alle Ergebnisse, die sowohl in als auch in enthalten sind) | " oder ": (alle Ergebnisse, die in oder in oder in beiden enthalten sind) | " ohne ": (alle Ergebnisse, die in , aber nicht in enthalten sind) |
Gesetze von De Morgan
Beim Bilden des Gegenereignisses von zusammengesetzten Ereignissen sind folgende Beziehungen nützlich, die auch Gesetze von De Morgan genannt werden:
Additionssatz
Für zwei beliebige Ereignisse und kann die Wahrscheinlichkeit von mithilfe des Additionssatzes berechnet werden:
6 Unabhängigkeit
In vielen Situationen ist die Frage interessant, ob sich bestimmte Zufallsereignisse gegenseitig beeinflussen. Diese Vorstellung wird mathematisch durch das Konzept der (stochastischen) Unabhängigkeit formalisiert.
Zwei Ereignisse und heißen (stochastisch) unabhängig, wenn das Eintreten von keinen Einfluss auf das Eintreten von hat und umgekehrt.
Mathematisch ausgedrückt:
Dabei ist die bedingte Wahrscheinlichkeit.
Eine äquivalente (also gleichwertige), aber in der Praxis oft nützlichere Charakterisierung der Unabhängigkeit lautet:
Sind die Ereignisse und unabhängig, so sind auch und , und sowie und unabhängig. In diesem Fall ist die zugehörige Vierfeldertafel eine Multiplikationstafel (d. h. die äußeren Einträge ergeben sich durch Multiplikation der inneren).
7 Aufgabe zu Ereignissen und Unabhängigkeit
Laden
8 Zufallsgrößen (1/2)
Um Zufallsexperimente mathematisch besser verstehen und modellieren zu können, ist es hilfreich, das Konzept der Zufallsgröße (bzw. Zufallsvariable) einzuführen.
Darunter versteht man eine Funktion mit und ; d. h. eine Zufallsgröße ordnet jedem Ergebnis eines Zufallsexperiments eine reelle Zahl zu.
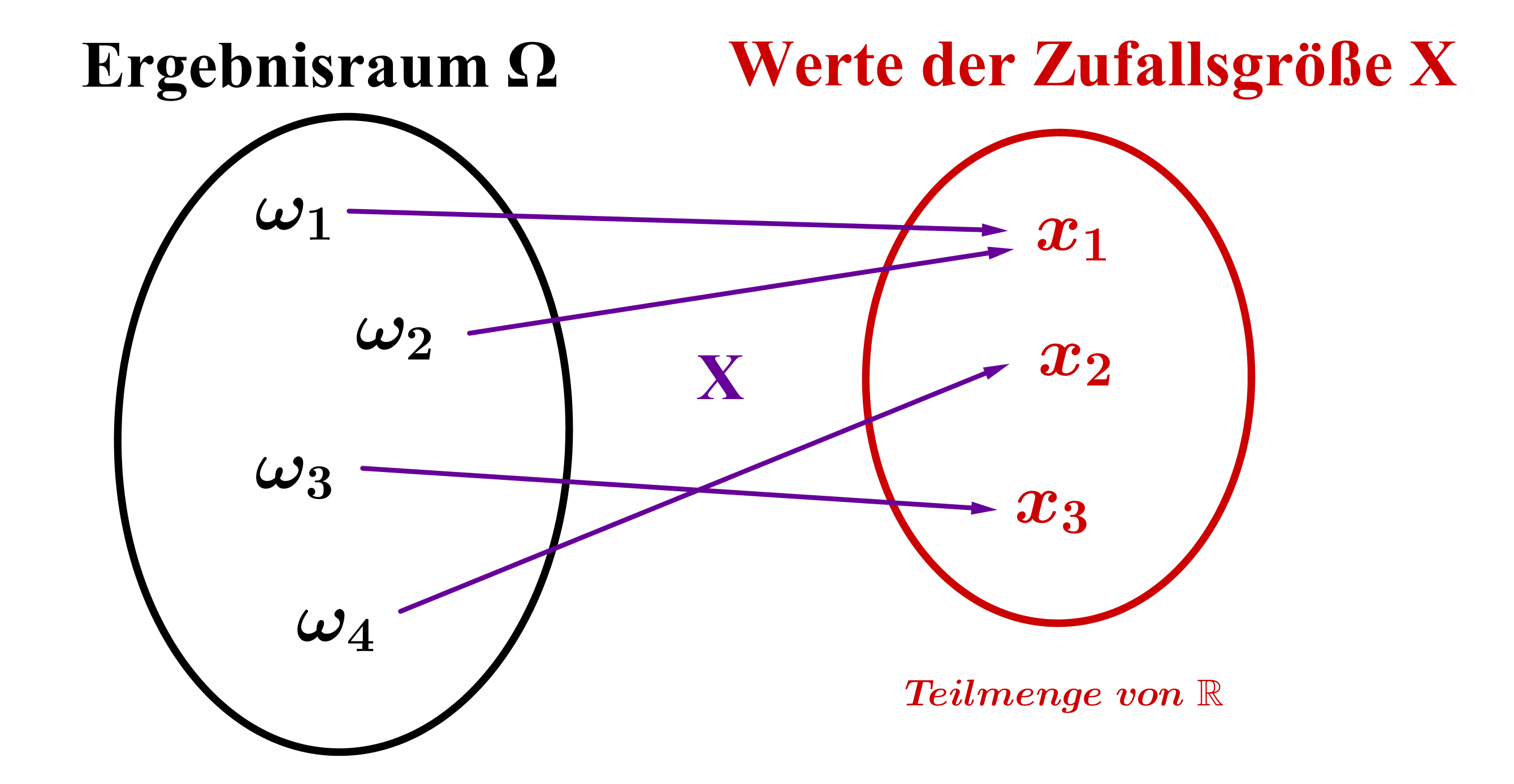
Wahrscheinlichkeiten
Als Verbindung zum Konzept der Wahrscheinlichkeit führt man darauf aufbauend zwei weitere Funktionen ein:
Die Wahrscheinlichkeitsverteilung von ist die Funktion , die jedem Wert der Zufallsgröße seine Wahrscheinlichkeit zuordnet.
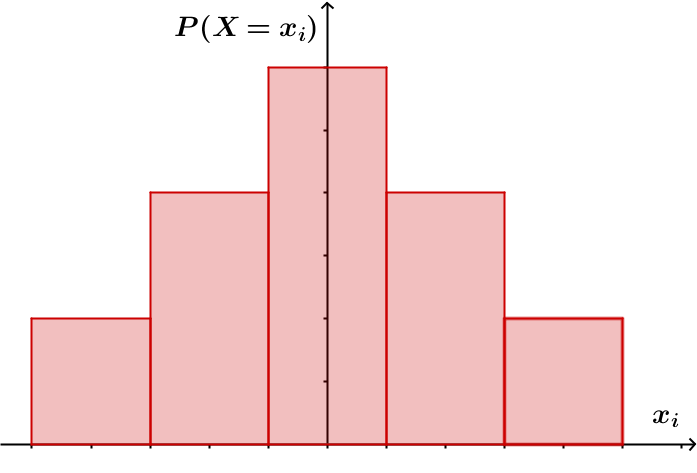
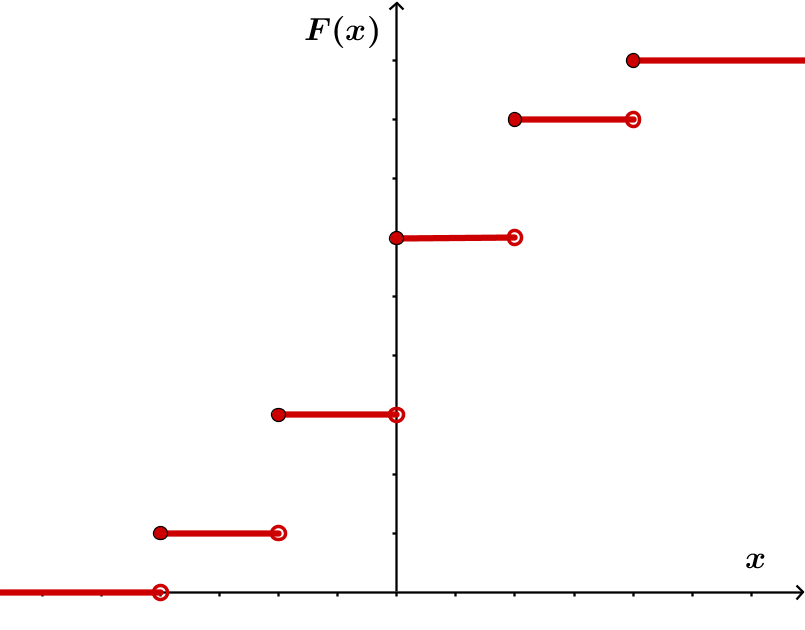
Die kumulative Verteilungsfunktion von ist die Funktion mit , die jeder reellen Zahl die Wahrscheinlichkeit zuordnet, dass die Zufallsgröße einen Wert kleiner oder gleich annimmt.
9 Zufallsgrößen (2/2)
Dieser Umweg über Zufallsgrößen scheint auf den ersten Blick unnötig umständlich zu sein, denn bisher haben wir jedem Ergebnis eines Zufallsexperiments direkt eine Wahrscheinlichkeit zugeordnet (vgl. Spielwürfel-Beispiel: ).
Nun ordnen wir jedem Ergebnis zunächst eine Zahl (den Wert der Zufallsgröße ) und dann dieser Zahl erst eine Wahrscheinlichkeit zu.
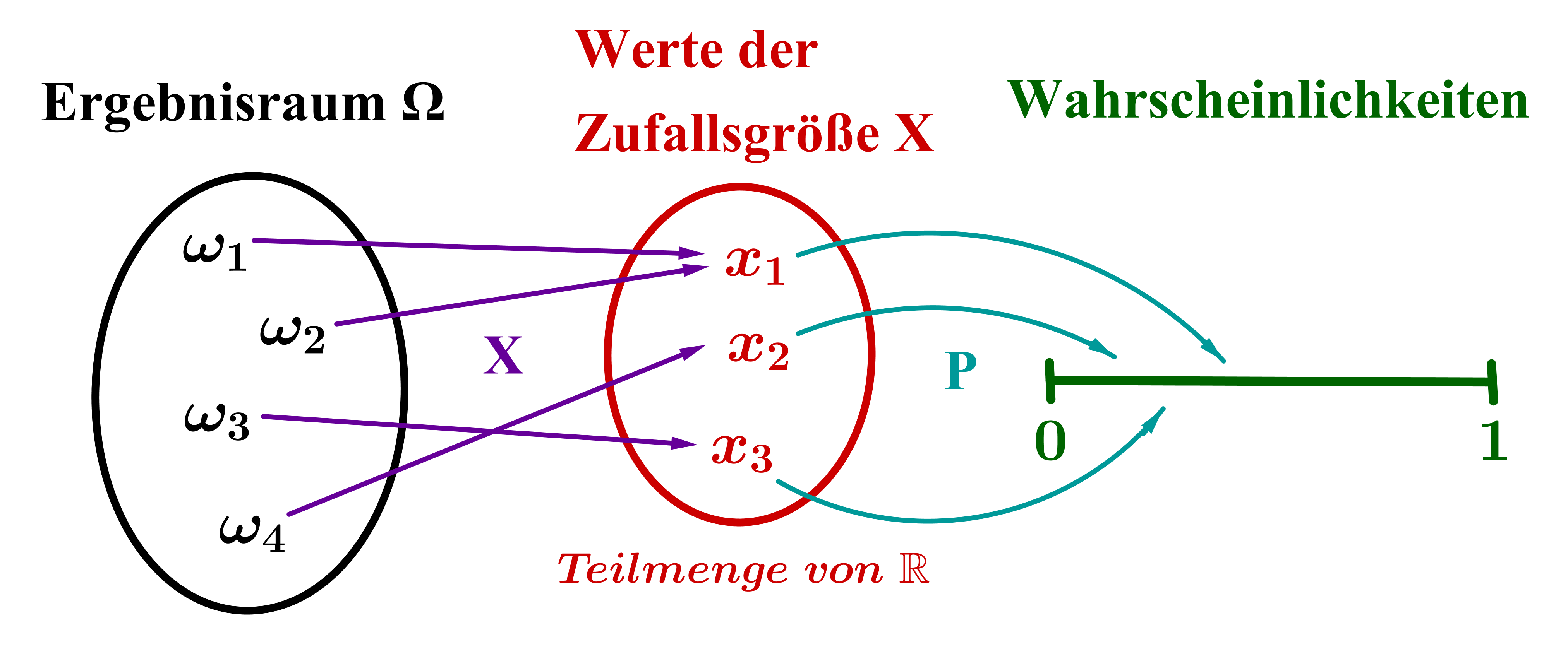
Das hat den Grund, dass wir somit bestimmte Kenngrößen ausrechnen können, die neue Informationen über das Zufallsexperiment liefern.
Erwartungswert
Der Erwartungswert einer Zufallsgröße gibt an, welcher Wert der Zufallsgröße auf lange Sicht (also bei sehr vielen Durchführungen des Zufallsexperiments) zu erwarten ist.
Er wird häufig auch mit abgekürzt und berechnet sich folgendermaßen:
Dabei sind die verschiedenen Werte, die annehmen kann.
Der Erwartungswert ist somit eine Art gewichteter Mittelwert (die Gewichtung ist deshalb wichtig, weil manche Werte der Zufallsgröße wahrscheinlicher sind als andere und deshalb stärker ins "Gewicht" fallen). Er ist im Allgemeinen kein Wert, den die Zufallsgröße annimmt.
Varianz und Standardabweichung
Die Varianz einer Zufallsgröße ist ein Maß für ihre mittlere quadratische Abweichung vom Erwartungswert (also wie stark die Werte um ihn streuen).
Sie berechnet sich folgendermaßen:
In einigen Situationen ist es allerdings günstiger, wenn die Streuung dieselbe Einheit wie die Werte der Zufallsgröße hat. Deshalb wird oft als äquivalente Kenngröße die Standardabweichung angegeben, die sich als Wurzel aus der Varianz ergibt:
10 Beispiel zu Zufallsgrößen
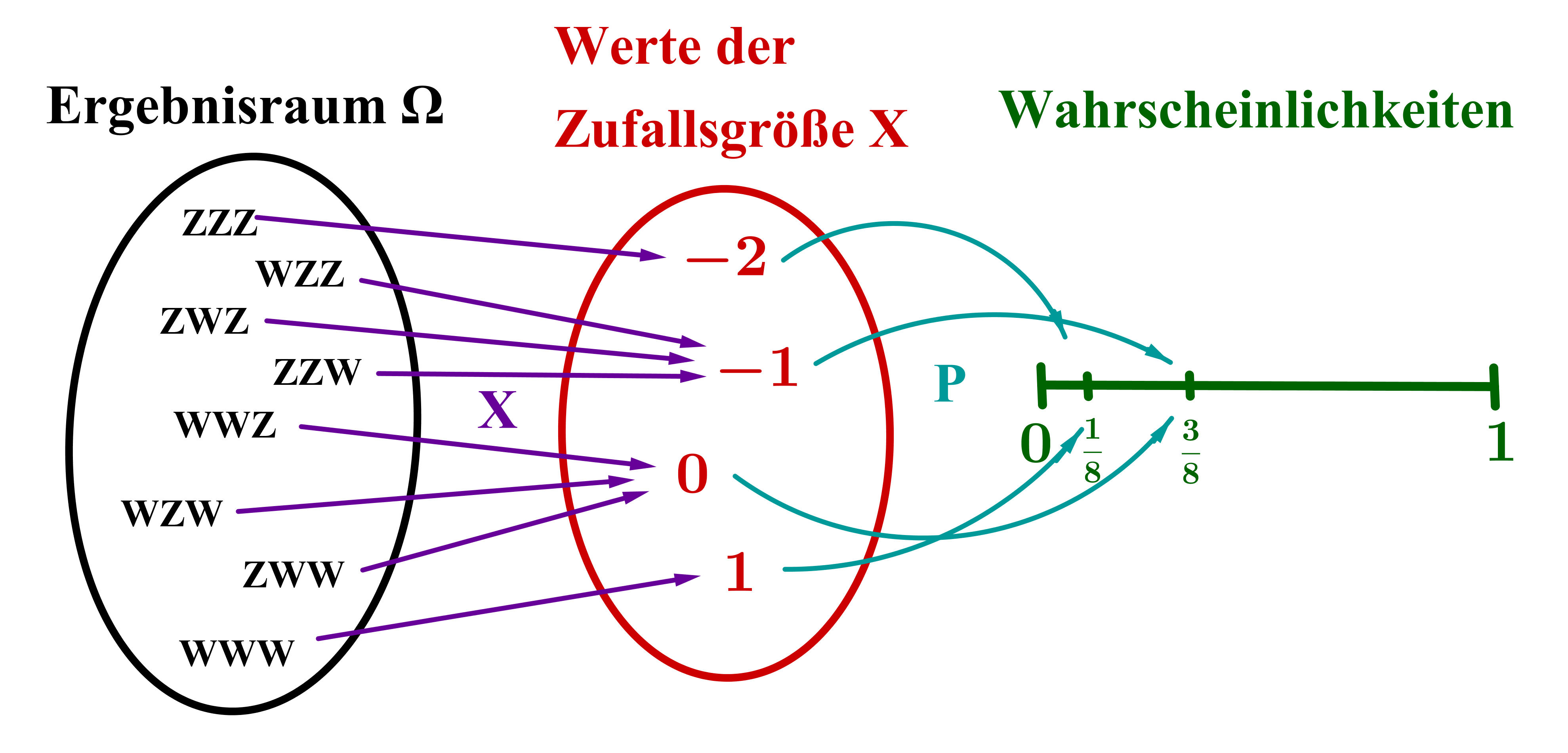
Zur Veranschaulichung betrachten wir als Beispiel folgendes einfache Glücksspiel: Nach einem Einsatz von werden drei Laplace-Münzen (also faire Münzen, bei denen Wappen und Zahl gleichberechtigt sind) geworfen. Anschließend wird die Anzahl der geworfenen Wappen in ausgezahlt.
Als Zufallsgröße wollen wir den Gewinn (also Auszahlung minus Einsatz) in betrachten.
Als mögliche Werte, die annehmen kann, ergeben sich , , und . Denn schlimmstenfalls zeigen alle drei Münzen Zahl (dann verliert man seinen Einsatz von ) und bestenfalls zeigen alle Münzen Wappen (dann erhält man als Auszahlung und somit einen Gewinn von ).
Um die zugehörige Wahrscheinlichkeitsverteilung und kumulative Verteilungsfunktion zu ermitteln, muss man sich überlegen, welche Ergebnisse zu den jeweiligen Werten von gehören. Die Resultate sind in der folgenden Tabelle zusammengefasst und in der Grafik veranschaulicht:
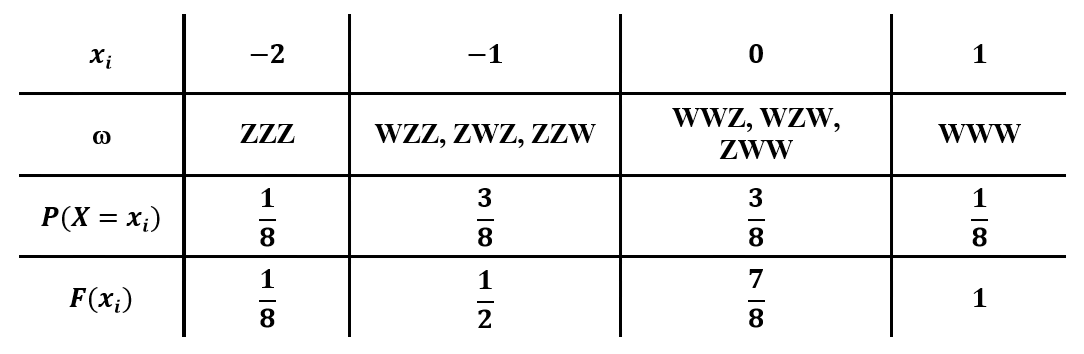
Zur Berechnung der Kenngrößen wendet man schließlich die entsprechenden Formeln an:
Erwartungswert:
Varianz:
Standardabweichung:
Bei diesem Glücksspiel ist somit auf lange Sicht ein mittlerer Gewinn von zu erwarten, wobei der tatsächliche Gewinn durchschnittlich um streut.
11 Urnenmodelle (1/2)
Vor allem in komplexeren Situationen bildet die Kombinatorik, also die Kunst des geschickten Zählens, die Grundlage für die Berechnung von Wahrscheinlichkeiten.
Dabei sind in vielen Fällen sog. Urnenmodelle hilfreich, die alle nach demselben Prinzip aufgebaut sind:
Man hat eine Urne mit unterscheidbaren Kugeln gegeben (z. B. unterschiedliche Farbe, Beschriftung, …).
Man sucht die Anzahl der Möglichkeiten, die es gibt, wenn man Kugeln nacheinander zufällig aus der Urne zieht (mit ).
Arten des Ziehens
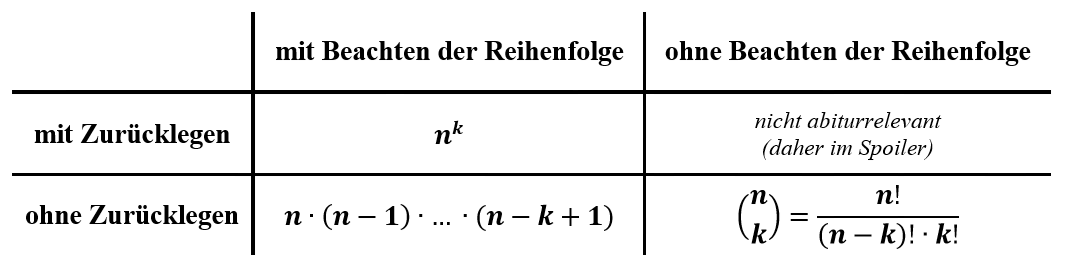
Grundsätzlich lassen sich dabei folgende Arten des Ziehens unterscheiden (im Innern der Tabelle steht jeweils die Anzahl der Möglichkeiten, die es bei dieser Ziehungsart gibt):
12 Urnenmodelle (2/2)
Ausgehend von diesen kombinatorischen Überlegungen lassen sich Wahrscheinlichkeiten in vielen Fällen recht einfach bestimmen.
Eine wichtige Anwendung ist dabei das Ziehen mit einem Griff:
Aus einer Urne mit insgesamt Kugeln, von denen rot sind, zieht man mit einem Griff Kugeln. Als Zufallsgröße interessiert man sich für die Anzahl der gezogenen roten Kugeln.
Das Ziehen mit einem Griff ist äquivalent zu der Situation, bei der man die Kugeln nacheinander ohne Zurücklegen und ohne Beachten der Reihenfolge zieht.
Daher ist die Wahrscheinlichkeit, dass von den gezogenen Kugeln genau rot sind, gegeben durch:
Beispiel
Als Beispiel betrachten wir das Glücksspiel Lotto "6 aus 49" und berechnen die Wahrscheinlichkeit für "4 Richtige".
Die Situation lässt sich mit einer Urne modellieren, in der sich insgesamt Kugeln befinden, von denen rot sind (das sind die "Richtigen"). Beim Ziehen von Kugeln soll die Zufallsgröße : "Anzahl der gezogenen roten Kugeln" den Wert annehmen.
Die Wahrscheinlichkeit für "4 Richtige" beträgt damit:
13 Aufgaben zu Urnenmodellen
Laden
Laden
14 Binomialverteilung (1/2)
Auch das Ziehen mit Zurücklegen bildet für zahlreiche Situationen eine gute Modellierungsgrundlage.
Bernoulli-Experiment
Die Basis stellt dabei das Bernoulli-Experiment dar, bei dem es sich um ein Zufallsexperiment mit nur zwei möglichen Ergebnissen handelt.
Üblicherweise werden die Ergebnisse mit Treffer bzw. Niete und die zugehörigen Wahrscheinlichkeiten mit bzw. bezeichnet.
Bernoulli-Kette
Als Erweiterung spricht man bei unabhängigen Durchführungen desselben Bernoulli-Experiments von einer Bernoulli-Kette.
Dabei wird die Länge und der Parameter der Bernoulli-Kette genannt.
Formel von Bernoulli
Mithilfe der Überlegungen zu den Urnenmodellen lässt sich die Wahrscheinlichkeit, bei einer Bernoulli-Kette mit Länge und Parameter genau Treffer zu erzielen, allgemein angeben:
Dabei ist : "Anzahl der Treffer" und .
Diese Beziehung heißt auch Formel von Bernoulli.
15 Binomialverteilung (2/2)
Die Wahrscheinlichkeitsverteilung, die zur betrachteten Zufallsgröße : "Anzahl der Treffer" bei einer Bernoulli-Kette gehört, nennt man auch Binomialverteilung.
Allgemein heißt eine Zufallsgröße binomialverteilt nach oder , wenn gilt:
kann die Werte annehmen.
mit
Dabei sind folgende Schreibweisen gebräuchlich:
(Wahrscheinlichkeitsverteilung)
(kumulative Verteilungsfunktion)
Kenngrößen der Binomialverteilung
Berechnet man für den Fall einer Binomialverteilung die Kenngrößen Erwartungswert, Varianz und Standardabweichung jeweils nach der allgemeinen Formel, so ergibt sich:
16 Beispiel zu Binomialverteilung
Als Beispiel soll im Folgenden das Drehen des nebenstehenden Glücksrads betrachtet werden. Dabei steht der rote Sektor für "Treffer" und die übrigen vier weißen Sektoren jeweils für "Niete". (Die fünf Sektoren können als gleich groß angenommen werden.)
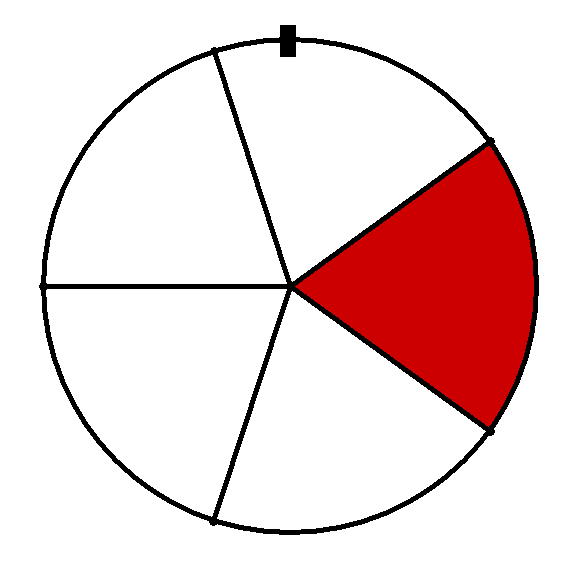
Dreht man das Glücksrad nur ein Mal, so handelt es sich dabei um ein Bernoulli-Experiment mit einer Trefferwahrscheinlichkeit .
Dreht man das Glücksrad zehn Mal hintereinander (wobei die einzelnen Drehungen als unabhängig voneinander angenommen werden), so handelt es sich dabei um eine Bernoulli-Kette der Länge mit Parameter .
Betrachtet man als Zufallsgröße : "Anzahl der Treffer bei 10 Drehungen des Glücksrads", so ist binomialverteilt nach .
Mit der Formel von Bernoulli kann somit bespielsweise die Wahrscheinlichkeit, bei 10 Drehungen 3 Treffer zu erhalten, berechnet werden:
Auf dieselbe Weise kann auch die Wahrscheinlichkeit, bei 10 Drehungen höchstens 4 Treffer zu erhalten, berechnet werden (bequemer geht es allerdings unter Zuhilfenahme eines geeigneten Tafelwerks):
Die Berechnung der Kenngrößen liefert schließlich folgendes Ergebnis:
Erwartungswert:
Varianz:
Standardabweichung:
17 Beurteilende Statistik (1/2)
Bisher sind wir immer von der (modellhaften) Situation ausgegangen, dass wir den Inhalt der Urne kennen und auf dieser Grundlage bestimmte Wahrscheinlichkeiten (als Vorhersage für das Experiment) ausrechnen können.
In der Statistik geht man nun grundsätzlich von einer anderen Problemstellung aus: Der Inhalt der Urne (man spricht auch von Grundgesamtheit) ist unbekannt und kann nicht exakt ermittelt werden (z. B. weil er zu groß ist). Deshalb zieht man eine Stichprobe und versucht, anhand ihres Ergebnisses auf die Zusammensetzung der Grundgesamtheit rückzuschließen.
Das konkrete Vorgehen läuft dabei nach folgendem Schema ab:
Zuerst formuliert man die Vermutung, die es zu überprüfen gilt, in Form einer Nullhypothese ; häufig gibt man zusätzlich eine Gegenhypothese an.
Anschließend legt man die Testgröße sowie den Stichprobenumfang fest.
Und schließlich bestimmt man die Entscheidungsregel, indem man den kritischen Bereich (also den Ablehnungsbereich von ) festlegt.
18 Beurteilende Statistik (2/2)
Prinzipiell kann bei einem Hypothesentest die Entscheidungsregel vollkommen willkürlich gewählt werden.
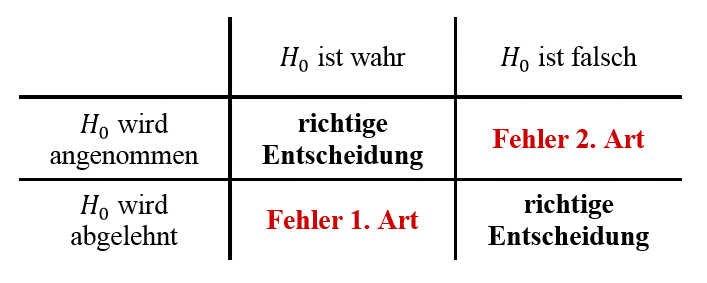
Allerdings können dabei naturgemäß zwei Arten von Fehlern unterlaufen, die man Fehler 1. Art und Fehler 2. Art nennt.
Die Tabelle rechts gibt einen Überblick über die verschiedenen Szenarien, die möglich sind.
Signifikanztest
Mithilfe der Wahrscheinlichkeitsrechnung lassen sich diese Fehler nun in gewisser Weise eingrenzen.
Bei einem Signifikanztest legt man dabei das sog. Signifikanzniveau fest; damit bezeichnet man die Obergrenze für den Fehler 1. Art (also fälschlicherweise abzulehnen).
Auf dieser Grundlage lässt sich dann ein optimaler kritischer Bereich konstruieren. Je nachdem, auf welcher Seite dieser kritische Bereich liegt, spricht man von einem rechts- bzw. linksseitigen Signifikanztest.
19 Beispiel zu Beurteilender Statistik
Als Beispiel soll die Nullhypothese, dass der Anteil defekter Bauteile in einer Produktionsserie beträgt, auf einem Signifikanzniveau von getestet werden. (Die zugehörige Gegenhypothese wäre, dass es in der Vergangenheit eine Qualitätssteigerung gegeben hat und der Anteil somit geringer ist.)
Formulieren von und
Wenn man mit den Anteil der defekten Bauteile bezeichnet, so gilt:
Festlegen von und
Als Durchführung kann man beispielsweise nacheinander 50 Bauteile der Serie zufällig ziehen und bei jedem Bauteil ermitteln, ob es defekt ist.
Als Testgröße und Stichprobenumfang ergeben sich damit:
: "Anzahl defekter Bauteile"
Konstruktion des kritischen Bereichs
Liefert die Erhebung das Ergebnis, dass nur sehr wenige Bauteile defekt sind, würde man ablehnen und stattdessen annehmen. Daher ist der kritische Bereich von der Form , wobei die Obergrenze noch zu bestimmen ist. Es handelt sich somit um einen linksseitigen Signifikanztest.
Da der Fehler 1. Art höchstens betragen darf, ist die größte ganze Zahl, für die ist.
kann als binomialverteilt nach angenommen werden, daher kann mithilfe eines geeigneten Tafelwerks ermittelt werden:
Somit ist der kritische Bereich durch gegeben.
20 Aufgabe zu Beurteilender Statistik
Laden
