Sachaufgaben mit Brüchen
Hier kannst du lernen, Brüche zum Lösen sachbezogener Probleme zu verwenden. Schaffst du sie alle?
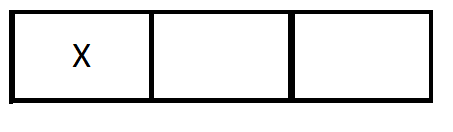
- 1
Ein Koala schläft des Tages. Wie viele Stunden schläft das Tier täglich?
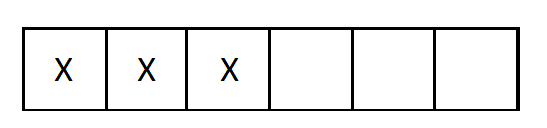
h - 2
Ein Siebenschläfer schläft des Tages. Wie viele Stunden schläft es täglich?
h - 3
Joscha ist Winzer und sein Weinfass enthält Liter Wein. Davon werden 6 Flaschen zu je 0,75 Liter und 9 Flaschen zu je 0,7 Liter abgefüllt.
Wie viel Liter hat Joscha übrig, die er selbst noch trinken kann?
- 4
Du möchtest zu deiner Geburtstagsfeier etwas ganz besonderes machen und hast dir überlegt Cocktails zu mixen. Dazu benötigst du 3 Liter Maracuja-Saft, und Johannisbeersaft. Den Maracuja-Saft gibt es allerdings nur in 0,75-Liter Flaschen und den Johannisbeersaft gibt es ausschließlich in 0,5-Liter Flaschen zu kaufen. Außerdem benötigst du zum Aufgießen noch Tonic Water, welches es in 1 Liter Flaschen zu besorgen gibt.
Wie viele Flaschen brauchst du jeweils von einer Sorte?

- 5
Karin und Uwe lesen in der Zeitung: ”Die Zuschauerzahlen für das jährlich stattfindende Open-Air-Festival in Kreischhausen schwanken in letzter Zeit stark: Während es im Jahre 2007 ein Drittel weniger Zuschauer als im Jahre 2006 gab, kamen im Jahre 2008 ein Drittel mehr Zuschauer als 2007. “Uwe meint:” Also sind es 2008 wieder genauso viele Teilnehmer wie 2006.“ Karin entgegnet: ”Das sieht zwar auf den ersten Blick so aus, aber wenn beispielsweise im Jahr 2006 . . .“
Setze den Gedanken von Karin fort. Begründe damit, dass Uwes Aussage nicht zutrifft.
- 6
Die drei Söhne des verstorbenes Piraten Käptn's erben seine 17 Golddukaten. Im Testament heißt es: ”Mein erstgeborener Sohn soll die Hälfte der Dukaten, mein zweitgeborener ein Drittel und mein jüngster ein Neuntel der Dukaten bekommen. Kein Dukate darf geteilt werden.“ Die Söhne sind ratlos. (Warum?) Sie tragen ihr Problem einem Steuermann vor, der als weiser Mann gilt. Er überlegt nicht lange und gibt ihnen den folgenden Rat: ”Ich besitze selbst eine Dukate. Davon leihe ich euch eine. Vollzieht damit die Teilung wie es das Testament verlangt. “Wie viele Dukaten bekommt jeder der Söhne? Was fällt dir auf? Hast du eine Erklärung dafür?
- 7
Bei einer Tombola wurden der Lose an Kinder und der Lose an Erwachsene verkauft. Es blieben 100 Lose übrig. Wie viele Lose wurden verkauft?
Lose - 8
Ein Elefant fraß in der ersten Woche seines Futtervorrats. In der zweiten Woche fraß er vom Rest. Danach waren noch 300 kg Futter übrig. Veranschauliche die Situation durch eine Zeichnung. Wie viel Futter war anfangs vorhanden?
kg - 9
Kristina wird 13 Jahre alt und hat zu ihrem Geburtstag 13 Freundinnen eingeladen. Zusammen mit ihrer Mutter bereitet sie das Fest vor. Zum Mittagessen soll es Würstchen mit Kartoffelsalat geben, am Nachmittag Erdbeershakes. Den Kartoffelsalat bereiten Kristina und ihre Mutter nach folgendem Rezept zu:

Berechne die Zutaten, die für 14 Personen erforderlich sind
Zum Schälen der Kartoffeln brauchen Kristina und ihre Mutter zusammen 18 Minuten. Am Abend sagt Kristina zu ihrem Bruder: „Man kann sich ausrechnen, dass wir nur 12 Minuten gebraucht hätten, wenn du uns geholfen hättest.“ Wie hat Kristina wohl gerechnet? Was meinst du dazu?
Für die Erdbeershakes benötigt Kristina Milch, die sie direkt beim Bauern holt. Für Milch hat sie bisher immer bezahlt. Wie viel kosten Milch?
€
- 10
Familie Mattmüller benötigt am Tag Liter Milch.
Wie hoch ist der Jahresverbrauch?
Wie hoch sind die Jahreskosten, wenn Liter Milch kostet?
€
- 11
Das ist ein Bild der Nationalflagge von England. Diese Fahne ist aus einem Tuch gefertigt worden, das lang und breit ist.
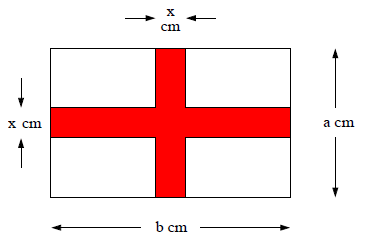
Zeichne die Figur für .
Berechne den Flächeninhalt eines der weißen Rechtecke im Inneren, wenn das Kreuz der Gesamtfläche einnimmt und die vier weißen Rechtecke kongruent sind.
m²
- 12
Eine Satire-Aufgabe:
Kanarienvogel frisst 125 Körner in Tagen. Wie viele Körner fressen 4 Kanarienvögel in 16 Tagen?
Körner
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?