Aufgaben zur Bestimmung von Stammfunktionen

Gegeben ist die Funktion $f$ mit $f(x)= 6\sqrt{x}$ .

Bestimme diejenige Stammfunktion, deren Graph durch den Punkt $(1|0)$ verläuft.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktionen bestimmen

Eine Stammfunktion $F(x)$ ist das unbestimmte Integral $\int_{ }^{ }f(x)\mathrm{d}x=F(x)$ .

Allerdings kann zu jeder Stammfunktion $F(x)$ eine beliebige Zahl $C$ addiert werden, da diese konstante Zahl beim Ableiten wegfällt. Also gilt: $\int_{ }^{ }f(x)\mathrm{d}x=F(x)+C$ mit $C \in \mathbb{R}$

Stammfunktionen von einer Potenzfunktion der Form $f(x)=k \cdot x^n$ sind für $n\neq-1$ gegeben durch:

$F(x)=\dfrac{k}{n+1}\cdot x^{n+1} + C$

Die gegebene Funktion $f(x)=6\cdot\sqrt{x}$ ist eine Potenzfunktion.

Die $\sqrt{x}$ kann als Potenz geschrieben werden: $\;\sqrt{x}=x^{\frac{1}{2}}$

Also ist $f(x)=6\cdot\sqrt{x}=6\cdot x^{\frac{1}{2}}$

Integriere mit Hilfe der Schreibweise als Potenz.

$\displaystyle \int_{ }^{ }f(x)\mathrm{d}x$	$=$	$\displaystyle \int_{ }^{ }6\cdot\sqrt{x}\mathrm{d}x$
	↓	Setze $\sqrt{x}=x^{\frac{1}{2}}$ ein.
	$=$	$\displaystyle \int_{ }^{ }6\cdot x^{\frac{1}{2}}\mathrm{d}x$
	↓	Beachte die Potenzregel. Addiere in Exponenten eine $1$ und teile durch den neuen Exponenten.
	$=$	$\displaystyle \dfrac{6}{\frac{1}{2}+1}\cdot x^{\frac{1}{2}+1}$
	↓	Vereinfache.
	$=$	$\displaystyle \dfrac{6}{\frac{3}{2}}\cdot x^{\frac{3}{2}}$
	↓	Multipliziere $6$ mit dem Kehrwert von $\frac{3}{2}$ .
	$=$	$\displaystyle 6\cdot \frac{2}{3}\cdot x^{\frac{3}{2}}$
	↓	Vereinfache.
	$=$	$\displaystyle \frac{12}{3}\cdot x^{\frac{3}{2}}$
	↓	Kürze den Bruch.
	$=$	$\displaystyle 4\cdot x^{\frac{3}{2}}$

Du hast die Stammfunktion $F(x)=4\cdot x^{\frac{3}{2}}$ erhalten. Addiere noch die Konstante $C$ .

$F(x)=4\cdot x^{\frac{3}{2}}+C$

Setze nun den Punkt $(1|0)$ in $F(x)$ ein, um die Konstante $C$ zu bestimmen.

$\displaystyle F(x)$	$=$	$\displaystyle 4\cdot x^{\frac{3}{2}}+C$
	↓	Setze den Punkt $(\textcolor{ff6600}{1}\|\textcolor{660099}{0})$ in $F(x)$ ein.
$\displaystyle \textcolor{660099}{0}$	$=$	$\displaystyle 4\cdot \textcolor{ff6600}{1}^{\frac{3}{2}}+C$
	↓	Vereinfache $1^{\frac{3}{2}}=1$ und $4\cdot1=4$ .
$\displaystyle 0$	$=$	$\displaystyle 4+C$	$\displaystyle -4$
	↓	Löse nach $C$ auf.
$\displaystyle -4$	$=$	$\displaystyle C$

Mit $C=-4$ lautet die gesuchte Stammfunktion $F(x)=4x^{\frac{3}{2}}-4$ .

Antwort: Der Graph der Funktion $F(x)=4x^{\frac{3}{2}}-4$ verläuft durch den Punkt $(1|0)$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

2

Gegeben ist die Funktion $f(x)=x+1$ .

$F(x)$ sei eine Stammfunktion von $f(x)$ und $G_F$ der Graph von $F(x)$ .

Bestimme diejenige Stammfunktion, für die gilt

$\left(\left.0\right|0\right)\ \in G_F$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Integration
$f\left(x\right)=x+1$
Integriere nun die Funktion.
$F\left(x\right)=\frac12x^2+x+c$
$c$ bestimmen
$F\left(x\right)=\frac12x^2+x+c$
Setze den gegeben Punkt $\left(\left.0\right|0\right)$ in $F\left(x\right)$ ein.
$0=\frac120^2+0+c$
$0=c$
Stammfunktion aufstellen
$F\left(x\right)=\frac12x^2+x+c$
Setze das gefundene $c$ ein.
$F\left(x\right)=\frac12x^2+x+0$
$F\left(x\right)=\frac12x^2+x$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\left(\left.0\right|1\right)\in G_F$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Integration
$f\left(x\right)=x+1$
Integriere die Funktion.
$F\left(x\right)=\frac12x^2+x+c$
c bestimmen
$F\left(x\right)=\frac12x^2+x+c$
Setze den gegeben Punkt $\left(0\vert1\right)$ in $F\left(x\right)$ ein.
$1=\frac120^2+0+c$
$1=c$
Stammfunktion aufstellen
$F\left(x\right)=\frac12x^2+x+c$
Setze das gefundene $c=1$ ein.
$F\left(x\right)=\frac12x^2+x+1$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\left(\left.1\right|0\right)\in G_F$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Integration
$f\left(x\right)=x+1$
Integriere die Funktion.
$F\left(x\right)=\frac12x^2+x+c$
$c$ bestimmen
$F\left(x\right)=\frac12x^2+x+c$
Setze den gegeben Punkt $\left(1\vert0\right)$ in $F\left(x\right)$ ein.
$0=\frac121^2+1+c$
$0=\frac32+c$
$c=-\frac32$
Stammfunktion aufstellen
$F\left(x\right)=\frac12x^2+x+c$
Setze das gefundene $c=-\frac{3}{2}$ ein.
$F\left(x\right)=\frac12x^2+x-\frac32$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

3

Notiere die Menge aller Stammfunktionen zur gegebenen Funktion.

$f\left(x\right)=x^2$

$f\left(x\right)=2x^2$

$f\left(x\right)=x$

$f\left(x\right)=-2x$

$f\left(x\right)=\frac12x^2$

$f\left(x\right)=-\frac14x$

$f\left(x\right)=x^3$

$f\left(x\right)=4x^3$

$f\left(x\right)=2$

$f\left(x\right)=x+1$

$f\left(x\right)=x^2+x-3$

$f\left(x\right)=x^n;\;n\in ℕ$

4

Bestimme für die folgende verkettete Funktion eine Stammfunktion.

$f\left(x\right)=\sin\left(12x-3\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$\int\sin\left(12x-3\right)\;\mathrm{d}x$
Integriere zunächst die äußere Funktion $\sin\left(x\right)$ .
$\int\sin\left(x\right)\;\mathrm{d}x=-\cos\left( x\right)+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss (Kettenregel).
In diesem Fall ist die innere Funktion $g\left( x\right)=\left(12 x-3\right)$ . Beim Ableiten der Funktion $g$ würde sich der Faktor $12$ beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $\sin\left(12 x-3\right)$ noch mit $\frac1{12}$ multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor 12 auszugleichen.
$\int\sin\left(12x-3\right)\;\mathrm{d}x=$
$=-\cos\left(12x-3\right)\cdot \frac1{12}+C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left(x\right)=\left(2x-3\right)^8$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left(x\right)=\left(2x-3\right)^8$
Integriere zuerst $x^8$
$\int_{ }^{ }x^8\ \mathrm{d}x=\frac{1}{9}x^9+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=\left(2x-3\right)$ ; beim Ableiten dieser Funktion würde sich der Faktor 2 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $(2x-3)^8$ noch mit $\frac1{2}$ multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor 2 auszugleichen.
$\int\left(2x-3\right)^8\;\mathrm{d}x=$
$=\frac19\left(2x-3\right)^9\;\cdot\frac12+C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left(x\right)=\sin\left(3 x\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left(x\right)=\sin\left(3 x\right)$
Integriere zunächst $\sin(x)$ .
$\int_{ }^{ }\sin(x)\ \mathrm{d}x\ =\ -\cos\left(x\right)+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=\left(3x\right)$ ; beim Ableiten dieser Funktion würde sich der Faktor 3 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $\sin\left(3x\right)$ noch mit $\frac1{3}$ multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor 3 auszugleichen.
$\int\sin\left(3x\right)\;\mathrm{d}x$
$=-\cos\left(3x\right)\cdot\frac13+ C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left( x\right)=\sin\left( x-3\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f(x) = \sin (x-3)$
Integriere zunächst $\sin(x)$ .
$\int _{ }^{ }\sin (x)\ \mathrm{d}x\ =\ -\cos \left(x\right)+C$
Da hier die Ableitung der inneren Funktion $g(x)=x-3$ , gleich 1 ist, musst du, um die Stammfunktion zu erhalten, nicht mehr nachbessern.
$\int\sin\left(x-3\right)\;\mathrm{d}x=$
$=-\cos\left(x-3\right)\cdot1+C$
$=-\cos\left(x-3\right)+ C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left( x\right)=\cos\left(- x-13\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left(x\right)=\cos \left(-x-13\right)$
Integriere zuerst die äußere Funktion $\cos(x)$ .
$\int_{ }^{ }\cos(x)\ \mathrm{d}x=\sin(x)+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=\left(-x-13\right)$ ; beim Ableiten dieser Funktion würde sich der Faktor -1 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $\cos(-x-13)$ noch mit -1 multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor -1 auszugleichen.
$\int\cos\left(-x-13\right)\;\mathrm dx$
$=\sin\left(-x-13\right)\cdot\left(-1\right)+ C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left( x\right)=-5\sin\left(3 x-2\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left(x\right)=-5\sin \left(3x-2\right)$
Integriere zunächst $\sin(x)$ .
$\int_{ }^{ }\sin(x)\ \mathrm{d}x=-\cos(x)+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=\left(3x-2\right)$ ; beim Ableiten dieser Funktion würde sich der Faktor 3 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $\sin\left(3x-2\right)$ noch mit $\frac1{3}$ multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor 3 auszugleichen.
$\int-5\cdot\sin\left(3x-2\right)\;\mathrm dx=$
$=5\cos\left(3x-2\right)\cdot\frac{1}{3}+ C$
$=\frac{5}{3}\cdot\cos\left(3x-2\right)+ C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left( x\right)=\frac1{16}\;\left(40 x-3{,}5\right)^3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left( x\right)=\frac1{16}\;\left(40 x-3{,}5\right)^3$
Berechne zuerst das Integral der äußeren Funktion $\frac{1}{16}x^3$ .
$\int_{ }^{ }\frac{1}{16}x^3\ \mathrm{d}x=\frac{1}{64}x^4+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=\left(40 x-3{,}5\right)$ ; beim Ableiten dieser Funktion würde sich der Faktor 40 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $\frac{1}{16}(40x-3{,}5)^3$ noch mit $\frac1{40}$ multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor 40 auszugleichen.
$\int\frac1{16}\;\left(40 x-3{,}5\right)^3\ \mathrm{d}x=$
$=\frac1{64}(40x-3{,}5)^4\cdot\frac1{40}+C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left( x\right)=\frac{\sin\;\left(2 x\right)}3$
Berechne zunächst die Ableitung der äußeren Funktion $\frac{\sin(x)}{3}$
$\int \frac{\sin(x)}{3}\mathrm{d}x=-\frac{1}{3}\cos(x)+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=\left(2x\right)$ ; beim Ableiten dieser Funktion würde sich der Faktor 2 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $\frac{\sin\left(2 x\right)}{3}$ noch mit $\frac1{2}$ multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor 2 auszugleichen.
$\int \frac{\sin\left(2 x\right)}{3}$
$=-\frac{\cos(2x)}{3}\cdot\frac{1}{2}+C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left( x\right)= e^{3 x+7}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left( x\right)= e^{3 x+7}$
Berechne zunächst das Integral der äußeren Funktion $e^x$
$\int e^x\ \mathrm{d}x=e^x+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=\left(3x+7\right)$ ; beim Ableiten dieser Funktion würde sich der Faktor 3 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $e^{3x+7}$ noch mit $\frac1{3}$ multipliziert werden, um den beim Nachdifferenzieren entstehenden Faktor 3 auszugleichen.
$\int e^{3 x+7}\ \mathrm{d}x =$
$=e^{3x+7}\cdot\frac{1}{3}+C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f\left( x\right)=\frac{\pi}2 e^{7 x}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
$f\left( x\right)=\frac{\pi}2 e^{7 x}$
Berechne zunächst die Stammfunktion der äußeren Funktion $\frac{\pi}{2}e^x$
$\int \frac{\pi}{2}e^x\mathrm{d}x=\frac{\pi}{2}e^x+C$
Beim Integrieren darfst du jedoch nicht außer Acht lassen, dass man beim Ableiten einer verketteten Funktion nachdifferenzieren muss. In diesem Fall ist die innere Funktion $g\left( x\right)=7x$ ; beim Ableiten dieser Funktion würde sich der Faktor 7 beim Nachdifferenzieren ergeben.
Deshalb muss die Stammfunktion zu $\frac{\pi}2 e^{7 x}$ noch mit $\frac1{7}$ multipliziert werden.
$\int \frac{\pi}2 e^{7 x}dx=$
$=\frac{\pi}2 e^{7 x}\cdot\frac{1}{7}+C$
Ergebnis: Die Stammfunktion ist:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

5

Bestimme alle Stammfunktionen für folgende komplizierteren Funktionen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktionen finden
$\int_{ }^{ }f\left(x\right)\mathrm{d}x=\int_{ }^{ }\frac{1}{x\cdot\ln x}\mathrm{d}x$
Du kannst den Bruchterm in zwei Bruchterme aufspalten, da es sich um ein Produkt von Brüchen handelt.
$\int_{ }^{ }\frac{1}{x\cdot\ln x}\mathrm{d}x=\int _{ }^{ }\frac{1\cdot 1}{x\cdot \ln x}\mathrm{d}x=\int _{ }^{ }\frac{1}{x}\cdot \frac{1}{\ln x}$
Ziehe $\frac 1 x$ in den Zähler, damit ein Bruch der Form $\frac{f'(x)}{f(x)}$ entsteht.
$\int _{ }^{ }\frac{1}{x}\cdot \frac{1}{\ln x}=\int_{}\frac{\frac1x}{\ln x}\mathrm dx$
Da $(\ln x)'= \frac 1 x$ hilft dir die Regel $\int\frac{f'(x)}{f(x)}dx = \ln |f(x)| +c$
$\int_{}\frac{\frac1x}{\ln x}\mathrm dx=\ln\left|\ln x\right|+C$
Deswegen ist
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktionen finden
$\int f\left( x\right)\mathrm{d}x=\int e^{ x- e^x}\mathrm{d}x$
Die normalen Regeln zur Integration helfen dir hier nicht weiter. Teile den Term erstmal mithilfe der Potenzgesetze auf.
$\int e^{ x- e^x}\mathrm{d}x=\int e^x\cdot e^{-e^x}\mathrm{d}x$
Überlege dir, was passiert, wenn du nur den hinteren Faktor hast und diesen ableitest: $(e^{-e^x})'= -e^x\cdot e^{-e^x}$
Die zu integrierende Funktion unterscheidet sich nur durch ein Minus! Da du in deinem Integral nicht einfach ein Minus hinzufügen kannst, setze insgesamt zwei ein, denn gemeinsam ergeben sie wieder Plus!
$\int e^x\cdot e^{-e^x}\mathrm{d}x=\int -(-e^x\cdot e^{-e^x}) dx$
Ziehe eines der beiden vor das Integral.
$\int -(-e^x\cdot e^{-e^x}) dx=-\int- e^x\cdot e^{- e^x}\mathrm{d}x$
Nun hast du innerhalb des Integrals im Integranden die oben ermittelte Ableitung von $e^{-e^x}$ . Also ist das die gesuchte Stammfunktion! Vergiss das Minus vor dem Integral nicht ;)
$-\int- e^x\cdot e^{- e^x}\mathrm{d}x=- e^{- e^x}+ C$
Deswegen ist
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

6

Vereinfache die folgenden Funktionen so weit wie möglich und bilde eine Stammfunktion.

$\displaystyle f(x)=\frac{7}{x^{-2}}$

$g(x)=\dfrac{6}{x^{-3}}+\dfrac{2}{x^{-1}}$

$h(x)=\dfrac{4}{x^{-2}} \cdot \dfrac{3}{x^2}$

$\displaystyle k(x)= \frac{3}{x^4} \cdot \frac{2}{x^{-2}}$

7

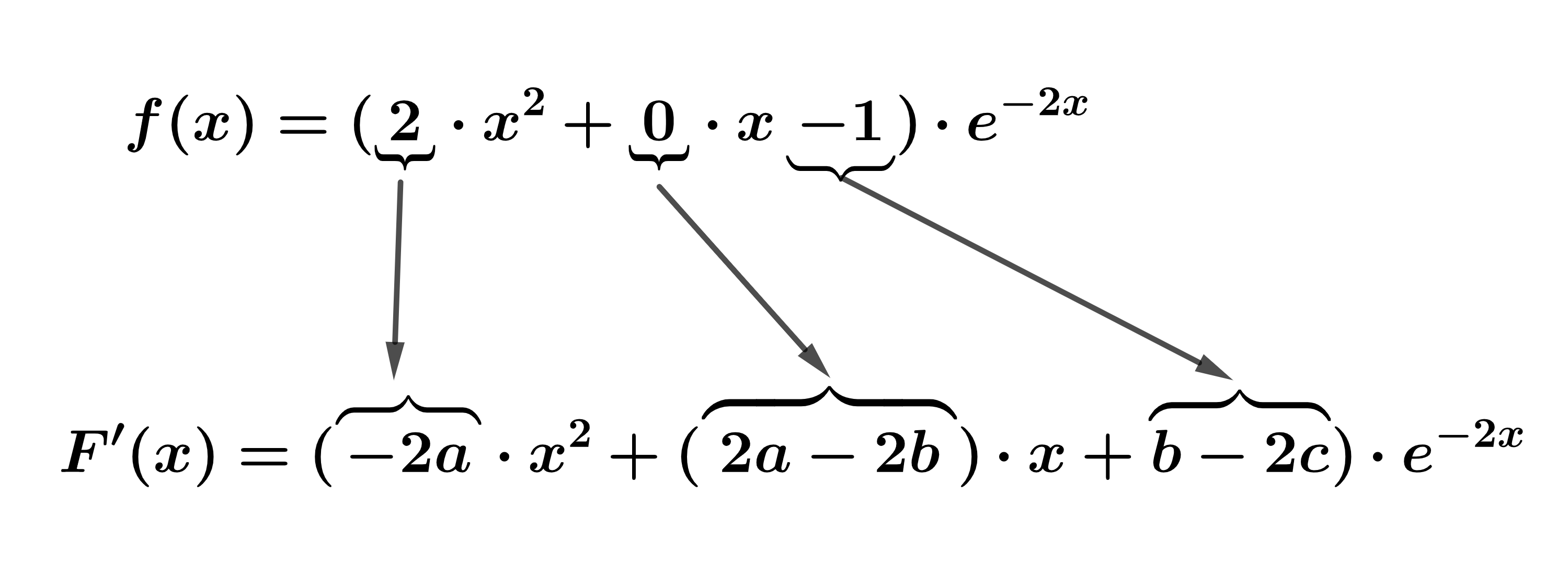
Finde eine Stammfunktion für die $e$ -Funktion mithilfe des Formansatzes.

$f(x)=(4x-2)\cdot e^{2x}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Damit $F(x)$ eine Stammfunktion von $f(x)$ ist, muss gelten $F'(x) =f(x)$ .
Bilde die Ableitung von $F(x)=(ax+b)\cdot e^{2x}$ , beachte dabei die Produkt- und Kettenregel.
$F'(x)=a\cdot e^{2x}+(ax+b)\cdot e^{2x}\cdot 2=(2ax+2b+a)\cdot e^{2x}$
Der Koeffizientenvergleich von $f(x)$ und $F'(x)$ liefert folgendes Gleichungssystem:
$\mathrm{I}\;\;\;\;\;4=2a\;\Rightarrow\;a=2$
$\mathrm{II}-2=2b+a$
Setze $a=2$ in Gleichung $\mathrm{II}$ ein $\;\Rightarrow\;-2=2b+2\;\Rightarrow\;b=-2$
Mit $a=2$ und $b=-2$ ergibt sich die allgemeine Stammfunktion zu:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Term vor der $e$ -Funktion ist linear. Verwende deshalb einen Ansatz mit einer allgemeinen linearen Funktion $ax+b$ . Der Formansatz für die Stammfunktion lautet dann $F(x)=(ax+b)\cdot e^{2x}$ . Bilde die Ableitung von $F(x)$ und führe einen Koeffizientenvergleich mit $f(x)$ durch.
$f(x)=(2x^2-1)\cdot e^{-2x}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Damit $F(x)$ eine Stammfunktion von $f(x)$ ist, muss gelten $F'(x) =f(x)$ .
Bilde die Ableitung von $F(x)=(ax^2+bx+c)\cdot e^{-2x}$ , beachte dabei die Produkt- und Kettenregel.
$F'(x)=(2a x+b)\cdot e^{2x}+(a x^2+bx+c)\cdot e^{-2x}\cdot(-2)$
$F'(x)=(2a x+b+(-2)\cdot(a x^2+bx+c))\cdot e^{-2x}$
$F'(x)=(-2a x^2-2bx-2c+2ax+b)\cdot e^{-2x}$
$F'(x)=(-2a x^2+(2a-2b) x+b-2c)\cdot e^{-2x}$
Beachte bei der Funktion $f(x)$ den Einschub des Terms $0\cdot x$ .
Der Koeffizientenvergleich von $f(x)$ und $F'(x)$ liefert folgendes Gleichungssystem:
$\mathrm{I}\;\;\;\;\;2=-2a\;\Rightarrow\;a=-1$
$\mathrm{II}\;\;\;\;0=2a-2b\;\Rightarrow\;a=b$
$\mathrm{III}-1=b-2c$
Setze $a=-1$ in $\mathrm{II}$ ein $\;\Rightarrow\;b=-1$
Setze $b=-1$ in $\mathrm{III}$ ein $\;\Rightarrow\;-1=-1-2c\;\Rightarrow\;c=0$
Mit $a=-1$ , $b=-1$ und $c=0$ ergibt sich die allgemeine Stammfunktion zu:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Term vor der $e$ -Funktion ist quadratisch. Verwende deshalb einen Ansatz mit einer allgemeinen quadratischen Funktion $ax^2+bx+c$ . Der Formansatz für die Stammfunktion lautet dann $F(x)=(ax^2+bx+c)\cdot e^{-2x}$ . Bilde die Ableitung von $F(x)$ und führe einen Koeffizientenvergleich mit $f(x)$ durch.

$\displaystyle f\left(x\right)$	$=$	$\displaystyle x^2$
$\displaystyle \int_{ }^{ }x^n\mathrm{d}x$	$=$	$\displaystyle \frac{1}{n+1}x^{n+1}+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{3}x^3+C$	$\displaystyle (C\inℝ)$

1. Linearitätseigenschaft
	↓
$\displaystyle \int_{ }^{ }2x^2\mathrm{d}x$	$=$	$\displaystyle 2\int_{ }^{ }x^2\mathrm{d}x$
	↓	Beachte $\int x^n\,\mathrm{d}x=\dfrac{1}{n+1}x^{n+1}+C$
	$=$	$\displaystyle \frac{2}{3}x^3+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{2}{3}x^3+C$	$\displaystyle (C\inℝ)$

$\displaystyle f\left(x\right)$	$=$	$\displaystyle x$
	↓	Integriere
$\displaystyle \int_{ }^{ }x\ \mathrm{d}x$	$=$	$\displaystyle \frac{1}{2}x^2+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{2}x^2+C$	$\displaystyle (C\in ℝ)$

$\displaystyle f\left(x\right)$	$=$	$\displaystyle -2x$
	↓	Integriere
$\displaystyle \int_{ }^{ }-2x\ \mathrm{d}x$	$=$
	↓	$1$ . Linearitätseigenschaft
	$=$	$\displaystyle -2\int_{ }^{ }x\ dx$
	↓	Beachte $\int x^n\,dx = \frac{1}{n+1}x^{n+1}+C$ mit $n=1$
	$=$	$\displaystyle -2\cdot\frac{1}{2}x^2+C$
	↓	Fasse zusammen.
$\displaystyle F\left(x\right)$	$=$	$\displaystyle -x^2+C$	$\displaystyle (C\in ℝ)$

1. Linearitätseigenschaft
	↓
$\displaystyle \int_{ }^{ }\frac{1}{2}x^2\ \mathrm{d}x$	$=$	$\displaystyle \frac{1}{2}\int_{ }^{ }x^2dx$
	↓	Beachte, dass $\int_{ }^{ }x^n\mathrm{d}x=\frac{1}{n+1}x^{n+1}+C$
	$=$	$\displaystyle \frac{1}{2\cdot3}x^3+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{6}x^3+C$	$\displaystyle (C\in ℝ)$

1.Linearitätseigenschaft
	↓
$\displaystyle \int_{ }^{ }-\frac{1}{4}x\ \mathrm{d}x$	$=$	$\displaystyle -\frac{1}{4}\cdot\int_{ }^{ }x\ \mathrm{d}x$
	↓	Beachte, dass $\int_{ }^{ }x^n\mathrm{d}x=\frac{1}{n+1}x^{n+1}+C$
	$=$	$\displaystyle -\frac{1}{4\cdot2}x^2+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle -\frac{1}{8}x^2+C$	$\displaystyle (C\in ℝ)$

Beachte, dass $\int_{ }^{ }x^n\mathrm{d}x=\frac{1}{n+1}x^{n+1}+C$
	↓
$\displaystyle \int_{ }^{ }x^3\mathrm{d}x$	$=$	$\displaystyle \frac{1}{4}x^4+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{4}x^4+C$	$\displaystyle (C\in ℝ)$

1.Linearitätseigenschaft
	↓
$\displaystyle \int_{ }^{ }4x^3\mathrm{d}x$	$=$	$\displaystyle 4\cdot\int_{ }^{ }x^3\mathrm{d}x$
	↓	Beachte, dass $\int_{ }^{ }x^n\mathrm{d}x=\frac{1}{n+1}x^{n+1}$
	$=$	$\displaystyle 4\cdot\frac{1}{4}x^4+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle x^4+C$	$\displaystyle (C\in ℝ)$

1.Linearitätseigenschaft
	↓
$\displaystyle \int_{ }^{ }2\ \mathrm{d}x$	$=$	$\displaystyle 2\cdot\int_{ }^{ }x^0\ \mathrm{d}x$
	↓	Beachte, dass $\int_{ }^{ }x^n\mathrm{d}x=\frac{1}{n+1}x^{n+1}+C$
	$=$	$\displaystyle 2x+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle 2x+C$	$\displaystyle (C\in ℝ)$

2. Linearitätseigenschaft
	↓
$\displaystyle \int_{ }^{ }x+1\ \mathrm{d}x$	$=$	$\displaystyle \int_{ }^{ }x\ \mathrm{d}x+\int_{ }^{ }1\ \mathrm{d}x$
	↓	Beachte, dass $\int_{ }^{ }x^n\mathrm{d}x=\frac{1}{n+1}x^{n+1}+C$
	$=$	$\displaystyle \frac{1}{2}x^2+x+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{2}x^2+x+C$	$\displaystyle (C\in ℝ)$

2.Linearitätseigenschaft
	↓
$\displaystyle \int_{ }^{ }x^2+x-3\ \mathrm{d}x$	$=$	$\displaystyle \int_{ }^{ }x^2\ \mathrm{d}x+\int_{ }^{ }x\ \mathrm{d}x-\int_{ }^{ }3\ \mathrm{d}x$
	↓	Beachte, dass $\int_{ }^{ }x^n\mathrm{d}x=\frac{1}{n+1}x^{n+1}+C$
	$=$	$\displaystyle \frac{1}{3}x^3+\frac{1}{2}x^2-3x+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{3}x^3+\frac{1}{2}x^2-3x+C$	$\displaystyle (C\in ℝ)$

$\displaystyle f\left(x\right)$	$=$	$\displaystyle x^n\ ;\ n\ ∈\ ℕ$
	↓	Integriere
$\displaystyle \int_{ }^{ }x^ndx$	$=$	$\displaystyle \frac{1}{n+1}x^{n+1}+C$
$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{n+1}x^{n+1}+C$	$\displaystyle (C\in ℝ)$

$\displaystyle f\left(x\right)$	$=$	$\displaystyle \frac{7}{x^{-2}}$
	↓	Wende nun das Potenzgesetz für negative Exponeneten an.
	$=$	$\displaystyle 7\cdot x^{-\left(-2\right)}$
	↓	Vereinfache den Exponenten.
	$=$	$\displaystyle 7x^2$

$\displaystyle F\left(x\right)$	$=$	$\displaystyle \frac{1}{3}\cdot7\cdot x^3+C$
	$=$	$\displaystyle \frac{7}{3}x^3+C$
	↓	mit $C\in \mathbb{R}$

$\displaystyle g\left(x\right)$	$=$	$\displaystyle \frac{6}{x^{-3}}+\frac{2}{x^{-1}}$
	↓	Wende das Potenzgesetz für negative Exponenten an.
	$=$	$\displaystyle 6\cdot x^{-\left(-3\right)}+2\cdot x^{-\left(-1\right)}$
	↓	Vereinfache die Exponenten.
	$=$	$\displaystyle 6\cdot x^3+2\cdot x^1$
	$=$	$\displaystyle 6x^3+2x$

$\displaystyle G\left(x\right)$	$=$	$\displaystyle 6\cdot\frac{1}{4}\cdot x^4+2\cdot\frac{1}{2}\cdot x^2+C$
	↓	mit $C\in \mathbb{R}$
	$=$	$\displaystyle \frac{3}{2}x^4+x^2+C$

$\displaystyle h\left(x\right)$	$=$	$\displaystyle \frac{4}{x^{-2}}\cdot\frac{3}{x^2}$
	↓	Benutze das Potenzgesetz zu negativen Exponenten um $\dfrac{4}{x^{-2}}$ umzuformen.
	$=$	$\displaystyle 4x^{-\left(-2\right)}\cdot\frac{3}{x^2}$
	↓	Vereinfache den Exponenten.
	$=$	$\displaystyle 4x^2\cdot\frac{3}{x^2}$
	↓	Schreibe $4x^2$ in den Zähler.
	$=$	$\displaystyle \frac{4\cdot x^2\cdot3}{x^2}$
	↓	Fasse den Zähler zusammen.
	$=$	$\displaystyle \frac{12\cdot x^2}{x^2}$
	↓	Kürze den Faktor $x^2$ .
	$=$	$\displaystyle 12$

$\displaystyle h\left(x\right)$	$=$	$\displaystyle \frac{4}{x^{-2}}\cdot\frac{3}{x^2}$
	↓	Fasse die Brüche zu einem Bruch zusammen.
	$=$	$\displaystyle \frac{4\cdot3}{x^{-2}\cdot x^2}$
	↓	Vereinfache den Zähler.
	$=$	$\displaystyle \frac{12}{x^{-2}\cdot x^2}$
	↓	Berechne den Nenner mit Hilfe der Potenzgesetze.
	$=$	$\displaystyle \frac{12}{x^{-2+2}}$
	↓	Vereinfache den Exponenten im Nenner.
	$=$	$\displaystyle \frac{12}{x^0}$
	↓	Beachte: $x^0=1$ .
	$=$	$\displaystyle \frac{12}{1}$
	$=$	$\displaystyle 12$

$\displaystyle k\left(x\right)$	$=$	$\displaystyle \frac{3}{x^4}\cdot\frac{2}{x^{-2}}$
	↓	Wende das Potenzgesetz zu negativen Exponenten an.
	$=$	$\displaystyle \frac{3}{x^4}\cdot2x^{-\left(-2\right)}$
	↓	Vereinfache den Exponenten.
	$=$	$\displaystyle \frac{3}{x^4}\cdot2x^2$
	↓	Schreibe $\displaystyle 2x^2$ in den Zähler.
	$=$	$\displaystyle \frac{3\cdot2x^2}{x^4}$
	↓	Vereinfache den Zähler.
	$=$	$\displaystyle \frac{6x^2}{x^4}$
	↓	Kürze mit $\displaystyle x^2$ .
	$=$	$\displaystyle \frac{6}{x^2}$
	↓	Wende wieder das Potenzgesetz zu negativen Exponenten an.
	$=$	$\displaystyle 6x^{-2}$

Aufgaben zur Bestimmung von Stammfunktionen

Integration

ccc bestimmen

Stammfunktion aufstellen

Hast du eine Frage oder Feedback?

Integration

c bestimmen

Stammfunktion aufstellen

Hast du eine Frage oder Feedback?

Integration

ccc bestimmen

Stammfunktion aufstellen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösungsvariante 1

Lösungsvariante 2

Bilden der Stammfunktion

Hast du eine Frage oder Feedback?

Lösungsvariante 1:

Lösungsvariante 2:

Bilden der Stammfunktion

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$c$ bestimmen

$c$ bestimmen