Aufgaben zur Polynomdivision

1

Führe die Polynomdivision durch. Faktorisiere anschließend das Polynom des Dividenden durch Bestimmung all seiner Nullstellen.

$(x^3+2x^2-x-2):(x-1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision

$\def\arraystretch{1.25} \begin{array}{l}\;\;(x^3+2x^2-x-2):(x-1)=x^2+3x+2\\\underline{-(x^3-1x^2)\;\;\;\;}\\\;\;\;\;\;\;\;\;3x^2-x\\\;\;\;\;\;\underline{-(3x^2-3x)\;\;\;\;}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2x-2\\\;\;\;\;\;\;\;\;\;\;\;\underline{-(2x-2)}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$

$\;\;\Rightarrow\;\;$ Neue Funktion : $f\left(x\right)=x^2+3x+2$

Verbleibende Nullstellen berechnen

$\displaystyle f\left(x\right)$	$=$	$\displaystyle x^2+3x+2$
	↓	Gleich $0$ setzen.
$\displaystyle 0$	$=$	$\displaystyle x^2+3x+2$
	↓	Mitternachtsformel anwenden.
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{-3\pm\sqrt{3^2-4\cdot1\cdot2}}{2\cdot1}$
	↓	Unter der Wurzel ausmultiplizieren.
	$=$	$\displaystyle \dfrac{-3\pm\sqrt{9-8}}{2}$
	↓	Wurzelziehen.
	$=$	$\displaystyle \dfrac{-3\pm1}{2}$

$x_2=\dfrac{-3+1}2=\dfrac{-2}2=-1$

$x_3=\dfrac{-3-1}2=\dfrac{-4}2=-2$

Faktorisierung

$x^3+2x^2-x-2=(x-1)(x+1)(x+2)$ ist die gesuchte Faktorisierung, hier sogar eine Linearfaktordarstellung.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$(4x^3-4x):(x+1)$

$(\frac23x^3+2x^2-\frac83):(x+2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision

$\def\arraystretch{2} \begin{array}{l}\;\;(\dfrac23x^3+2x^2-\dfrac83):(x+2)=\dfrac23x^2+\dfrac23x-\dfrac43\\\underline{-(\dfrac23x^3+\dfrac43x^2)\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\dfrac23x^2-\dfrac83\\\;\;\;\;\;\;\;\;\;\underline{-(\dfrac23x^2+\dfrac43x)\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-\dfrac43x-\dfrac83\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(-\dfrac43x-\dfrac83)\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$

Nullstellenberechnung

$\displaystyle \dfrac{2}{3}x^2+\dfrac{2}{3}x-\dfrac{4}{3}$	$=$	$\displaystyle 0$
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{-\dfrac{2}{3}\pm\sqrt{\left(\dfrac{2}{3}\right)^2-4\cdot\left(\dfrac{2}{3}\right)\cdot\left(-\dfrac{4}{3}\right)}}{\dfrac{4}{3}}$
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{-\dfrac{2}{3}\pm\sqrt{\dfrac{36}{9}}}{\dfrac{4}{3}}$
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{-\dfrac{2}{3}\pm\dfrac{6}{3}}{\dfrac{4}{3}}$

$x_2=1$

$x_3=-2$

$\dfrac23x^3+2x^2-\dfrac83=\dfrac23(x+2)^2(x-1)$ ist die Faktorisierung, hier sogar eine Linearfaktorzerlegung des Terms. Dieser hat für $x=-2$ eine doppelte Nullstelle.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$(x^4-8x^2-9):(x-3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
$\def\arraystretch{1.25} \begin{array}{l}\;\;\;(x^4-8x^2-9):(x-3)=x^3+3x^2+x+3\\\underline{-(x^4-3x^3)}\\\;\;\;\;\;\;\;\;3x^3-8x^2\\\;\;\;\;\;\;\underline{-(3x^3-9x^2)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x^2-9\\\;\;\;\;\;\;\;\;\;\;\;\underline{-(x^2-3x)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;3x-9\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(3x-9)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$
$\Rightarrow$ Neue Funktion: $f\left(x\right)=x^3+3x^2+x+3$
Als ganzzahlige Nullstellen des Terms $x^3+3x^2+x+3$ kommen nur die Teiler des konstanten Gliedes $3$ in Frage.
Also die vier Zahlen: $\pm1,\pm3$ .
Einsetzen ergibt $f(-3)=-28+27-3+3=0$ . Daneben erhält man: $f(\pm1) \neq0$ und $f(+3) \neq0$ .
$x=-3$ ist also die einzige ganzzahlige Nullstelle.
Somit muss die Polynomdivision $f(x):(x+3)$ aufgehen.
$\def\arraystretch{1.25} \begin{array}{l}\;\;(x^3+3x^2+x+3):(x+3)=x^2+1\\\underline{-(x^3+3x^2)\;\;\;\;\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;x+3\\\;\;\;\;\;\;\;\;\;\underline{-(x+3)\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$
$\Rightarrow$ Neue Funktion: $f\left(x\right)=x^2+1$
Verbleibende Nullstellen berechnen
$\displaystyle x^2+1$ $=$ $\displaystyle 0$ $\displaystyle -1$
$\displaystyle x^2$ $=$ $\displaystyle -1$
$\Rightarrow$ keine weiteren Nullstellen , da nicht lösbar in $\mathbb{R}$ .
Für den ursprünglichen Funktionsterm $x^4-8x^2-9$ erhält man somit die folgende Faktorisierung mit zwei Linearfaktoren und einen quadratischen Faktor.
$x^4-8x^2-9=(x-3)(x+3)(x^2+1)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

2

Gegeben ist die Gleichung der Geraden $g:\;y=-x+3$

und die Gleichung der ganzrationalen Funktion $f:\;y=0{,}5x^3-3x^2+4{,}5x$ .

Berechne die Schnittpunkte von $G_f$ und $G_g$ .

Errate dazu eine Lösung der Schnittgleichung und berechne die weiteren Lösungen mit Hilfe der Polynomdivision.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision

Schnittpunkte berechnen

Die beiden Funktionen haben einen Schnittpunkt, wenn sie für einen gleichen x-Wert denselben y-Wert haben. Setze also die Funktionen $f$ und $g$ gleich. Die Funktionen lauten:

$\def\arraystretch{1.25} \begin{array}{rcl} &&&f(x)&=&g(x)&\\0{,}5x^3&-3x^2&+4{,}5x& &=&-x+3&|-3+x\\ 0{,}5x^3&-3x^2&+5{,}5x&-3&=&0\end{array}$

Für Polynome vom Grad 3 musst du eine Nullstelle erraten. Alle weiteren Nullstellen lassen sich dann mit einer Polynomdivision ermitteln.

Eine Nullstelle von $0{,}5x^3-3x^2+5{,}5x-3$ ist $x_1=1$ , denn

\displaystyle 0{,}5 \cdot 1^3-3 \cdot 1^2+5{,}5 \cdot 1-3 = 0{,}5 - 3 + 5{,}5 -3 =0

Um den ersten Schnittpunkt von $f$ und $g$ zu bestimmen, kannst du nun $x_1=1$ entweder in $f$ oder $g$ einsetzen.

Einsetzen in $f$ ergibt:

$f\left(1\right)=-1+3=2$

Der Schnittpunkt ist dann: $S_1=\left(1\vert2\right)$

Polynomdivision

Wende nun die Polynomdivision auf folgende Gleichung an:

$0{,}5x^3-3x^2+5{,}5x-3=0$

$\def\arraystretch{1.25} \begin{array}{l}\;\;\;(0{,}5x^3-3x^2\;+5{,}5x-3):(x-1)=0{,}5x^2-2{,}5x+3\\\underline{-(0{,}5x^3-0{,}5x^2)\;\;\;\;\;\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;-2{,}5x^2+5{,}5x\\\;\;\;\;\;\;\;\;\;\;\underline{-(-2{,}5x^2+2{,}5x\;\;)\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;3x-3\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(3x-3)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$

Verbleibende Nullstellen berechnen

Von $0{,}5x^2-2{,}5x+3$ kannst du nun noch die beiden Nullstellen bestimmen. Nutze hierfür beispielsweise die Mitternachtsformel.

$0{,}5x^2-2{,}5x+3=0$

$\def\arraystretch{1.25} \begin{array}{rcl}\Rightarrow x_{2{,}3}&=&\frac{2{,}5\pm\sqrt{(-2{,}5)^2-4\cdot0{,}5\cdot3}}{(2\cdot0{,}5)}\\&=&\frac{2{,}5\pm\sqrt{0{,}25}}1\\&=&\frac{2{,}5\pm0{,}5}1\end{array}$

$x_2=\frac{2{,}5+0{,}5}1=\frac31=3$

$x_3=\frac{2{,}5-0{,}5}1=\frac21=2$

Die Nullstellen von $0{,}5x^3-3x^2+5{,}5x-3$ sind also:

\displaystyle 0{,}5 \cdot 1^3-3 \cdot 1^2+5{,}5 \cdot 1-3 = 0{,}5 - 3 + 5{,}5 -3 =0

weitere Schnittpunkte berechnen

Den zweiten und dritten Schnittpunkt von $f$ und $g$ , kannst du nun bestimmen, indem du $x_2=3$ und $x_3=2$ in $f$ oder $g$ einsetzt.

Einsetzen in $f$ ergibt:

$f(3)=-3 +3 = 0 \Rightarrow S_2(3|0)$
$f(2)=-2+3=1 \Rightarrow S_3(2|1)$

Schnittpunkte

Die Schnittpunkte der beiden Funktionen liegen bei $S_1(1\vert2)$ , $S_2(3\vert0)$ und $S_3(2\vert1)$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

3

Vergleiche die Schritte der gewöhnlichen schriftlichen Division am Beispiel $2998:14$ mit der Polynomdivision $(2x^3+9x^2+9x+8):(x+4)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision

Zahlenangaben wie 2998 und 14 sind Schreibweisen für Zahlen im Dezimalsystem, einem sogenannten Stellenwertsystem mit der Basis 10.

$\def\arraystretch{1.25} \begin{array} {rrcl}\text{Es gilt:} &2998 &= &2\cdot10^3+9\cdot10^2+9\cdot10+8\\ \text{und} &14 &= &1\cdot10+4\end{array}$

Ersetzt man die Basis 10 durch eine Variable $x$ , so entspricht die Division der beiden natürlichen Zahlen 2998 und 14 unmittelbar einer Polynomdivision:

\displaystyle 0{,}5 \cdot 1^3-3 \cdot 1^2+5{,}5 \cdot 1-3 = 0{,}5 - 3 + 5{,}5 -3 =0

Durchführung der Zahlendivision

$\begin {array} {l}\phantom{-}2998:14 = 214 + \frac{2}{14}\\\color{red}{-}\underline{28}\\\phantom{-2}19\\\phantom{}\color{red}{-}\underline{14}\\\phantom{-28}58\\\phantom{2}\color{red}{-}\underline{56}\\\phantom{-289}2 \;\;\;\color{red}{\text{Rest}}\end{array}$

Durchführung der Polynomdivision

$\def\arraystretch{1.25} \begin{array} {l}\phantom{-} (2x^3+9x^2+9x+8):(x+4) = 2x^2 +x + 5 -\displaystyle\frac{12}{x+4}\\\;\color{red}{-}(\underline{2x^3+8x^2})\\\phantom{-2(2x^3+}\;x^2+9x\\\phantom{-2(x^3} \color{red}{-}(\underline{x^2+4x})\\\phantom{-(2x^3+9x^2+2} 5x+8\\\phantom{-(2x^3+9x^2}\; \color{red}{-}(\underline{5x+20})\\\phantom{-2x^3+9x^2+9x+8} -12 \;\;\;\;\color{red}{\text{Rest}}\end{array}$

Du hast schon früh erfahren, dass die Division zweier natürlicher Zahlen oft "nicht aufgeht". Dies bedeutet dann, dass das Ergebnis der Division ein gemischter Bruch ist.

Hier: $2998:14\;=\;214\;+\;\frac17=214\frac17$ .

Bei der Polynomdivision bedeutet das "Nichtaufgehen" der Division, dass das Ergebnis eine Summe oder Differenz aus einer ganzrationalen Funktion und einer echt gebrochenrationalen Funktion ist.

Hier: $2x^2+x+5$ und $\displaystyle-\frac{12}{x+4}$ .

Lass dich nicht verwirren:

Setze in das Ergebnis der Polynomdivision $x=10$ ein, so ergibt sich natürlich auch $214\frac17$ als Zahlenergebnis.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

4

Wie sicher beherrscht du das Verfahren der Polynomdivision? Führe folgende Polynomdivisionen durch!

$(-2x^3+3x^2+2x-3):(-2x+3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Benutze das Verfahren der Polynomdivision um diese Aufgabe zu lösen.
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-} (-2x^3+3x^2+2x-3):(-2x+3)=x^2-1\\\color{red}{-(}\underline{-2x^3+3x^2}\color{red}{)}\\\hphantom{(-2x}0\;\;\;+\;0 \;\; +2x-3\\\hphantom{(-2x^3+3x^2+}\,\color{red}{-(}\underline{2x-3}\color{red}{)}\\\hphantom{(-2x^3+3x^2+2x-3}0\end{array}$
Es gilt also:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(-2x^3+3x^2+2x-3):(x^2-1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Benutze das Verfahren der Polynomdivision um diese Aufgabe zu lösen.
Hinweis:
Schreibe bei einer Polynomdivision Glieder mit gleichem Exponenten möglichst immer untereinander. Das Verfahren wird dadurch übersichtlicher und du vermeidest Rechenfehler.
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-}(-2x^3+3x^2+2x-3):(x^2-1)=-2x+3\\ \color{red}{-(}\underline{-2x^3 \phantom{+3x^21} +2x}\color{red}{)}\\\hphantom{(-2x^3+3}3x^2\phantom{+2x1} -3\\\hphantom{-2x^3x^2}\color{red}{-(}\underline{3x^2\phantom{+2x1} -3}\color{red}{)}\\\hphantom{-2x^2+3x^2+2x-31}0\end{array}$
Es gilt also:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^4-x^3-21x^2+x+20):(x^2+5x+4)$

Benutze das Verfahren der Polynomdivision um diese Aufgabe zu lösen.
$\def\arraystretch{1.25} \begin{array}{l}\;\;\;(x^4-x^3-21x^2\;\;\;\;+x+20):(x^2+5x+4)=x^2-6x+5\\\underline{-(x^4+5x^3+4x^2)\;\;\;\;}\\\;\;\;\;\;\;\;\;\;-6x^3-25x^2\;\;\;+x\\\;\;\;\;\;\underline{-(-6x^3-30x^2-24x)\;\;\;\;}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;5x^2+25x+20\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(5x^2+25x+20)}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(2x^3+1-x^2+x^4):(x^4-x^2+2x^3+1)$

Achtung Falle!
Nach dem Ordnen beider Polynome stellst du fest, dass das Dividendenpolynom und das Divisorpolynom gleich sind. Der Wert der Division ist demnach $1$ . Eine Polynomdivision entfällt somit.
$(x^4+2x^3-x^2+1):(x^4+2x^3-x^2+1)=1$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(3x^2+1):(2x^3-1)$

Achtung Falle!
Das Verfahren einer Polynomdivision entfällt, wenn der Grad des Divisorpolynoms größer ist als der Grad des Dividendenpolynoms.
Der Wert des Quotienten ist der Bruchterm aus beiden Polynomen.
$(3x^2+1):(2x^3-1)=\displaystyle \frac{3x^2+1}{2x^3-1}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^5-x^4+3x-3):(x-1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Benutze das Verfahren der Polynomdivision um diese Aufgabe zu lösen.
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-} (x^5-x^4+3x-3):(x-1)=x^4+3\\\color{red}{-(}\underline{x^5-x^4}\color{red}{)}\\\hphantom{(-(x^5-}\;0\;+3x-3\\\hphantom{(-2x^3+3}\,\color{red}{-(}\underline{3x-3}\color{red}{)}\\\hphantom{(-2x^3+3x^2+2}\;\;\;0\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^3+1{,}5x^2-0{,5}):(x-0{,}5)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Benutze das Verfahren der Polynomdivision um die Aufgabe zu lösen.
$(x^3+1{,}5x^2-0{,5}):(x-0{,}5)$
Im Dividendenpolynom fehlt das Monom mit $x$ . Ergänze $0x=0$ im Dividendenpolynom, damit du das Verfahren der Polynomdivision wie gewohnt anwenden kannst.
$(x^3+1{,}5x^2+0-0{,5}):(x-0{,}5)$
Wende nun das Verfahren der Polynomdivision an.
$\def\arraystretch{1.25} \begin{array}{l}\;\;(x^3+1{,}5x^2+0-0{,}5):(x-0{,}5)=x^2+2x+1\\\underline{-(x^3-0{,}5x^2)\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2x^2+0\\\;\;\;\;\;\;\;\;\;\;\;\underline{-(2x^2-x)\;\;\;\;}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x-0{,}5\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(x-0{,}5)}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^2+1):(x-1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Benutze das Verfahren der Polynomdivision um die Aufgabe zu lösen.
$(x^2+1):(x-1)$
Im Dividendenpolynom fehlt das Monom mit $x$ . Ergänze $0x=0$ im Dividendenpolynom, damit du das Verfahren der Polynomdivision wie gewohnt anwenden kannst.
$(x^2+0+1):(x-1)$
Wende nun das Verfahren der Polynomdivision an.
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-}(x^2+0+1):(x-1)=x+1+\displaystyle\frac{2}{x-1}\\\color{red}{-(}\underline{x^2-x}\color{red}{)}\\\hphantom{(x^2+0}\space x+1\\\hphantom{(x^2+}\color{red}{-(}\underline{x-1}\color{red}{)}\\\hphantom{(x^2+1): )x}2\quad\leftarrow \text{Rest}\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(4x^5-x^4):(2x^2-x+1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Wende zum Lösen dieser Aufgabe das Verfahren der Polynomdivision an.
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-}(4x^5-\;\,x^4):(2x^2-x+1)=2x^3+0{,}5x^2-0{,}75x-0{,}625+\displaystyle \frac{0{,}125x+0{,}625}{2x^2-x+1}\\\color{red}{-(}\underline{4x^5-2x^4+\;2x^3}\color{red}{)}\\\hphantom{(4x^5-x^4}x^4-\;2x^3\\\hphantom{(4x^5-}\;\color{red}{-(}\underline{x^4-0{,}5x^3+0{,}5x^2}\color{red}{)}\\\hphantom{(4x^5--x^4}-1{,}5x^3-0{,}5x^2\\\hphantom{(4x^5-x^4}\color{red}{-(}\underline{-1{,}5x^3+0{,}75x^2-0{,}75x}\color{red}{)}\\\hphantom{(4x^5-x^4):(2x^2-}\,-1{,}25x^2+\,0{,}75x\\\hphantom{(4x^5-x^4):(2x^2}\;\color{red}{-(}\underline{-1{,}50x^2+\,0{,}625x-0{,}625}\color{red}{)}\\\hphantom{(4x^5-x^4):(2x^2-x+1):(2x^2}0{,}125x+0{,}625\quad\text{Restpolynom}\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Warum einfach, wenn's auch umständlich geht?
Das Ergebnis der nachfolgenden Division bestätigt man leicht mit dem Distributivgesetz der Division:
Kannst du den Wert des Quotienten aber auch über eine Polynomdivision berechnen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Lösen mit Polynomdivision
Um diese Aufgabe zu lösen, solltest du das Verfahren der Polynomdivision kennen.
Polynome unterscheidet man unter anderem nach ihrem Grad, dem höchsten Exponenten der vorkommenden Potenzglieder.
Eine Konstante, wie die Zahl $5$ , kann deshalb wegen $5=5\cdot x^0$ als Polynom 0. Grades betrachtet werden.
Der zu berechnende Quotient kann demnach als Polynomdivision eines Polynoms 3.Grades durch ein Polynom 0.Grades angesehen werden.
Die charakteristischen dreischrittigen Arbeitsvorgänge $\text{Division}\rightarrow\text{Multiplikation}\rightarrow\text{Subtraktion}$ ergeben sich hier wie folgt:
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{\text{1. Restpolynom}}(10x^2-5x+1):5={\color{red}2x^2}{\color{blue}-x}{\color{green}+0{,}2}\\\hphantom{\text{1. Restpolyno}}{\color{red}-}\underline{10x^2 \quad \quad\quad}\\{\color{red}\text{1. Restpolynom}}\quad \quad {\color{red}-5x+1}\\\hphantom{\text{1. Restpolynom}}\quad \quad {\color{red}+}\underline{5x \quad\; }\\\hphantom{2x+}{\color{blue}\text{2. Restpolynom}}\quad \quad\;\; {\color{blue}+1}\\\hphantom{2x+3+4+10x^2+2x+}\;\;\,\underline{{\color{red}-}\,1}\\\hphantom{2x+3+2}\color{green}{\text{3. Restpolynom}}\quad \,\color{green}{0}\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^3+3x^2-4x-12):(x-2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Benutze das Verfahren der Polynomdivision um diese Aufgabe zu lösen.
$\def\arraystretch{1.25} \begin{array}{l}\phantom{-}\ (x^3+3x^2-4x-12):(x-2)=x^2+5x+6 \\-\underline{(x^3-2x^2)}\\\phantom{-(x^3-1}5x^2-4x\\\phantom{(x^3+}-\underline{(5x^2-10x)}\\\phantom{-(x^3+3x^2-x}6x-12\\\phantom{(x3+3x^2-}-\underline{(6x-12)}\\\phantom{-(x^3+3x^2-4x-12}0\end{array}$
Es gilt also:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(-4x+5x^2-3+2x^3):(2x+1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Benutze das Verfahren der Polynomdivision um diese Aufgabe zu lösen.
Bevor du jedoch die Polynomdivision dürchführen kannst, musst du erst den Dividenden ordnen:
$(-4x+5x^2-3+2x^3)=(2x^3+5x^2-4x-3)$
Berechne nun $(2x^3+5x^2-4x-3):(2x+1)$ mit dem Verfahren der Polynomdivision:
$\def\arraystretch{1.25} \begin{array}{l}\phantom{-}(2x^3+5x^2-4x-3):(2x+1)=x^2+2x-3\\-\underline{(2x^3+x^2)}\\\phantom{-(2x^3+(}4x^2-4x\\\phantom{2x^3+}-\underline{(4x^2+ 2x)}\\\phantom{(2x^3++5x^2}-6x-3\\\phantom{2x^3+5x^2}-\underline{(-6x-3)}\\\phantom{(2x^3+5x^2-4x-3)}0\end{array}$
Es gilt also:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^4+4x^3+2x-3):(x+2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Verwende das Verfahren der Polynomdivision um die Aufgabe zu lösen.
Im Dividenden fehlt das Monom mit $x^2$ . Ergänze deshalb $0 \cdot x^2=0$ im Dividenden:
$(x^4+4x^3+2x-3)=(x^4+4x^3+0+2x-3)$
Benutze nun das Verfahren der Polynomdivision:
$\def\arraystretch{2} \begin{array}{l}\phantom{-}(x^4+4x^3+0+2x-3):(x+2)=x^3+2x^2-4x+10+\left(\dfrac {-23}{x+2}\right)\\-\underline{(x^4+2x^3)}\\\phantom{-(x^4+)}2x^3+0\\\phantom{(x^4(}-\underline{(2x^3+4x^2)}\\\phantom{(x^4+4x^3+}-4x^2+2x\\\phantom{(x^4+4x}-\underline{(-4x^2-8x)}\\\phantom{(-x^4+4x^3+0+2}10x-3\\\phantom{(x^4+4x^3+0+}-\underline{(10x+20)}\\\phantom{-(x^4+4x^3+0+2x-3)}-23 \ \ \ \ \ \ \ \ \ \leftarrow \text{Rest}\end{array}$
Es gilt also:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

5

Berechne die Nullstellen folgender Funktionen mithilfe der Polynomdivision.

$f(x)=x^3-x^2-4x+4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

$f(x)=x^3-x^2-4x+4$

Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $1$ in $f(x)$ ein.

$f(1)=1^3-1^2-4\cdot1+4=0$

Die Funktion $f(x)$ hat an der Stelle $x_1=1$ eine Nullstelle. Da $f(1)=0$ , wissen wir, dass $f(x)$ den dazugehörigen Linearfaktor $(x-1)$ besitzt.

Führe nun die Polynomdivision $f(x):(x-1)$ durch.

$\def\arraystretch{1.25} \begin{array}{}\;\;\;(x^3-x^2-4x+4):(x-1)=x^2-4\\\underline{-(x^3-x^2)\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;0-4x+4\\\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(-4x+4)\;\;\;\;}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$

Die Funktion $f(x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_1=1$ bereits bekannt ist, kannst du die weiteren Nullstellen von $f$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.

$\displaystyle x^2-4$	$=$	$\displaystyle 0$	$\displaystyle +4$
$\displaystyle x^2$	$=$	$\displaystyle 4$
	↓	Wurzel ziehen.
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \pm\sqrt{4}$
	$=$	$\displaystyle \pm2$

Die Funktion $f(x)$ hat drei Nullstellen bei $x_1=1$ , $x_2=2$ und $x_3=-2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$g(x)=x^3+3x^2-16x+12$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

$g(x)=x^3+3x^2−16x+12$

Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $1$ in $g(x)$ ein.

$g(1)=1^3+3\cdot1^2-16\cdot1+12=0$

Die Funktion $g(x)$ hat an der Stelle $x_1=1$ eine Nullstelle. Da $g(1)=0$ , wissen wir, dass $g(x)$ den dazugehörigen Linearfaktor $(x-1)$ besitzt.

Führe nun die Polynomdivision $g(x):(x-1)$ durch.

$\def\arraystretch{1.25} \begin{array}{}{-}\;\;(x^3+3x^2-16x+12):(x-1)=x^2+4x-12\\\underline{-(x^3-x^2)\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;4x^2-16x\\\;\;\;\;\;\;\;\;\underline{-(4x^2-4x)\;\;\;\;}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-12x+12\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(-12x+12)}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$

Die Funktion $g(x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_1=1$ bereits bekannt ist, kannst du die weiteren Nullstellen von $g$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.

$\displaystyle x^2+4x-12$	$=$	$\displaystyle 0$
	↓	Mitternachtsformel anwenden.
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{-4\pm\sqrt{4^2-4\cdot1\cdot\left(-12\right)}}{2\cdot1}$
	↓	Unter der Wurzel zusammenfassen.
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{-4\pm\sqrt{64}}{2}$
	$=$	$\displaystyle \dfrac{-4\pm8}{2}$

$x_2=\dfrac{4}{2}=2$

$x_3=\dfrac{-12}{2}=-6$

Fall 1: $+$

Fall 2: $-$

Die Funktion $g(x)$ hat drei Nullstellen bei $x_1=1$ , $x_2=2$ und $x_3=-6$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$h(x)=3x^4+12x^3-33x^2-90x$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

$\displaystyle h\left(x\right)$	$=$	$\displaystyle 3x^4+12x^3-33x^2-90x$
	↓	$3x$ ausklammern.
$\displaystyle h\left(x\right)$	$=$	$\displaystyle 3x\cdot\left(x^3+4x^2-11x-30\right)$

$\Rightarrow x_1=0$

Die Funktion $h(x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_1=0$ bereits bekannt ist, kannst du die weiteren Nullstellen von $h$ bestimmen, indem du die Klammer gleich $0$ setzt.

$x^3+4x^2-11x-30=0$

Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $-2$ für $x$ ein.

$(-2)^3+4\cdot(-2)^2-11\cdot(-2)-30=-8+16+22-30=0$

Die Funktion $h(x)$ hat an der Stelle $x_2=-2$ eine Nullstelle. Da $h(-2)=0$ , wissen wir, dass $h(x)$ den dazugehörigen Linearfaktor $(x+2)$ besitzt.

Führe nun die Polynomdivision $(x^3+4x^2-11x-30):(x+2)$ durch.

$\def\arraystretch{1.25} \begin{array}{l}\phantom{-}\ (x^3+4x^2-11x-30):(x+2)=x^2+2x-15 \\-\underline{(x^3+ 2x^2)}\\\phantom{-(x^3-1}2x^2-11x\\\phantom{(x^3+}-\underline{(2x^2+4x)}\\\phantom{- (x^3+3x^2-}-15x-30\\\phantom{(x3+3x^2}-\underline{(-15x-30)}\\\phantom{-(x^3+3x^2-4x- 12}0\end{array}$

Setze das erhaltene Polynom gleich $0$ .

$\displaystyle x^2+2x-15$	$=$	$\displaystyle 0$
	↓	Mitternachtsformel anwenden.
$\displaystyle x_{3{,}4}$	$=$	$\displaystyle \dfrac{-2\pm\sqrt{2^2-4\cdot1\cdot\left(-15\right)}}{2\cdot1}$
	↓	Unter der Wurzel zusammenfassen.
$\displaystyle x_{3{,}4}$	$=$	$\displaystyle \dfrac{-2\pm\sqrt{64}}{2}$
$\displaystyle x_{3{,}4}$	$=$	$\displaystyle \dfrac{-2\pm8}{2}$

Fall 1: $+$

$x_3=\dfrac{6}{2}=3$

Fall 2: $-$

$x_4=\dfrac{-10}{2}=-5$

Die Funktion $h(x)$ hat vier Nullstellen bei $x_1=0$ , $x_2=-2$ , $x_3=3$ und $x_4=-5$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$i(x)=x^3-7x-6$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f(x)=0$ wird.

$\displaystyle i\left(x\right)$	$=$	$\displaystyle x^3-7x-6$
	↓	Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $1$ in $i(x)$ ein.
$\displaystyle i\left(1\right)$	$=$	$\displaystyle 1^3-7\cdot1-6$
$\displaystyle i\left(1\right)$	$=$	$\displaystyle -12$

$i(1)\neq0$

Setze z.B. $-1$ in $i(x)$ ein.

$i(-1)=(-1)^3-7\cdot(-1)-6=0$

Die Funktion $i(x)$ hat an der Stelle $x_1=-1$ eine Nullstelle. Da $i(-1)=0$ , wissen wir, dass $i(x)$ den dazugehörigen Linearfaktor $(x+1)$ besitzt.

Führe nun die Polynomdivision $i(x):(x+1)$ durch.

$\def\arraystretch{1.25} \begin{array}{}{-}\;\;(x^3+0x^2-7x-6):(x+1)=x^2-x-6\\\underline{-(x^3+x^2)\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;-x^2-7x\\\;\;\;\;\;\;\;\;\underline{-(-x^2-x)\;\;\;\;}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-6x-6\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(-6x-6)}\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$

Die Funktion $i(x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_1=-1$ bereits bekannt ist, kannst du die weiteren Nullstellen von $i$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.

$\displaystyle x^2-x-6$	$=$	$\displaystyle 0$
	↓	Mitternachtsformel anwenden.
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{1\pm\sqrt{\left(-1\right)^2-4\cdot1\cdot\left(-6\right)}}{2\cdot1}$
	↓	Unter der Wurzel zusammenfassen.
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{1\pm\sqrt{25}}{2}$
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{1\pm5}{2}$

$x_2=\dfrac62=3$

$x_3=\dfrac{-4}{2}=-2$

Fall 1: $+$

Fall 2: $-$

Die Funktion $i(x)$ hat drei Nullstellen bei $x_1=-1$ , $x_2=3$ und $x_3=-2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

6

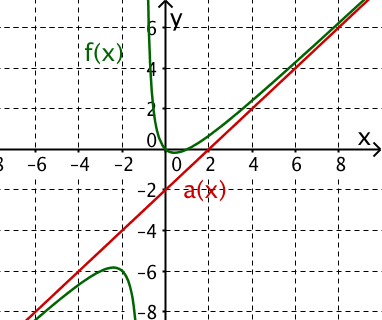
Zeige, dass die Polynomdivisionen dieser Aufgabengruppe nicht aufgehen. Gib für jede der zu den Polynomdivisionen gehörenden gebrochenrationalen Funktion deren asymptotisches Verhalten im Unendlichen an.

$(2x^2-x-2):(x-1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
$\def\arraystretch{1.25} \begin{array}{l}\;\;(2x^2-x-2):(x-1)=\displaystyle2x+1-\frac1{x-1}\\\color{red}{-} \underline{(2x^2-2x)\;\;\;\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;1x-2\\\;\;\;\;\;\;\;\;\;\;\;\color{red}{-}\underline{(1x-1)\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-1\;\;\;\;\color {red}{Rest}\end{array}$
Die Polynomdivision "geht nicht auf". Der verbleibende Rest $(-1)$ wird als Bruchterm mit dem Divisor als Nenner zum Teilergebnis des Divisionsverfahrens hinzugefügt.
Nun folgt die Asymptotenberechnung für $x \rightarrow \pm \infty$ .
Dem Quotient $(2x^2-x-2):(x-1)$ entspricht die gebrochenrationale Funktion
Die Polynomdivision hat f(x) in die Differenz aus dem Polynom ersten Grades $a(x)=2x+1$ und der echtgebrochenrationalen Funktion $r(x)$ zerlegt.
$f(x)=\underbrace{2x+1}_{\displaystyle \color {red}{a(x)}} -\underbrace {\frac{1}{x-1}}_{\displaystyle \color {red}{r(x)}}$
Bringe $a(x)$ auf die linke Seite der Gleichung.
$f(x)-a(x)= \displaystyle \frac{-1}{x-1}$
Für jede echtgebrochenrationale Funktion $r(x)$ gilt:
$\lim _{x\rightarrow \pm \infty }r(x)=0$
$f(x)-a(x)= \underbrace{\frac{-1}{x-1}}_{\displaystyle \color{red}{\rightarrow 0} \;\text{falls}\; x\rightarrow \pm \infty}$
Damit unterscheiden sich $f(x)$ und $a(x)$ für $x$ gegen plus/minus Unendlich um beliebig wenig.
Die Gerade $a(x)=2x+1$ ist deshalb die Asymptote von $f(x)$ für $x$ gegen plus/minus Unendlich.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^2-x):(x+1)$

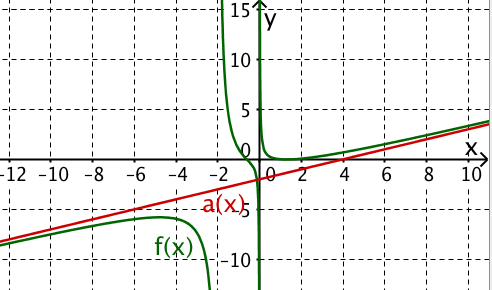
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
$\def\arraystretch{1.25} \begin{array}{l}\;\;(x^2-x):(x+1)=x-2+\displaystyle\frac2{x-1}\\\color{red}{-}\underline{(x^2+x)\;\;\;}\\\;\;\;\;\;-2x+0\\\;\;\;\;\,\color{red}{-}\underline{(2x-2)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,2\;\;\;\;\color{red}{Rest}\end{array}$
Die Polynomdivision "geht nicht auf". Der verbleibende Rest wird als Bruchterm mit dem Divisor als Nenner dem Teilergebnis hinzugefügt.
Nun folgt die Asymptotenberechnung für $x\rightarrow \pm\infty$ .
Dem Quotienten $(x^2-x):(x+1)$ entspricht die gebrochenrationale Funktion
Die Polynomdivision hat $f(x)$ in die Summe aus der linearen Funktion $a(x)$ und die echtgebrochenrationale Funktion $r(x)$ zerlegt.
Bringe $a(x)$ auf die linke Seite der Gleichung.
Für jede echtgebrochenrationale Funktion $r(x)$ gilt
Damit unterscheidet sich $f(x)$ von $a(x)$ für $x$ gegen plus/minus Unendlich um beliebig wenig.
Die Gerade $a(x)=x-2$ ist somit die Asymptote von $f(x)$ für $x$ gegen plus/minus Unendlich.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(x^3-2x^2+1):(2x^2+4x)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
$\def\arraystretch{1.25} \begin{array}{l}\;\;(x^3-2x^2+1):(2x^2+4x)=\displaystyle\frac{1}{2}x-2+\frac{8x+1}{2x^2+4x}\\\underline{\color{red}{-}(x^3+2x^2)\;\;\;}\\\;\;\;\;\;\;-4x^2+1\\\;\;\;\underline{\color{red}{-}(-4x^2-8x)\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;+8x+1\;\;\;\;\color{red}{Restpolynom}\end{array}$
Die Polynomdivision "geht nicht auf".
Der Grad des verbleibenden Restpolynoms des Dividenden ist kleiner als der Grad des Divisors und es wird als Bruchterm mit dem Divisor als Nenner zum Teilergebnis des Divisionsverfahrens hinzugefügt
Nun folgt die Asymptotenberechnung für $x\rightarrow \pm \infty$ .
Dem Quotienten $(x^3-2x^2+1):(2x^2+4x)$ entspricht die gebrochenrationale Funktion
Die Polynomdivision hat $f(x)$ in die Summe der linearen Funktion $a(x)$ und eine echtgebrochenrationale Funktion $r(x)$ zerlegt.
Bringe $a(x)$ auf die linke Seite der Gleichung.
Für jede echtgebrochenrationale Funktion $r(x)$ gilt
Damit unterscheidet sich $f(x)$ von $a(x)$ für $x$ gegen plus/minus Unendlich um beliebig wenig.
Die Gerade $a(x)=0{,}5x-2$ ist somit die Asymptote der Funktion $f(x)$ für $x$ gegen plus/minus Unendlich.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Vorbereitung der Polynomdivision:
Ordne sowohl das Polynom des Dividenden als auch das Polynom des Divisors nach fallenden Potenzen.
$(1-x^4):(1+x+x^2)=$
$(-x^4+1):(x^2+x+1)$
Polynomdivision:
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-}(-x^4+1):(x^2+x+1)=\displaystyle{-x^2+x+\frac{1-x}{x^2+x+1}}\\\color{red}{-(}\underline{-x^4-x^3-x^2\color{red}{)}}\\\hphantom{(-x^4+1}x^3+x^2+1\\\hphantom{-(x^4+}\color{red}{-(}\underline{x^3+x^2+x}\color{red}{)}\\\hphantom{-(x^4+1)=-x}-x+1\;\;\;\;\color{red}{Rest}\end{array}$
ausführliche Polynomdivision mit den fehlenden Gliedern im Dividenden
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-}(-x^4+\color{red}{0}\cdot x^3+\color{red}{0}\cdot x^2+\color{red}{0}\cdot x+1):(x^2+x+1)=\displaystyle{-x^2+x+\frac{1-x}{x^2+x+1}}\\\color{red}{-(}\underline{-x^4-\color{red}{1}\cdot x^3-\color{red}{1}\cdot x^2}\color{red}{)}\\\hphantom{-((x^3(} \color{red}{+1}\cdot x^3\color{red}{+1} \cdot x^2+\color{red}{0} \cdot x\\\hphantom{{-}-((}\color{red}{-(}\underline{\;\;\;\;\,x^3+\;\;\;\;\,x^2+\;\;\;\,x\color{red}{)}}\\\hphantom{-(x^3-(+x^3+x^3+x^3+\,} -x+1\end{array}$
Nun folgt die Asymptotenberechnung für $x\rightarrow\pm\infty$ .
Dem Quotienten $(-x^4+1):(x^2+x+1)$ entspricht die gebrochenrationale Funktion
.
Die Polynomdivision hat $f(x)$ in die Summe aus dem Polynom 2. Grades $a(x)=-x^2+x$ und die echt gebrochenrationale Funktion r(x) mit dem Zählergrad 1 und dem Nennergrad 2 zerlegt.
$\displaystyle f(x) =\underbrace{-x^2+x}_{\displaystyle \color{red}{a(x)}}+\underbrace{\frac{1-x}{x^2+x+1}}_{\displaystyle \color{red}{r(x)}}$
Bringe $a(x)$ auf die linke Seite der Gleichung.
$f(x)-a(x)= \displaystyle \frac{1-x}{x^2+x+1}$
Für jede echtgebrochenrationale Funktion $r(x)$ gilt:
$\lim_{x \rightarrow \pm \infty}r(x)=0$
$\displaystyle f(x)-a(x)= \underbrace{\frac{1-x}{x^2+x+1}}_{\displaystyle \color{red}{\rightarrow 0} \;\text{falls}\; x\rightarrow \pm \infty}$
Damit unterscheiden sich $f(x)$ und $a(x)$ für x gegen plus/minus Unendlich um beliebig wenig.
Die nach unten geöffnete Parabel $a(x)$ ergibt die asymptotische Kurve von $f(x)$ für x gegen plus/minus Unendlich.
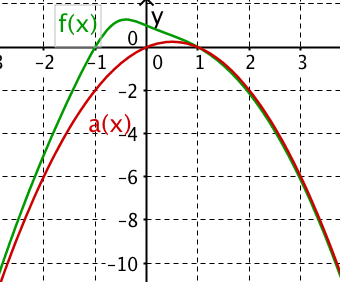
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

7

Tintenkleckse

Was verbirgt sich dahinter?

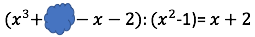
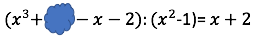
Setze a für den gesuchten Klecks und starte mit der Multiplikationsprobe der Division
$\def\arraystretch{1.25} \begin{array}{lcl}(x+2)\cdot(x^2-1) &=& x^3+a-x-2\\x^3-x+2x^2-2&=&x^3+a-x-2\\a&=&2x^2 \end{array}$
Löse die Gleichung nach $a$ auf.
Der Tintenklecks verdeckt den Term $2x^2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
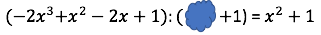
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
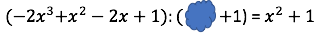
Setze $a$ für den gesuchten Klecks und starte mit der Multiplikationsprobe der Division:
$\def\arraystretch{1.25} \begin{array}{lcl}(x^2+1)\cdot(a+1) &=& -2x^3+x^2-2x+1\\ax^2+x^2+a+1 &=& -2x^3+x^2-2x+1\\a(x^2+1) &=&-2x^3-2x\\a(x^2+1) &=&-2x(x^2+1)\\a &=&-2x\end{array}$
Löse die Gleichung nach a auf.
Der Tintenklecks verdeckt den Term $-2x$ .
Alternative Lösung über die Polynomdivision
$(-2x^3+x^2-2x+1):(a+1)=x^2+1$
Starte die Polynomdivision
Schon der erste Schriit des Verfahrens der Polynomdivision ergibt einen Wert für $a$ :
$\def\arraystretch{1.25} \begin{array}{lcl} -2x^3:a &=& x^2\;\;\;\;\;\;\;|\cdot a \\-2x^3 &=&a\cdot x^2\;\;\;|:x^2\\\Rightarrow a &=&-2x\end{array}$
Es ist allerdings noch nachzurechnen, dass die Polynomdivision mit diesem Wert für $a$ auch wirklich aufgeht.
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-} (-2x^3+x^2-2x+1):(\color{red}{-2x}+1)=x^2+1\\ \color{red}{-} (\underline{-2x^3+x^2})\\\hphantom{-(2x^3+x+1}-2x+1\\\hphantom{-2x^3+x^2}\;\,\color{red}{-}\underline{(-2x+1)}\\\hphantom{(-2x^3+x^2-2x+1+}\color{red}{0}\end{array}$
Die Polynomdivision geht also mit $a=-2x$ tatsächlich auf. Der Tintenklecks ist entzaubert!
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
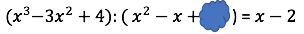
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
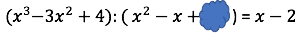
Setze $a$ für den gesuchten Klecks ein und starte mit der Multiplikationsprobe der Division.
$\def\arraystretch{1.25} \begin{array}{lcl} (x-2)\cdot(x^2-x+a)&=&x^3-3x^2+4 \\ x^3-x^2+ax-2x^2+2x-2a &=& x^3-3x^2+4\\ x^3-3x^2+2x+a(x-2) &=&x^3-3x^2+4\\ a(x-2) &=&4-2x\\ a(x-2) &=&-2(x-2)\;\;\;\;\;\;|:(x-2)\\ a&=&-2 \end{array}$
Löse die Gleichung nach $a$ auf.
Der Tintenklecks verdeckt die Zahl $-2$ .
Alternative Lösung über die Polynomdivision
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{\-} (x^3-3x^2\;\;\;\;\;\;+4)\cdot(x^2-x+a)=x-2\\\color{red}{-}\underline{(x^3-\;x^2+ax)}\\\hphantom{-x^3} -2x^2-ax+4\\\hphantom{-}\color{red}{-}\underline{(-2x^2+2x-2a)}\\\hphantom{-x\; } -(\underbrace{a+2}_{\color{red}{\displaystyle 0\text{!}}})x +(\underbrace{4+2a}_{\color{red}{\displaystyle0\text{!}}})\end{array}$
Die Polynomdivision geht genau für $a=-2$ auf.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

8

Polynomdivisionen mit Parametern

Führe die Polynomdivisionen durch. Faktorisiere anschließend das Polynom des Dividenden durch Bestimmung all seiner Nullstellen.

$(x^3+(3-a)x^2+(2-3a)x-2a):(x+2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Das Polynom des Dividenden ist vom Grade 3 und nach fallenden Potenzen geordnet und somit für das Divisionsverfahren geeignet. Die Koeffizienten beim quadratischen und beim linearen Glied sind in Klammern stehende Differenzen mit einem Parameter a.
$\def\arraystretch{1.25} \begin{array} {l} \phantom{-} (x^3+(3-a)x^2+(2-3a)x-2a):(x+2)=x^2+(1-a)x-a \\\color {red}{-}(\underline{x^3+\;\;\;\;\;\;\;2x^2}) \\\phantom {-(x^3+}\;(1-a)x^2+(2-3a)x \\\phantom{(x+}\color {red} {-}(\underline{(1-a)x^2+(2-2a)x})\\\phantom {-(x^3+(3-a)x^2+(2} \;\;-ax-2a\\\phantom {-(x^3+(3-)\;x^2+(2}\color {red}{-}(\underline{-ax-\;2a})\\\phantom {-(x^3+(3-a)x^2+(2-3a)x)x-}\color{red}0\end{array}$
Da die Division des Polynom 3.Grades durch $(x+2)$ aufgegangen ist, hat es $x_1=-2$ als 1. Nullstelle.
Die eventuellen Nullstellen des Ergebnispolynoms $x^2+(1-a)x-a$ sind dann seine weiteren Nullstellen.
Nullstellenberechnung
$x^2+(1-a)x-a=0$
Berechne die Lösungen der quadratischen Gleichung mit der Mitternachtsformel.
$x_{2/3}=\displaystyle \frac{-(1-a)\pm\sqrt{(1-a)^2-4\cdot1\cdot(-a)}}{1\cdot2}$
$x_{2/3}=\displaystyle \frac{(-1+a)\pm\sqrt{1-2a+a^2+4a}}2$
$x_{2/3}=\displaystyle\frac{(-1+a)\pm\sqrt{1+2a+a^2}}2$
$x_{2/3}=\displaystyle\frac{(-1+a)\pm\sqrt{(1+a)^2}}2$
$x_{2/3}=\displaystyle\frac{(-1+a)\pm(1+a)}2$
$x_2=a \wedge x_3=-1$
Alle Nullstellen des Polynoms 3. Grades sind: -1, -2, a
Faktorisierung
Für das gegebene Polynom 3. Grades $x^3+(3-a)x^2+(2-3a)x-2a$ ergibt sich somit folgende Linearfaktorzerlegung:
$(x^3+(3-a)x^2+(2-3a)x-2a)=(x-a)(x+2)(x+1)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$(-x^3+x^2+\mathrm{ex}^2-\mathrm{ex}+2x-2e):(x-2)$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Vorbereitung der Polynomdivision
Bevor man mit einer Polynomdivision beginnt, muss man
sicherstellen, dass sowohl im Dividenden als auch im Divisor die Polynome nach fallenden Exponenten geordnet sind und
sollte man Glieder mit gleichem Exponenten zusammenfassen.
Dies erreicht man durch eventuelles Umstellen von Gliedern und durch Ausklammern.
Beide Polynome sind hier bereits nach fallenden Potenzen geordnet. Sowohl das Polynom 3. Grades des Dividenden, als auch das Polynom 1. Grades des Divisors. Die quadratischen und die linearen Glieder des Dividendenpolynoms sind aber noch nicht zusammengefasst.
$-x^3+\color{red}{\underbrace{x^2+ex^2}_{\displaystyle(1+e)x^2}}-\color{red}{\underbrace{ex+2x}_{\displaystyle(e-2)x}} -2e$
Fasse im Dividenden die quadratischen und die linearen Glieder durch Ausklammern zusammen.
Polynomdivision
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-} (-x^3+(1+e)x^2-(e-2)x-2e):(x-2)=-x^2+(e-1)x+e\\\color{red}{-}\underline{(-x^3\;\;\;\;\;\;\,\,+2x^2})\\\hphantom{(-x^3+(1}\color{red}{(e-1)}x^2-(e-2)x\\\hphantom{-(-x^3}\color{red}{-}\underline{[(e-1)x^2-2(e-1)x}]\\\hphantom{-(x^3+(1+e)x^2-(e-2)x-}\color{red}{e}x-2e\\\hphantom{-(x^3+(1+e)x^2-(e-2}\color{red}{-}(\underline{ex-2e})\\\hphantom{-(x^3+(1+e)x^2-(e-2)x-2e}0\end{array}$
alternative Polynomdivision (ohne Zusammenfassen im Dividendenpolynom)
$\def\arraystretch{1.25} \begin{array}{}[l]\;\;\;(-x^3+x^2+ex^2-ex+2x-2e):(x-2)=-x^2+(-x+ex)+e\\\underline{-(-x^3+2x^2)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-x^2+ex^2-ex+2x\\\;\;\;\;\;\;\;\;\;\;\;\;\underline{(-x^2+ex^2-2ex+2x)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;ex-2e\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-(ex-2e)}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$
Nullstellenberechnung
$-x^2+(e-1)x+e=0$
Löse die quadratische Gleichung mit der Mitternachtsformel
$x_{2;3}=\displaystyle\frac{-(e-1)\pm\sqrt{(e-1)^2-4\cdot(-1)\cdot e}}{-2}$
Das Minus in Nenner und Zähler kürzt sich weg.
$x_{2;3}=\displaystyle\frac{(e-1)\pm\sqrt{e^2-2e+1+4e}}2$
Unter der Wurzel zusammenfassen
$x_{2;3}=\displaystyle\frac{(e-1)\pm\sqrt{e^2+2e+1}}2$
Auf die Diskriminante unter der Wurzel kann die erste Binomische Formel angewendet werden.
$x_{2;3}=\displaystyle\frac{(e-1)\pm\sqrt{(e+1)^2}}2$
Wurzelziehen
$x_{2;3}=\displaystyle\frac{(e-1)\pm(e+1)}2$
$x_2=e \wedge x_3=-1$
Faktorisierung
Für das gegebene Polynom 3. Grades $-x^3+x^2+ex^2-ex+2x-2e$ ergibt sich somit folgende Linearfaktorzerlegung: $-(x+1)(x-2)(x-e)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

9

Ausgefallene Polynomdivisionen

Berechne:
$(x^4+\sqrt{3}x^2+1):(x^2-1)$

Polynomdivision
Benutze das Verfahren der Polynomdivision um die Aufgabe zu lösen.
Die Koeffizienten der Polynome müssen nicht ganzzahlig sein. Es können auch Brüche oder gar irrationale Zahlen vorkommen. Das Verfahren der Polynomdivision wird dadurch nicht beeinflusst. Lediglich einzelne Rechenschritte gestalten sich teilweise unangenehmer.
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-} \displaystyle(x^4+\sqrt{3}x^2+1):(x^2-1)={x^2+(\sqrt{3}+1)+\frac{\sqrt{3}+2}{ x^2-1}}\\-(\underline{x^4\;\,\;\;-x^2})\\\;\;\;(\sqrt{3}+1)x^2\;+1\\-[\underline{(\sqrt{3}+1)x^2-(\sqrt{3}+1)]}\\\hphantom{-(x^4+3+x^2+1}\sqrt{3}+2\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne:
$(2x^4+x^2-x-1):(x^2-1):(x^2+1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Polynomdivision
So wie die Aufgabe gestellt ist, hat man zwei Polynomdivisionen nacheinander durchzuführen. Dies kann man vermeiden und kommt mit einer Polynomdivision aus, wenn man die folgende Rechenregel für Divisionen anwendet:
Führe die Polynomdivision durch.
Überprüfe, ob du zum gleichen Endergebnis kommst, wenn du - wie in der Aufgabenstellung - beide Divisionen nacheinander durchführst.
Die erste Division:
$\def\arraystretch{1.25} \begin{array} {l}\hphantom{-}(2x^4+\;\;x^2-x-1):(x^2-1)=2x^2+3+\displaystyle\frac{-x+2}{x^2-1}\\\color{red}{-}(\underline{2x^4-2x^2})\\\hphantom{(2x^4+xy}3x^2-x-1\\\hphantom{(2x^4x}\color{red}{-}(\underline{3x^2\;\;\;\;\;\;-3})\\\hphantom{(2x^4+x^2)+}\;-x+2\;\;\;\;\;\color{red}{Rest}\end{array}$
Die anschließende zweite und aufwändige Division:
$\def\arraystretch{1.25} \begin{array}{l l}\;\displaystyle\left(2x^2+3+\frac{-x+2}{x^2-1}\right):\left(x^2+1\right)&=2+\displaystyle\frac{\left(1+\displaystyle\frac{-x+2}{x^2-1}\right)}{x^2+1}\\\color{red}{-}(\underline{2x^2+2})\\\hphantom{(2x^2+3}\;\color{red}{1+\displaystyle\frac{-x+2}{x^2+1}\;\;Rest}\\&=2+\displaystyle\frac{\displaystyle\frac{x^2-1-x+2}{x^2-1}}{x^2+1}\\&=2+\displaystyle\frac{x^2-x+1}{(x^2-1)(x^2+1)}\\&=2+\displaystyle\frac{x^2-x+1}{x^4-1}\end{array}$
Die "doppelte" Polynomdivision führt am Ende zum gleichen Ergebnis.
Die Zweckmäßigkeit des geschickten Verwendens der Rechenregel
ist aber ersichtlich.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne:
$(3x^3+3x^2-4x-4):(\sqrt{3}x-2):(\sqrt{3}x+2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Polynomdivision
$(3x^3+3x^2-4x-4):(\sqrt{3}x-2):(\sqrt{3}x+2)$
Benutze die Rechenregel
um mit einer Polynomdivision auszukommen.
Verwende den Divisor $3x^2-4$ für die Polynomdivision und führe die Polynomdivision durch.
$\hphantom{-}(3x^3+3x^2-4x-4):(3x^2-4)=x+1\\\color{red}{-}(\underline{3x^3\;\;\;\;\;\;\,\;\;-4x})\\\hphantom{-(3x^3+\;}3x^2\;\;\;\;\;\;\;-4\\\hphantom{-(3x^3}\color{red}{-}(\underline{3x^2\;\;\;\;\;\;\,-4})\\\hphantom{-3x^3+3x^2-4x-4} 0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\displaystyle f\left(x\right)$	$=$	$\displaystyle 4x^2-4x$
	↓	Gleich $0$ setzen.
$\displaystyle 0$	$=$	$\displaystyle 4x^2-4x+0$
	↓	Mitternachtsformel anwenden.
$\displaystyle x_{2{,}3}$	$=$	$\displaystyle \dfrac{4\pm\sqrt{\left(-4\right)^2-4\cdot4\cdot0}}{2\cdot4}$
	$=$	$\displaystyle \dfrac{4\pm\sqrt{16}}{8}$
	$=$	$\displaystyle \dfrac{4\pm4}{8}$

$\displaystyle x^2+1$	$=$	$\displaystyle 0$	$\displaystyle -1$
$\displaystyle x^2$	$=$	$\displaystyle -1$

Verbleibende Nullstellen berechnen

Faktorisierung

Hast du eine Frage oder Feedback?

Verbleibende Nullstellen berechnen

Faktorisierung

Hast du eine Frage oder Feedback?

Nullstellenberechnung

Hast du eine Frage oder Feedback?

Verbleibende Nullstellen berechnen

Hast du eine Frage oder Feedback?

Schnittpunkte berechnen

Polynomdivision

Verbleibende Nullstellen berechnen

weitere Schnittpunkte berechnen

Schnittpunkte

Durchführung der Zahlendivision

Durchführung der Polynomdivision

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösen mit Polynomdivision

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nullstellenberechnung

Faktorisierung

Hast du eine Frage oder Feedback?

Polynomdivision

Nullstellenberechnung

Faktorisierung

Hast du eine Frage oder Feedback?

Polynomdivision

Hast du eine Frage oder Feedback?

Polynomdivision

Hast du eine Frage oder Feedback?

Polynomdivision

Hast du eine Frage oder Feedback?