Aufgaben zum Sinus, Kosinus und Tangens im rechtwinkligen Dreieck
- 1
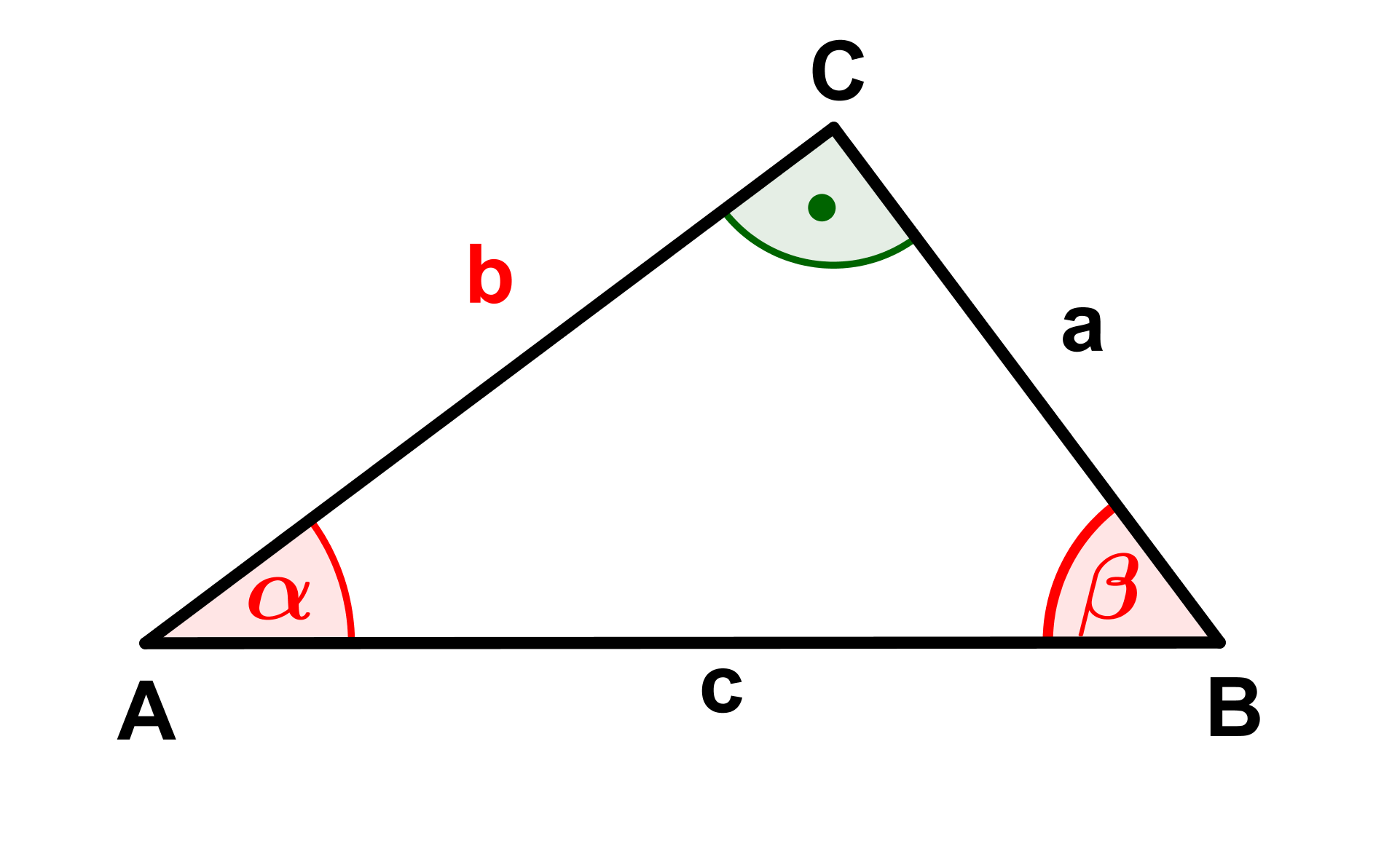
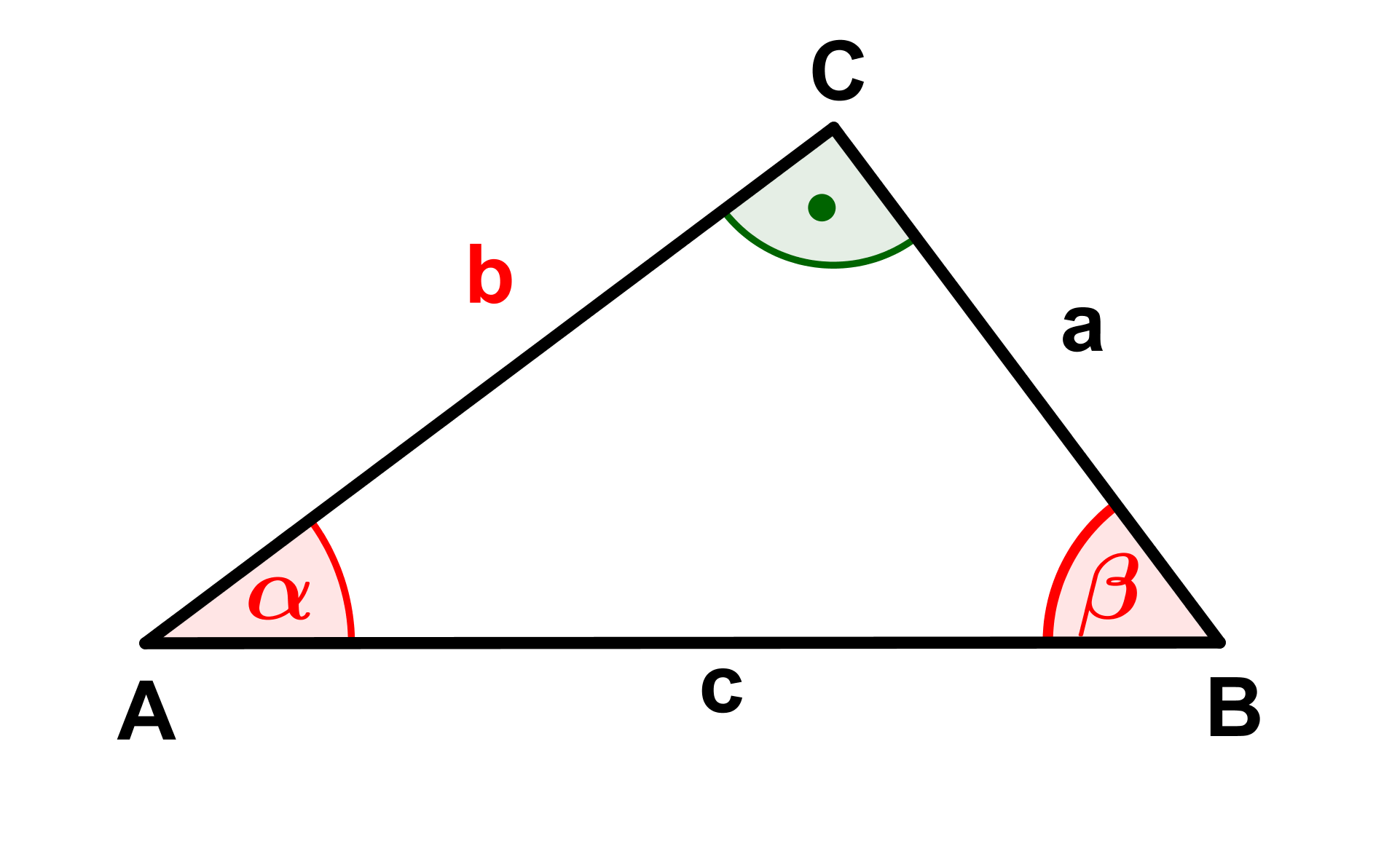
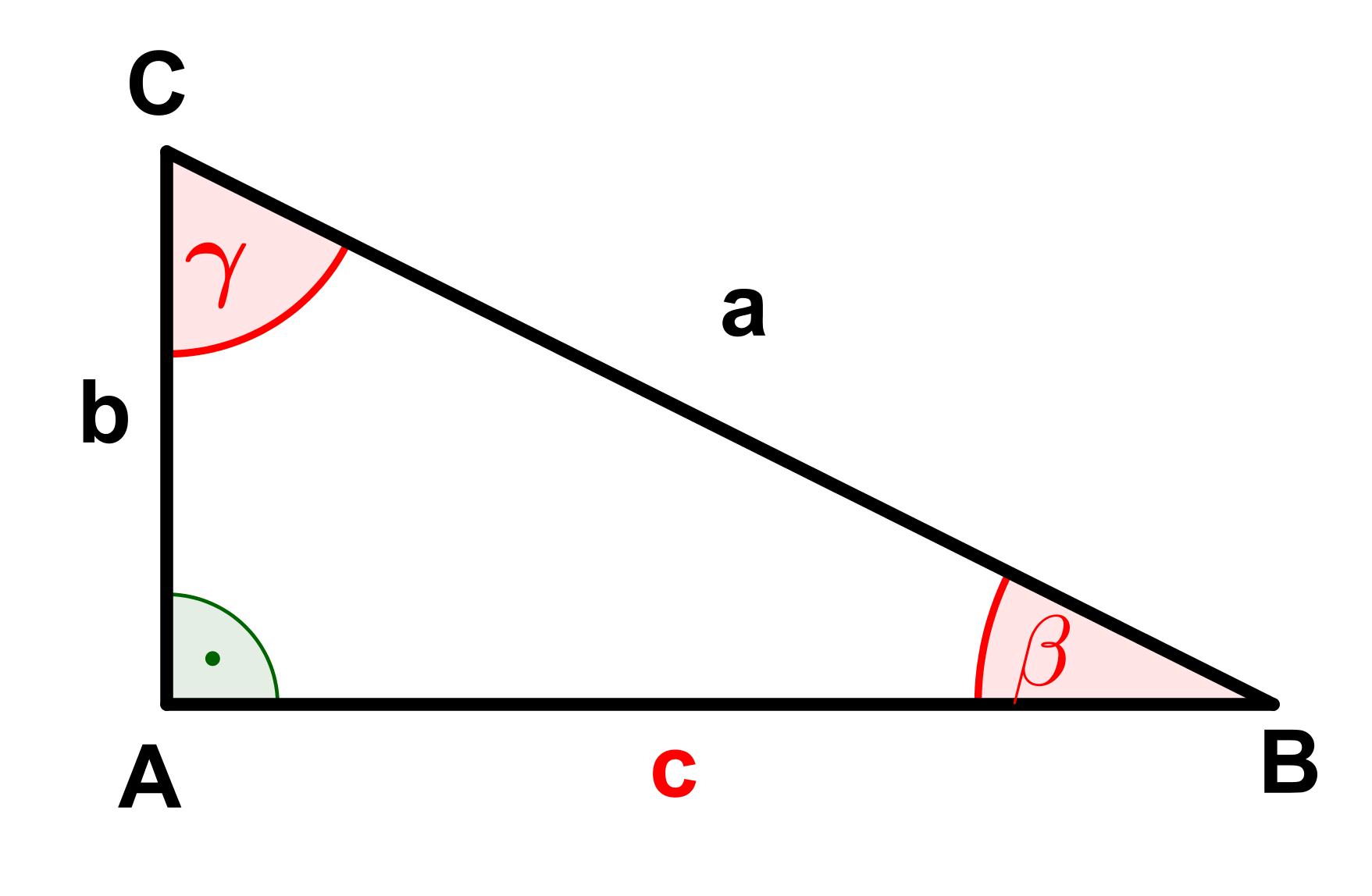
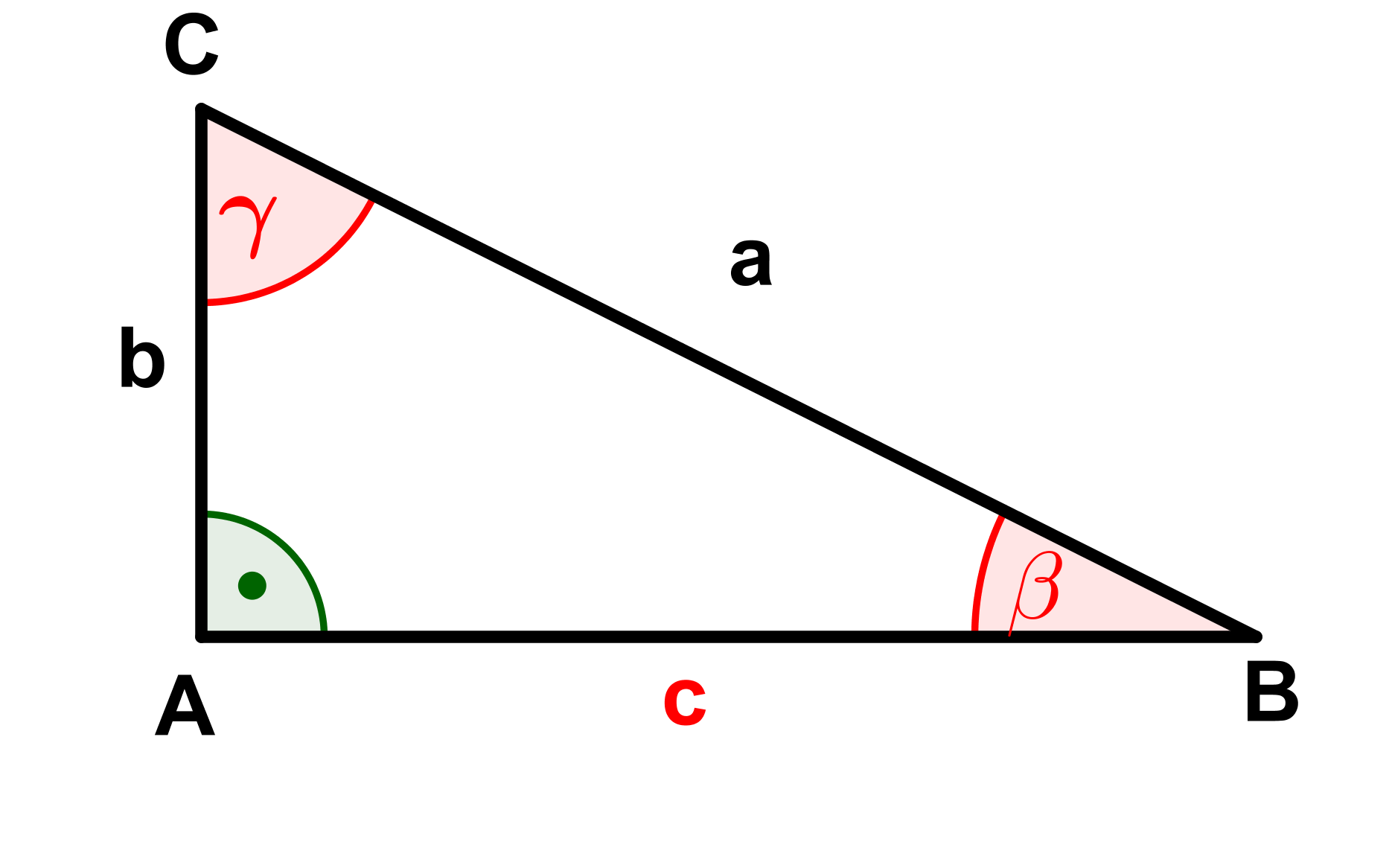
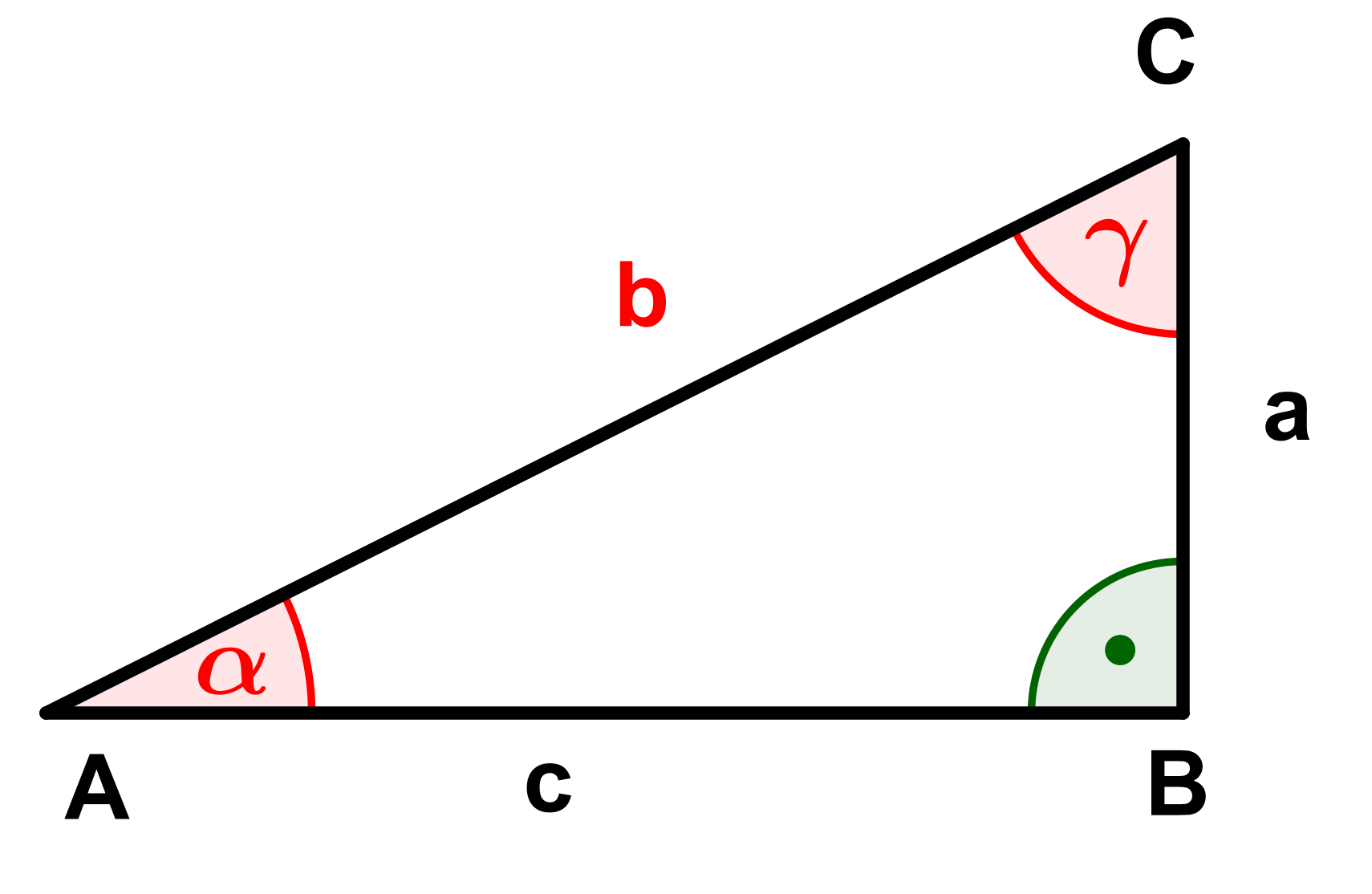
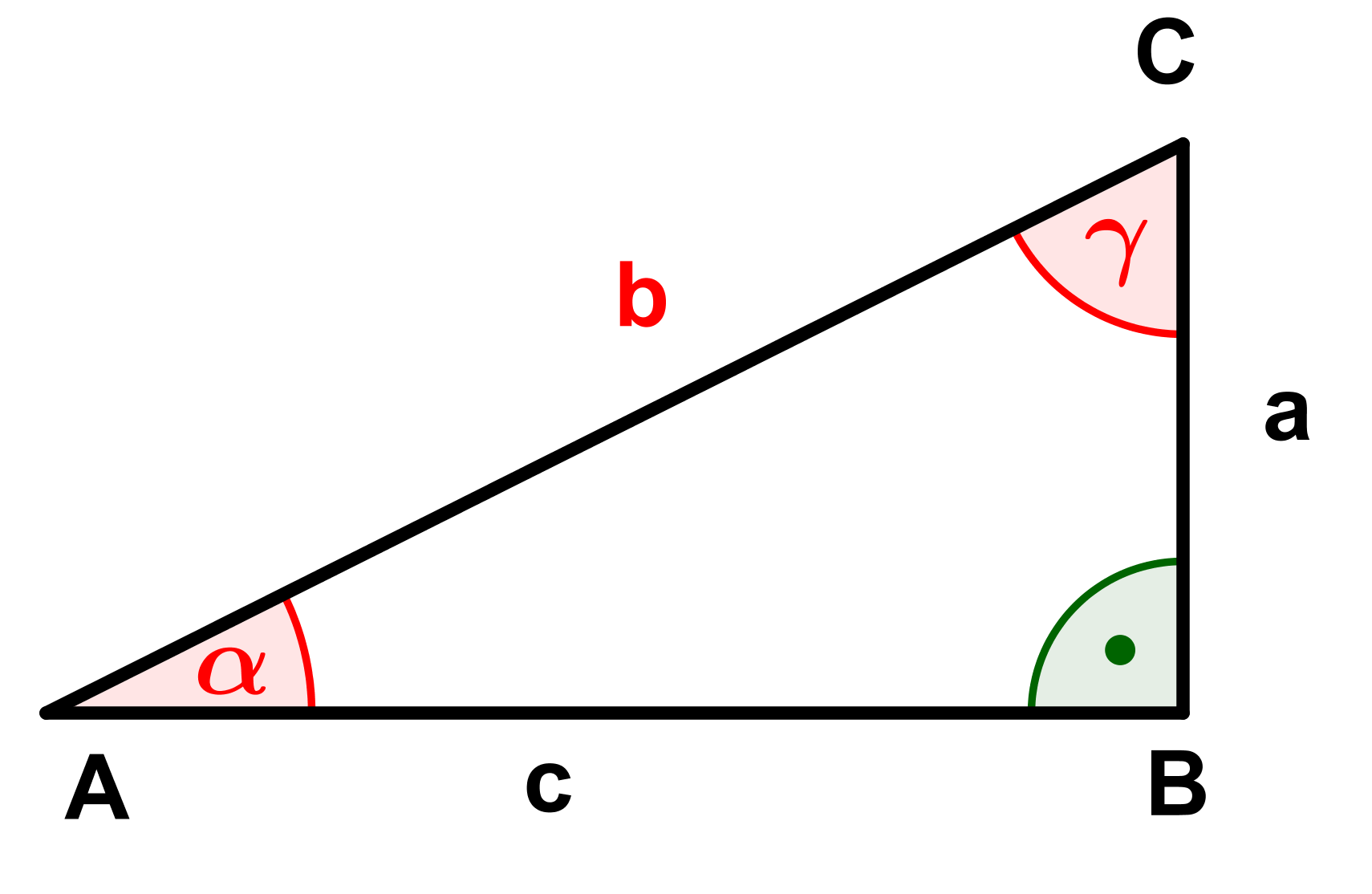
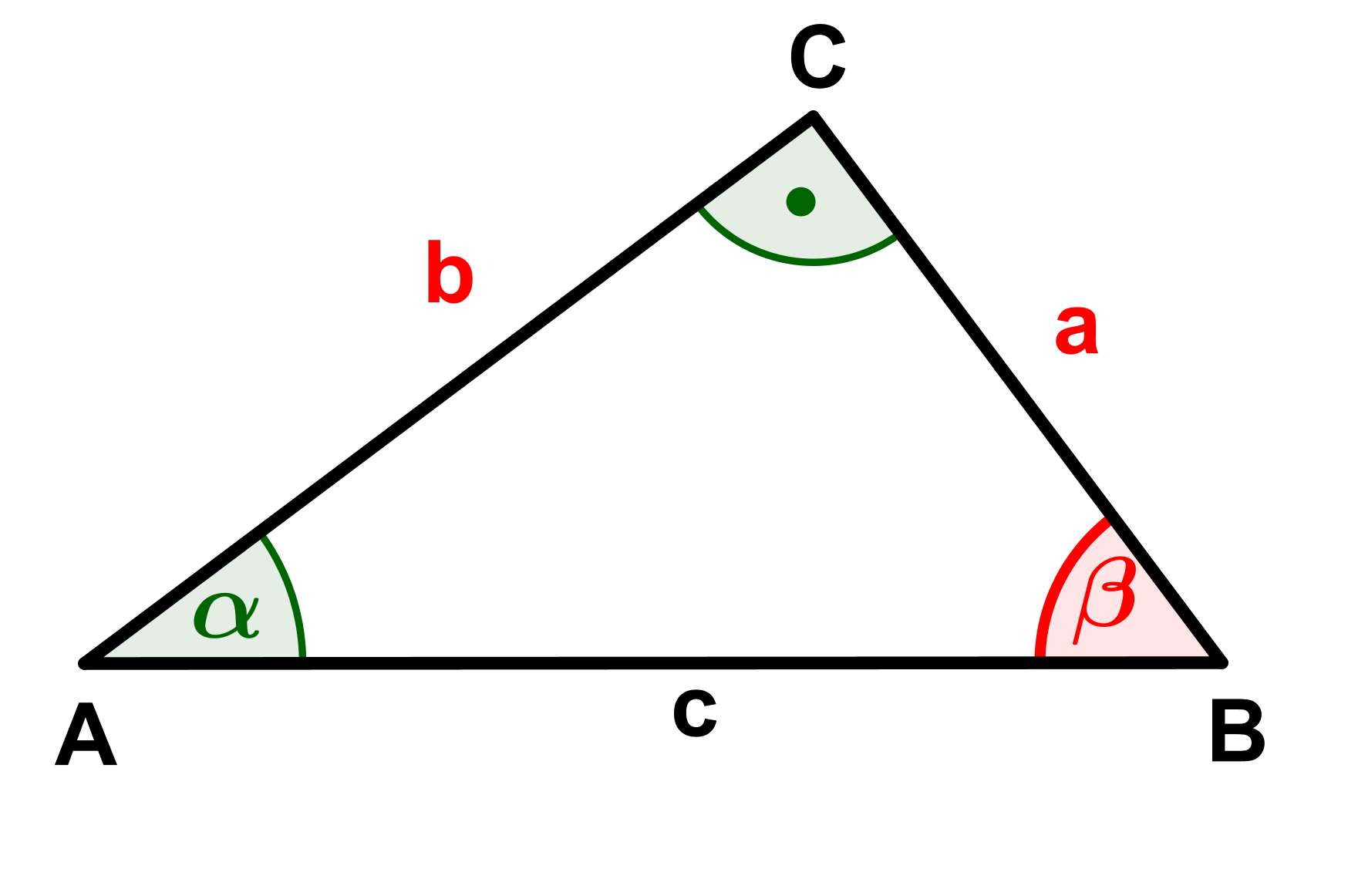
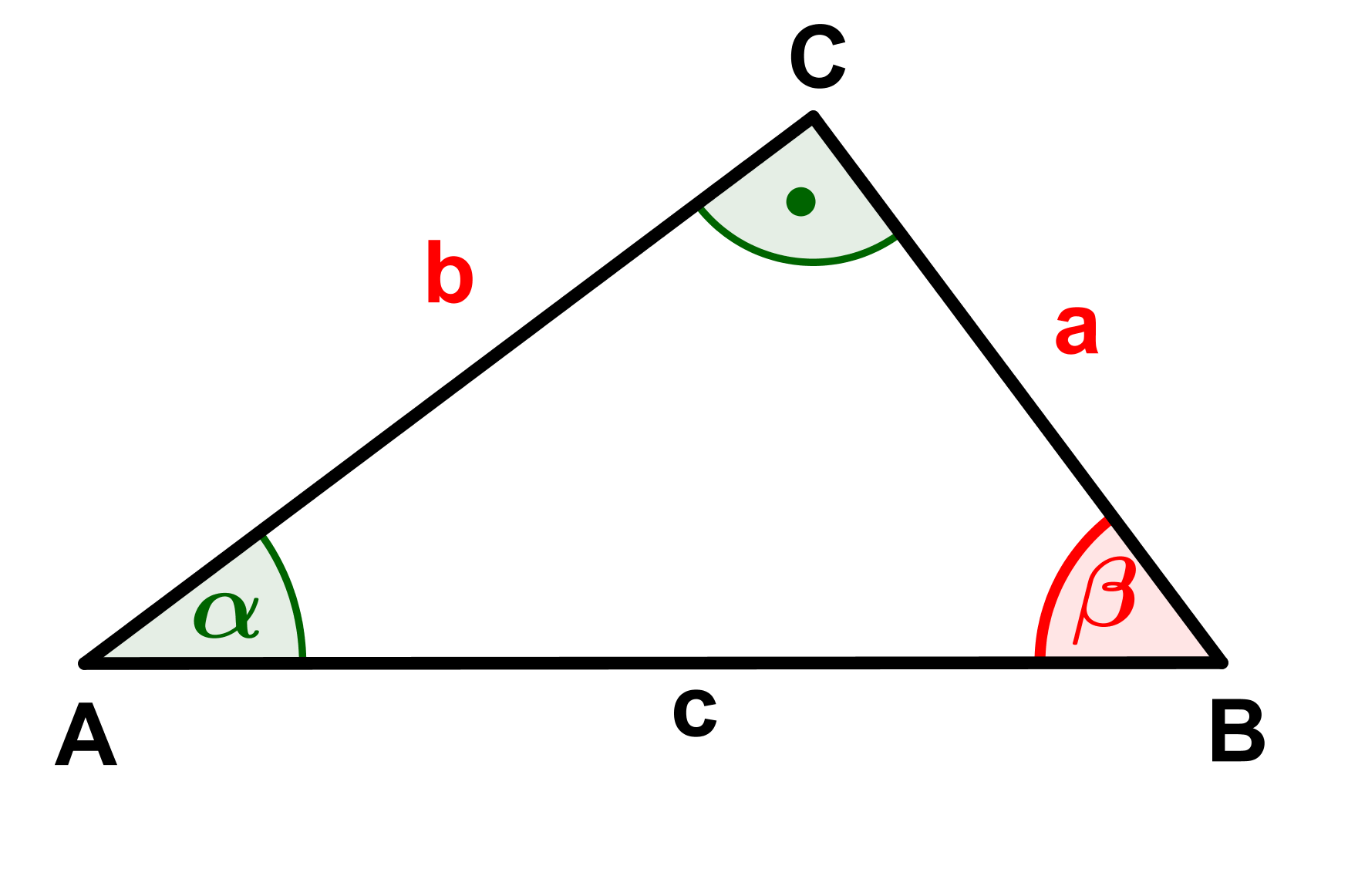
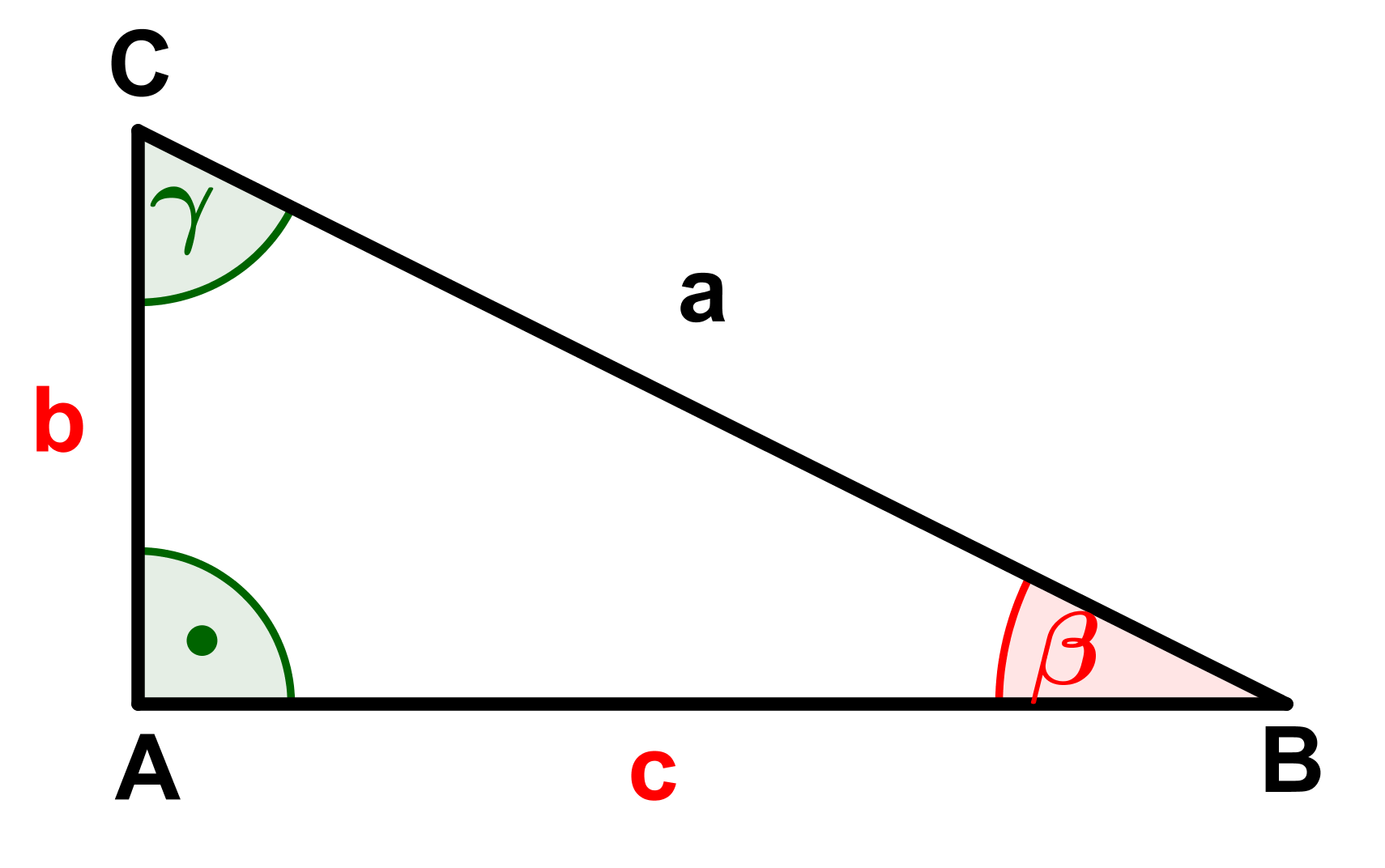
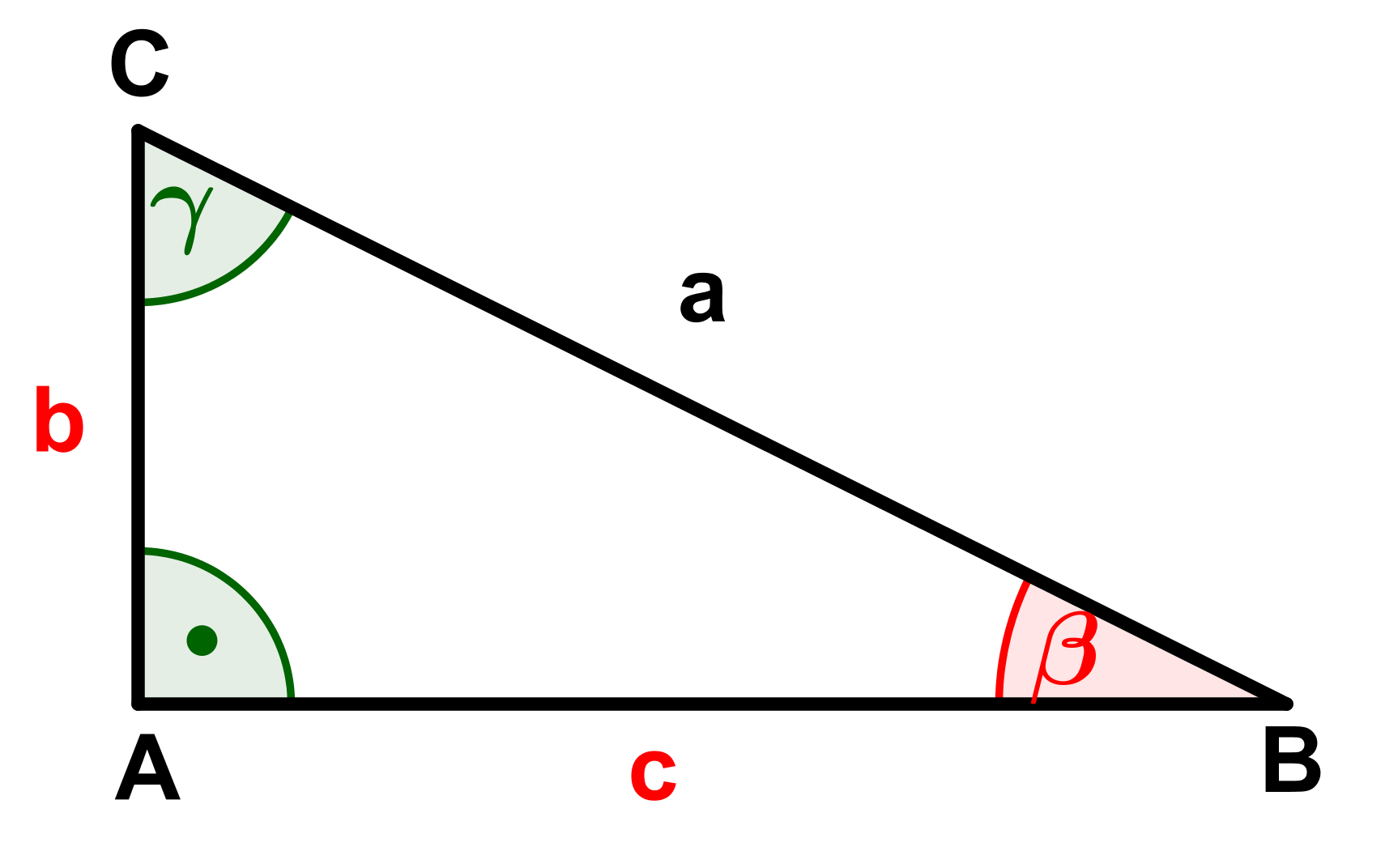
Berechne die fehlenden Seiten und Winkel (rot markiert) der Dreiecke.
- 2
Berechne in einem rechtwinkligen Dreieck mit und die Seitenlänge von . Runde auf zwei Nachkommastellen.
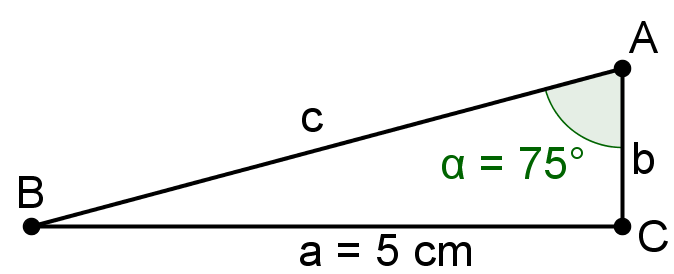 cm
cm - 3
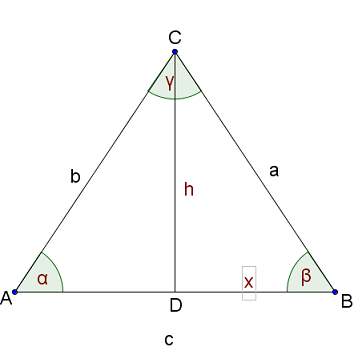
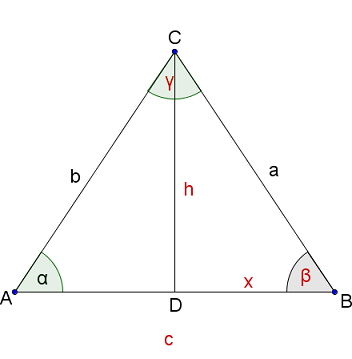
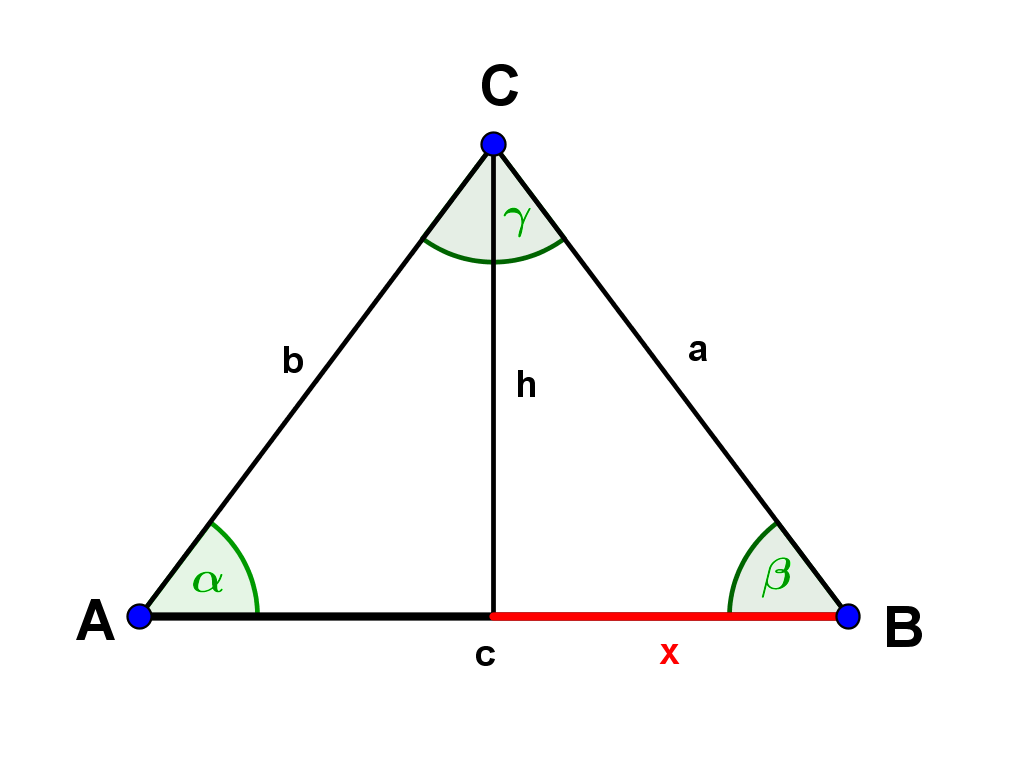
Berechne die fehlenden Seiten und Winkel des gleichschenkligen Dreiecks ABC mit . Beachte, dass wir allgemeine gleichschenklige Dreiecke betrachten, die nicht unbedingt rechtwinklig sind..
a=44,2cm
c=63,4cm
a=114,5m
=32,3°
c=35,4cm
=43,9°
h=14,8cm
28,3°
a=146,4m
h=58,4m
- 4
Bei tief stehender Abendsonne wirft Luise, welche groß ist, auf ebener Straße einen langen Schatten. Zeichne eine Skizze und berechne den Winkel, mit dem der Sonnenstrahl auf den Boden trifft.
Runde dein Ergebnis auf eine Nachkommastelle.
° - 5
Eine Tanne wirft einen langen Schatten. Die Sonnenstrahlen treffen dabei unter einem Winkel von auf die Erde. Zeichne eine Skizze und berechne die Höhe der Tanne.
Runde dein Ergebnis auf ganze Zahlen.
m - 6
Die Zugbrücke einer Burg ist 8m lang und hat zwischen der Mauer und der Kette einen Winkel von . Wie lang muss die Kette sein, mit der man die Zugbrücke hinunter klappen kann?
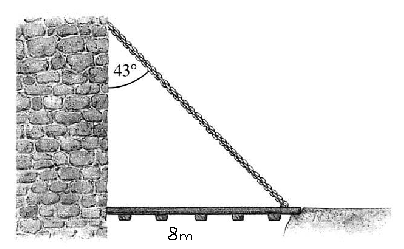 m
m - 7
Um die Breite eines Flusses zu bestimmen, hat man am einen Ufer die Strecke abgesteckt. Am anderen Ufer gibt es gegenüber von B einen Punkt C. Als Winkel zwichen AB und AC wird gemessen. Fertige zunächst eine Skizze an und berechne dann die Breite des Flusses.
m - 8
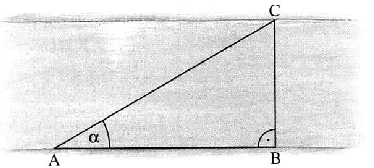
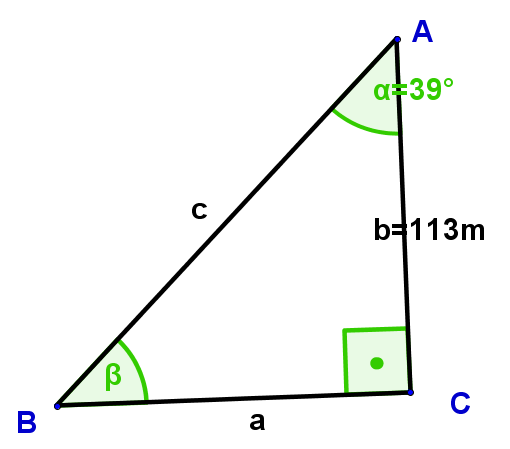
Ein Dreieck mit rechtem Winkel bei C, mit der Seite hat den Winkel . Fertige zunächst eine Skizze an und berechne dann alle fehlenden Seiten sowie den Winkel .
- 9
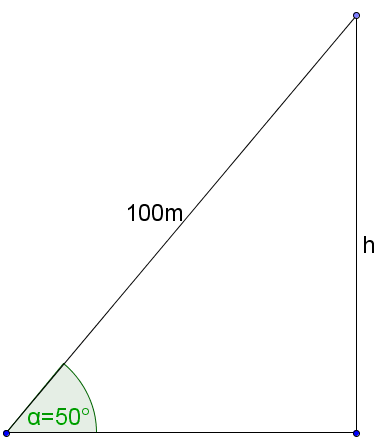
Ein Drachenflieger wird von einem Motorboot gezogen. Till schätzt vom Boot aus den Anstiegswinkel der 100 m langen, straff gespannten Schleppleine auf etwa 50°.
Wie hoch ist der Flieger etwa über dem Wasser?
m - 10
Beim "Fliegen" hinter dem Motorboot an einer 100m langen Leine soll aus Sicherheitsgründen die Flughöhe von 20m nicht überschritten werden.
Wie groß darf der Anstiegswinkel der Leine sein?
° - 11
Um eine Geschosshöhe von 3,20m durch eine Treppe zu überbrücken, stehen für die Ausladung 4,50m zur Verfügung.
Unter welchem Steigungswinkel ist die Treppenwange zuzuschneiden?
° - 12
Skizziere ein Rechteck mit den Seiten a=7cm und b=18cm und berechne die Winkel
zwischen einer Diagonalen und den Seiten
zwischen beiden Diagonalen
- 13
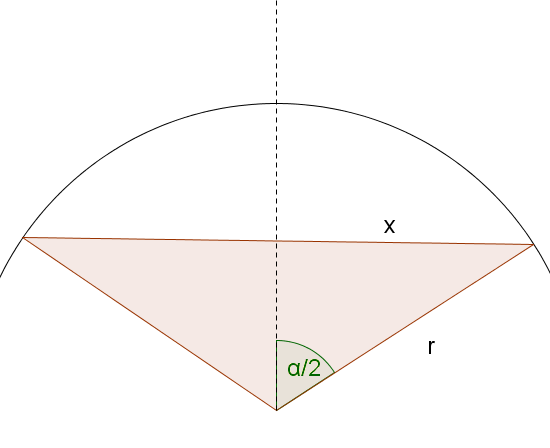
Im Kreis mit dem Radius gehört zur Sehne der Mittelpunktswinkel
Wie lang ist die Sehne?
cm - 14
In 50 m Länge soll ein Damm mit trapezförmigem Querschnitt aufgeschüttet werden. Unten soll er 18 m breit sein, oben 8 m. Der Böschungswinkel soll 50° betragen.
Berechne die Dammhöhe.
m - 15
Diese nicht maßstabsgetreue Skizze zeigt einen Würfel mit einer Seitenlänge von . Die Punkte und von sind die Mittelpunkte der Kanten des Würfels.
Berechne den Winkel .
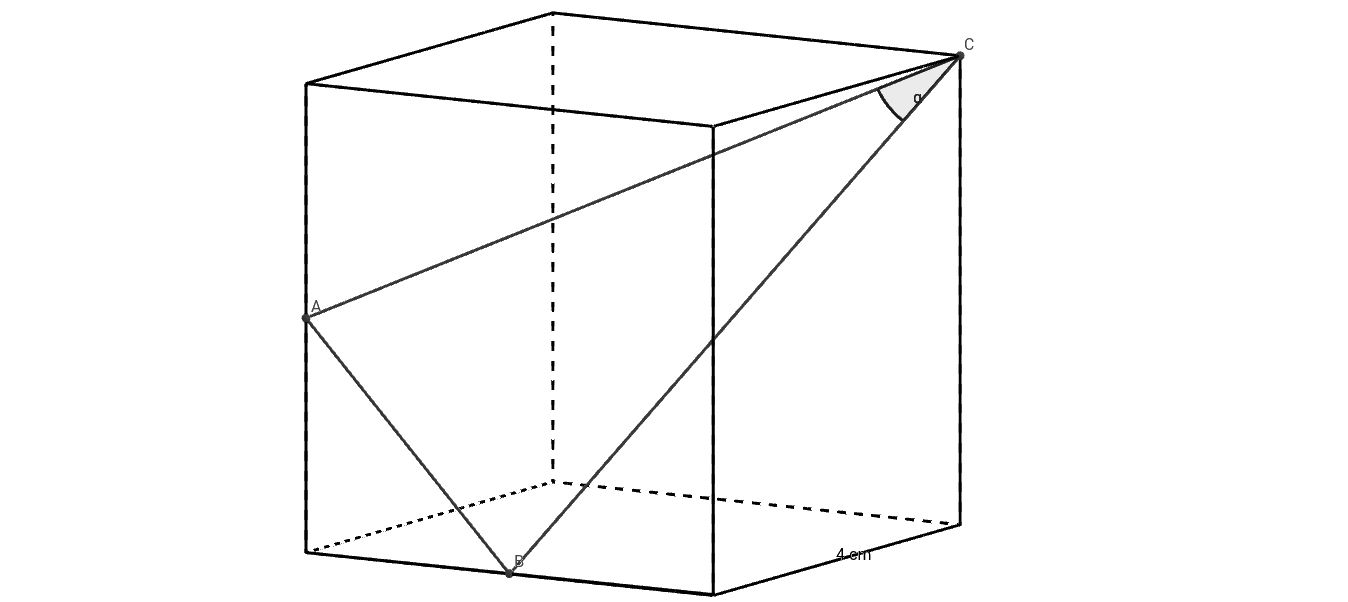
- 16
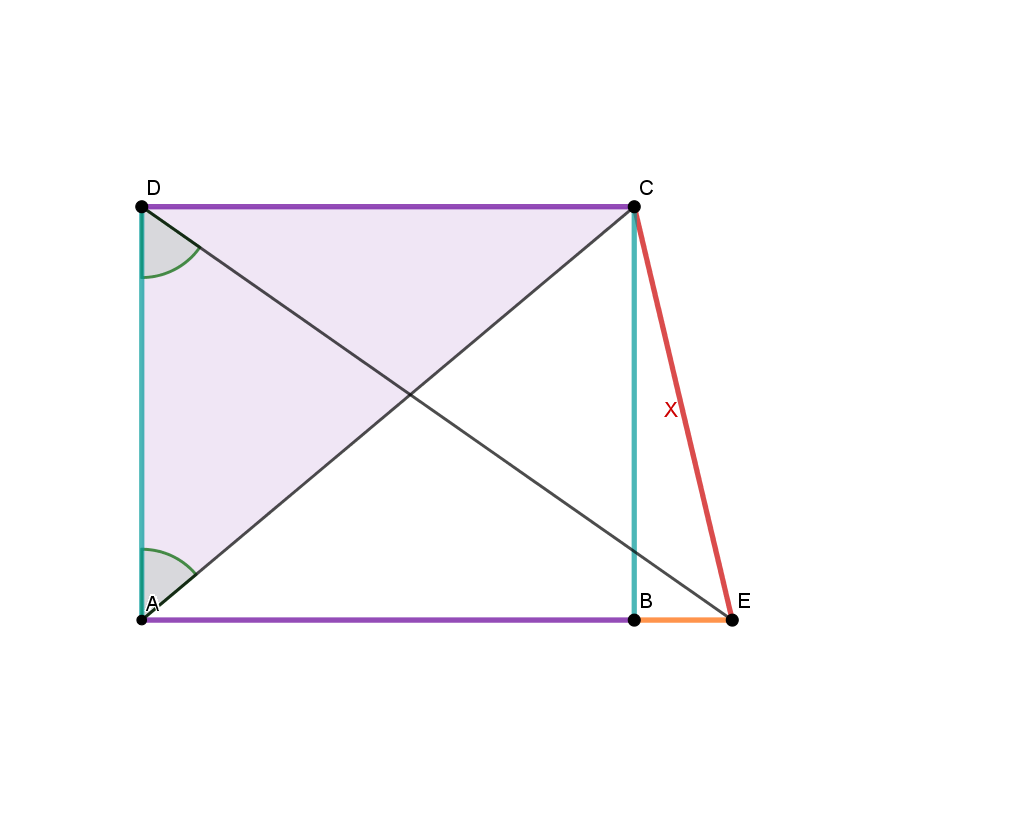
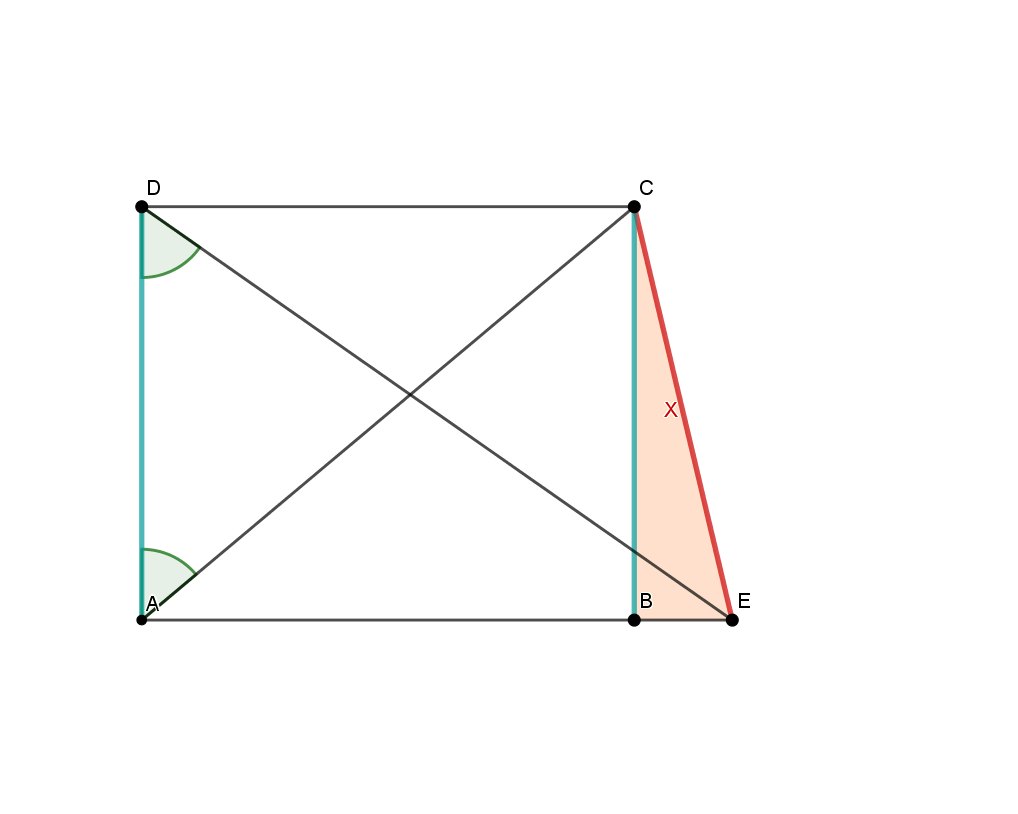
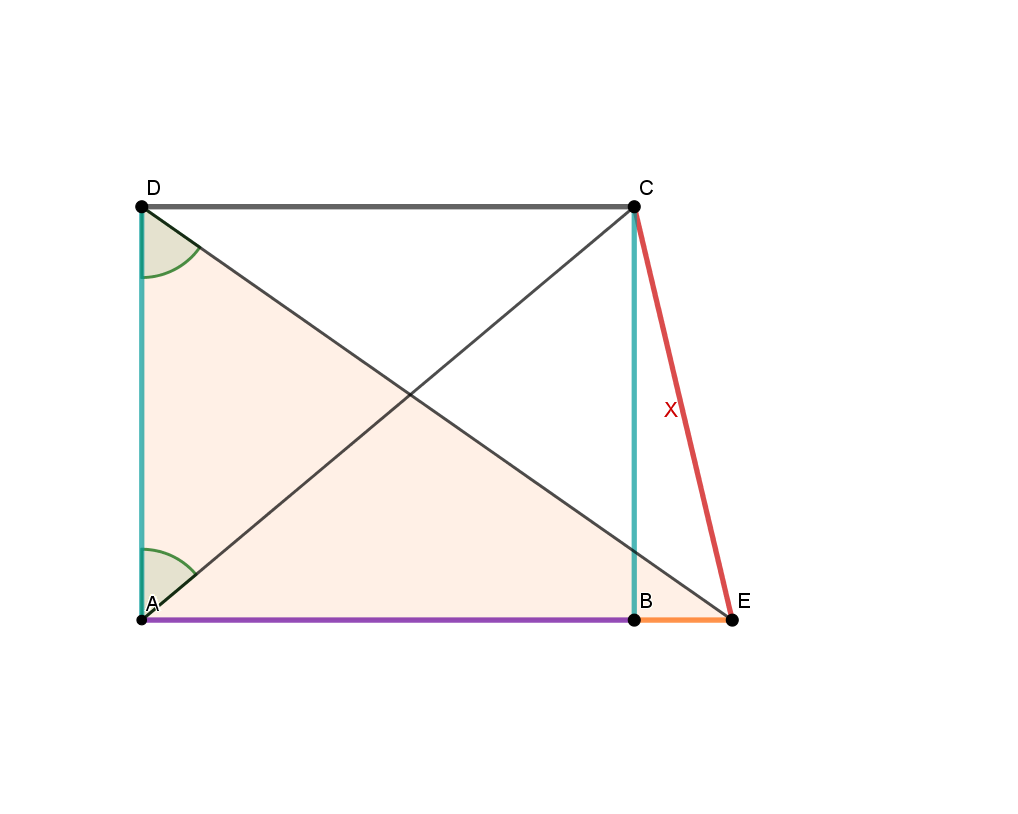
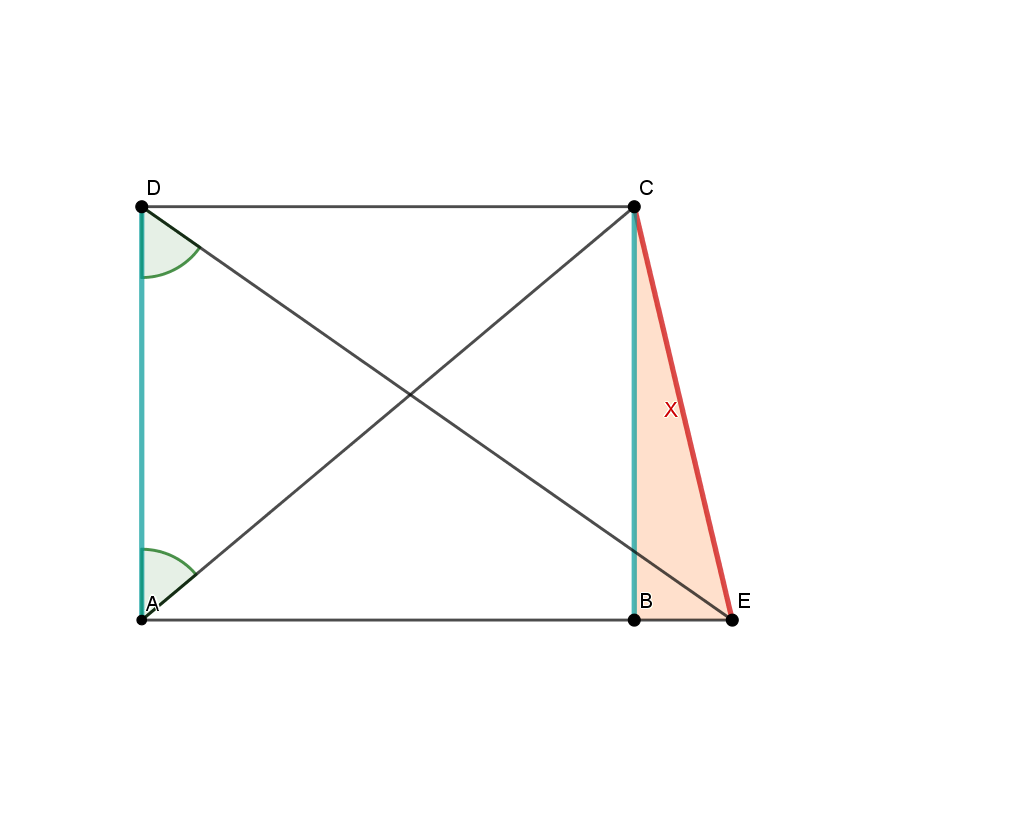
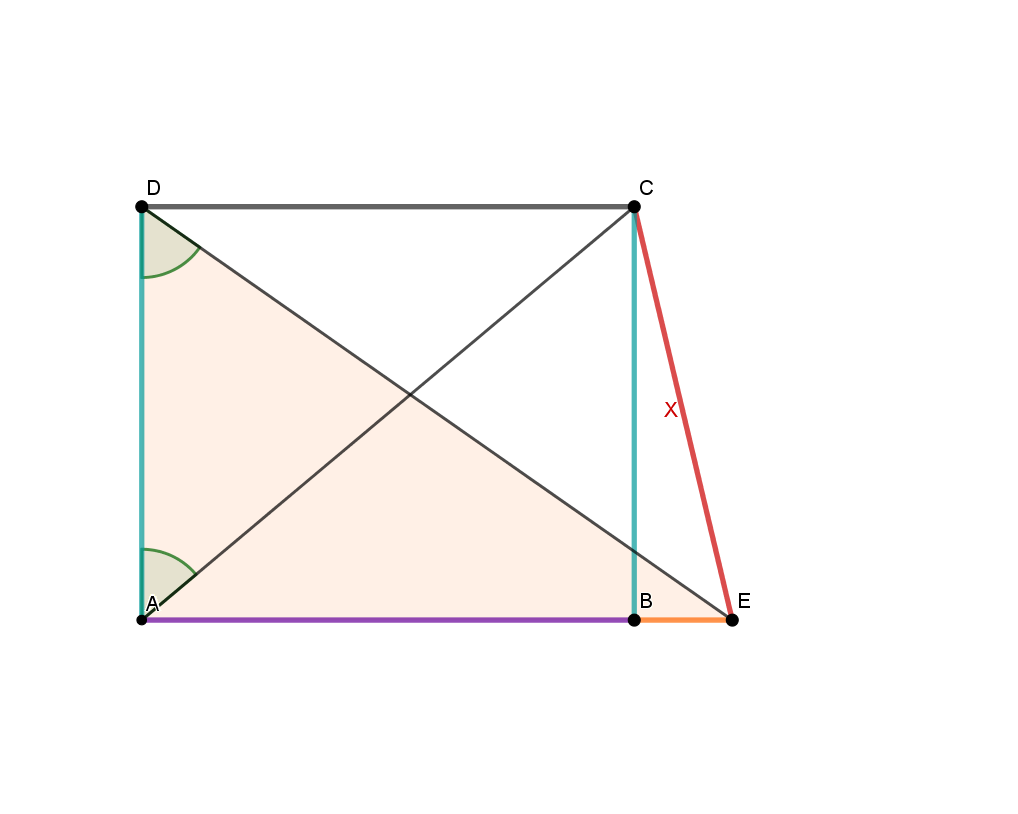
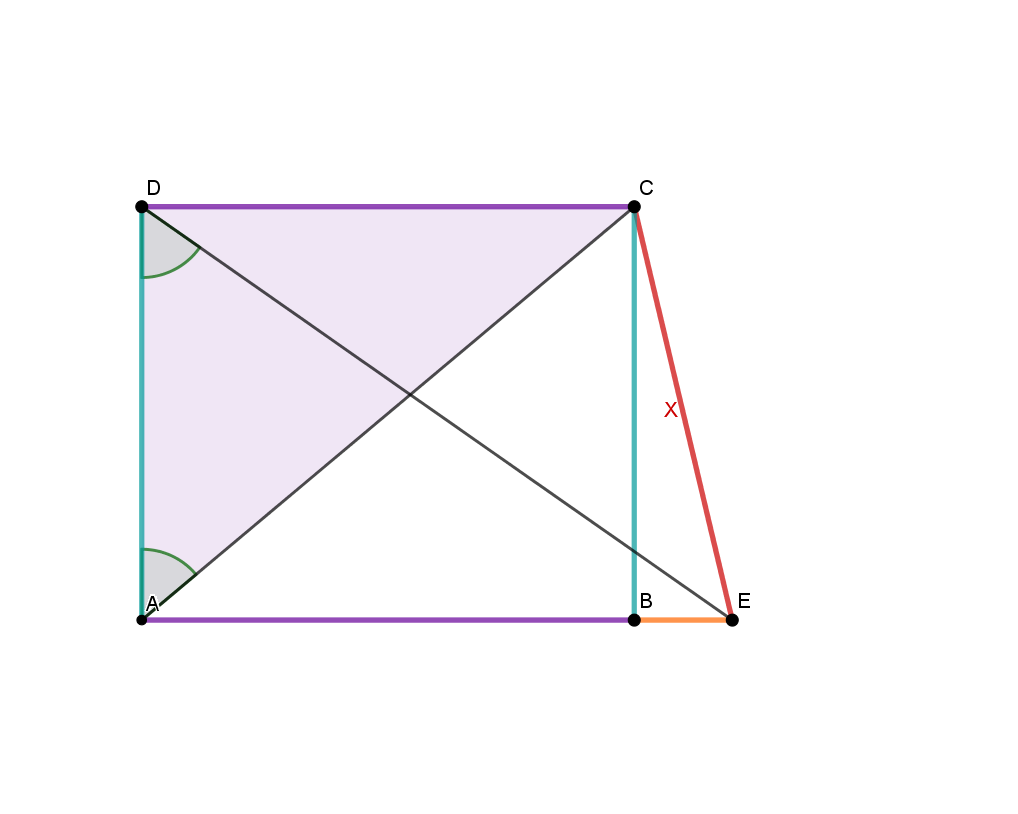
Diese nicht maßstabsgetreue Skizze zeigt ein Trapez mit den Längen:
Berechne die rot markierte Strecke
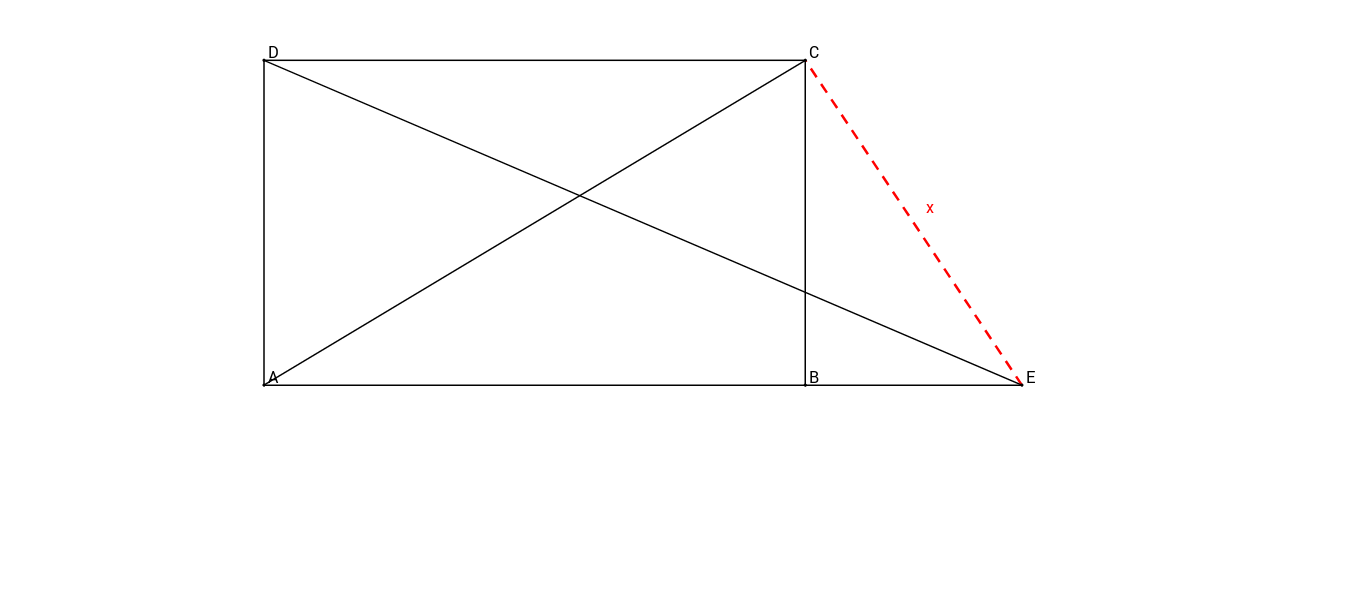 m
m - 17
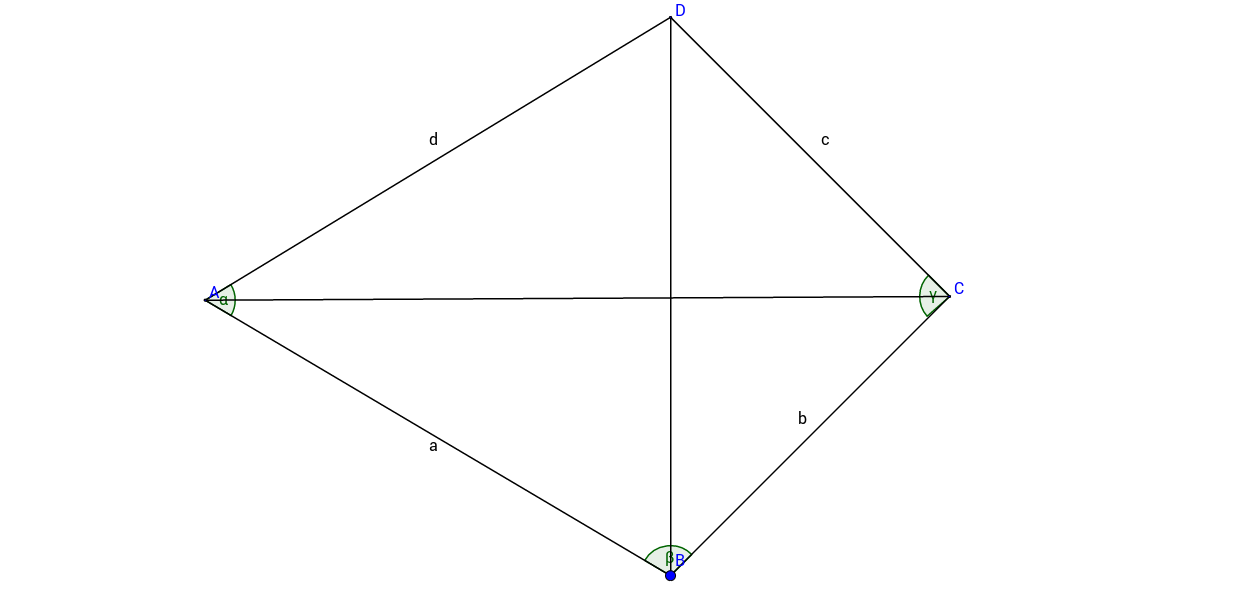
Diese nicht maßstabsgetreue Skizze zeigt ein Drachenviereck mit Symmetrieachse und den Maßen: , ,
Berechne die Winkel und .
- 18
Winkel gesucht
Diese nicht maßstabsgetreue Skizze zeigt ein Rechteck mit den Seitenlängen und .
Berechne den Winkel in ganzen Grad.
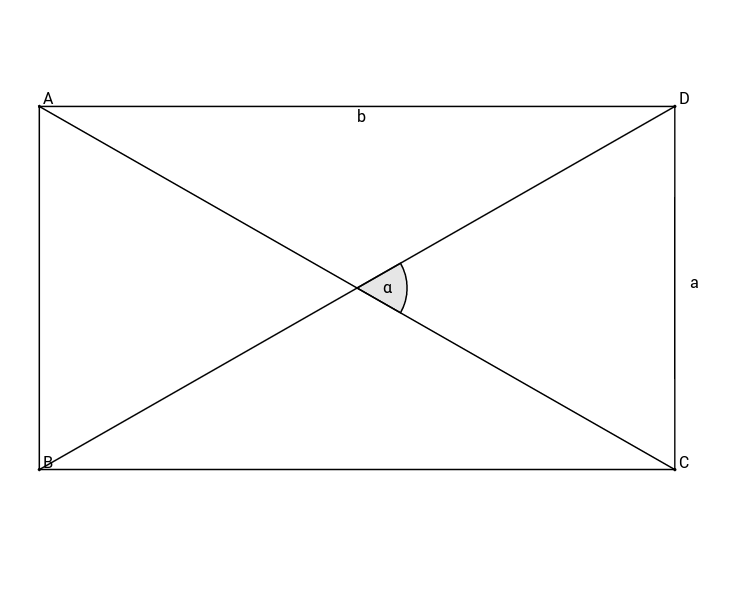
Skizze der Aufgabe
° - 19
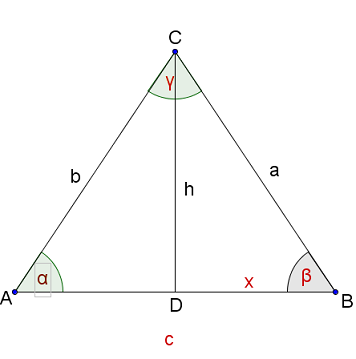
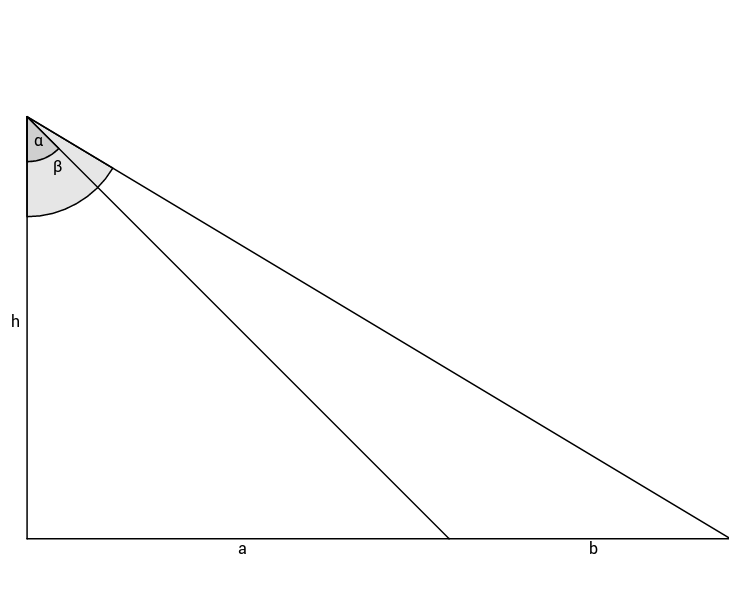
Diese Skizze zeigt ein nicht maßgetreues, rechtwinkliges Dreieck mit der Höhe und den Winkeln und .
Berechne die Seitenlängen und .
- 20
Der Steigungswinkel von Treppen soll laut DIN-Norm für Haupttreppen , für Nebentreppen betragen.
Die Geschosshöhe beträgt .
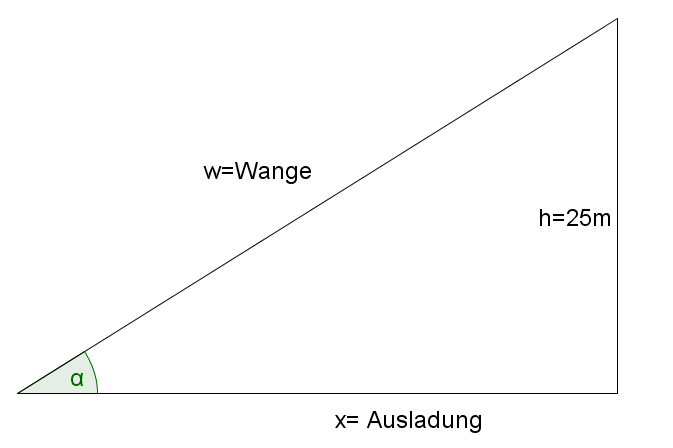
Wie lang wird die Treppenwange für . Berechne auch die Ausladung.
Wie lang wird die Treppenwange für . Berechne auch die Ausladung.
Wie lang wird die Treppenwange für . Berechne auch die Ausladung.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?