Gemischte Aufgaben zum Ableiten von Funktionen
Hier findest du gemischte Aufgaben rund um das Thema Ableiten von Funktionen. Übe, verschiedene Funktionstypen abzuleiten, mit Tangenten zu rechnen oder Sachaufgaben zu lösen.
- 1
Bilde die erste Ableitung folgender Funktionen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableiten von Polynomfunktionen
Die erste Ableitung wird wie folgt gebildet.
Für ist
Nicht vergessen, dass bei einem alleine stehenden "x" immer die Hochzahl "1" steht. Außerdem verwenden wir die Summenregel und dass die Ableitung von Konstanten Null ist:
Konstanten verschwinden beim Ableiten.
Potenzgesetz: jede Zahl hoch "0" ergibt "1", also ist
Somit ergibt die Ableitung dieser Funktion
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableiten von Polynomfunktionen
Bilde die erste Ableitung
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomfunktionen
Bilde die erste Ableitung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomfunktionen
Berechne die erste Ableitung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomfunktionen
Berechne die erste Ableitung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableiten von Potenzfunktionen
Schreibe die Wurzel als Potenz.
Bilde nun die erste Ableitung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Wende die Kettenregel an. Vergiss nicht die innere Funktion nach zu differenzieren.
Hast du eine Frage oder Feedback?
- 2
Achtung Blender unterwegs!
Zwei PKWs B und C fahren einander nachts mit Fernlicht auf einer Landstraße entgegen, deren Verlauf durch die Funktion
gegeben ist.
Von wo aus blenden die Scheinwerfer der Fahrzeuge einen Beobachter, der sich am Punkt A(-2|2) befindet?

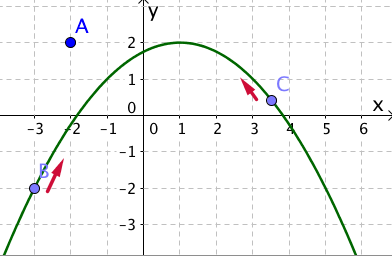
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentensteigung
Die Lösungsidee:
Ein Fahrzeug blendet den Beobachter, wenn seine Scheinwerfer "direkt" auf ihn gerichtet sind. Das ist der Fall, wenn es sich an einem Parabelpunkt befindet, dessen Tangente durch den Punkt A(-2|2) verläuft.
Erstelle die Tangente t im Punkt an p.
Berechne p'(x).
Setze in t ein.
Setze den Funktionswert ein.
Fasse zusammen und unterscheide dabei die Variable x und den festen Wert
Setze die Koordinaten (-2|2) von A ein, damit t durch A verläuft.
Bringe die quadratische Gleichung für in die übliche Normalform.
Multipliziere auf beiden Seiten mit 4.
Löse die Gleichung z.B. mit der Mitternachtsformel.
Setze beide Werte jeweils in ein.
Ergebnis: Der linke PKW blendet den Beobachter vom Punkt (-5|-7) aus, der rechte PKW vom Punkt (1|2) aus.
Bestätige das Rechenergebnis graphisch am folgenden Geogebra-Applet, indem du die Gleiterpunkte B und C verschiebst!
- 3
Bilde die Ableitung folgender Funktionen mit Brüchen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Hier wurde das Potenzgesetz angewendet, um die Funktion umzuformen. Leite nun ab:
Hast du eine Frage oder Feedback?
- 4
Bilde die Ableitung folgender e-Funktionen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung der e-Funktion
Bilde die erste Ableitung. Vergiss nicht, dass Minus im Exponenten nachzudifferenzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Bilde die erste Ableitung. Vergiss nicht, die im Exponenten nachzudifferenzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Bilde die erste Ableitung. Die vor der e-Funktion kommt vom Nachdifferenzieren des Exponenten .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Schreibe etwas oder füge mit ⊕ Elemente hinzu.
Bilde die erste Ableitung. Die vor der e-Funktion kommt vom Nachdifferenzieren des Exponenten .
Wenn du möchtest, kann du noch ein wenig vereinfachen:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Bilde nun die Ableitung. Vergiss nicht, die im Exponenten nachzudifferenzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Die äußere Funktion ist .
Die innere Funktion ist .
Die Ableitung der inneren Funktion ist .
Nun kannst du die Funktion direkt mit der Kettenregel ableiten.
Hast du eine Frage oder Feedback?
Überlege dir, was die äußere und innere Funktion ist. Leite die Funktion dann mit der Kettenregel ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Bilde die erste Ableitung. Die vor der e-Funktion kommt vom Nachdifferenzieren des Exponenten .
=
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Bevor du ableitest, bietet es sich an, den Bruch "aufzulösen". Das kannst du mit einem Minus vor dem Exponenten machen.
Bilde die erste Ableitung. Die vor der -Funktion kommt vom Nachdifferenzieren des Exponenten .
Wenn du möchtest, kannst du das Ergebnis noch einmal umformen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Produktregel
Die Funktion ist insgesamt ein Produkt mit den Faktoren und . Berechne zuerst die Ableitungen der Faktoren und .
Löse die Klammer auf.
Nun kannst du noch vereinfachen. Multiplizere dazu im zweiten Teil mit .
Wenn du noch weiter vereinfachen möchtest, kannst du z.B. ausklammern.
Hast du eine Frage oder Feedback?
Diese Aufgabe ist eine Kombination von Produkt und Kettenregel. Überlege dir, ob du zuerst Produkt oder Kettenregel anwenden musst.
- 5
Leite folgende Funktionen mit Logarithmus ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Leite ab, indem du die Produktregel nutzt. Es müssen die Ableitung von und gebildet werden.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zerlege zunächst in und .
und .
Dann ist .
Berechne die Ableitung von und .
Es gilt: und
Jetzt kannst du mit Hilfe der Kettenregel ableiten:
Diese ist für alle definiert.
Hast du eine Frage oder Feedback?
Um ableiten zu können musst du wissen, wann eine Funktion differenzierbar ist, was die Kettenregel ist und wie du die natürliche logarithmus Funktion ableiten kannst.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Kettenregel anwenden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Die Wurzel lässt sich als Potenz schreiben. Dann wendet man die Potenzregel des Logarithmus an.
In dieser Form kannst du die Ableitung der Funktion mit der Faktorregel berechnen:
Das fasst du noch zusammen und erhältst als Ergebnis:
Anmerkung: Die Faktorregel ist ein Spezialfall der Produktregel. Du kannst die Ableitung daher natürlich auch mit der Produktregel berechnen
Hast du eine Frage oder Feedback?
für .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Um ableiten zu können musst du wissen, wann eine Funktion differenzierbar ist, was die Kettenregel ist, wie du Wurzeln als Potenz schreiben und wie du die natürliche Logarithmusfunktion ableiten kannst.
Zerlege zunächst in und :
Dann ist .
Berechne die Ableitung von und :
Jetzt kannst du mit Hilfe der Kettenregel ableiten:
.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Mit Hilfe der Kettenregel ableiten.
Erst die äußere Ableitung (die äußere Funktion ableiten) bilden und die innere Funktion einsetzen. Dann noch Nachdifferenzieren, also mal die innere Ableitung (innere Funktion ableiten) nehmen.
↓ Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Als erstes wird mit Hilfe der Kettenregel abgeleitet.
Dann differenzierst du unter Verwendung der Quotientenregel nach.
Den Doppelbruch zu Beginn löst du auf, indem du den Kehrbruch des Nenners bildest.
↓ Nun kürzt du und musmultiplizierst aus im Zähler.
↓ Nun fasst du im Zähler zusammenfassen. Im Nenner wendest du die binomische Formel an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Wende die Ableitungsregel für den ln an. Das Argument des ln ist dann der Nenner eines Bruches mit dem Zähler 1. Differenziere dann mit der Ableitung des Arguments des nach.
↓ Kürze Zähler und Nenner des Bruches mit .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zum Ableiten des zweiten Elements zwei mal die Kettenregel anwenden.
↓ Mit 2 kürzen.
Hast du eine Frage oder Feedback?
für
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Wende die Ableitungsregel für den ln mit beliebigem Argument an und differenziere mit der Ableitung des Arguments nach (hier: lnx).
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Wende die Produktregel zum Ableiten an. Für den zweiten Faktor wird die Ableitungsregel des ln benötigt.
↓ Multipliziere die Klammer aus und kürze ein im zweiten Summanden.
Hast du eine Frage oder Feedback?
für
Erster Schritt, den Logarithmus in einfache Teile zerlegen
Zweiter Schritt, die Ableitung bilden
Wende die Kettenregel an.
↓ Kürze den 2.Term.
↓ Bringe den ersten Term auf den Hauptnenner.
↓ Fasse zusammen.
Hast du eine Frage oder Feedback?
- 6
Ableitungen von ln-Funktionen Teil 2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Mit Hilfe der Quotientenregel den Logarithmus umformen.
Den ersten Term vereinfachen.
Ableiten, beim ln mit der Kettenregel .
Den ersten Term zu einem Bruch mit dem gleichen Nenner umformen.
Die Brüche addieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Mit Hilfe der Kettenregel ableiten.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Mit Hilfe der Kettenregel ableiten .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Leite beide Elemente mit Hilfe der Kettenregel ab.
Nun wende die Logarithmusformel an:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Die ln-Funktion ist die Umkehrfunktion der e-Funktion, wodurch diese sich gegenseitig aufheben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zunächst stellen wir den Definitionsbereich fest: da keine ganze Zahl ist, ist der Ausdruck nur für positive definiert und positiv. Da wir dann den Logarithmus anwenden können, besteht der Definitionsbereich aus dem Intervall .
Wende die Potenzregel des Logarithmus an.
Wende die Ableitungsregel für den an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Leite mit Hilfe der Kettenregel ab.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Berechne die Ableitung von u () und v ().
f(x) mit Hilfe der Produktregel ableiten.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Ableitung berechnen
Wende zum Ableiten des ersten Summanden die Produktregel an.
Kürze den zweiten Summanden mit x.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zum Ableiten betrachte jeden Summanden einzeln. Für die Ableitung des ersten Summanden wende die Kettenregel sowie die Ableitungsregel für den an. Für den zweiten Summanden verwende nur die Ableitungsregel für den .
Multipliziere aus und vereinfache.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Wende die Kettenregel zum Ableiten an und differenziere mit der Ableitung von ln(x) nach.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Wende die Produktregel zum Ableiten an. Hierbei muss die Ableitung von und gebildet werden.
Um abzuleiten, wird jeder Summand gesondert betrachtet. Für die Ableitung der ersten beiden Summanden ist die Kettenregel notwendig, wobei mit der Ableitung von nachdifferenziert werden muss. Für den dritten Summanden muss die Ableitung von berechnet werden.
Multipliziere nun die Klammern aus.
Fasse jetzt zusammen.
Hast du eine Frage oder Feedback?
- 7
Bestimme alle Punkte, in denen die Funktion eine waagerechte Tangente besitzt
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung einer Potenzfunktion
Um diese Aufgabe zu lösen, solltest du wissen, wie man die Ableitung einer Potenzfunktion bestimmt.
Die Punkte mit waagrechter Tangente am Funktionsgraph von sind genau die, in denen die Steigung der Funktion ist:
↓ Bilde die Ableitung, indem du die Summenregel verwendest.
↓ Der Wert der Ableitung an einer Stelle entspricht der Steigung an dieser Stelle. Setze die Ableitung gleich 0.
↓ Löse nach x auf.
Für erhalten wir den einzigen Punkt, der eine waagerechte Tangente besitzt.
Bestimme den zugehörigen y-Wert, indem du berechnest.
↓ Werte den Term aus.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung einer Potenzfunktion
Um diese Aufgabe zu lösen, solltest du wissen, wie man die Ableitung einer Potenzfunktion bestimmt.
Die Punkte mit waagrechter Tangente am Funktionsgraph von sind genau die, in denen die Steigung der Funktion ist:
↓ Bilde die Ableitung, indem du die Summenregel verwendest.
↓ Der Wert der Ableitung an einer Stelle entspricht der Steigung an dieser Stelle. Setze die Ableitung gleich 0.
↓ ↓ Lies die Lösungen ab. Beachte dabei, dass ein Produkt immer dann ist, wenn einer seiner Faktoren ist.
und
Berechne die zugehörigen Funktionswerte.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Um diese Aufgabe zu lösen, solltest du wissen, wie man die Produktregel anwendet und die Ableitung der Exponentialfunktion bestimmt.
Die Punkte mit waagrechter Tangente am Funktionsgraph von sind genau die, in denen die Steigung der Funktion ist:
↓ Bilde die Ableitung durch Verwendung der Produktregel. Beachte auch, dass du bei die Kettenregel verwendest.
↓ ↓ Der Wert der Ableitung an einer Stelle entspricht der Steigung an dieser Stelle. Setze die Ableitung gleich .
↓ Ein Produkt ist genau dann , wenn einer seiner Faktoren ist. Die Exponentialfunktion ist jedoch immer größer für alle . Deswegen musst du nur gleich Null setzen.
↓ Löse nach x auf. Ziehe zuerst auf beiden Seiten ab.
↓ Teile durch 2
↓ Berechne den zugehörigen Funktionswert.
↓ Berechne den Exponenten und wende das Potenzgesetz an.
Hast du eine Frage oder Feedback?
- 8
Ordne die Ableitungen richtig zu!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Lösung

Erläuterung:
Die Funktionen und die verwendeten Ableitungsregeln:
Funktion 1: Potenzfunktion
Funktion 2: Produktregel
Funktion 3: Exponentialfunktion und Kettenregel
Funktion 4: Quotientenregel
Funktion 5: Trigonometrische Funktion und Kettenregel
Funktion 6: Wurzelfunktion
Funktion 7: ln-Funktion
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
