1 Übersicht
Kursinhalt
In diesem Kurs lernst du, wie du Wurzelfunktionen mithilfe der Potenzgesetze so umformen kannst, dass die Ableitung und Stammfunktion einfach gebildet werden kann.
Voraussetzungen
Du solltest bereits folgende Themen kennen:
Ableiten mithilfe der Potenzregel, Produktregel, Faktorregel und Kettenregel
Kursdauer
ungefähr 60-90 Minuten.
2 Wurzelfunktionen
Eine Wurzelfunktion ist eine Funktion, in der eine Variable unter einer Wurzel steht. Dabei kann es sich um eine Quadratwurzel oder eine Wurzel höherer Ordnung handeln.
Beispiele für Wurzelfunktionen:
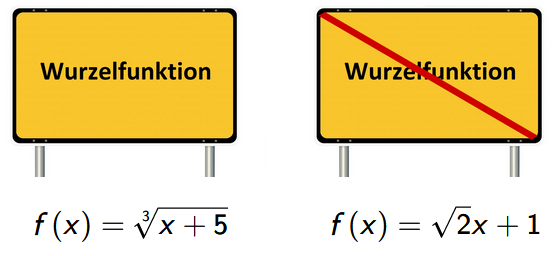
Ableitung von Wurzelfunktionen
Wurzelfunktionen kannst du ableiten, indem du diese erst in eine Potenzfunktion mit rationalem Exponenten umformst und dann mithilfe der Ableitungsregeln ableitest. Diese Vorgehensweise wird auf den nächsten Seiten vertieft und ausführlich gezeigt.
3 Von der Wurzel zur Potenz
Wurzeln können auch durch Potenzen dargestellt werden.
Dabei wird die Wurzelfunktion zu einer Potenzfunktion mit rationalem Exponenten. Der Radikand wird zur Basis der Potenz und der Wurzelexponent zum Nenner im Bruch vom Exponenten.
Wurzelexponent Nenner im Bruch vom Exponenten
Beispiele:
4 Allgemeine Wurzel umformen
Wenn der gesamte Radikand eine Potenz ist, dann kann er anhand der Potenzgesetze für rationale Exponenten umgeformt werden, um die Wurzel aufzulösen.
| ↓ | Forme die Exponenten anhand der Potenzgesetze um. | ||
| ↓ | Vereinfache den Exponenten. | ||
Summe, Differenz, Produkt und Quotient als Radikand
Wie du in den Beispielen siehst, wird stets der ganze Radikand zur Basis der Potenzfunktion.
Bei Summen und Differenzen wird der gesamte Radikand gemeinsam zur Basis:
Bei Produkten und Quotienten darfst du die Bestandteile auch aufspalten und musst dann aber für jeden Faktor den Exponenten anpassen:
5 Ableitung mithilfe der Potenzregel
Auf der vorherigen Kursseite wurde die Wurzelfunktion in eine rationale Potenzfunktion umgeformt. Diese kannst du nun mithilfe der Ableitungsregel für Potenzfunktionen ableiten.
Beispiel 1:
| ↓ | Leite mit der Ableitungsregel für Potenzfunktionen ab. | ||
| ↓ | Vereinfache den Exponenten. | ||
| ↓ | Da der Exponent negativ ist, kannst du den Term mit dem Potenzgesetz für negative Exponenten in einen Bruch umformen. | ||
| ↓ | Der Bruch im Exponenten ergibt nach Anwendung des Potenzgesetzes für rationale Exponenten wieder eine Wurzel. | ||
Die Ableitung von ist .
Beispiel 2:
| ↓ | Leite mit der Ableitungsregel für Potenzfunktionen ab. | ||
| ↓ | Vereinfache den Exponenten. | ||
| ↓ | Da der Exponent negativ ist, kannst du den Term mit dem Potenzgesetz für negative Exponenten in einen Bruch umformen. | ||
| ↓ | Der Bruch im Exponenten ergibt nach Anwendung des Potenzgesetzes für rationale Exponenten wieder eine Wurzel. | ||
Die Ableitung von ist .
6 Übung zu einfachen Ableitungen
Laden
7 Exkurs: Ableitung der Wurzelfunktion über h-Methode
Die Funktion soll mithilfe der h-Methode abgeleitet werden. Ohne die Verwendung der Regel zur Ableitung von Potenzfunktionen wirst du den Differenzenquotienten aufstellen und daraus den Differentialquotienten bilden, den du mit der h-Methode zur Ableitung umformst.
| ↓ | Setze für die Wurzelfunktion ein. | ||
| ↓ | Erweitere den Bruch mit . | ||
| ↓ | Multipliziere den Zähler aus, indem du die 3. binomische Formel anwendest. | ||
| ↓ | Vereinfache die Quadrate im Zähler. | ||
| ↓ | Vereinfache den Zähler. | ||
| ↓ | Kürze den Faktor . | ||
| ↓ | Bestimme den Grenzwert. | ||
| ↓ | Fasse die Wurzeln im Nenner zusammen. | ||
Mit dieser Rechnung konntest du dich überzeugen, dass die Regel zum Ableiten von Potenzfunktionen auch bei Quadratwurzeln die gleiche Ableitung liefert.
Das bedeutet auch, dass Wurzelfunktionen einfacher abgeleitet werden können, wenn diese zunächst mit der Regel für allgemeine Brüche in Exponenten in eine Potenz umgeschrieben werden. Allgemein gilt:
Ableitung der Quadratwurzel
Ableitung der n-ten Wurzel
8 Summe und Differenz im Radikand: Umformen und dann...
Du bekommst die Aufgabe, folgende Funktion abzuleiten:
Wie du es gerade gelernt hast, bereitest du die Funktion zunächst für das Ableiten vor, indem du das Potenzgesetz für rationale Exponenten anwendest:
Und jetzt?!
Damit du diese Funktion ableiten kannst, benötigst du die Kettenregel!
Wie die Kettenregel dir beim Ableiten von Wurzelfunktionen hilft, lernst du auf der nächsten Folie.
9 ....Kettenregel!
Hat die Wurzelfunktion im Radikanden eine Summe oder Differenz, wirst du die Kettenregel brauchen, da du beim Umschreiben in eine Potenzfunktion mit rationalen Exponenten den Radikanden nicht aufspalten kannst.
Bei der Kettenregel gibt es eine innere Funktion und eine äußere Funktion . Hat man die Wurzelfunktion in eine Potenzfunktion mit rationalen Exponenten umgeschrieben, so ist die Basis der Funktion (zuvor der Radikand) jetzt die innere Funktion und der Exponent (zuvor Wurzel und Potenz des Radikanden) ist Exponent die äußere Funktion mit der Basis :
innere Funktion: , äußere Funktion:
Allgemeines Vorgehen
Hast du eine Wurzelfunktion, die du ableiten sollst, so kannst du mithilfe der Kettenregel und der Potenzgesetze immer so vorgehen:
Schreibe die Wurzelfunktion in eine Potenzfunktion mit rationalen Exponenten um.
Identifiziere die innere und die äußere Funktion und leite diese zur Vorbereitung ab.
Setze , und in die Kettenregel ein.
Vereinfache und forme gegebenenfalls erneut mit den Potenzgesetzen um.
Ein Beispiel findest du auf der nächsten Folie!
10 Die Kettenregel am Beispiel
Schau dir das Beispiel von vorher nochmal an:
Innere Funktion vorbereiten
Die innere Funktion ist die Basis der Potenzfunktion.
Leite die Funktion mithilfe der Ableitungsregel für Potenzfunktionen ab.
Äußere Funktion
Die äußere Funktion ist der Exponent der Potenzfunktion zur neuen Basis .
Leite die Funktion mithilfe der Ableitungsregel für Potenzfunktionen ab.
Subtrahiere im Exponenten.
Kettenregel anwenden
| ↓ | Setze die Ergebnisse von oben ein. Beachte, dass die Funktionen und verkettet werden. | ||
| ↓ | Berechne . | ||
| ↓ | Da der Exponent der Klammer negativ ist, kannst du den Term mit dem Potenzgesetz für negative Exponenten in einen Bruch umformen. | ||
| ↓ | Der Bruch im Exponenten von ergibt nach Anwendung des Potenzgesetzes für rationale Exponenten wieder eine Wurzel. | ||
| ↓ | |||
11 Übungen mit Potenzgesetzen und Kettenregel
Laden
12 Zusatzwissen: Stammfunktionen von Wurzelfunktionen
Die Tipps zur Umformung von Wurzelfunktionen sind auch für das Bilden der Stammfunktionen essentiell!
Damit du die Stammfunktion bilden kannst, solltest du zuerst zu einer Potenzfunktion mit rationalen Exponenten umformen und danach folgende Regel befolgen:
,
Beispiel
Bilde die Stammfunktion der folgenden Funktion :
| ↓ | Forme mit dem Potenzgesetz für rationalen Exponenten um. | ||
| ↓ | Verwende die oben beschriebene Regel zum Bilden der Stammfunktion. | ||
| ↓ | Addiere im Exponenten und im Nenner. | ||
| ↓ | Dividieren durch einen Bruch = Multiplizieren mit dem Kehrbruch. | ||
| ↓ | Verwende das Potenzgesetz für rationale Exponenten, um wieder zu einer Wurzel umzuformen. | ||
13 Zusammenfassung
In diesem Kurs hast du gelernt, wie du Wurzelfunktionen vorbereiten kannst, um sie einfacher integrieren und ableiten zu können.
Hier ist ein Überblick über die Dinge, die du brauchst:
Wurzelterme umformen
Bevor du ableiten kannst, musst du die Wurzelfunktion zu einer Potenzfunktion mit rationalen Exponenten umformen.
Besonderes:
wird zu ,
ist die Quadratwurzel und wird zu .
Ableiten mit der Kettenregel
Hat man die Funktion umgeformt, so ist die Basis die innere Funktion und der Exponent wird mit die äußere Funktion. Nachdem du und gebildet hast, kannst du diese in die Kettenregel einsetzen.
Stammfunktion bilden
Möchte man, nachdem man die Wurzelfunktion umgeformt hat, die Stammfunktion bilden, verwendet man folgende Regel:
Übrigens: Einen ähnlichen Kurs gibt es auch zum Ableiten von Bruchtermen.

