Von einem außerhalb einer Kugel liegenden Punkt können unendlich viele Tangenten an die Kugel gelegt werden. Diese Tangenten bilden einen (doppelten) Kreiskegel, den Tangentialkegel der Kugel mit der Spitze . Die Berührpunkte aller Tangenten mit der Kugel liegen auf einem Kreis, den die Ebene aus der Kugel ausschneidet. Diese Ebene wird auch Polarebene genannt.
Hinweis: In der Abbildung sind Tangenten eingezeichnet.
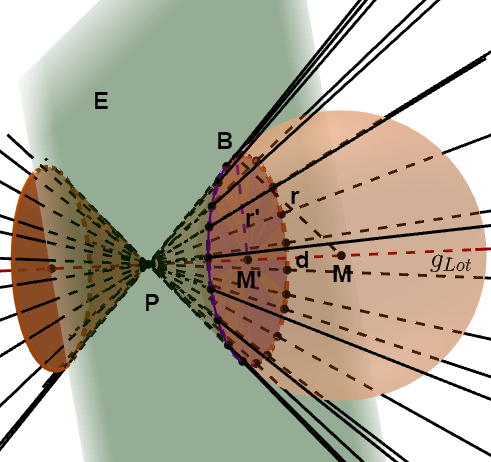
Alle Berührpunkte der Tangenten mit der Kugel liegen auf einem Kreis, den die Ebene
aus der Kugel ausschneidet.
Beispiel für die Erstellung der Ebenengleichung
Gegeben sind eine Kugel mit Kugelmittelpunkt , Kugelradius und ein Punkt außerhalb der Kugel. Vom Punkt aus werden Tangenten an die Kugel gelegt. Alle Berührpunkte der Tangenten mit der Kugel liegen auf einem Kreis, den die Ebene aus der Kugel ausschneidet. Bestimme die Gleichung der Ebene in Koordinatenform.
Benutze die Ebenengleichung und setze die gegebenen Werte ein.
| ↓ | Setze , und ein. | ||
| ↓ | Vereinfache. | ||
| ↓ | Berechne das Skalarprodukt. | ||
| ↓ | Vereinfache. | ||
Antwort: Die Gleichung der Ebene lautet .
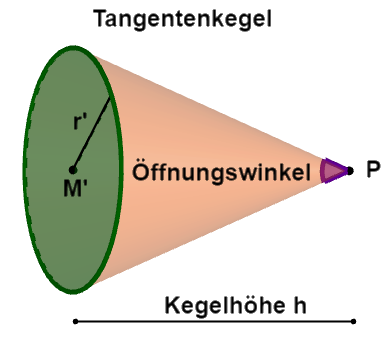
Der Tangentenkegel
Beim Tangentenkegel können
der Mittelpunkt des Schnittkreises
der Schnittkreisradius
der Öffnungswinkel
das Kegelvolumen
berechnet werden.
Berechnung des Schnittkreismittelpunktes
Den Mittelpunkt des Schnittkreises berechnest du, indem du die Lotgerade von auf die Ebene mit der Ebene schneidest:
Verwende als Aufpunkt den Mittelpunkt und als Richtungsvektor den Normalenvektor der Ebene :

Beispiel für die Berechnung des Schnittkreismittelpunktes
Gegeben sind die Schnittkreisebene und der Kugelmittelpunkt . Gesucht ist .
Berechne die Gleichung der Lotgeraden durch den Mittelpunkt auf die Ebene .
Verwende als Aufpunkt den Mittelpunkt und als Richtungsvektor den Normalenvektor der Ebene .
Schneide die Lotgerade mit der Ebene
| ↓ | Löse die Klammern auf. | ||
| ↓ | Vereinfache. | ||
| ↓ | Löse nach auf. | ||
Zur Berechnung des Schnittpunktes setzt du in die Gleichung der Lotgeraden ein.
Antwort: Der Mittelpunkt des Schnittkreises hat die Koordinaten
.
Berechnung des Schnittkreisradius
Mit dem Satz von Pythagoras berechnest du den Schnittkreisradius . Der Abstand der Ebene vom Mittelpunkt ist .
Dann gilt im rechtwinkligen Dreieck : . Für der Schnittkreisradius folgt daraus:
.

Beispiel für die Berechnung des Schnittkreisradius
Gegeben sind der Kugelmittelpunkt , der Mittelpunkt des Schnittkreises und der Kugelradius . Gesucht ist .
Berechne den Vektor und dann dessen Betrag .
| ↓ | Setze und ein. | ||
| ↓ | Vereinfache | ||
| ↓ | Berechne die Differenz. | ||
Antwort: Der Schnittkreisradius beträgt .
Berechnung des Öffnungswinkels des Tangentialkegels
Im rechtwinkligen Dreieck gilt:
bzw.

Beispiel für die Berechnung des Öffnungswinkels des Tangentialkegels
Gegeben sind der Kugelmittelpunkt , der Kugelradius und der Punkt . Gesucht ist der Öffnungswinkel .
Für den halben Öffnungswinkel gilt:
Berechne den Vektor und dann dessen Betrag.
Antwort: Der Öffnungswinkel des Tangentialkegels beträgt etwa .
Volumenberechnung des Tangentialkegels

Beispiel für die Berechnung des Tangentialkegelvolumens
Gegeben sind der Mittelpunkt des Schnittkreises , der Punkt und der Schnittkreisradius . Gesucht ist .
Der Kegelradius ist gleich dem Schnittkreisradius und die Kegelhöhe ist die Länge der Strecke .
Berechne den Vektor und dann dessen Betrag.
Berechne nun das Volumen des Kegels:
| ↓ | Setze und in die Volumenformel ein | ||
| ↓ | Vereinfache. | ||
Antwort: Das Volumen des Tangentialkegels beträgt etwa .
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Kugeln in der analytischen Geometrie
- Tangentialebene an eine Kugel
- Lagebeziehungen zwischen Kugeln und Punkten
- Lagebeziehung zwischen Kugeln und Geraden
- Lagebeziehung zwischen Kugeln und Ebenen
- Gegenseitige Lage von zwei Kugeln
- Zwei Kugeln mit gemeinsamen äußeren Berührpunkt
- Zwei Kugeln mit gemeinsamen inneren Berührpunkt
- Zwei sich schneidende Kugeln
