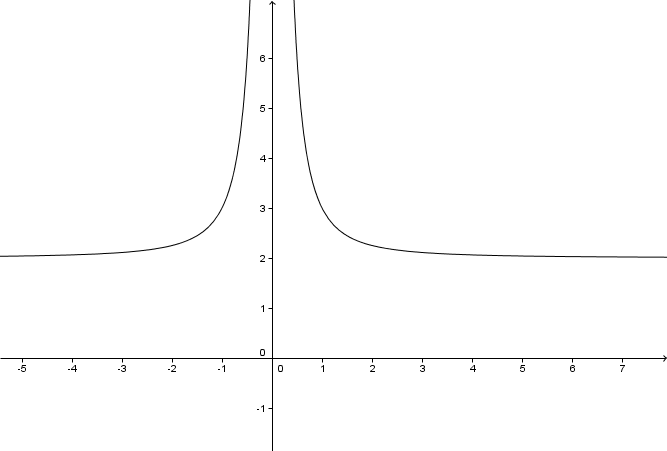
Aufgaben zu gebrochen-rationalen Funktionen
- 1
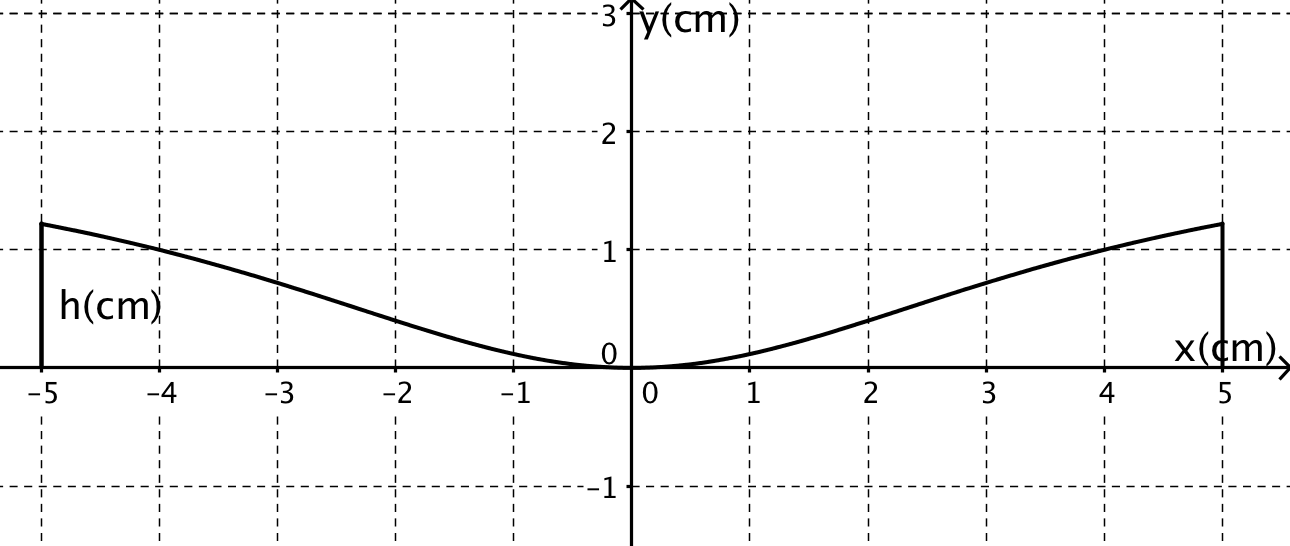
Der Querschnitt einer kreisrunden Wasserschale wird von drei Strecken und dem Graphen der Funktion berandet (siehe Zeichnung; Maßstab 1:10).
Berechne die Wassertiefe in der Schale, wenn die Wasserbreite 40 cm beträgt.
- 2
Bestimme den maximal möglichen Definitionsbereich folgender gebrochenrationaler Funktionen:
- 3
Wie ändert sich der Wert des Terms , wenn x „immer größer“ bzw. „immer kleiner“ wird?
- 4
Gegeben ist der Term .
Berechne T(4), T(–5) und .
Welchen Wert der Variablen a darfst du nicht in diesen Term einsetzen?
Erläutere, wo diejenigen Zahlen auf dem Zahlenstrahl liegen, die beim Einsetzen möglichst große Termwerte ergeben.
- 5
Gegeben ist der Bruchterm .
Gib die Definitionsmenge des Terms an.
Fasse die beiden Brüche zusammen und vereinfache.
Berechne T(3).
- 6
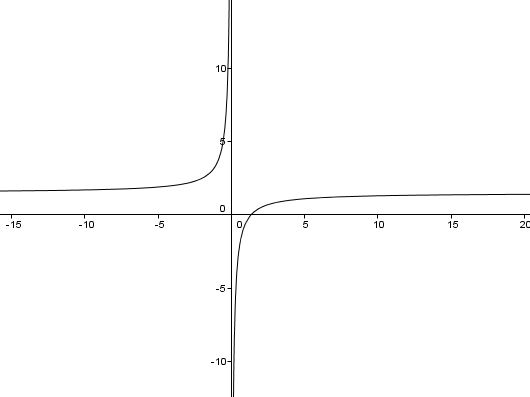
Gegeben ist die Funktion
Bestimme die Nullstelle der Funktion h.
An welcher Stelle nimmt die Funktion h den Wert 4 an ?
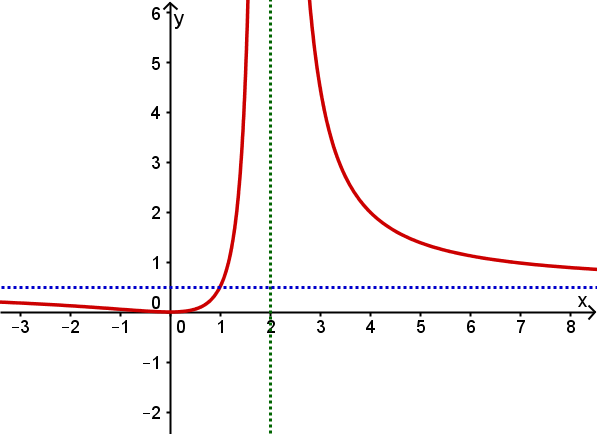
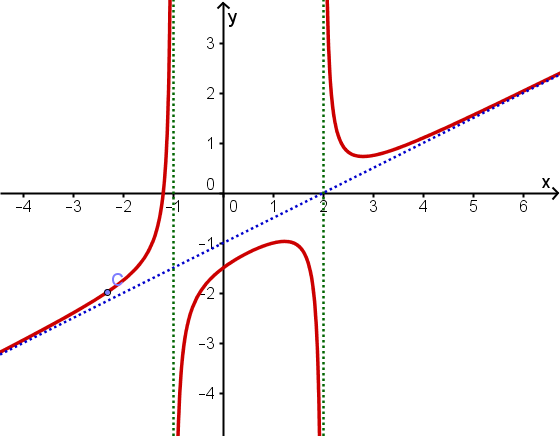
- 7
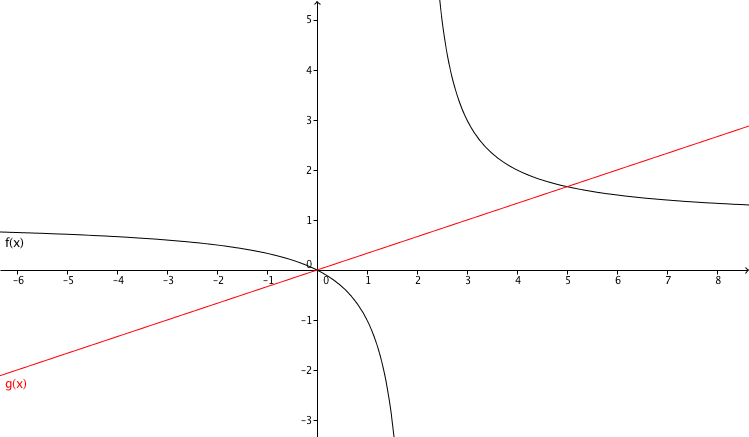
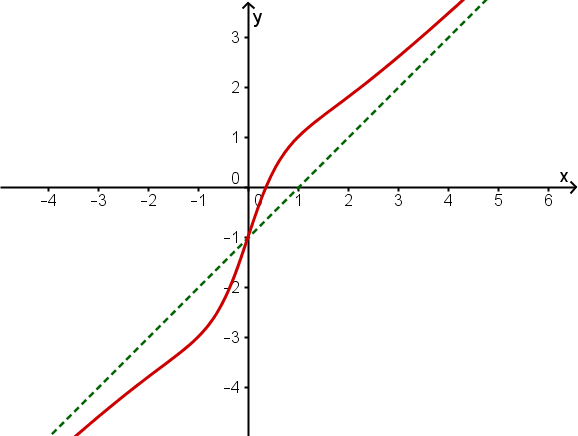
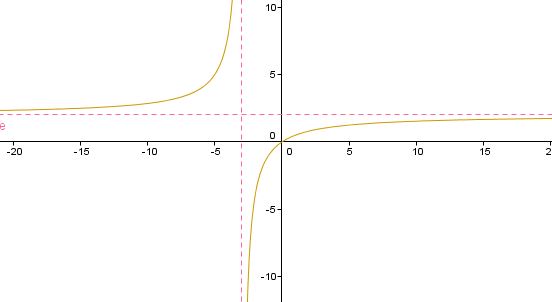
Gegeben ist der Graph einer linearen und einer gebrochenrationalen Funktion
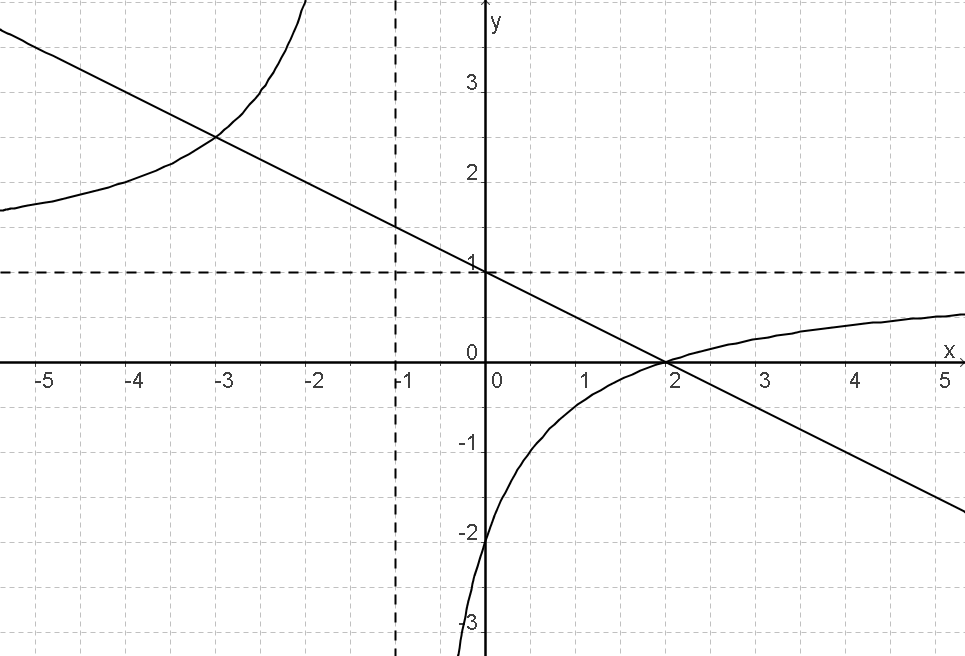
Die Zeichnung zeigt die Graphen der Funktionen mit den Funktionsgleichungen und .
Bestimme anhand der Zeichnung die Lösungsmenge der Gleichung .
Tipp: Gib deine Lösungen in aufsteigender Reihenfolge und durch ein Leerzeichen getrennt ein.
Bestimme mit Hilfe des gegebenen Funktionsgraphen die Lösungsmenge der Gleichung .
- 8
Zeichne die Graphen zu den Termen und in ein Koordinatensystem.
- 9
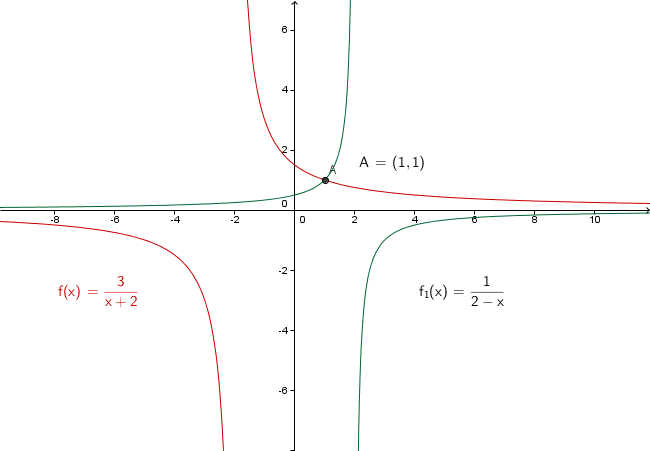
Zeichne die Graphen der Funktionen und
Lies die Koordinaten des Schnittpunkts der Graphen aus der Zeichnung ab und überprüfe dein Ergebnis rechnerisch. Trage dein Ergebnis gerne in das Eingabefeld unten in der Form ( | ), also z.B. (5|2), ein, bevor du dann in die Lösung schaust ;)
- 10
Gegeben ist die Funktion f mit der Abbildungsvorschrift .
Welche Zahl kann nicht in der Definitionsmenge enthalten sein?
Berechne f(10), f(100), f(1000).
Lege eine Wertetabelle an und zeichne den Funktionsgraphen.
Gib die Gleichungen der Asymptoten von an.
- 11
Gib den maximal möglichen Definitionsbereich an und untersuche das Verhalten des Graphen an den Definitionslücken sowie für . Skizziere den Graphen.
- 12
Zeichne mit Hilfe einer Wertetabelle die Graphen zu folgenden Funktionsgleichungen; bestimme waagrechte und senkrechte Asymptote.
- 13
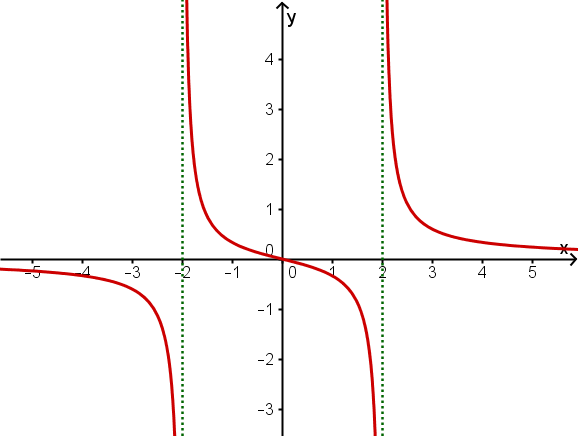
Spiegeln, verschieben, stauchen
Zeichne den Graphen der Funktion und bestimme damit die Graphen von , und
- 14
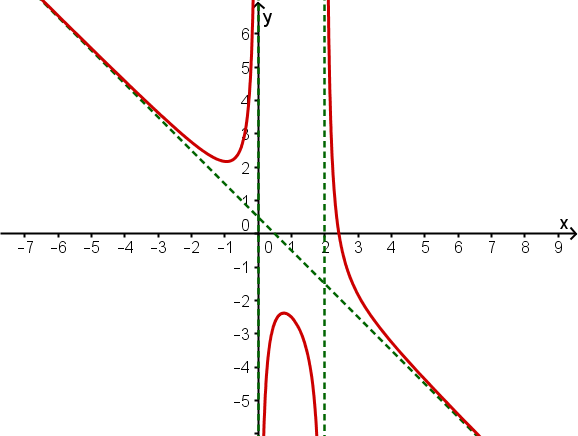
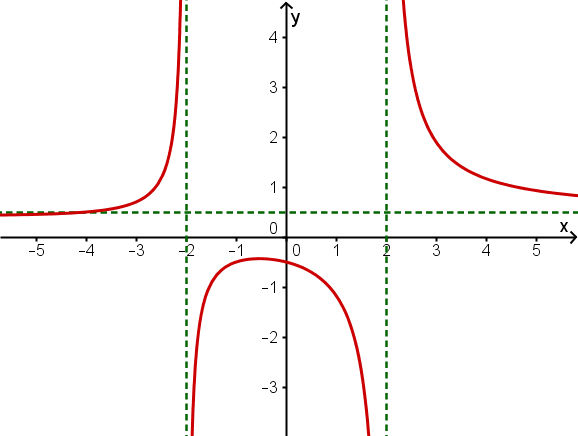
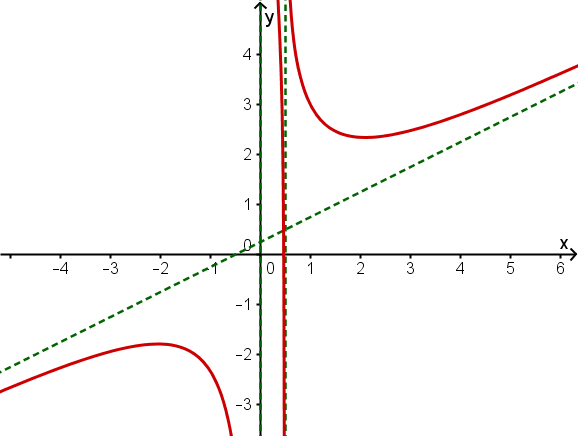
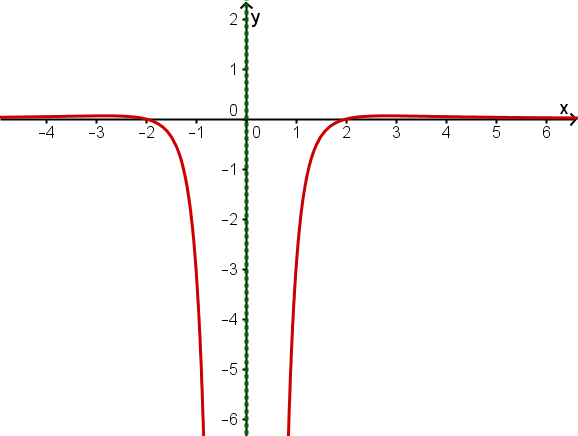
Gib den Term einer (möglichst einfachen) gebrochen rationalen Funktion f an, die folgende Eigenschaften besitzt.
Der Graph von berührt die x-Achse an der Stelle ;
die Funktion hat die Polstelle .
Der Graph von f hat eine Polstelle ohne Vorzeichenwechsel bei und für die Asymptote
Der Graph von f hat Polstellen mit Vorzeichenwechsel bei und und für die Asymptote
Der Graph von f hat eine Polstelle mit Vorzeichenwechsel bei , ist punktsymmetrisch zum Ursprung und hat für die Asymptote
Der Graph von f hat eine Polstelle bei und ist achsensymmetrisch zur y-Achse.
Für hat der Graph die Asymptote und bei befindet sich eine Nullstelle.
- 15
Gegeben ist die Funktion mit maximaler Definitionsmenge.
Gib die maximale Definitionsmenge an.
Weise nach, dass der Graph der Funktion achsensymmetrisch zur y-Achse ist.
Skizziere den Graphen der Funktion in ein Koordinatensystem.
Für welche Werte von unterscheiden sich die Funktionswerte der Funktion um weniger als vom Wert ?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?