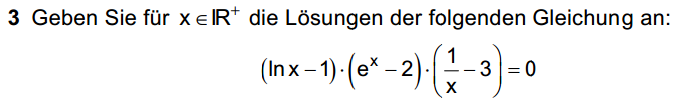Analysis I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Gegeben ist die Funktion mit maximaler Definitionsmenge D.
Bestimmen Sie und geben Sie die Nullstelle von an.
Ermitteln Sie die Gleichung der Tangente an den Graphen von im Punkt .
- 2
Geben Sie jeweils den Term einer in definierten Funktion an, die die angegebene Wertemenge hat.
- 3
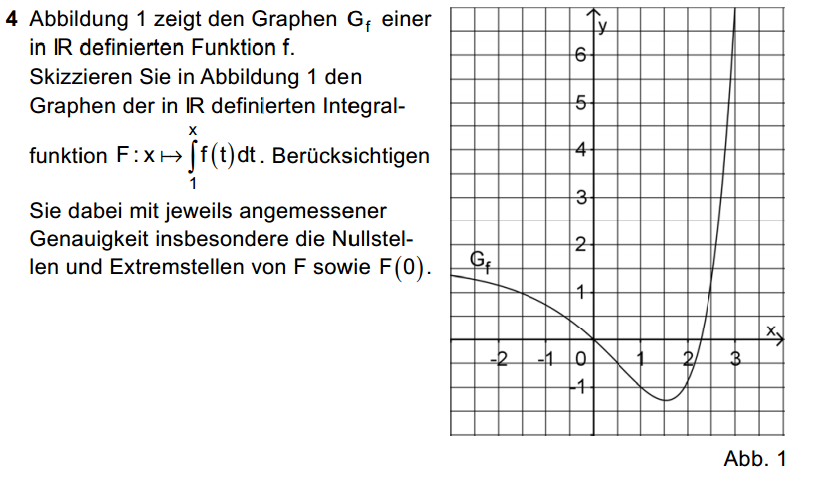
- 4
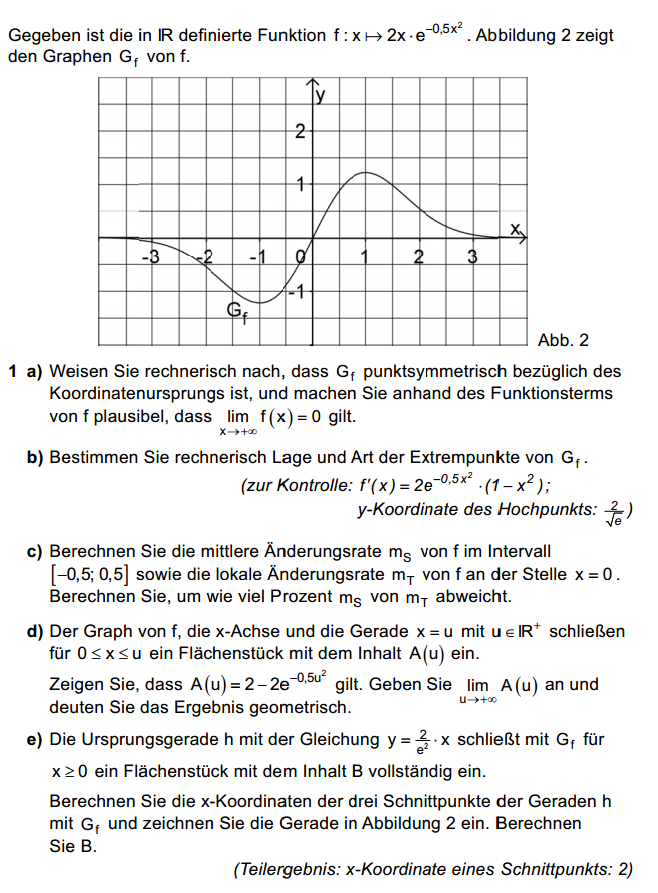
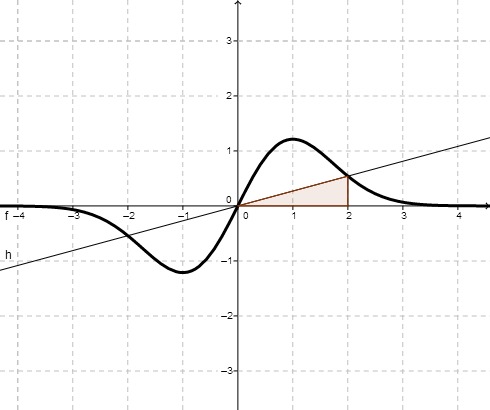
- 5
- 6
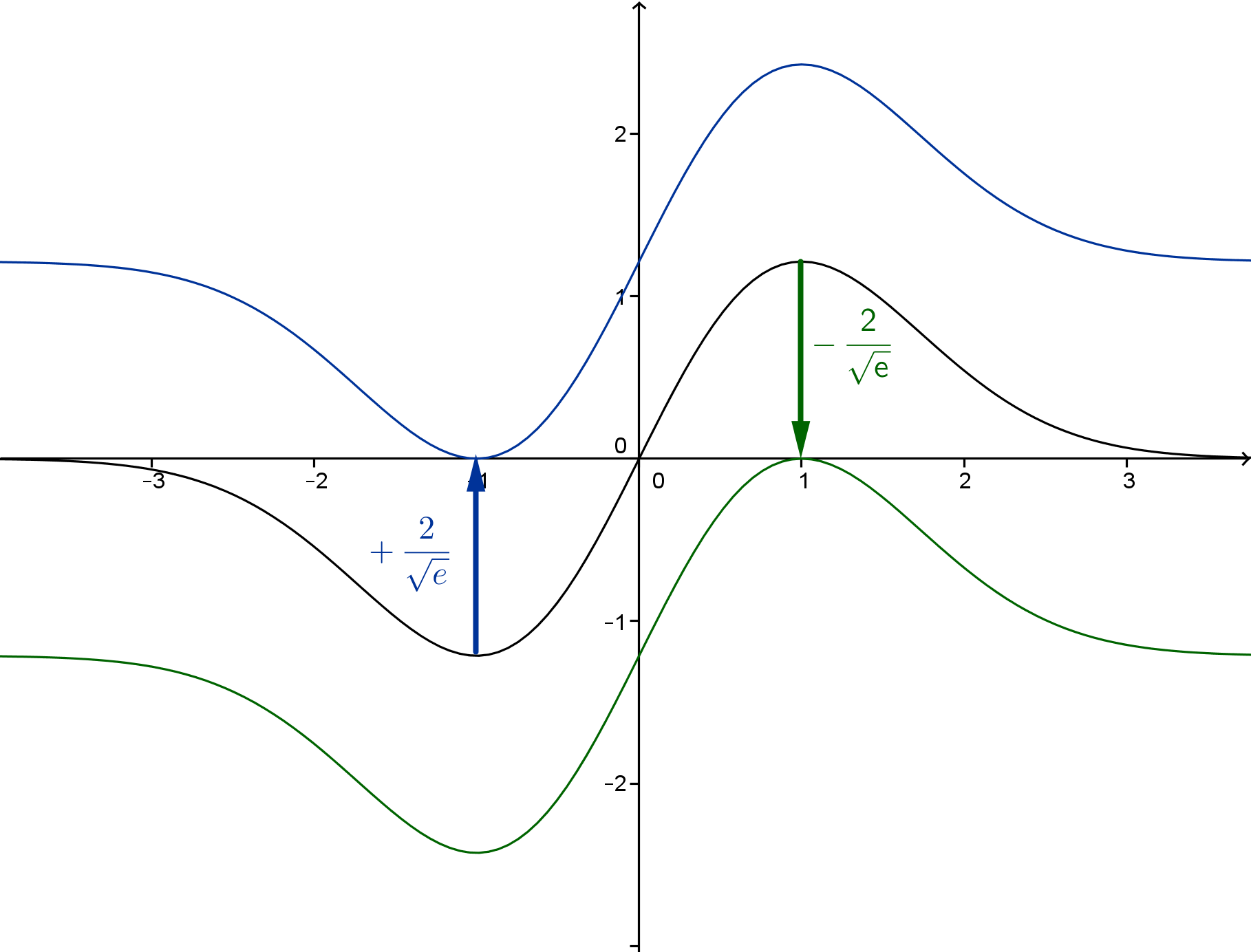
Im Folgenden wird die Schar der definierten Funktionen mit betrachtet.
Geben Sie in Abhängigkeit von c ohne weitere Rechnung die Koordinaten des Hochpunkts des Graphen von sowie das Verhalten von für
an.
Die Anzahl der Nullstellen von hängt von ab. Geben Sie jeweils einen möglichen Wert von an, sodass gilt:
a.) hat keine Nullstelle.
b.) hat genau eine Nullstelle.
c.) hat genau zwei Nullstellen.
Begründen Sie für anhand einer geeigneten Skizze, dass
gilt.
- 7
Die Anzahl der Kinder, die eine Frau im Laufe ihres Lebens durchschnittlich zur Welt bringt, wird durch eine sogenannte Geburtenziffer angegeben, die jedes Jahr statistisch ermittelt wird.
Die Funktion beschreibt für modellhaft die zeitliche Entwicklung der Geburtenziffer in einem europäischen Land. Dabei ist x die seit dem Jahr 1955 vergangene Zeit in Jahrzehnten (d. h. entspricht dem Jahr 1965) und () die Geburtenziffer. Damit die Bevölkerungszahl in diesem Land langfristig näherungsweise konstant bleibt, ist dort eine Geburtenziffer von etwa 2,1 erforderlich.
Zeichnen Sie den Graphen von in Abbildung 2 ein und ermitteln Sie graphisch mit angemessener Genauigkeit, in welchem Zeitraum die Geburtenziffer mindestens 2,1 beträgt.
Welche künftige Entwicklung der Bevölkerungszahl ist auf der Grundlage des Modells zu erwarten? Begründen Sie Ihre Antwort.
Im betrachteten Zeitraum gibt es ein Jahr, in dem die Geburtenziffer am stärksten abnimmt. Geben Sie mithilfe von Abbildung 2 einen Näherungswert für dieses Jahr an. Beschreiben Sie, wie man auf der Grundlage des Modells rechnerisch nachweisen könnte, dass die Abnahme der Geburtenziffer von diesem Jahr an kontinuierlich schwächer wird.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?