Aufgaben zu Wachstums- und Zerfallsprozessen
Hier findest du gemischte Aufgaben zu Wachstums- und Zerfallsprozessen. Lerne das Modellieren mit Wachstum und Zerfall!
- 1
Der Baumbestand eines Waldes in kann näherungsweise durch die Funktion beschrieben werden, wobei für die Anzahl vergangener Jahre seit der ersten Messung steht.
Begründe anhand des Funktionsterms, ob der Wald wächst oder schrumpft.
Berechne, wie groß der Wald in 10 Jahren ist.
Bestimme, wann der Wald groß ist.
Bestimme, vor wie vielen Jahren der Wald halb so groß war wie jetzt.
Bestimme, wie lange der Wald braucht, um seine Größe zu verdoppeln.
Vergleiche mit dem Ergebnis der vorherigen Teilaufgabe und formuliere dazu eine Aussage zur benötigten Zeit zum Verdoppeln der Waldgröße.
Häufig interessiert in Sachsituationen die Halbwerts- oder Verdopplungszeit einer Größe, also die Zeit, die benötigt wird, damit sich der Wert halbiert oder verdoppelt. Im Folgenden kannst du als Verdopplungszeit 7 Jahre annehmen.
Erkläre, warum der Wachstumsprozess des Waldes mit dieser Annahme näherungsweise auch mithilfe des Terms
beschrieben werden kann.
- 2
Bei einem radioaktiven Stoff zerfällt jedes Jahr 10% der noch vorhandenen Masse. Berechne, wie viel nach 10 Jahren noch vorhanden ist.
- 3
Modelliere jeweils durch einen entsprechenden Funktionsterm :
Die Tabelle zeigt die Entwicklung des ökologischen Landbaus in Deutschland:
Jahr
1984
1990
1996
2002
Fläche in 1000 ha
22
84
313
632
Falls die Entwicklung von 1990 bis 1996 durch eine Exponentialfunktion der Bauart beschrieben wird, wie lautet dann die Basis und wie ist dieser Wert zu interpretieren?
Überprüfe, ob die Daten von 1984 und 2002 zu dieser Modellierung passen.
Wann (in der Vergangenheit) startete nach diesem Modell die Fläche bei 0 ha?
Von einem radioaktiven Element sind anfangs 20 000 Atomkerne vorhanden, nach 183 Sekunden ist nur noch davon vorhanden.
Wann ist nur die Hälfte vorhanden (Halbwertszeit)?
Ein Hersteller von Bleistiften hat anfangs 20 000 Stifte in seinem Lager,
nach 183 Tagen ist (bei gleichmäßiger Nachfrage seitens der Kunden) nur noch davon vorrätig, wenn währenddessen keine Stifte produziert werden.
Ergibt sich eine lineare oder exponentielle Abnahme für Vorrat nach Tagen?
- 4
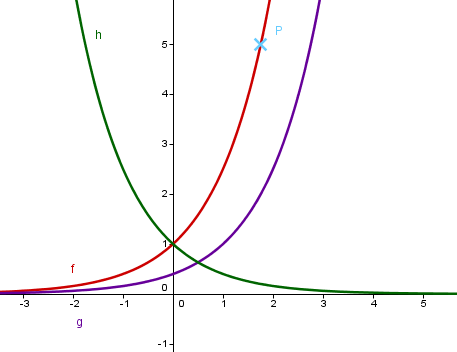
Zeichne mit Hilfe einer Wertetabelle die Graphen zu , und .
Vergleiche die Graphen.
Löse die Gleichung graphisch.
- 5
Herr Meier hat eine größere Summe Geld gewonnen und legt sie für 3 Jahre zu einem Zinssatz von 2% jährlich an. Nach 3 Jahren bekommt er von der Bank ausbezahlt.
Wie viel Geld hatte er angelegt?
- 6
Frau Müller hat gespart und legt sie für 5 Jahre zu einem festen Zinssatz an. Nach 5 Jahren bekommt sie ausbezahlt.
Zu welchem Zinssatz war das Geld angelegt?
- 7
Tante Luna zeigt ihrem 13-jährigen Neffen Luca ein Sparbuch, auf dem sich befinden. "Als du 8 Jahre alt warst", sagt sie, "hatte ich mir etwas Geld gespart und es zu einem festen Zinssatz angelegt. Wenn du 18 Jahre bist, bekommst du von mir ."
Wie viel Geld hatte Tante Luna angelegt und zu welchem Zinssatz?
- 8
Derzeit gibt es kein politisches System auf der Erde, das nicht auf Wirtschaftswachstum setzt. Wachstum gelten als wünschenswert und maßvoll: also jedes Jahr mehr im Vergleich zum Vorjahr. Um wie viel Prozent wäre also bei diesem Wachstum die Wirtschaft nach…
… 2 Jahren gewachsen?
… 10 Jahren gewachsen?
… 50 Jahren gewachsen?
- 9
Hans eröffnet am 1. Januar ein Konto und zahlt darauf ein.
Er erhält jährlich Zinsen, die er am Ende des Jahres jeweils auf das Konto gutschreiben lässt
Wie lautet der Kontostand nach 1, 2, 5 bzw. 10 Jahren?
Wie lange müsste Hans warten, damit sich sein Anfangskapital von verdoppelt hat?
- 10
Bakterien vermehren sich durch Teilung, wobei sich eine Bakterienzelle durchschnittlich alle 10 Minuten teilt. Zum Zeitpunkt sei genau eine Bakterienzelle vorhanden.
Wie viele Bakterien sind dann nach 1 Stunde, 2 Stunden, 6 Stunden, 12 Stunden bzw. 24 Stunden vorhanden?
Finde eine Formel für die Anzahl der Bakterien nach der Zeit .
Eine Bakterienzelle hat ein Volumen von ca. . Wie lange dauert es, bis die Bakterienkultur ein Volumen von bzw. einnimmt? Beurteile dein Ergebnis kritisch.
- 11
Ein Taucher interessiert sich wegen Unterwasseraufnahmen dafür, welche Helligkeit in verschiedenen Tiefen herrscht.
Messungen in einem bestimmten (recht trüben) See ergeben, dass die Helligkeit pro Meter Wassertiefe um ca. 17% abnimmt.
Für diese Aufgabe musst du dich mit exponentiellem Wachstum auskennen
allg. Formel
Abnahmefaktor
Anfangswert
Exponent= in Metern
in Prozent
Wie groß ist die Helligkeit in 1m, 2m, 5m bzw. 10m Tiefe, verglichen mit der Helligkeit an der Wasseroberfläche?
Beschreiben sie die Helligkeit H als Funktion der Wassertiefe x als Bruchteil der Helligkeit an der Wasseroberfläche.
In welcher Tiefe beträgt die Helligkeit weniger als ?
- 12
Beim Reaktorunglück von Tschernobyl wurde eine Menge von etwa radioaktiven Jod 131 freigesetzt.
Dieses Jod 131 hat eine sogenannte Halbwertszeit von 8,0 Tagen, d.h. in jeweils 8,0 Tagen halbiert sich die Menge des noch vorhandenen radioaktiven Materials Jod 131.
Allg. Formel:
Anfangswert a =
Zeit in Tagen
Wie kann man die Menge des radioaktiven Jods 131 als Funktion der Zeit angeben?
Welcher Prozentsatz der ursprünglich vorhandenen Menge war nach einem Tag bzw. nach 30 Tagen noch vorhanden?
Wie lange musste man etwa warten, bis von den 400g Jod 131 nur noch 1 Milligramm vorhanden war?
- 13
Bierschaumzerfall
Bei einer schlecht eingeschenkten Maß Bier beträgt die Schaumhöhe anfangs . Um das Bier einigermaßen trinken zu können, wartet der Gast eine gewisse Zeit. Nach 3 Minuten ist die Schaumhöhe auf die Hälfte zurückgegangen.
Stelle die Zerfallsgleichung für den Bierschaumzerfall auf.
Berechne, wann die Schaumhöhe auf zurückgegangen ist.
Bei einem anderen Gast beträgt die Schaumhöhe nach drei Minuten noch . Wie war die Schaumhöhe nach dem Einschenken?
Mache plausibel, wann der Zerfall am stärksten ist.
- 14
Für den Wasserverbrauch berechnet der Wasserversorger pro Wasser (Verbrauchskosten). Zusätzlich muss pro Monat eine Grundgebühr von bezahlt werden. Die monatlichen Gesamtkosten setzen sich aus den Verbrauchskosten und der Grundgebühr zusammen.
a) Zeichne den Graphen der Gesamtkostenfunktion:
Wasserverbrauch (in ) Gesamtkosten
b) Gib die Funktionsgleichung an.
c) Im Juli wurden Wasser verbraucht. Wie hoch ist die Wasserrechnung im Juli?
- 15
Eine Kerze ist anfangs lang. Beim Abbrennen wird sie stündlich um kürzer.
Zeichne den Graphen der Funktion:
Brenndauer (in Stunden) Länge der Kerze (Länge in)
Notiere die Funktionsgleichung.
Wie lang ist die Kerze nach 3 Stunden?
Wann ist die Kerze abgebrannt?
- 16
Die Bevölkerung einer Stadt wächst jährlich um . Im Jahr 2022 hat die Stadt 80000 Einwohner.
Wie lautet die Wachstumsfunktion mit dem Ansatz ?
Wie viele Einwohner wird die Stadt nach 15 Jahren haben?
Berechne die Verdopplungszeit.
Wann (nach Beobachtungsbeginn) beträgt die Wachstumsgeschwindigkeit etwa 400 Einwohner pro Monat?
- 17
Ein Sparer hat gespart. Sein Vermögen verliert durch die Inflation von zur Zeit jährlich an Wert.
Stelle die Gleichung für den Wert des Vermögens des Sparers auf (unter der Voraussetzung, dass sich die Inflationsrate nicht ändert):
Zeit (in Jahren) (in)
Wie hoch ist der Wert seines Vermögens nach 5 Jahren?
Wann ist sein Vermögen nur noch die Hälfte wert?
- 18
Beim Servieren von frisch gebrühtem Espresso hat dieser eine Temperatur von C.
Nach hat der Espresso nur noch eine Temperatur von C. Die Zimmertemperatur beträgt C.
Stelle die Gleichung für die beschränkte exponentielle Abnahme der Espressotemperatur auf.
Wie lange dauert es, bis die Espressotemperatur C beträgt?
- 19
Aus der Tiefkühltruhe wird ein gefrorenes Lebensmittel mit einer Temperatur von in die Küche zum Auftauen gebracht. Die Temperatur in der Küche beträgt . Nach hat sich das Tiefkühlgut auf erwärmt.
Bestimme die Funktionsgleichung für die beschränkte, exponentielle Zunahme.
Benutze dabei die allgemeine Funktionsgleichung für die beschränkte, exponentielle Zunahme:
Dabei ist:
: ist der Bestand zur Zeit ,
: ist die Sättigungsgrenze (Schranke)
: ist die Wachstumskonstante,
: ist der Anfangsbestand zur Zeit , also der Startwert.
Wie lange dauert es, bis sich das Tiefkühlgut auf erwärmt hat?
Zeichne den Graphen der Funktionsgleichung für .
Zeichne ebenfalls die Asymptote ein.
- 20
In der Abbildung ist eine logistische Wachstumsfunktion dargestellt. Entnimm der Abbildung die Funktionsgleichung und bestimme für die logistische Funktion die charakteristischen Parameter , und .
Schranke
Anfangswert
Wachstumskonstante
- 21
Ein Kind hat bei seiner Geburt eine Größe von . Nach Jahren ist das Kind groß. Als Erwachsener ist seine Größe .
Bestimme die logistische Wachstumsgleichung mit dem Ansatz:
Wann hat das Kind eine Größe von erreicht?
In welchem Jahr ist die Wachstumsgeschwindigkeit des Kindes am größten?
Das Wachstum gilt als abgeschlossen, wenn die jährliche Größenzunahme unter liegt. Wann ist das hier der Fall?
Wie sieht der Graph der Wachstumsfunktion aus?
- 22
Ein Wachstumsprozess für beschränktes exponentielles Wachstum einer Population wird durch eine Funktion beschrieben. bezeichnet die Anzahl der Individuen der Population zum Zeitpunkt ( in Jahren).
Zeichne mithilfe einer Wertetabelle die Wachstumsfunktion für .
Bestimme den Anfangswert des Bestandes und gib den Bestand nach Jahren an.
Bestimme die Schranke .
Nach welcher Zeit ist der aktuelle Bestand auf von angewachsen?
- 23
In einem Dorf mit Einwohnern breitet sich eine Grippewelle aus. Die Grippewelle soll auf das Dorf beschränkt bleiben. Anfangs waren nur Personen infiziert. Nach einer Woche waren schon Personen an Grippe erkrankt.
Wie lautet die logistische Wachstumsfunktion für die Zahl der an Grippe Erkrankten?
Wie sieht der zugehörige Graph aus?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?