Aufgaben zum Rechnen mit Brüchen und Dezimalbrüchen
Hier findest du gemischte Übungsaufgaben zum Rechnen mit Brüchen und Dezimalbrüchen. Schaffst du sie alle?
- 1
Berechne den Wert des Terms .
- 2
Untersuche, ob die Summe aus einem echten Bruch und seinem Kehrbruch ergeben kann.
- 3
Untersuche, ob der Quotient aus einem unechten Bruch und seinem Kehrbruch ergeben kann.
- 4
Welche Zahl ergibt durch ihren 6. Teil geteilt den Wert 6?
- 5
Welche Zahl ergibt durch ihren 6. Teil geteilt den Wert 5?
- 6
Berechne x am Rechteck ABCD. (Die Zeichnung ist nicht maßstabgerecht.)
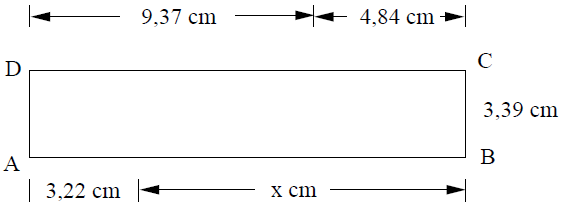 cm
cm - 7
Berechne ein Viertel von .
- 8
Berechne fünf Hundertstel von 0,2.
- 9
Berechne
- 10
Manfred schreibt:" "
Was meinst du dazu?
- 11
Wandle in Kilogramm um und rechne. (1 dz = 100kg)
- 12
Berechne die Doppelbrüche.
- 13
Welche Fehler wurden hier gemacht? Verbessere!
- 14
Vergleiche
- 15
Berechne.
- 16
Gegeben ist der Term: .
Gliedere den Term und berechne seinen Wert.
Wie ändert sich der Wert des Terms, wenn man durch ersetzt?
- 17
Gegeben ist der Term .
Berechne den Wert des Terms.
Setze zweimal Klammern so, dass der Wert des Terms beträgt.
- 18
Berechne den Wert des Terms.
- 19
Gegeben ist der Term .
Berechne den Wert des Terms.
Wird der Wert des Terms größer oder kleiner, wenn man die Hochzahl bei weglässt? Begründe deine Antwort, ohne erneut zu rechnen.
- 20
Gegeben ist der Term .
Berechne den Wert des Terms.
Setze eine Klammer so, dass der Wert des neuen Terms Null ist.
- 21
Gegeben ist der Term .
Berechne den Wert des Terms.
Setze eine weitere Klammer so, dass man den Wert des Terms sofort im Kopf bestimmen kann.
- 22
Gegeben ist der Term .
Gliedere den Term und berechne seinen Wert.
Ist es möglich, ein Rechenzeichen durch ein anderes so zu ersetzen, dass der Termwert größer wird?
- 23
Gegeben ist der Term .
Berechne den Wert des Terms.
Wird sein Wert größer oder kleiner, wenn man durch ersetzt? Begründe deine Antwort, ohne erneut zu rechnen.
- 24
Gegeben ist der Term .
Berechne den Wert des Terms.
Peter behauptet: „Die erste Klammer kann man weglassen, ohne dass sich am Ergebnis etwas ändert!“ Hat Peter Recht?
- 25
Wandle den Dezimalbruch in einen Bruch um und kürze, wenn möglich.
(Eingabeform: a/b, z.B. 1/2 für 0,5)
0,75
0,6
2,5
3,25
0,8
0,7
0,74
0,25
1,53
0,007
0,7456
0,95
0,28
0,085
0,39
- 26
Löse die folgenden Aufgaben.
Berechne den Wert des Terms
Wenn man im Minuenden nicht durch dividiert, sondern stattdessen mit multipliziert, ändert sich der Wert des Terms. Entscheide ohne erneute Rechnung, ob der Wert des Terms dabei größer oder kleiner wird.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
