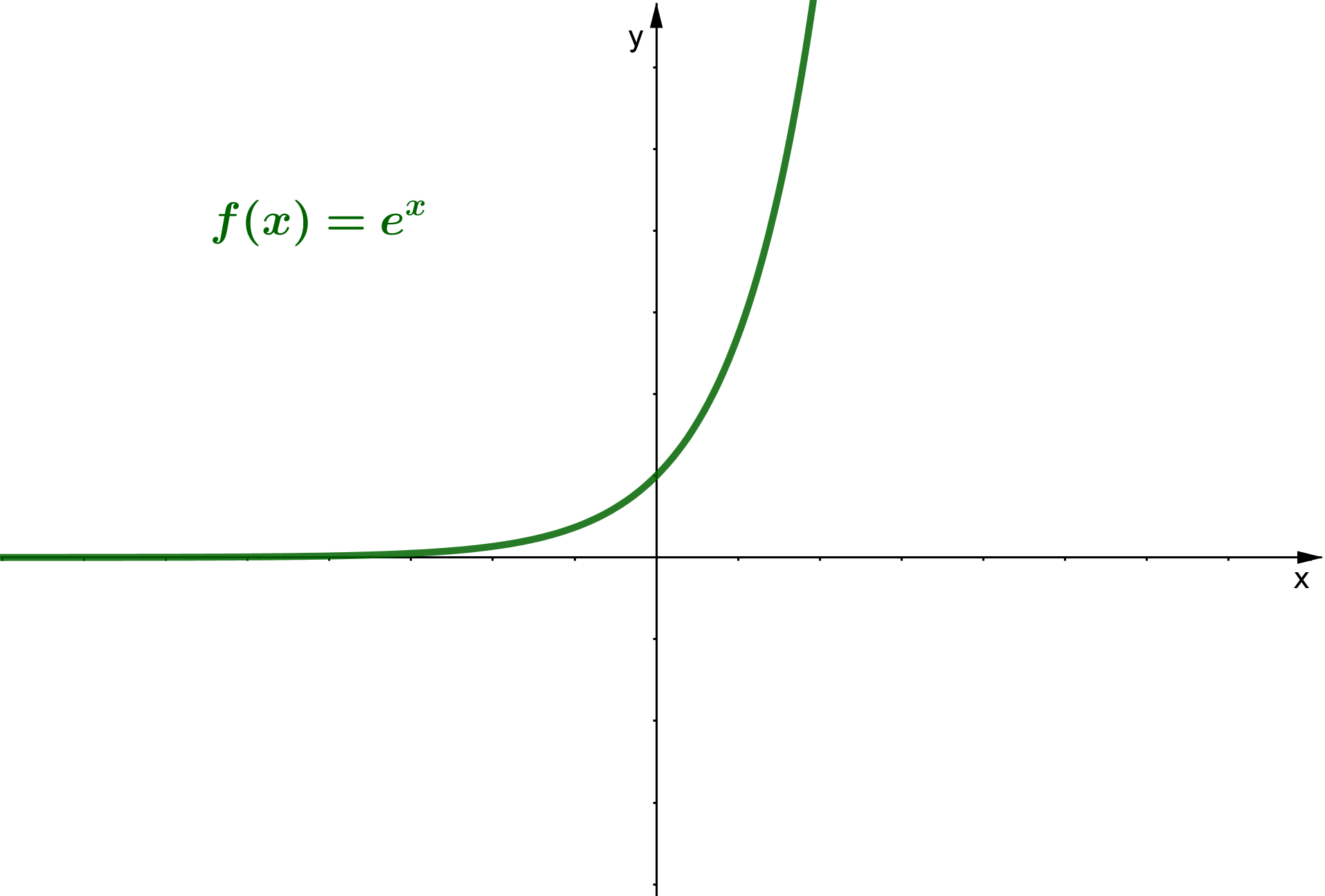1 Übersicht
In diesem Kurs lernst du, wie du vorgehen kannst, um den Definitionsbereich ausgewählter Funktionen bestimmen zu können.
Das solltest du bereits können
Gleichungen und Ungleichungen umformen
Nullstellen berechnen
Grundkenntnisse über die verschiedenen Funktionstypen
Kursdauer
ca. 2 Stunden
2 Der Definitionsbereich
Der Definitionsbereich (auch Definitionsmenge genannt) ist die Menge von Zahlen, die man in eine Funktion einsetzen darf. Das Zeichen für diese Menge ist .

bestimmst du, indem du untersucht, ob einzelne Teile des Funktionsterms für bestimmte Zahlenbereiche nicht definiert sind, also ob es Zahlen gibt, die du nicht in die Funktion einsetzen darfst. Zahlen aus diesen Bereichen musst du aus der Definitionsmenge herausnehmen.
Ausdrücke, die nicht auf ganz definiert sind, können z. B. sein:
Brüche (sind nur definiert, wenn der Nenner ungleich Null ist)
Wurzeln (sind nur für Zahlen größer gleich Null definiert)
Logarithmen (sind nur für positive Zahlen definiert)
Die Menge hängt von der Funktion ab, die du betrachtest. Auf den folgenden Kursseiten werden dir die unterschiedlichen Typen von Funktionen vorgestellt und ihre Definitionsmengen betrachtet.
3 Definitionsbereich von Polynomfunktionen
Eine Polynomfunktion ist eine Funktion der Form mit aus und .
Zum Beispiel: .
Der Defintionsbereich von Polynomfunktionen ist, falls nicht anders angegeben, ganz . Das heißt man darf alle Zahlen ohne Ausnahme einsetzen, also .
Warum? Man kann beim Einsetzen von bestimmten Werten in eine ganzrationale Funktion keine mathematischen Gesetze verletzen, da keine Bruchterme, Wurzeln und Logarithmen vorkommen.
Beispiele
Normalparabel:
quadratische Funktionen:
kubische Funktionen:
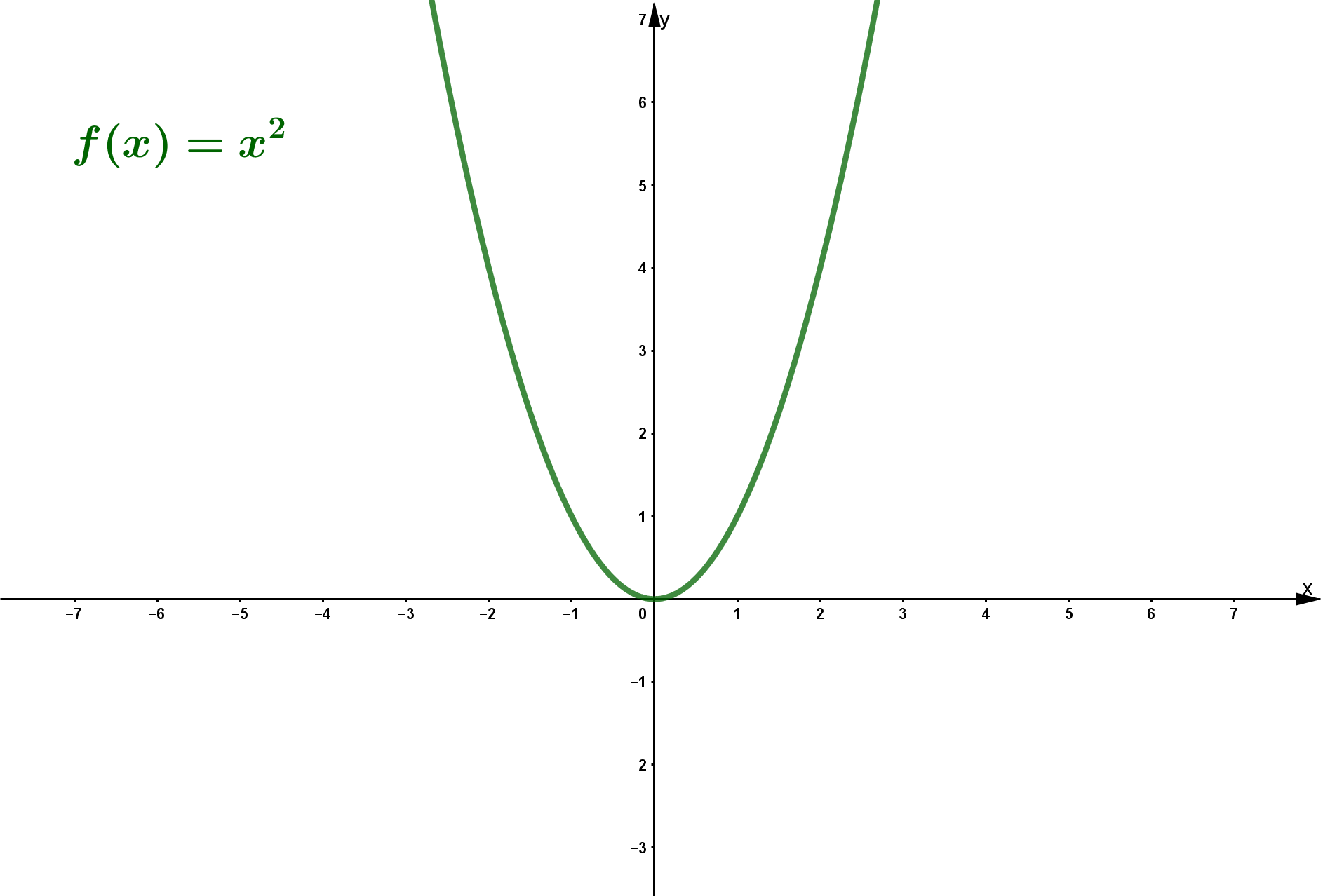
4 Definitionsbereich gebrochen-rationaler Funktionen
Eine gebrochen-rationale Funktion ist eine Funktion, die sich als Bruch von Polynomen darstellen lässt. Gebrochen-rationale Funktionen sind also von der Form , wobei sowohl als auch Polynome sind.
Da man nicht durch Null teilen darf, muss man alle Zahlen ausschließen, für die gilt: Der Nenner .
Beispiel
Prüfe, wann Null wird.
| ↓ | ausklammern. | ||
| ↓ | Verwende: Ein Produkt wird Null, wenn einer der Faktoren Null ist. Setze die einzelnen Faktoren gleich Null. | ||
Die Nullstellen sind gegeben durch: , und .
Man muss diese drei Werte aus der Definitionsmenge ausschließen, also .
5 Übungsaufgaben
Gib für folgende Funktionen den Definitionsbereich an.
a)
Laden
b)
Laden
c)
Laden
d)
Laden
6 Definitionsbereich von Wurzelfunktionen
Wurzelfunktionen sind Potenzfunktionen in der Form, dass die Variable unter einer Wurzel steht, also . Sie bilden damit die Umkehrfunktionen zu Potenzfuktionen der Form mit .
Bemerkung: ist keine Wurzelfunktion, da keine Variable (hier: ) unter der Wurzel steht.
Man muss darauf achten, dass unter geraden Wurzeln kein negativer Wert als Radikand (Term unter der Wurzel) steht.
Beispiel
| ↓ | Prüfe, wann der Radikand kleiner Null wird. | ||
Das Intervall muss man also aus dem Definitionsbereich ausschließen.
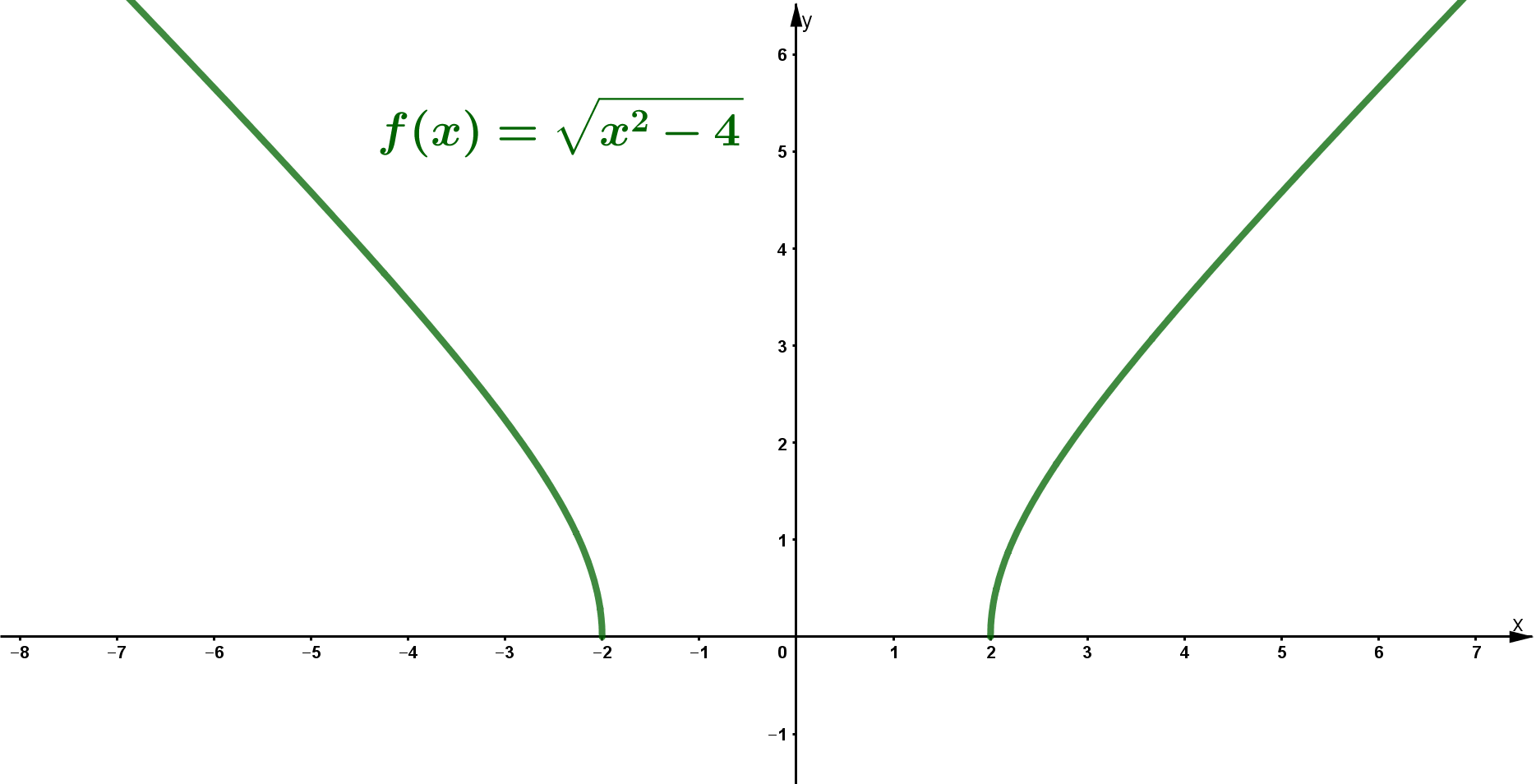
7 Übungsaufgaben
Gib für folgende Funktionen den Definitionsbereich an.
a)
Laden
b)
Laden
c)
Laden
d)
Laden
8 Definitionsbereich von Exponentialfunktionen
Eine Exponentialfunktion hat den Funktionsterm . Dabei ist und .
Der Defintionsbereich von Exponentialfunktionen ist, falls nicht anders angegeben, ganz . Das heißt man darf alle Zahlen ohne Ausnahme einsetzen, also .
Warum? Man kann beim Einsetzen von bestimmten Werten in eine Exponentialfunktion keine mathematischen Gesetze verletzen, da keine Bruchterme, Wurzeln und Logarithmen vorkommen.
Beispiele
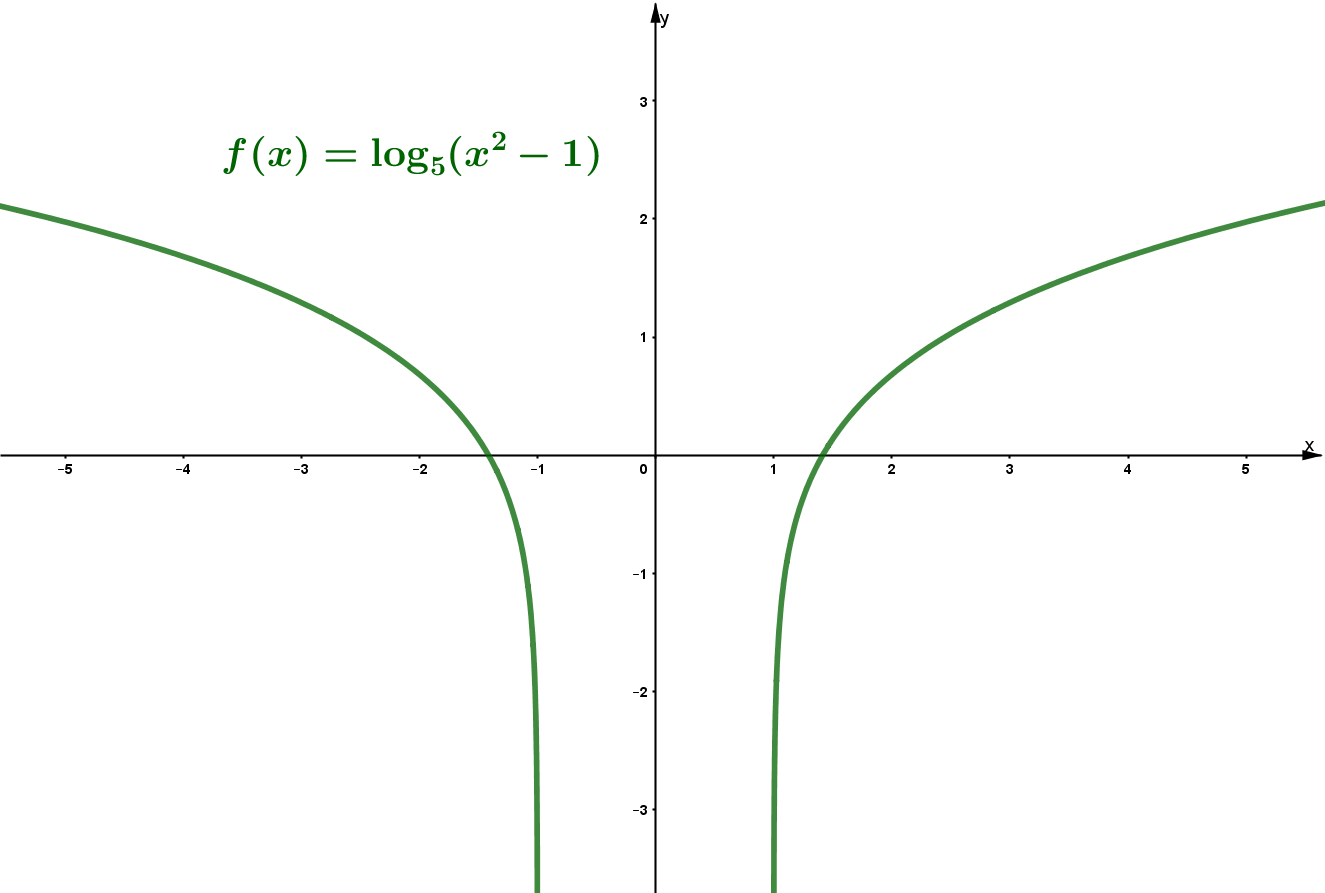
9 Definitionsbereich von Logarithmusfunktionen
Eine Logarithmusfunktion ist eine Abbildung mit der Funktionsvorschrift
, wobei und gilt.
heißt Basis des Logarithmus und das Argument des Logarithmus.
Das Argument kann auch ein Term beliebiger Form sein.
Bei Logarithmusfunktionen muss man darauf achten, dass das Argument stets positiv wird.
Beispiel
Prüfe, wann das Argument kleiner oder gleich Null wird.
Wichtig bei der Umformung ist, den Betrag nicht zu vergessen!
Wenn zwischen und liegt, wird kleiner oder gleich . Das Intervall von bis muss man also ausschließen.
10 Übungsaufgaben
Gib für folgende Funktionen den Definitionsbereich an.
a)
Laden
b)
Laden
c)
Laden
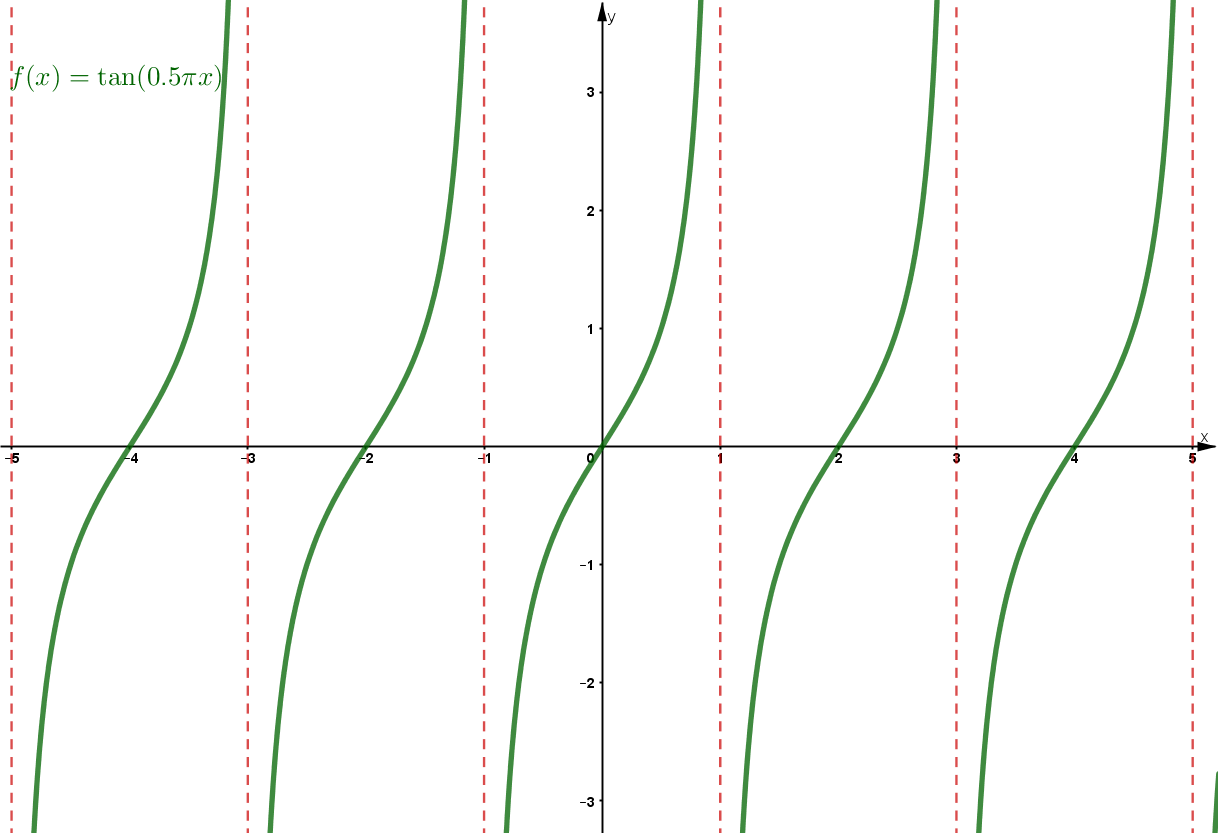
11 Definitionsbereich von trigonometrischen Funktionen
Sinus- und Kosinusfunktion haben ganz als Definitionsbereich.
Die Tangensfunktion ist folgendermaßen definiert: .
Man sieht, dass man alle ausschließen muss, für die wird. Dies ist für die folgende Zahlenmenge der Fall: . Vergleiche hierzu auch die Kursseite "Nullstellen von trigonometrischen Funktionen (3/5)".
Im Definitionsbereich der Tangensfuntion müssen somit alle ausgeschlossen werden, für die das Argument gleich mit wird.
Beispiel
Prüfe, wann das Argument gleich mit wird.
Die Werte mit müssen somit aus der Definitionsmenge ausgeschlossen werden.
.
12 Übungsaufgaben
Gib für folgende Funktionen den Definitionsbereich an.
a)
Laden
b)
Laden
c)
Laden
13 Zusammenfassung
Der Definitionsbereich (auch Definitionsmenge genannt) ist die Menge von Zahlen, die man in eine Funktion einsetzen darf. Das Zeichen für diese Menge ist .
Die Definitionsmenge hängt von der Funktion ab:
Für Polynomfunktionen und Exponentialfunktionen gilt:
Bei einer gebrochenrationalen Funktion darf der Nenner nicht Null werden.Setze das Nennerpolynom und schließe dessen Nullstellen aus dem Definitionsbereich aus.
Bei Wurzelfunktionen darf der Radikand nicht negativ werden. Prüfe, wann der Radikand kleiner Null wird und schließe das Ergebnis aus der Definitionsmenge aus.
Bei Logarithmusfunktionen muss das Argument stets positiv sein. Prüfe, wann das Argument kleiner oder gleich Null wird und schließe das Ergebnis aus dem Definitionsbereich aus.
Für die Sinus- und Kosinusfunktion gilt: .
Bei der Tangensfunktion müssen die Nullstellen der Kosinusfunktion aus dem Definitionsbereich ausgeschlossen werden. Setze dazu das Argument gleich mit und löse nach auf.
Einen kurze Überblick, was du beim Bestimmen des Definitionsbereichs beachten musst, findest du im Artikel Definitionsbereich bestimmen.
14 Kann ich's?
Gib für folgende Funktionen den Definitionsbereich an.
a)
Laden
b)
Laden
c)
Laden
d)
Laden
Die Aufgaben aus diesem Kurs und noch weitere Übungsaufgaben zum Definitionsbereich findest du hier.