Aufgaben zu linearen Funktionen
- 1
Berechne die Steigung der Gerade durch die gegebenen Punkte.
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
Setze die Punkte in den Differenzenquotient für die Gerade ein.
Die Steigung der Geraden beträgt .
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
Setze die Punkte in den Differenzenquotient für die Gerade ein.
Die Steigung der Geraden beträgt m = 1.
Hast du eine Frage oder Feedback?
- 2
Stelle die Gleichung der Geraden durch die Punkte und auf.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Gegeben sind die beiden Punkte und .
Gesucht ist die Gleichung der Geraden, die durch die beiden Punkte geht.
Zur Ermittlung der Geradengleichung überlegst du am Besten erst die allgemeine Form der Geradengleichung:
Bestimmung der Steigung
Erinnere dich zunächst an die Gleichung für die Steigung einer Geraden:
Setze die Werte aus den Punkten und in die Formel ein.
Jetzt weißt du, dass die Gleichung der Geraden durch die Punkte und geht folgendermaßen aussieht:
Als nächstes ermittelst du den -Achsenabschnitt ().
Ermittlung des -Achsenabschnitts
Um zu ermitteln setzt du den - und -Wert einer der beiden Punkte in die Geradengleichung ein. Hier wird das beispielhaft mit dem Punkt ausgerechnet.
Der -Achsenabschnitt der Funktion ist . Damit hast du auch schon die ganze Funktionsgleichung.
- 3
Welche Steigung hat die Gerade durch die Punkte und ? Wie lautet also die Funktionsgleichung?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Steigung
Bestimme die Steigung .
Setze die beiden Punkte in die Formel für die Steigung ein.
Funktionsgleichung
Bestimme die Funktionsgleichung.
Setze m in die allgemeine Geradengleichung ein.
Setze einen der beiden Punkte in die Funktionsgleichung ein.
Setze t in die Funktionsgleichung ein.
- 4
Bestimme die Gleichung der Geraden, die durch den Punkt P geht und senkrecht zur gegebenen Gerade steht.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu senkrechten Geraden mit der Formel.
Setz den Wert ein.
Die gesuchte Senkrechte hat also Steigung .
Bestimme nun den y-Achsenabschnitt der Senkrechten mit dem gegebenen Punkt , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
Setze die Werte ein.
Vereinfache und addiere .
Also lautet die gesuchte Geradengleichung .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu senkrechten Geraden mit der Formel.
Setz den Wert ein.
Die gesuchte Senkrechte hat also Steigung .
Bestimme nun den y-Achsenabschnitt der Senkrechten mit dem gegebenen Punkt , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
Setz die Werte ein.
Vereinfache und addiere 2.
Also lautet die gesuchte Geradengleichung .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu senkrechten Geraden mit der Formel.
Setz den Wert ein.
Die gesuchte Senkrechte hat also Steigung .
Bestimme nun den y-Achsenabschnitt der Senkrechten mit dem gegebenen Punkt , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
Setz die Werte ein.
Vereinfache und addiere 2.
Also lautet die gesuchte Geradengleichung .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu senkrechten Geraden mit der Formel.
Setz den Wert ein.
Die gesuchte Senkrechte hat also Steigung .
Bestimme nun den y-Achsenabschnitt der Senkrechten mit dem gegebenen Punkt , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
Setz die Werte ein.
Vereinfache und addiere 0,5.
Also lautet die Geradengleichung .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu senkrechten Geraden mit der Formel.
Setz den Wert ein.
Die gesuchte Senkrechte hat also Steigung .
Bestimme nun den y-Achsenabschnitt der Senkrechten mit dem gegebenen Punkt , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
Setz die Werte ein.
Vereinfache und subtrahiere 6.
Also lautet die Geradengleichung .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu senkrechten Geraden mit der Formel.
Setz den Wert ein.
Die gesuchte Senkrechte hat also Steigung .
Bestimme nun den y-Achsenabschnitt der Senkrechten mit dem gegebenen Punkt , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
Setz die Werte ein.
Vereinfache und addiere 6.
Also lautet die Geradengleichung .
Hast du eine Frage oder Feedback?
- 5
Bestimme die Gleichung der Geraden, die durch …
den Punkt geht und parallel ist zur -Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur -Achse, das heißt die gleiche Steigung wie die -Achse, also .
und in die allgemeine Geradengeleichung einsetzen.
Zur Geradengleichung zusammensetzen.
Hast du eine Frage oder Feedback?
den Punkt geht und parallel ist zur Winkelhalbierenden des 2.Quadranten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur Winkelhalbierenden des 2. Quadranten bedeutet gleiche Steigung.
Die Steigung der Winkelhalbierenden des 2. Quadranten ist -1
in die Geradengleichung einsetzen und damit berechnen.
und in die allgemeine Geradengleichung einsetzen.
Hast du eine Frage oder Feedback?
den Punkt geht und parallel ist zur -Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur -Achse, d.h. keine Funktionsgleichung, da einem -Wert unendlich viele -Werte zugeordnet werden. Die Gerade kann also nur als der -Wert von beschrieben werden.
Hast du eine Frage oder Feedback?
den Punkt geht und parallel ist zur Winkelhalbierenden des 1.Quadranten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur Winkelhalbierenden des 1. Quadranten bedeutet die gleiche Steigung.
Die Steigung der Winkelhalbierenden des 1. Quadranten ist 1.
Setze m und S in die allgemeine Geradengleichung ein und löse nach auf.
Setze und in die allgemeine Geradengleichung ein.
Hast du eine Frage oder Feedback?
den Ursprung geht und parallel ist zur Geraden mit und .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Durch den Ursprung, das heißt -Achsenabschnitt
Parallel zur Geraden , bedeutet die gesuchte Gerade hat die gleiche Steigung wie .
Berechne die Steigung mithilfe des Differenzenquotienten .
Setze und in die allgemeine Geradengleichung ein.
Hast du eine Frage oder Feedback?
- 6
Bestimme von folgenden Geraden die Schnittpunkte mit den Koordinatenachsen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Klammer auflösen
Um eine allgemeine Geradengleichung zu erhalten, multipliziere die Klammer aus.
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein und löse nach auf.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Gleichung umstellen
Um eine allgemeine Geradengleichung zu erhalten, vertausche auf der rechten Seite beide Elemente.
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
- 7
Stelle die Funktionsgleichung für die Gerade durch die Punkte P(-25|30) und Q(55|-30) auf und berechne den Schnittpunkt der Gerade mit der x-Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung ermitteln
P(-25|30); Q(55|-30)
Ermittle die Steigung m der allgemeinen Geradengleichung mithilfe des Differenzenqotienten .
Setze m und die Koordinaten eines Punktes z. B. P(-25|30) in die allgemeine Geradengleichung ein.
Vereinfache:
↓ Löse nach t auf.
↓ Setze m und t in die allgemeine Geradengleichung ein.
An der Schnittstelle mit der x-Achse ist der y-Wert 0.
Nach x auflösen. Stelle dafür das x alleine durch:
Beachte, dass bei beide Summanden multipliziert werden müssen.
Addiere 15
Die Gerade schneidet die x-Achse bei S(15|0).
- 8
Eine Gerade durch schließt mit den Koordinatenachsen ein Dreieck ein.
Für welche Steigung ist dieses Dreieck gleichschenklig?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Dreieck
Zwei Seiten des Dreiecks sind Koordinatenachsen. Diese haben einen rechten Winkel zwischen sich, das Dreieck ist also sicher rechtwinklig. Der rechte Winkel kann kein Basiswinkel im gleichschenkligen Dreieck sein, also sind die gleichlangen Schenkel die Katheten (Achsen).
Es gibt zwei Möglichkeiten einen Punkt zu wählen, dass die Katheten gleichlang sind: und . Das Dreieck liegt dann im 1. Quadranten oder im 4. Quadranten. In anderen Quadranten kann das Dreieck nicht liegen, da P auf der Grenze zwischen dem ersten und vierten liegt.
Damit erhältst du ein Steigungsdreieck für mit der Steigung und eines für mit der Steigung .
Ein solches Dreieck tritt also für die Steigungen und auf.
- 9
Funktionsgleichung bestimmen.
Eine Gerade hat die Steigung und verläuft durch den Punkt P. Bestimmen Sie die Funktionsgleichung f(x), die Achsenschnittpunkte und zeichnen Sie den Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Allgemeine Geradengleichung:
hier ist
↓ Setze in die allgemeine Geradengleichung ein.
↓ Setze P in f(x) ein.
↓ löse nach t auf
↓ Setze t in f(x) ein.
Bestimmung des Schnittpunkts mit der y-Achse
Gesucht ist der sogenannte y-Achsenabschnitt (hier: t), also wo und ist.
Da die allgemeine Geradengleichung
lautet, gilt immer für
.
Hier ist
Schnittpunkt mit der y-Achse bei
Bestimmung des Schnittpunkts mit der x-Achse
↓ Gesucht ist hier ein x mit f(x) =0 und somit y=0 ist. Setze Funktionsgleichung gleich 0.
↓ Du dividierst durch einen Bruch Multipliziere mit dem Kehrwert.
Schnittpunkt mit der x-Achse bei
Zeichnung
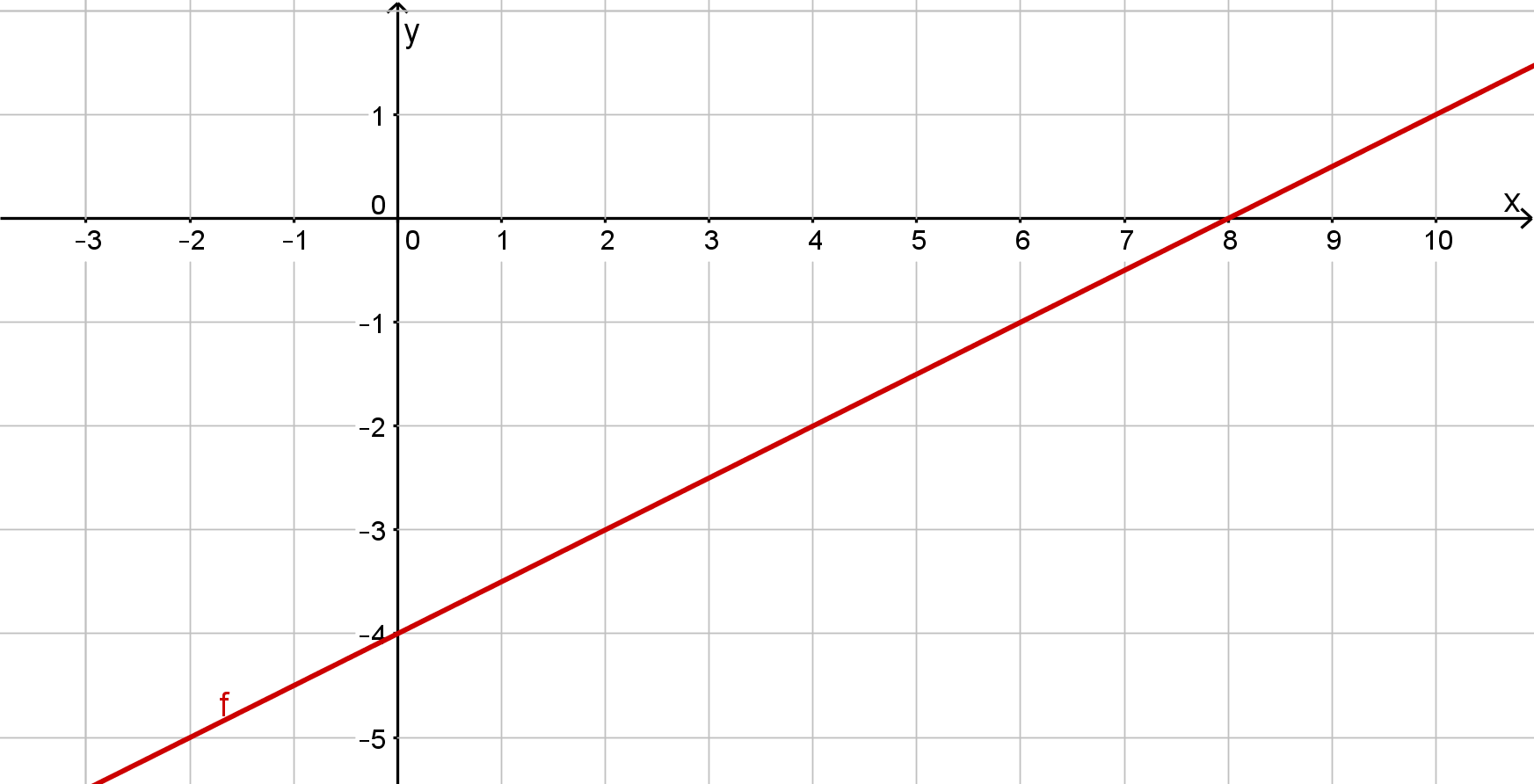
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Allgemeine Geradengleichung:
↓ t: y-Achsenabschnitt
Setze in die allgemeine Geradengleichung ein.
↓ Setze P(1/-3) in f(x) ein.
↓ ↓ ↓ Setze t in f(x) ein.
Bestimmung der Achsenschnittpunkte
Setze , um die Nullstellen zu bestimmen.
↓ Du dividierst durch einen Bruch Multipliziere mit dem Kehrwert.
↓ Also ist der Schnittpunkt mit der x-Achse bei
Der y-Achsenabschnitt entspricht dem Schnittpunkt mit der y-Achse.
Der Schnittpunkt mit der y-Achse ist bei
Zeichung
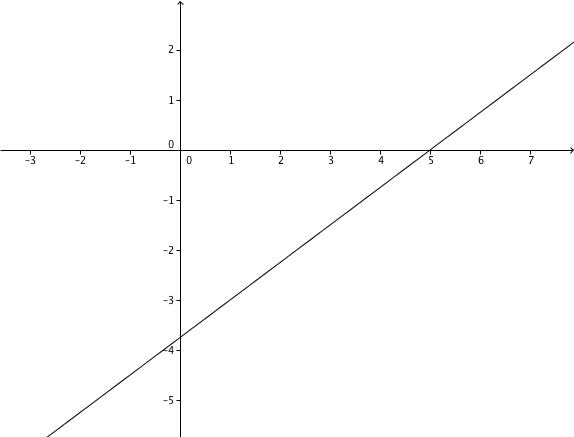
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Allgemeine Geradengleichung: Hier mit
↓ t: y-Achsenabschnitt
Setze in die allgemeine Geradengleichung ein.
↓ Setze P(3/-1) in f(x) ein.
↓ ↓ ↓ Setze t in f(x) ein.
Bestimmung der Achsenschnittpunkte
Setze , um die Nullstellen zu bestimmen.
Der Schnittpunkt mit der x-Achse bei .
Der y-Achsenabschnitt entspricht dem Schnittpunkt mit der y-Achse.
Schnittpunkt mit der y-Achse bei
Zeichnung
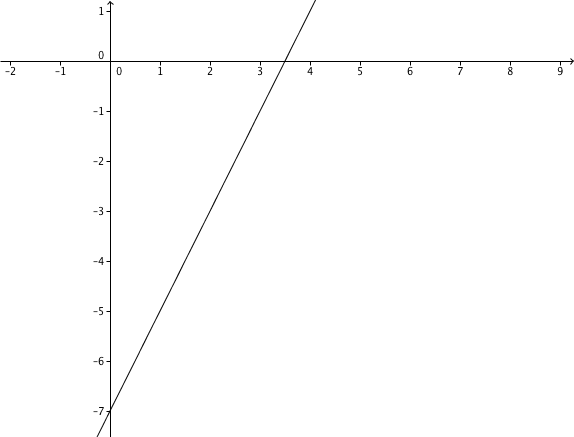
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Allgemeine Geradengleichung:
↓ t: y-Achsenabschnitt
Setze in die allgemeine Geradengleichung ein.
↓ Setze in f(x) ein.
↓ Kürze den Bruch mit 2.
↓ ↓ Schreibe 4 als Bruch mit 4 im Nenner.
↓ ↓ Setze t in f(x) ein.
Bestimmung der Achsenschnittpunkte
Setze , um die Nullstellen zu bestimmen.
Der Schnittpunkt mit der x-Achse bei
Der y-Achsenabschnitt entspricht dem Schnittpunkt mit der y-Achse.
Hier ist
Schnittpunkt mit der y-Achse bei .
Zeichnung
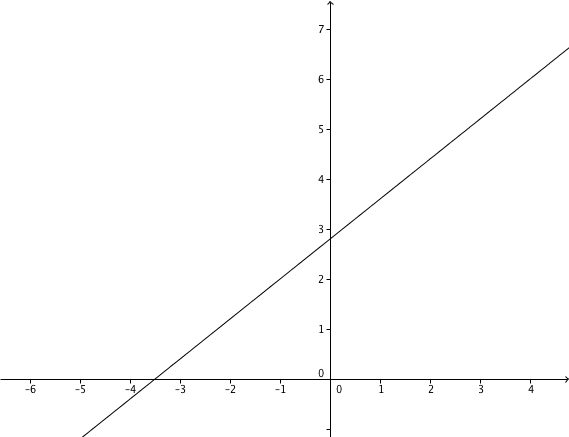
Hast du eine Frage oder Feedback?
- 10
Bestimme die Gleichung folgender Gerade:
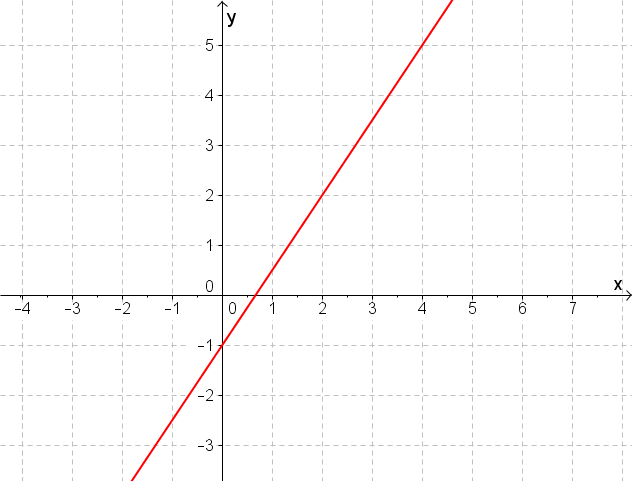
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Die allgemeine Geradengleichung ist:
Lese den y-Achsenabschnitt , also die Stelle, an der die Gerade die y-Achse schneidet, aus der Zeichnung ab.
Suche zwei Punkte mit (bestenfalls) ganzzahligen Koordinaten.
und liegen auf der Gerade.
Um die Steigung zu bestimmen, gibt es zwei Möglichkeiten:
1.
Setze die Koordinaten von und ein!
2.
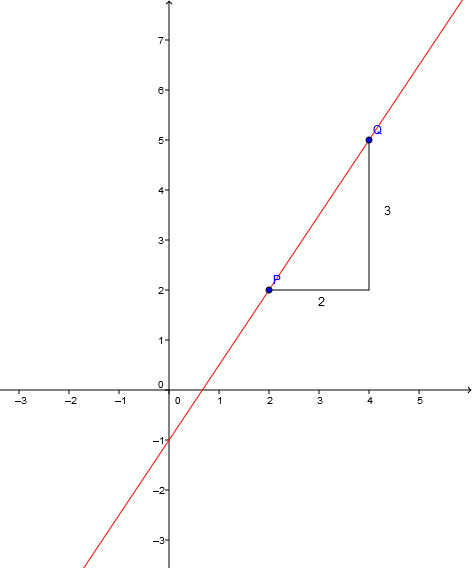
Zeichne ein Steigungsdreieck zwischen den Punkten. Der senkrechte Abstand ist der Zähler, der waagerechte Abstand ist der Nenner des Bruches, der die Steigung beschreibt.
Die Geradengleichung ist also gegeben durch:
- 11
Stelle die Gleichung der Geraden mit Steigung durch den Punkt auf und zeichne sie in ein Koordinatensystem.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung erstellen
↓ ↓ Bringe die beiden Brüche auf denselben Nenner.
↓ ↓ Wandle in einen gemischten Bruch um.
↓ Setze t und m in die allgemeine Geradengleichung ein.
Gerade zeichnen
Wähle einen beliebigen Punkt auf der Geraden, z. B. den gegebenen Punkt . Einen zweiten Punkt findest du, indem du vom Punkt aus entsprechend der Steigung , um nach rechts und um nach unten gehst. Du erhältst das . Verbinde die beiden Punkte zu einer Geraden.
Einfacher findest du den zweiten Punkt, indem du um nach rechts und nach unten gehst. Du erhältst das . (Die Steigung ist dann immer noch .)
- 12
Zeichne die Geraden und in ein Koordinatensystem. Bestimme die Nullstellen und den Schnittpunkt der Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Zeichne die Graphen
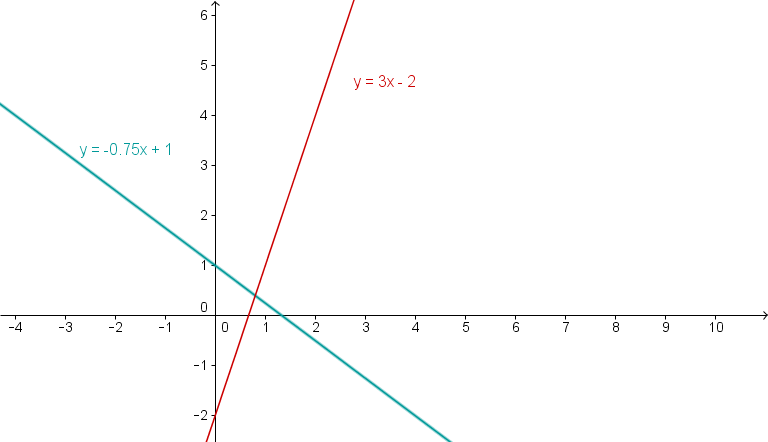
Bestimmung der Nullstellen
Setze y=0 um die Nullstelle zu bestimmen. Denn an der Stelle, an der y=0, schneidet die Gerade die x-Achse.
↓ Die erste Gerade hat bei eine Nullstelle.
Gehe für die zweite Gerade genauso vor.
↓ Setze y=0 um die Nullstelle zu bestimmen.
↓ Du dividierst durch einen Bruch Multipliziere mit dem Kehrwert
↓ Die zweite Gerade hat bei eine Nullstelle.
Bestimmung des Schnittpunkts
Setze die beiden Funktionsgleichungen gleich. Die Geraden schneiden sich dort, wo beide an der gleichen x-Stelle denselben y-Wert haben.
↓ Setze in eine der beiden Funktionen ein.
Der Schnittpunkt liegt bei .
- 13
Betrachte folgende Graphen.
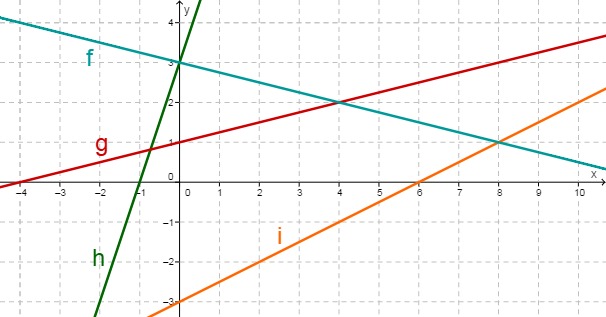
Bestimme die Funktionsgleichungen von allen 4 Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Um die Geradengleichung von f zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden f liegen. In diesem Fall ergibt sich zum Beispiel und . Bestimme mit diesen die Steigung von f mit der Formel.
Setz die Werte ein.
Bestimme jetzt den y-Achsenabschnitt , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf f liegt, oder abliest, bei welchem Wert f die y-Achse schneidet.
Setz zum Beispiel ein.
Vereinfache.
Also lautet die Geradengleichung .
Um die Geradengleichung von g zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden g liegen. In diesem Fall ergibt sich zum Beispiel und . Bestimme mit diesen die Steigung von g mit der Formel.
Setz die Werte ein.
Bestimme jetzt den y-Achsenabschnitt , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf g liegt, oder abliest, bei welchem Wert g die y-Achse schneidet.
Setz zum Beispiel ein.
Vereinfache.
Also lautet die Geradengleichung .
Um die Geradengleichung von h zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden h liegen. In diesem Fall ergibt sich zum Beispiel und . Bestimme mit diesen die Steigung von h mit der Formel.
Setz die Werte ein.
Bestimme jetzt den y-Achsenabschnitt , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf h liegt, oder abliest, bei welchem Wert h die y-Achse schneidet.
Setz zum Beispiel ein.
Vereinfache.
Also lautet die Geradengleichung .
Um die Geradengleichung von i zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden i liegen. In diesem Fall ergibt sich zum Beispiel und . Bestimme mit diesen die Steigung von i mit der Formel.
Setz die Werte ein.
Bestimme jetzt den y-Achsenabschnitt , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf i liegt, oder abliest, bei welchem Wert i die y-Achse schneidet.
Setz zum Beispiel ein.
Vereinfache.
Also lautet die Geradengleichung .
Hast du eine Frage oder Feedback?
Bestimme den Schnittpunkt von g und h , sowie die Nullstelle von f.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
Schnittpunkt von g und h
Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach um. Die Funktionsgleichungen lauten (Teilaufgabe a) und .
↓ Subtrahiere und 1.
↓ Dividiere durch .
Setz nun in die Geradengleichung von g oder h ein, um zu bestimmen.
Setz ein.
Die Geraden g und h schneiden sich also bei .
Die Nullstelle von f bestimmst du, indem du die Funktionsgleichung mit 0 gleichsetzt und nach umformst.
Die Nullstelle von f ist also 12.
Hast du eine Frage oder Feedback?
Berechne die beiden Schnittpunkte, die außerhalbdes Bildbereichs liegen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
Der Schnittpunkt von h und i und der Schnittpunkt von g und i liegen außerhalb des Bildbereichs.
Schnittpunkt von h und i
Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach um. Die Funktionsgleichungen lauten (Teilaufgabe a) und .
Setz nun in die Geradengleichung von h oder i ein, um zu bestimmen.
Setz ein.
Die Geraden h und i schneiden sich also bei .
Schnittpunkt von g und i
Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach um. Die Funktionsgleichungen lauten (Teilaufgabe a) und .
Setz nun in die Geradengleichung von g oder i ein, um zu bestimmen.
Setz ein.
Die Geraden g und i schneiden sich also bei .
Hast du eine Frage oder Feedback?
Wie viele Schnittpunkte gibt es höchstens bei vier Geraden, die jeweils nicht parallel sind?
Schnittpunkte kann es höchstens geben.Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Es gibt insgesamt 6 Schnittpunkte, nämlich die folgenden:
f und g
f und h
f und i
g und h
g und i
h und i
Hast du eine Frage oder Feedback?
- 14
Löse die folgenden Aufgaben.
Welche Steigung hat die Gerade durch die Punkte und ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: allgemeine Geradengleichung
Gegeben: Punkt und Punkt
Setze die x-Werte (erste Koordinate) und die y-Werte (zweite Koordinate) in die allgemeine Geradengleichung ein.
Bei der ersten Gleichung kannst du sofort ablesen, dass . Dieses kannst du in die zweite Gleichung einsetzen, um auszurechnen.
Setze und in die allgemeine Geradengleichung ein.
Hast du eine Frage oder Feedback?
Stelle die Gleichung der Geraden durch die Punkte und auf.
Gegeben: Punkt und
Berechne die Differenz der beiden x-Werte und der beiden y-Werte, um die Steigung zu bestimmen.
x-Werte:
y-Werte:
Während der x-Wert um steigt, nimmt der y-Wert um ab. Dividiere den y-Wert durch den x-Wert, um die Steigung auszurechnen.
Setze m, den x-Wert und den y-Wert eines der Punkte in die allgemeine Geradengleichung ein, um zu bestimmen.
Setze und in die allgemeine Geradengleichung ein, um die Gleichung der Funktion aufzustellen.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

