Aufgaben zu Bruchgleichungen
- 1
Löse folgende Bruchgleichung
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Der Nenner darf nie 0 werden! Daher muss ausgeschlossen werden.
Bei dieser Aufgabe musst du nur das auf die andere Seite bringen. Da im Nenner steht, musst du mit multiplizieren
Mit multiplizieren.
Durch 4 dividieren.
Da in der Definitionsmenge liegt, ist dies die Lösung der Bruchgleichung.
- 2
Bestimme jeweils die Lösungsmenge:
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Definitionsmenge bestimmen
Keiner der Nenner darf werden.
Aus der Definitionsmenge musst du alle Zahlen ausschließen, für die sich im Nenner ergeben würde.
Verboten ist hier also:
Daher müssen ausgeschlossen werden: und .
Die Definitionsmenge ist , wenn als Grundmenge die Menge der rationalen Zahlen verwendet wird.
Die Defintionsmenge ist , wenn als Grundmenge die Menge der reellen Zahlen verwendet wird.
Bruchgleichung lösen
Bilde den Hauptnenner. Der Hauptnenner ist bei dieser Gleichung: . Bringe nun alle Brüche durch Erweitern auf den Hauptnenner und multipliziere anschließend die gesamte Gleichung mit dem Hauptnenner, damit alle Brüche wegfallen.
↓ Bilde den Hauptnenner.
↓ Löse die Klammern auf,
und forme die Gleichung dann geeignet um.
Überprüfe nun noch, ob in der Definitionsmenge enthalten ist.
Damit ist Lösung der Gleichung und du kannst die Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Definitionsbereich bestimmen
Keiner der Nenner darf werden.
Aus der Definitionsmenge musst du alle Zahlen ausschließen, für die sich im Nenner ergeben würde.
Die Definitionsmenge ist , wenn als Grundmenge die Menge der rationalen Zahlen verwendet wird.
Die Defintionsmenge ist , wenn als Grundmenge die Menge der reellen Zahlen verwendet wird.
Lösungsmenge bestimmen
Bilde wieder den Hauptnenner der Brüche. Hier musst du den Faktor ausklammern im rechten Nenner.
↓ Bilde den Hauptnenner beider Brüche:
↓ Multipliziere nun mit dem Hauptnenner.
↓ Löse die Klammern auf.
Überprüfe nun noch, ob in der Definitionsmenge enthalten ist.
Damit ist Lösung der Gleichung, und du kannst die Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
- 3
Löse folgende Bruchgleichungen:
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
mit der Definitionsmenge .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Bruchgleichungen lösen
Es handelt sich hier um eine Bruchgleichung, also wende dein Wissen zur Lösung von Bruchgleichungen an.
Suche zunächst nach dem Hauptnenner. Dazu schaust du dir die Nenner an:
Diese kommen nur einmal vor und können nicht weiter faktorisiert werden. Den Hauptnenner erhälst du, wenn du die Bausteine zusammen multiplizierst.
↓ Erweitere beide Brüche auf den Hauptnenner
↓ Multipliziere die ganze Gleichung mit dem Hauptnenner
↓ ist in der Definitionsmenge enthalten, also ist die Lösungsmenge .
Hast du eine Frage oder Feedback?
Mit der Definitionsmenge .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Lösen der Bruchgleichung
Es handelt sich hier um eine Bruchgleichung, also wende dein Wissen zur Lösung von Bruchgleichungen an.
Ziel ist es die Gleichung Bruchtermfrei zu machen.Dazu benutzt du die Hauptnenner-Methode.
Hauptnenner finden
Suche zunächst nach dem Hauptnenner.
Dazu schaust du dir beide Terme der Gleichung an. Der Nenner von ist und der Nenner von ist .
Man bekommt die faktorisierten Bausteine:
Der Baustein kommt zweimal vor, für die Bildung des Hauptnenners braucht man es nur einmal. Alle anderen Bausteine kommen nur einmal vor.
Es ergibt sich für den Hauptnenner:
Brüche auf Hauptnenner erweitern
Zweiter Schritt der Hauptnenner-Methode ist es die Bruchterme so zu erweitern, dass der Hauptnenner im Nenner steht.
Gleichung bruchtermfrei machen
Nun kannst du mit dem Hauptnenner die Gleichung multiplizieren. So bekommst du eine bruchtermfreie Gleichung.
↓ Auf den Hauptnenner erweitern.
↓ mit dem Hauptnenner multiplizieren
Bruchtermfreie Gleichung lösen
Du hast die Bruchgleichung in eine äquivalente lineare Gleichung umgeformt. Diese kannst du nun mit deinem Vorwissen lösen.
ist in der Definitionsmenge enthalten, also ist die Lösungsmenge .
Hast du eine Frage oder Feedback?
mit der Definitionsmenge .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Bruchgleichungen
Es handelt sich hier um eine Bruchgleichung, also wende dein Wissen zur Lösung von Bruchgleichungen an.
Bringe zuerst beide Terme auf jeweils einen Bruch.
Die Gleichung lässt sich auf vereinfachen.
Beide Bruchterme haben als Nenner , also ist dieser auch der Hauptnenner.
↓ Auf den Hauptnenner erweitern und vereinfachen (siehe oben).
↓ Mit dem Hauptnenner multiplizieren.
ist in der Definitionsmenge enthalten, also ist .
Hast du eine Frage oder Feedback?
mit der Definitionsmenge .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Bruchgleichungen
Es handelt sich hier um eine Bruchgleichung, also wende dein Wissen zur Lösung von Bruchgleichungen an.
Bestimme zunächst den Hauptnenner. Schaue dir dafür explizit jeden Nenner einzeln an und faktorisiere falls möglich:
Aus den Faktoren ergibt sich für den Hauptnenner: .
Es folgt:
↓ Im . Bruch den Faktor und im . Bruch ausklammern.
↓ Auf den Hauptnenner erweitern.
↓ Vereinfache
↓ Mit dem Hauptnenner multiplizieren.
↓ Löse nach auf.
ist in der Definitionsmenge enthalten und somit eine Lösung der Gleichung. Also ist die Lösungsmenge
Hast du eine Frage oder Feedback?
- 4
Löse die folgende Bruchgleichung:
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Tipp: Hier kann dir der Artikel Bruchgleichungen lösen helfen. Wenn du dir noch unsicher bist, dann schau mal in den Kurs Bruchgleichungen rein.
Bruchgleichungen lösen
In dieser Lösung wirst du Wissen aus den Artikeln Über Kreuz multiplizieren und Buchgleichungen lösen brauchen.
Du möchtest diese Bruchgleichung lösen:
.
Definitionsmenge bestimmen
Zum Beginn musst du die Definitionsmenge der Bruchgleichung bestimmen. Diese kannst du bestimmen, indem du die Definitionslücken der Bruchgleichung bestimmst.
Wie du dich vielleicht erinnerst, entsteht eine Lücke genau bei der Zahl, wo einer der Nenner werden würde. Man darf nämlich nicht durch teilen.
Setzte nun die einzelnen Nenner nacheinander gleich :
Nenner des ersten Bruchs
Also wird dieser Nenner für
Der Nenner des zweiten Bruchs
Also wird dieser Nenner für
Der Nenner des dritten Bruchs
Diese Gleichung gilt, wenn entweder oder .
Also ist der Nenner des zweiten Bruchs genau dann gleich , wenn entweder oder .
Du erkennst also, dass hier und die Definitionslücken von der Bruchgleichung sind.
Insgesamt ist die Definitionsmenge der Bruchgleichung .
Gleichung bruchterm-frei machen
Der nächste Schritt ist die Gleichung von Brüchen zu befreien. Dies schafft man, indem man Über Kreuz multipliziert.
Der erste Schritt ist beide Seiten der Gleichung auf jeweils einen gleichen Nenner zu bringen:
Jetzt subtrahierst du die beiden Brüche auf der rechten Seite der Bruchgleichung voneinander:
Dann multplizierst du die Gleichung mit den beiden Nennern der Brüche:
und
Hier teilt man durch . Dies darf man, da nicht in der Definitionsmenge liegt.
Als letzter Schritt löst du nach x auf:
Also ist die Lösungsmenge der Bruchgleichung und die Definitionsmenge ist .
- 5
Gegeben ist die folgende Bruchgleichung:
Bestimme die Defintionsmenge und die Lösungsmenge!
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lösen von Bruchgleichungen
Bestimme die Definitionsmenge der Bruchgleichung
Zur Lösung der Bruchgleichung musst du zuerst die Defintionsmenge bestimmen. Dafür musst du die Nenner der einzelnen Brüche herausschreiben und gleich setzen. Da in jedem vorkommenden Bruch der Nenner ist, reicht es diesen Nenner gleich zu setzen.
Setze den Nenner gleich .
Du siehst jetzt, dass diese Gleichung bereits nach aufgelöst ist. Daher ist die Bruchgleichung nur für nicht definiert. Daher hat die Gleichung die Definitionslücke bei und du siehst:
Gleichung bruchterm-frei machen
Nun musst du die Gleichung bruchterm-frei machen. Dafür kannst du zunächst die Gleichung vereinfachen:
Multipliziere die Klammern aus.
Addiere auf beiden Seiten.
Vereinfache:
Alle vorkommenden Nenner sind gleich, nämlich . Der einzige Baustein ist , daher ist auch der Hauptnenner . Indem du jetzt die Gleichung mit diesem Hauptnenner multiplizierst, erhältst du eine bruchterm-freie Gleichung:
Multipliziere die Gleichung mit dem Hauptnenner .
Löse die bruchterm-freie Gleichung
Jetzt kannst du die lineare bruchterm-freie Gleichung lösen.
Addiere auf beiden Seiten der Gleichung .
Vereinfache den Term auf der linken Seite.
Dividiere beide Seiten der Gleichung durch .
Als Lösung der Gleichung erhältst du also .
Angabe der Lösungsmenge
Du musst jetzt noch überprüfen, ob die Lösung der Gleichung auch in der Definitionsmenge liegt. Wegen liegt in der Definitionsmenge und daher auch in der Lösungsmenge. Daher erhältst du: .
Die Lösungsmenge der Bruchgleichung ist also gegeben durch .
Versuche die Gleichung Bruchterm-frei zu machen. Dafür kannst du verschiedenen Methoden nutzen.
- 6
Bestimme die Definitions- und Lösungsmenge der Bruchgleichung:
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Bestimme zunächst die Definitionsmenge.Keiner der drei Nenner darf sein. Nicht erlaubt sind also:
Es müssen also die und die ausgeschlossen werden. Die Definitionsmenge der Gleichung ist somit .
Nun zur Lösungsmenge. Versuche zunächst die Bruchgleichung durch Über-Kreuz-Multiplizieren auf eine äquivalente bruchtermfreie Gleichung zu bringen. Danach kannst du die lineare Gleichung wie gewohnt lösen.
Klammere die aus, auf der rechten Seite der Bruchgleichung im ersten Nenner.
Kürze.
Addiere.
Ausmultiplizieren.
Subtrahiere x.
Dividiere durch 2.
Da in der Definitionsmenge enthalten ist, ist die Lösungsmenge .
- 7
Bestimme die Definitionsmenge und Lösungsmenge der Bruchgleichung:
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
Tipp: Für die bestimmung der Definitionsmenge musst du explizit die Nenner anschauen.
Versuche Überkreuz zu multiplizieren.
Die Idee ist die Bruchtermgleichung mit Hilfe von Äquivalenzumformungen in eine lineare Gleichung zu bringen. Dafür muss man zunächst die Definitionsmenge bestimmen und an geeigneter Stelle über Kreuz multiplizieren.
Bestimme also zunächst die Definitionmenge. Sowohl auf der linken Seite als auch auf der rechten Seite vom Gleichheitszeichen ist der Nenner der Terme .
Man darf also die nicht einsetzen.Für die Definitionsmenge gilt: .
Nun zur Lösungsmenge:
Versuche zunächst die Gleichung Bruchfrei zu machen.
Auf den gleichen Nenner bringen
Addiere
Überkreuzmultiplizieren
(Man darf durch teilen, weil nicht in der Definitionsmenge ist)
ist in der Definitionsmenge enthalten und somit eine Lösung der Gleichung.Es gibt keine weiteren Lösungen.
Also ist die Lösungsmenge der Gleichung .
- 8
Löse die Bruchgleichung.
Tipp: Versuche die Nenner zu faktorisieren und kürze die Brüche anschließend.
Definitionsmenge bestimmen
Kein Nenner darf werden, deshalb muss man bestimmte Werte ausschließen.
Es müssen die Zahlen und ausgeschlossen werden. Daher ist die Definitionsmenge
Bruchgleichung lösen
Für diese Bruchgleichung muss man den Hauptnenner finden. Es bietet sich aber an, zuerst alle Nenner zu faktorisieren.
↓ Die Nenner auf der linken Seite können nicht mehr faktorisiert werden, rechts allerdings schon.
↓ kürzen
↓ Nun kann man beim letzten Bruch das Minuszeichen vor dem Bruch mit dem Nenner verarbeiten, sodass sich dessen Summanden vertauschen.
Die Bausteine des Hauptnenners sind damit:
Mit dem Hauptnenner muss nun multipliziert werden und gleich gekürzt werden.
↓ Ausmultiplizieren
↓ Terme zusammenfassen
Da in der Definitionsmenge liegt, lautet die Lösungsmenge::
- 9
Bestimme die Definitionsmenge.
Hinweis zum Eingabefeld: Im Eingabefeld musst du nur die Zahl(en) eingeben, die nicht in der Definitionsmenge enthalten sind. Gib die Zahlen nur durch ein Leerzeichen getrennt ein (also kein Komma oder ähnliches), und ordne sie der Größe nach in aufsteigender Reihenfolge (das heißt, beginne mit der kleinsten).
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücke
Finde die Definitionslücken. Setze hierfür den Nenner des Bruchs gleich .
Du kannst erkennen, dass hier der Nenner wird, wenn ist.
Schließe die Definitionslücke aus der Definitionsmenge aus.
.
Die Definitionsmenge ist die Menge der rationalen Zahlen ohne die Zahl .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücke
Finde die Definitionslücken. Setze hierfür die Nenner beider Brüche gleich .
Du kannst erkennen, dass der Nenner wird für und .
Schließe die Definitionslücke aus der Definitionsmenge aus.
.
Die Definitionsmenge ist die Menge der rationalen Zahlen ohne die Zahl und die Zahl .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücke
Definitionsmenge
Für diese Aufgabe musst du wissen, was eine Definitionslücke ist und wie du die Definitionsmenge einer Bruchgleichung bestimmst.
Finde die Definitionslücken. Setzte den Nenner beider Brüche gleich .
1. Bruch:
2. Bruch:
Hier brauchst du einen Trick! Klammere aus und prüfe, wann einer der beiden Faktoren gleich wird.
Du musst jetzt prüfen, wann einer der beiden Faktoren wird. Setze sie jeweils gleich .
Du kannst erkennen, dass der Nenner des zweiten Bruchterms wird für und und der erste Bruchterm wird für .
Schließe die Definitionslücken aus der Definitionsmenge aus.
.
Die Definitionsmenge ist die Menge der rationalen Zahlen ohne die Zahlen , und .
Hast du eine Frage oder Feedback?
- 10
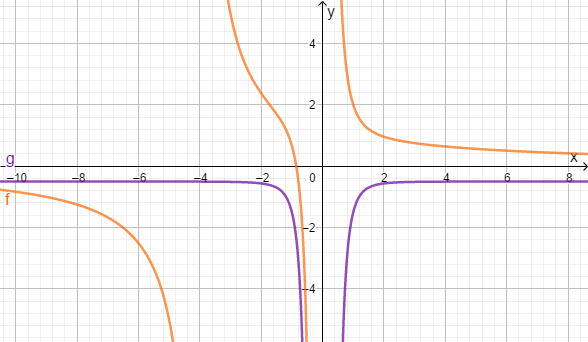
Welche Zahlen sind nicht in der Definitionsmenge der Bruchgleichung enthalten?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polstellen
Tipp: Suche die senkrechten Asymptoten!
Die Gleichung ist für bestimmte Zahlen nicht definiert. Sie werden Definitionslücken genannt. Diese müssen also aus der Definitionsmenge herausgenommen werden. Am Graphen erkennt man sie an der senkrechten Asymptote. In diesem Beispiel sind für beide Terme nicht definiert. Für ist definiert, aber nicht. Für die Definitionsmenge müssen alle diese Definitionslücken entfernt werden.
Hast du eine Frage oder Feedback?
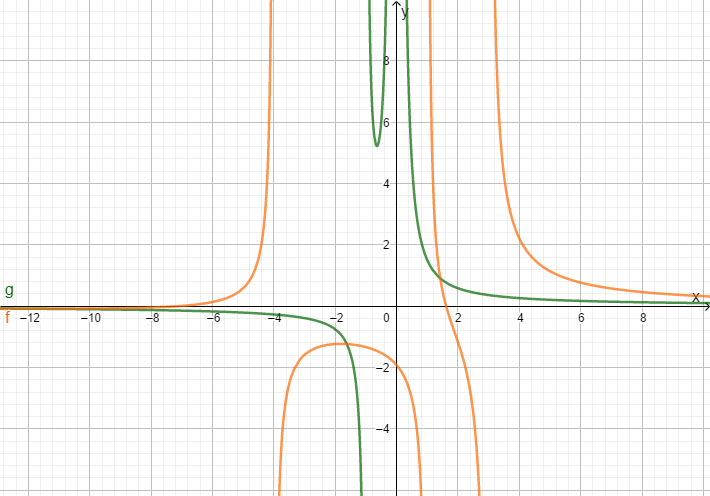
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polstellen
Tipp: Suche die senkrechten Asymptoten!
Die Gleichung ist für bestimmte Zahlen nicht definiert. Sie werden Defintionslücken genannt. Diese müssen also aus der Definitionsmenge rausgenommen werden. Am Graphen erkennt man sie an der senkrechten Asymptote. In diesem Beispiel erkennt man senkrechte Asymptoten bei . Diese müssen alle aus der Definitionsmenge rausgenommen werden.
Hast du eine Frage oder Feedback?
- 11
Warum muss man die Zahl aus der Definitionsmenge der folgendenen Gleichung ausschließen?
(Hinweis: Du musst die Lösungsmenge nicht bestimmen!)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücken
Bei Brüchen kann es Probleme mit der Definitionsmenge geben, wenn der Nenner des Bruches 0 wird. Setze deshalb in den Nenner auf der linken Seite ein:
Da der Nenner des Bruches wird, muss man die aus der Definitionsmenge ausschließen.
- 12
Gib die Lösungsmenge folgender Gleichungen an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Als erstes multiplizierst du mit , um das aus dem Nenner zu bekommen:
↓ ↓ vertausche die Seiten und kürze 12 und 6 mit 6 und dann 15 und 21 mit 3
Hast du eine Frage oder Feedback?
- 13
Beim Lösen einer Gleichung der Form muss man „Über-Kreuz-Multiplizieren“. Das heißt ist das Gleiche wie .
Wende dieses Vorgehen bei den folgenden Bruchgleichungen an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren
Definitionsmenge bestimmen
Zunächst musst du die Definitionsmenge der Gleichung bestimmen.
Keiner der beiden Nenner darf werden.
Deshalb musst du aus der Definitionsmenge alle Zahlen ausschließen, für die in einem der Nenner ergeben würde.
Verboten sind hier also:
Erste Gleichung lösen!
Zweite Gleichung lösen!
Daher müssen die Zahlen und aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.
Die Definitionsmenge ist , wenn als Grundmenge die Menge der rationalen Zahlen verwendet wird.
Bruchgleichung lösen
Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:
Über-Kreuz-Multiplizieren!
↓ ↓ Löse dann die Gleichung durch Umformen nach auf.
Überprüfe jetzt noch, ob in der Definitionsmenge enthalten ist. Es gilt , also ist die Lösungsmenge .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren
Definitionsbereich bestimmen
Zunächst musst du die Definitionsmenge der Gleichung bestimmen.
Keiner der beiden Nenner darf werden.
Aus der Definitionsmenge musst du deshalb alle Zahlen ausschließen, für die einer der Nenner ergeben würde.
Verboten sind hier also:
Löse die erste Gleichung!
Löse die zweite Gleichung!
Daher müssen die Zahlen und aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.
Die Definitionsmenge ist , wenn als Grundmenge die Menge der rationalen Zahlen verwendet wird.
Bruchgleichung lösen
Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:
↓ ↓ Löse nun die Gleichung nach auf!
Überprüfe jetzt noch, ob in der Definitionsmenge enthalten ist. also ist die Lösungsmenge .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren
Definitionsbereich bestimmen
Zunächst musst du die Definitionsmenge der Gleichung bestimmen.
Keiner der beiden Nenner darf werden.
Aus der Definitionsmenge musst du deshalb alle Zahlen ausschließen, für die einer der Nenner ergeben würde.
Verboten ist hier:
Löse die erste Gleichung.
Löse die zweite Gleichung.
Daher müssen die Zahlen und aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.
Die Definitionsmenge ist , wenn als Grundmenge die Menge der rationalen Zahlen verwendet wird.
Bruchgleichung lösen
Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:
Zunächst musst du die linke Seite der Gleichung auf einen gemeinsamen Bruch bringen.
↓ Den Summanden mit erweitern.
↓ Brüche auf der linken Seite addieren.
↓ Auf der linken Seite den Zähler zusammenfassen.
↓ Nun wendest du die Methode des Über-Kreuz-Multiplizierens an.
↓ ↓ Linke Seite zusammenfassen.
↓ Löse nach auf.
↓ Kürzen.
Überprüfe jetzt noch, ob in der Definitionsmenge enthalten ist. Wegen ist die Lösungsmenge .
Hast du eine Frage oder Feedback?
- 14
Löse die Bruchgleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Über Kreuz multiplizieren
Definitionsmenge bestimmen
Bei jeder Bruchgleichung muss man zu Beginn die Definitionsmenge bestimmen.
Kein Nenner darf werden.
Damit lautet die Definitionsmenge:
Bruchgleichung lösen
Bei dieser Bruchgleichung bietet sich das Verfahren Über Kreuz multiplizieren an.
↓ Ausmultiplizieren.
Da in der Definitionsmenge enthalten ist, lautet die Lösungsmenge:
- 15
Bestimme die Definitions- und Lösungsmenge der Bruchgleichung.
.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Tipp: Liegt deine Lösung wirklich in der Definitionsmenge?
Definitionsmenge bestimmen
Beide Nenner nehmen für den Wert an. Das darf nicht passieren. Deshalb muss man die aus der Definitionsmenge ausschließen.
Für die Definitionsmenge dieser Gleichung folgt:
.
Bruchgleichung lösen
Es bietet sich hier die Strategie "Über Kreuz multiplizieren" an. Hier sind beide Nenner sogar identisch.
.
.
Kürzen.
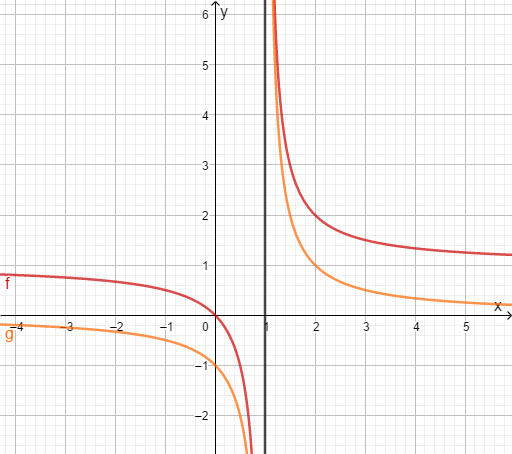
ist nicht in der Definitionsmenge enthalten und somit auch nicht in der Lösungsmenge.
Also ist keine Lösung der Gleichung.
An den zwei Graphen kann man erkennen, dass die Gleichung gar keine Lösung hat. Also gilt für die Lösungsmenge .
.
- 16
Handelt es sich um eine Bruchgleichung?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Eigenschaft

Durch bloßes Betrachten kannst du erkennen, dass in der Angabe eine Gleichung steht. Das Merkmal dafür ist das "".
Somit sind alle Bedingungen für eine Bruchgleichung vorhanden.
Die Antwort lautet: Ja, es ist eine Bruchgleichung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Folglich musst du die anderen Merkmale garnicht mehr prüfen.
Die Antwort lautet: Nein, es ist keine Bruchgleichung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Eigenschaft

Durch bloßes Betrachten kannst du erkennen, dass in der Angabe eine Gleichung steht. Das Merkmal dafür ist das "".
Somit sind alle Bedingungen für eine Bruchgleichung vorhanden.
Die Antwort lautet: Ja, es ist eine Bruchgleichung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Eigenschaft

Vorsicht! Keiner der Brüche hat eine Variable im Nenner.
Eine der Eigenschaften ist nicht erfüllt und somit handelt es sich nicht um eine Bruchgleichung.
Die Antwort lautet: Nein, es ist keine Bruchgleichung.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
Eigenschaft

Durch bloßes Betrachten kannst du erkennen, dass in der Angabe eine Gleichung steht. Das Merkmal dafür ist das "".
Eigenschaft und

Zudem sind Brüche, nämlich und , vorhanden. Diese haben ebenfalls eine Variable im Nenner.
Somit sind alle Bedingungen für eine Bruchgleichung vorhanden.
Die Antwort lautet: Ja, es ist eine Bruchgleichung.
Hast du eine Frage oder Feedback?
- 17
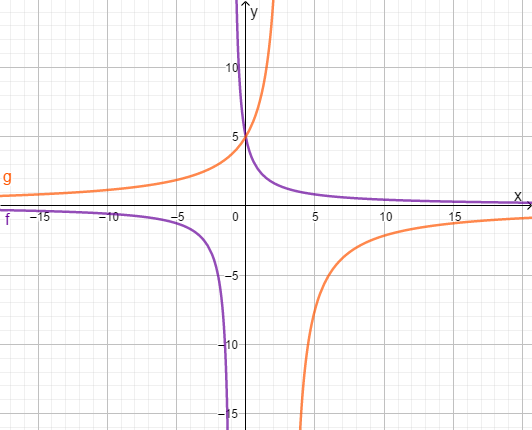
Bestimme die Lösungsmenge der Bruchgleichung mit Hilfe der Grafik!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte von Funktionen ablesen
Die Lösung der Gleichung ist die -Koordinate des Schnittpunkts!Die zwei Graphen haben genau einen gemeinsamen Schnittpunkt also gibt es genau eine Lösung! Dieser Schnittpunkt liegt bei . Also ist die Lösungsmenge .
Hast du eine Frage oder Feedback?
Die Lösungsmenge besteht aus den -Koordinaten aller Schnittpunkte
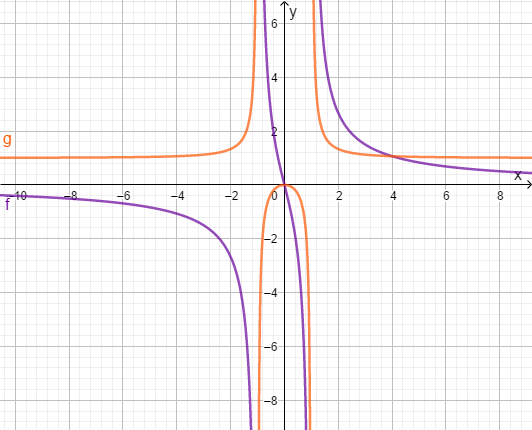
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte von Funktionen ablesen
Die Lösungsmenge besteht aus den -Koordinaten der Schnittpunkte der Graphen. Hier gibt es genau zwei Schnittpunkte, nämlich und . Also besteht die Lösungsmenge .
Hast du eine Frage oder Feedback?
Die Lösungsmenge besteht aus den -Koordinaten der Schnittpunkte!
- 18
Bestimme die Definitionsmenge und die Lösungsmenge von der folgenden Bruchgleichung:
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Defintionsmenge bestimmen
Als erstes musst du die Definitionsmenge bestimmen. Hierfür dürfen die Nenner der Bruchterme nicht 0 werden.
Damit ist die Definitionsmenge:
Bruchgleichung lösen
Hier bietet sich das Verfahren "Über Kreuz multiplizieren" an.
↓ Ausmultiplizieren
↓ Alles auf eine Seite bringen und somit 0 setzen.
↓ Mit der Mitternachtsformel lösen
↓ Beide Werte für ausrechnen
Da nicht in der Definitionsmenge enthalten ist, ist sie auch nicht Bestandteil der Lösungsmenge: .
Alternative Lösung
Suche den Hauptnenner und multipliziere beide Seiten der Gleichung damit.
Der Hauptnenner ist damit . Mit diesem werden beide Seiten multipliziert und die Brüche gekürzt.
↓ Ausrechnen
Da in der Definitionsmenge enthalten ist, lautet die Lösungsmenge:
- 19
Gib die Definitionsmenge an und bestimme eine äquivalente bruchtermfreie Gleichung von der folgenden Bruchgleichung:
(Du brauchst die bruchtermfreie Gleichung nicht zu lösen!)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Über Kreuz multiplizieren
Tipp: Es könnte helfen die linke Seite auf einen Nenner zu schreiben.
Um die Definitionsmenge zu bestimmen musst du alle Nenner gleich setzen.
Über Kreuz Multiplikation ist eine Äquivalenzumformung, wenn man die richtige Definitionsmenge betrachtet.
Bruchgleichungen
Die Aufgabe besteht aus zwei Teilen: Du sollst
die Definitionsmenge bestimmen, und
die Gleichung bruchtermfrei machen.
Definitionsmenge
Bestimme zunächst die Definitionsmenge der Bruchgleichung. Dazu schaust du dir die Nenner explizit an und schaust für welche Zahlen sie werden:
Für und ist die Gleichung nicht definiert. Also musst du sie aus der Definitionsmenge rausnehmen.
Die Definitionsmenge ist also: , falls die Grundmenge ist, und , falls die Grundmenge ist.
Umformen in bruchtermfreie Gleichung
Jetzt sollst du die Gleichung bruchtermfrei machen.
Du musst hier also zunächst die linke Seite zu einem Bruch umformen. Bringe auf einen Nenner.
Um eine Bruchgleichung bruchtermfrei zu machen kannst du zum Beispiel die Nenner über Kreuz multiplizieren.
Du kannst hier zunächst die linke Seite zu einem Bruch umformen. Bringe auf einen Nenner.
Addiere
Nun kannst du das Verfahren zum über Kreuz multiplizieren anwenden.
Diese Gleichung enthält keine Brüche. Da wir und aus der Definitionsmenge rausgenommen haben, haben wir insbesondere nicht mit der multipliziert.
Somit ist äquivalent zu .
Lösung der bruchtermfreien Gleichung
(in der Aufgabenstellung nicht gefordert)
linke Seite zusammenfassen
Alles auf eine Seite und somit 0 setzen.
Diskriminante berechnen.
Wegen D < 0 hat die quadratische Gleichung keine Lösungen und damit hat auch die Bruchgleichung keine Lösungen!
- 20
Zeichne die Graphen zu den Termen und in ein Koordinatensystem.
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Zeichnung
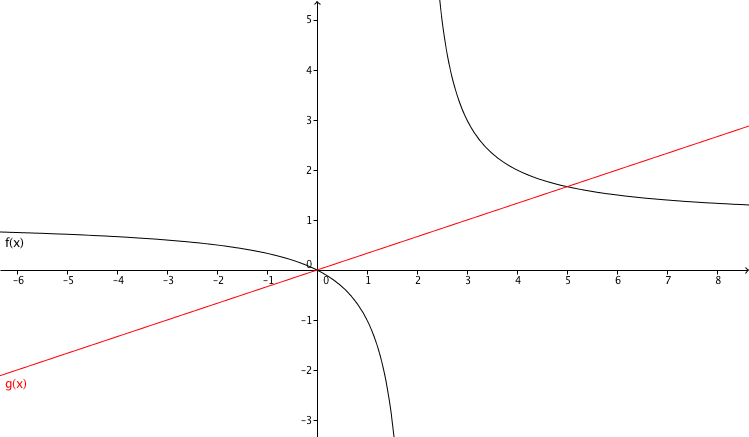
Bestimmung der Nullstelle
Ein Bruch wird Null, wenn der Zähler Null ist. Setze den Zähler gleich , also .
Der Graph hat bei eine Nullstelle.
Für nimmt den Wert an.
Bestimmung der Schnittpunkte
Ein Produkt wird 0, wenn einer der beiden Faktoren 0 ist.
Setze in eine der beiden Funktionen ein.
In der Definitionsmenge von muss nur ausgenommen werden, bei sind alle rationalen Zahlen erlaubt.
Daher ist die Lösungsmenge:
- 21
Gegeben ist der Graph einer linearen und einer gebrochenrationalen Funktion
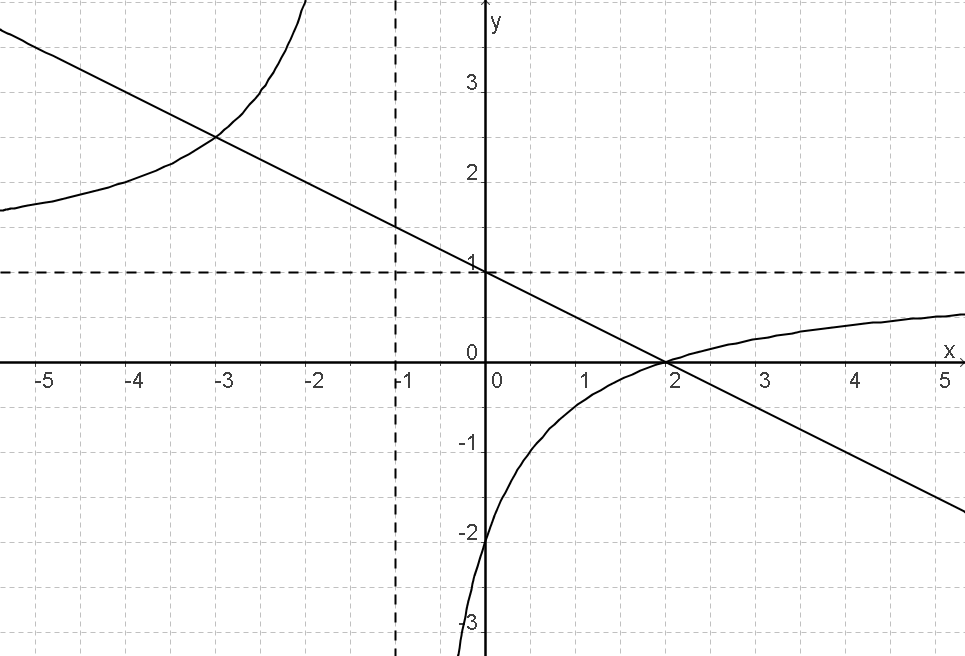
Die Zeichnung zeigt die Graphen der Funktionen mit den Funktionsgleichungen und .
Bestimme anhand der Zeichnung die Lösungsmenge der Gleichung .
Tipp: Gib deine Lösungen in aufsteigender Reihenfolge und durch ein Leerzeichen getrennt ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
Tipp: Gib deine Lösungen in aufsteigender Reihenfolge und durch ein Leerzeichen getrennt ein.
Schnittpunkte von Funktionen
Die Lösungsmenge der Gleichung repräsentiert die x-Werte, bei denen sich die Funktionen schneiden.
Hast du eine Frage oder Feedback?
Bestimme mit Hilfe des gegebenen Funktionsgraphen die Lösungsmenge der Gleichung .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
↓ An der Stelle, an der die gebrochenrationale Funktion den y-Wert hat, ist der x-Wert
Hast du eine Frage oder Feedback?
- 22
Zeichne die Graphen der Funktionen und
Lies die Koordinaten des Schnittpunkts der Graphen aus der Zeichnung ab und überprüfe dein Ergebnis rechnerisch. Trage dein Ergebnis gerne in das Eingabefeld unten in der Form ( | ), also z.B. (5|2), ein, bevor du dann in die Lösung schaust ;)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
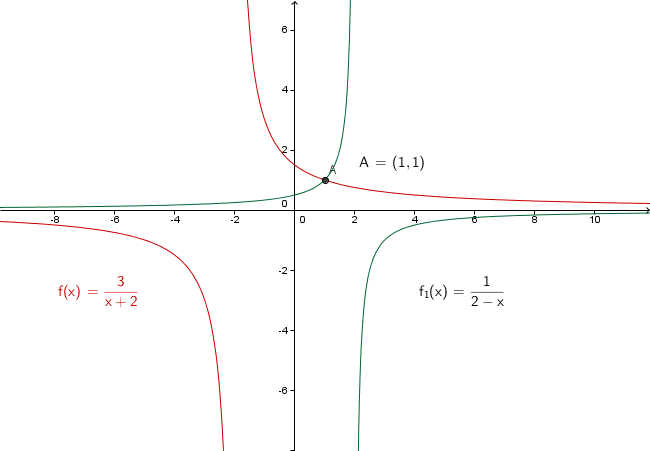
Der Schnittpunkt liegt bei .
Rechnung
Gleichsetzen der beiden Funktionsterme:
↓ ↓ ↓ Nach auflösen.
Einsetzen von in einen der Funktionsterme, z.B. in :
Also wurde auch rechnerisch gezeigt, dass der Schnittpunkt bei liegt.
- 23
Bestimme die Definitionsmenge und die Lösungsmenge von:
Tipp: Schaue dir jeden Bruch explizit an. Klammere aus und kürze, falls es möglich ist.
Achtung! Die Definitionsmenge bleibt gleich auch wenn die Nenner verschwinden.
Hier empfiehlt es sich zunächst mal die Brüche näher zu analysieren, Faktoren auszuklammern und eventuelle Kürzungen vorzuziehen:
Dies ergibt dann:
Gleicher Nenner
Auf beiden Seiten Kürzen
Wir bekommen also unendlich viele Lösungen. Um genau zu sein, ist hier die Lösungsmenge , die Definitionsmenge, also . Denn jedes ist für die Gleichung wohldefiniert und löst die gekürzte Gleichung, die unabhängig von ist.
Vorsicht Für die Zahlen , die wir aus der Definitionsmenge entfernt haben, ist die Gleichung weiterhin nicht definiert, obwohl sich der Nenner kürzen lässt.
- 24
Gegeben ist folgende Bruchgleichung:
Bestimme die Lösungsmenge!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomische Formel
Tipp: 3.Binomische Formel
Bruchgleichungen lösen
Um diese Aufgabe zu lösen, könnten dir die Artikel Binomische Formeln und Bruchgleichungen lösen helfen.
Du möchtest diese Bruchgleichung lösen:
Definitionsmenge bestimmen:
Um die Definitionsmenge bestimmen zu können, musst du sogenannte Definitionslücken der Bruchgleichung finden. Eine Lücke entsteht, sobald der Nenner eines Bruchs 0 wird. Man darf nämlich nicht durch 0 teilen.
Die Definitionsmenge ist also:
Der erste Nenner ist für x = -3, der zweite Nenner ist für x = -3 und x = 3 und der dritte Nenner ist für x = 3 nicht definiert. Daraus ergibt sich die Definitionsmenge.
Gleichung auflösen
Kürze die Brüche.
Löse den Bruch auf.
Löse die Klammer auf
und forme die Gleichung geeignet um!
Die Lösungsmenge ist somit
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
