Aufgaben zu Extremwerten

1
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
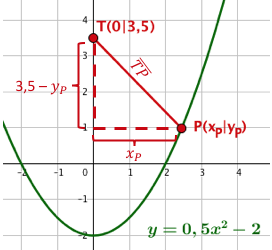
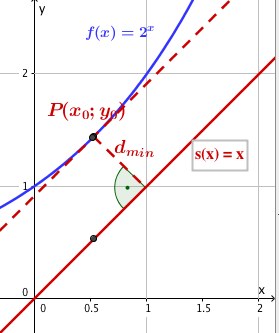
Welcher Punkt P auf der Parabel mit der Funktionsgleichung $\mathrm f(\mathrm x)=0{,}5\mathrm x^2-2$ hat vom Punkt $\mathrm T\left(0\;\left|\;3{,}5\right.\right)$ minimalen Abstand?
Wie groß ist dieser minimale Abstand?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Der Zeichnung entnimmst du die Zielfunktion und die Nebenbedingung dieser Extremwertaufgabe.
Zielfunktion:
Abstand der beiden Punkte $T$ und $P$ .
Nebenbedingung:
Der Punkt $P$ liegt auf der Parabel.
Gib die Zielfunktion an. Benutze dazu den Satz des Pythagoras.
Gib die Funktionsgleichung der Nebenbedingung an.
$\overline{TP}^2=x_P^2+(3{,}5-y_P)^2$
$\overline{TP}=\sqrt{x_P^2+(3{,}5-y_P)^2}$
Beachte: Für alle Punkte, für die der Abstand minimal wird, wird auch das Quadrat des Abstandes minimal.Deshalb nimmt man $\overline{TP}^2$ als Zielfunktion.
Dies erleichtert die Rechnung.
Zielfunktion:
$\overline{TP}^2=x_P^2+(3{,}5-y_P)^2$
Nebenbedingung:
$y_P=0{,}5x_P^2-2$
Setze die Nebenbedingung in die Zielfunktion ein.
$\overline{TP}^2(x_P)=x_P^2+(3{,}5-0{,}5x_P^2\color{red}{+}2)^2$
Fasse in der Klammer zusammen und quadriere mit der binomischen Formel.
$\overline{TP}^2(x_P)=0{,}25x_P^4-4{,}5x_P^2+30{,}25$
Bilde die Ableitung
$\overline{TP}^2(x_P)'=x_P^3-9x_P$
Setze die Ableitung gleich Null und löse die Gleichung.
$\def\arraystretch{1.25} \begin{array}{ccc}x_P^3-9x_P&=&0\\x_P(x_P^2-9)&=&0\\x_{P1}&=&0\\x_{P2}&=&+3\\x_{P3}&=&-3\end{array}$
Untersuche, für welche der Lösungen die 2. Ableitung positiv ist, damit jeweils ein Minmum vorliegt
$\def\arraystretch{1.25} \begin{array}{lcc}\overline{TP}^2(x_P)''&=&3 x_P^2- 9\\\overline{TP}^2(0)''&=&-9\\\overline{TP}^2(\pm3)''&=&+18\end{array}$
$x_P=0$ ergibt ein lokales Maximum des Abstandsquadrats.
$x_p=-3$ und $x_P=+3$ liefern ein Minimum des Quadrat des Abstandes und damit auch ein Minimum des Abstands.
Gib die drei Punkte und den dazu gehörigen Abstand an.
Einsetzen der drei $x_P$ -Werte in die Nebenbedingung:
$y(0)=-2$ $\quad\Rightarrow$ $P_0(0|-2)$ $\text {und}$ $\quad\overline{TP_0}=\sqrt{30{,}25}=5{,}5$
$y(\pm{3})=0{,}5\cdot9-2=2{,}5$ $\;\Rightarrow$ $\;P_{2|3}(\pm{3}|2{,}5)$ und $\overline{TP_{2/3}}=\sqrt{0{,}25\cdot81-4{,}5\cdot9+30{,}25}=\sqrt{10}\approx3{,}16$
Ergebnis:
Die beiden Punkte $P_1(-3|2{,}5)$ und $P_2(+3|2{,}5)$ haben von der Parabel mit rund $3{,}16\,\text{LE}$ den geringsten Abstand.
Im nachfolgenden Applet kannst du dies überprüfen indem du den Punkt $P$ verschiebst.
Alternative Lösung
Bei dieser Lösung ermittelst du in Frage kommende Parabelpunkt über eine Betrachtung von Tangenten der Parabel.
Für die drei Extremumspunkte $P_1$ , $P_2$ , $P_3$ gilt:
Die jeweilige Verbindungsstrecke zum Punkt $T$ steht senkrecht auf der Parabeltangente.
Parabel: $\quad\quad\quad\quad p(x)=0{,}5x^2-2$
Tangentensteigung: $\;p'(x)=x$
Gib die Steigung $m$ von $[TP]$ an.
$\displaystyle m_{[TP]}=\frac{y-3{,}5}{x}=\frac{0{,}5x^2-5{,}5}{x}\quad x\neq0$
Lotbedingung ansetzen!
$\def\arraystretch{2} \begin{array}{ccc} m_{[TP]}\cdot p'(x)&=&-1\;\;\;\;x\neq0\\ \\ \dfrac{0{,}5x^2-5{,}5}{x}\cdot{x}&=&-1\\ \\0{,}5x^2-5{,}5&=&-1\\x^2&=&9\\x_{2/3}&=&\pm3\end{array}$
Damit sind - auf anderem Weg - die x-Koordinaten der beiden Lösungspunkte der Extremumsaufgabe gefunden.
Zusatz:
Auch für den Punkt $P(0|-2)$ ("Maximumspunkt") steht die Tangente senkrecht auf der Verbindungsstrecke zu $T$ .
Bei dieser Aufgabe sollst du den minimalen Abstand eines Parabelpunktes von einem vorgegebenen Punkt "innerhalb" der Parabel als Extremwertaufgabe berechnen.

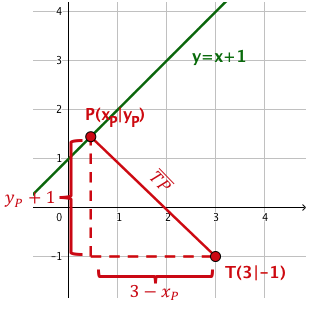
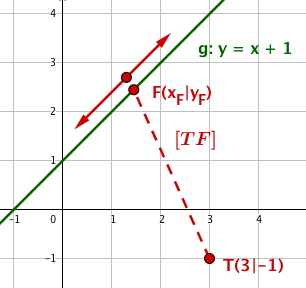
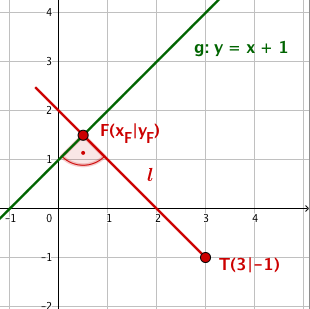
Welcher Punkt auf der Geraden g mit der Funktionsgleichung $\mathrm g(\mathrm x)=\mathrm x+1$ hat vom Punkt $\mathrm T\left(3\;\left|\;-1\right.\right)$ minimalen Abstand?

Wie groß ist dieser minimale Abstand?

Fertige zunächst eine Skizze an!

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe lösen

Abstand eines Punktes von einer Geraden

Bei dieser Aufgabe bestimmst du als Extremwertaufgabe denjenigen Punkt der Geraden, der von einem gegebenen Punkt außerhalb der Geraden den kleinsten Abstand hat.

Der Zeichnung entnimmst du die Zielfunktion und die Nebenbedingung dieser Extremwertaufgabe.

Darstellung und Analyse des Funktionsgraphen

Zielfunktion

Abstand der Punkte $P$ und $T$ .

Nebenbedingung

Der Punkt $P$ liegt auf der Geraden

$y=x+1$

Berechne die Zielfunktion mit Hilfe des Satzes des Pythagoras.

$\displaystyle \overline{TP}^2(x_P;y_P)$	$=$	$\displaystyle (3-x_P)^2+(y_P+1)^2$
	↓	Setze die Geradengleichung für y ein.
$\displaystyle \overline{TP}^2(x_p)$	$=$	$\displaystyle (3-x_p)^2+(x_p+2)^2$
	↓	Quadriere aus
$\displaystyle \overline{TP}^2(x_p)$	$=$	$\displaystyle 9-6x_p+x_p^2+x_p^2+4x_p+4$
	↓	Fasse zusammen
$\displaystyle \overline{TP}^2(x_p)$	$=$	$\displaystyle 2(x_p)^2-2x_p+13$	$\displaystyle \sqrt{}$
	↓	Ziehe die Wurzel
$\displaystyle \overline{TP}(x_P)$	$=$	$\displaystyle \sqrt{2(x_P)^2-2x_P+13}$

Beachte für Extremwertaufgaben mit einer Abstandsbedingung:

Für alle Punkte, für die der Abstand minimal oder maximal wird, ist auch das Quadrat des Abstandes minimal bzw. maximal, da gilt:

$0 < \overline{TP_1} < \overline{TP_2} \;\Leftrightarrow \;\overline{TP_1}^2 < \overline{TP_2}^2$ .

Da die Ableitung für $\overline{TP}^2$ bequemer zu berechnen ist, als für $\overline{TP}$ (keine Wurzel!), benutzt man als Zielfunktion ab hier das Quadrat des Abstandes.

$\displaystyle \overline{TP}^2(x_P)$	$=$	$\displaystyle 2(x_P)^2-2x_P+13$
	↓	Bilde die Ableitung
$\displaystyle \overline{TP}^2(x_P)'$	$=$	$\displaystyle 4x_P-2$
	↓	Setze die Ableitung gleich Null
$\displaystyle 0$	$=$	$\displaystyle 4x_P-2$	$\displaystyle +2$
$\displaystyle 2$	$=$	$\displaystyle 4x_P$	$\displaystyle :4$
$\displaystyle 0{,}5$	$=$	$\displaystyle x_p$

Berechne die 2. Ableitung der Zielfunktion, um dich zu versichern, dass $x_P=0{,}5$ ein Minimum des Quadrats des Abstandes liefert.

$\overline{TP}^2(x_P)''=+4>0$

$\Rightarrow x_P=0{,}5$

$\text{liefert Minimum}.$

Bestimme jetzt aus der Nebenbedingung $y_P$ :

$y_P=0{,}5+1=1{,}5$

$\Rightarrow$ $P(0{,}5|1{,}5)$ ist der gesuchte Punkt.

Berechne abschließend $\overline{TP}$ , nicht nur $\overline{TP}^2$ !!

Ergebnis:

Der minimale Abstand des Punktes $T(3|-1)$ von der Geraden $y=x+1$ beträgt:

$\overline{TP}\,\text{LE}=\sqrt{2\cdot 0{,}25-2\cdot 0{,}5+13}\,\text{LE}=\sqrt{12{,}5}\,\text{LE}\approx 3{,}54\,\text{LE}.$

Alternative Lösung

Ohne Kenntnisse aus der Differenzialrechnung kannst du die Aufgabe auch mit einer geometrischen Überlegung lösen:

Der gesuchte Punkt der Geraden $g$ mit kleinstem Abstand zum Punkt $T$ ist der Lotfußpunkt $F$ vom Punkt $T$ auf die Gerade $g$ .

Er kann

a) als Gleitpunkt auf der Geraden oder

b) als Schnittpunkt zweier Geraden

berechnet werden.

Fällung des Lots auf den Funktionsgraphen

a) Der Lotfußpunkt $F$ als Gleitpunkt auf $g$ .

Wenn die Strecke $[AF]$ auf der Geraden $g$ senkrecht stehen soll, muss für deren Steigungen $m_{[TF]}$ und $m_g$ gelten:

$\color{red}{m_{[TF]}\cdot m_g=-1}$ .

Also:

$\displaystyle \underbrace{\dfrac{y_F+1}{x_F-3}}_{\color{red}{=\;m_{[TF]}}}\cdot \underbrace{1}_{\color{red}{=\,m_g}}$	$=$	$\displaystyle -1$
	↓	Setze die Geradengleichung für y ein
$\displaystyle \dfrac{x_F+2}{x_F-3}$	$=$	$\displaystyle -1$	$\displaystyle \cdot (x_F - 3)$
$\displaystyle x_F + 2$	$=$	$\displaystyle -x_F + 3$	$\displaystyle + x_F -2$
$\displaystyle 2x_F$	$=$	$\displaystyle 1$	$\displaystyle :2$
$\displaystyle x_F$	$=$	$\displaystyle 0{,}5$

b) Der Lotfußpunkt $F$ liegt auf der Geraden $g$ , seine x-Koordinate hast du gerade berechnet, die y-Koordinate erhältst du durch einsetzen in $g$ :

$\displaystyle y$	$=$	$\displaystyle x+ 1$
$\displaystyle y$	$=$	$\displaystyle 0{,}5 + 1$
$\displaystyle y$	$=$	$\displaystyle 1{,}5$

Im nachfolgenden Applet kannst du die Rechnung überprüfen, indem du den Geradenpunkt $F$ verschiebst.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/pKD3xcuA]

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

3
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Der Absatz (Verkaufszahlen) einer Ware ist wesentlich abhängig vom Preis $p$ . Je höher der Preis, desto geringer ist in der Regel der Absatz.
Diesen Zuammenhang beschreibt die Preis-Absatz-Funktion (PAF)
Der Umsatz (Verkaufserlös) $U(p)$ ist als Produkt aus Absatz und Preis eine Wertgröße.
Eine Firma verkauft pro Monat von einem Artikel $n$ Stück zu einem Stückpreis von $p\,€$ .
Die Preis-Absatz-Funktion ist gegeben durch:
$PAF\;\;n(p)=1200-3\cdot p$
Bestimme den monatlichen Umsatz in Abhängigkeit vom Stückpreis p.
Für welchen Preis p ist der Umsatz maximal?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
In dieser Aufgabe aus dem Wirtschaftsleben sollst du den Zusammenhang zwischen Warenpreis und Verkaufserfolg, der am Umsatz gemessen wird, erfassen und den maximalen Umsatz als Extremwertaufgabe berechnen.
Anmerkung: Diese Lösungsskizze rechnet ohne Einheiten.
Gesucht: $U(p)$ und optimaler Preis
Stelle die Zielfunktion $U$ auf: monatlicher Umsatz = Stückzahl mal Preis.
$U(p)=n(p)\cdot p$
Erkenne die Nebenbedingung, die durch die Preis-Absatz-Funktion $PAF$ gegeben ist.
$PAF$ :
$n(p)=1200-3\cdot p\quad D_{PAF}=[0;400]$
Bestimme die Extremalfunktion $U(p)$ , also den monatlichen Umsatz in Abhängigkeit vom Preis, indem du in $U$ die Nebenbedingung einsetzt.
$U(p)=\left(1200\;-\;3\cdot p\right)\cdot p=1200p-3p^2$
Berechne die erste und zweite Ableitung.
Setze die erste Ableitung gleich Null und erkenne anhand der zweiten Ableitung, dass es sich um ein Maximum handelt.
Berechne $U_{max}$ .
$U_{max}=U(200)=(1200-3\cdot 200)\cdot 200=120\,000\,$
Ergebnis:
Der maximale monatliche Umsatz der Firma beim Verkauf des Artikels beträgt $120\,000\,€$ bei einem Stückpreis von $200\,€$ .

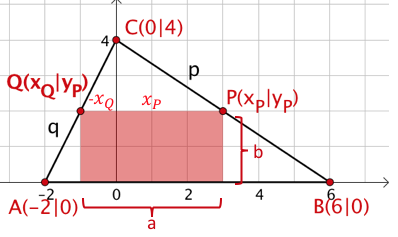
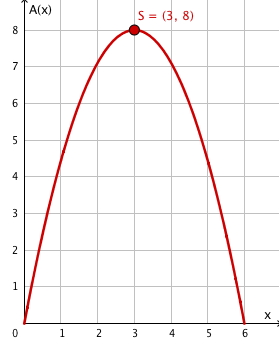
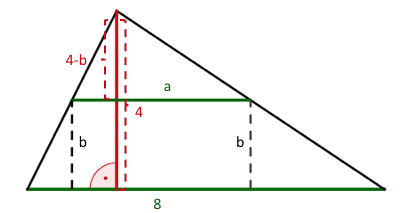
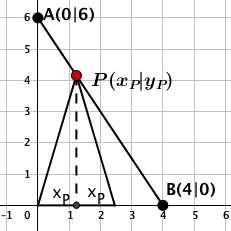
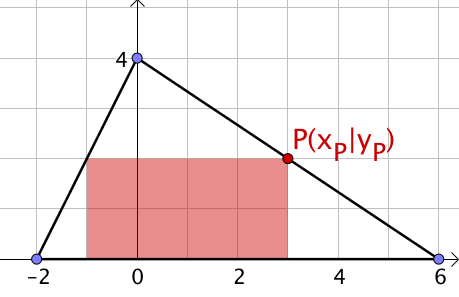
Dem abgebildeten Dreieck soll ein Rechteck mit möglichst großem Flächeninhalt einbeschrieben werden.

Berechne den größtmöglichen Flächeninhalt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

Bei dieser Aufgabe ist einem Dreieck ein größtmögliches Rechteck einzubeschreiben. Es handelt sich also um eine Extremwertaufgabe

Wenn du eine Rechtecksseite auf die Grundlinie des Dreiecks legst, bedeutet die Forderung des "Einbeschreibens", dass die beiden weiteren Rechteckspunkte $P$ und $Q$ jeweils auf den anderen Seiten des Dreiecks liegen. Dies ergibt zwei Nebenbedingungen für die Extremwertaufgabe.

Da der Flächeninhalt maximiert werden soll, benötigst du zunächst als Zielfunktion die Formel für den Flächeninhalt eines Rechtecks, in die du dann die Nebenbedingungen "einarbeiten" musst.

Zielfunktion

$A(a;b)=a\cdot b$ mit $a=x_P\color{red}{-}x_Q\;(\text{da}\,x_Q<0)$ und $b=y_P$ also:

$A(x_P;y_P;x_Q)=(x_P-x_Q)\cdot y_P$

1. Nebenbedingung

$P(x_P|y_P)$ liegt auf der Geraden $p$ .

Stelle die Gleichung der Geraden $p$ mit Hilfe der Punkte $B\left(6|0\right)$ und $C\left(0|4\right)$ auf.

$\displaystyle m_P=\frac{4-0}{0-6}=-\frac23$

$t=4$

$\Rightarrow\,(1)\;p:\,y_P=-\dfrac23\cdot x_P+4$

Gib nun die 2. Nebenbedingung an.

2. Nebenbedingung

$Q(x_Q|\color{red}{y_P})$ liegt auf der Geraden $q$ .

Stelle die Gleichung der Geraden $q$ mit Hilfe der Punkte $A\left(-2|0\right)$ und $C\left(0|4\right)$ auf.

$\displaystyle m_Q=\frac{4-0}{0+2}=+2$

$t=4$

$\Rightarrow\;(2)\;q:\,y_P=2\cdot x_Q+4$

Löse nach $x_Q$ auf.

$\displaystyle y_p$	$=$	$\displaystyle 2\cdot x_Q+4$	$\displaystyle -4$
$\displaystyle y_p - 4$	$=$	$\displaystyle 2\cdot x_Q$	$\displaystyle :2$
$\displaystyle 0{,}5y_P - 2$	$=$	$\displaystyle x_Q$
	↓	Setze für $y_P$ den Term aus (1) ein.
$\displaystyle 0{,}5(-\dfrac23 x_P+4)-2$	$=$	$\displaystyle x_Q$
	↓	Multipliziere die Klammer aus
$\displaystyle -\dfrac13 x_P$	$=$	$\displaystyle x_Q$

Setze $y_P=-\dfrac23 \cdot x_P+4$ und $x_Q=-\dfrac13 \cdot x_P$ in die Zielfunktion $A(x_P;y_P;x_Q)=(x_P-x_Q)\cdot y_P$ ein, um die Zielfunktion in Abhängigkeit der einzigen Variablen $x_P$ zu erhalten.

$\displaystyle A(x_P)$	$=$	$\displaystyle (x_P+\dfrac13 x_P)\cdot (-\dfrac23 x_P+4)$
	$=$	$\displaystyle \dfrac43x_P\cdot (-\dfrac23x_P + 4)$
	↓	Multipliziere aus
	$=$	$\displaystyle -\dfrac89x_P^2+\dfrac{16}{3}x_P$

$\mathbb{D}=]0;6[$

Bilde die Ableitung $A'(x_P)$ .

$\displaystyle A'(x_P)=-\frac{16}{9}x_P+\frac{16}{3}$

Setze $A'(x_P)$ gleich Null und löse die Gleichung.

$\displaystyle 0$	$=$	$\displaystyle -\dfrac{16}{9}x_P+\dfrac{16}{3}$	$\displaystyle + \dfrac{16}{9}x_P$
$\displaystyle \dfrac{16}{9}x_P$	$=$	$\displaystyle \dfrac{16}{3}$	$\displaystyle :\dfrac{16}{9}$
$\displaystyle x_P$	$=$	$\displaystyle 3$

Überprüfe mit der 2. Ableitung, ob sich für $x_P=3$ tatsächlich ein Maximum ergibt.

$A''(x)=-\dfrac{16}{9}$

$A''(x)$ ist eine konstante Funktion. Somit ist auch $A''(3)<0$ und $x_P=3$ ergibt eine größtmögliche Rechtecksfläche.

Setze $x_P=3$ in die Fläche $A(x_P)$ ein.

Flächeninhalt:

$\displaystyle A(x_P)=-\frac89\cdot x_P^2 +\frac{16}{3}\cdot x_P$

$\Rightarrow$

$\displaystyle A(3)=-\frac89 \cdot 9+\frac{16}{3} \cdot 3=8$

Setze $x_P=3$ auch noch in die 1. Nebenbedingung ein, um die 2. Koordinate des Eckpunktes P zu erhalten.

Nebenbedingung:

$\displaystyle y_P=-\frac23 \cdot x_P+4$

$\Rightarrow\quad y_P=-\dfrac23 \cdot 3+4=2$

Ergebnis:

Mit dem Eckpunkt $P(3|2)$ ist das größtmögliche Rechteck in das Dreieck einbeschrieben und hat den Flächeninhalt $8\,\text{LE}^2$ .

Alternative Lösung 1

Der Graph der Zielfunktion $\displaystyle A(x)=-\frac89 x^2+\frac{16}{3}x,\quad\mathbb{D}=]0;6[$

ist eine nach unten geöffnete Parabel.

Ihr Maximum ist der Scheitelpunkt. Diesen kann man - außer über die Ableitung von $A(x)$ - durch eine quadratische Ergänzung ermitteln.

$\displaystyle A(x)$	$=$	$\displaystyle -\dfrac89x^2+\dfrac{16}{3}x$
	↓	Klammere $\displaystyle -\frac89$ aus.
	$=$	$\displaystyle -\dfrac89 (x^2-6x)$
	↓	quadratisch ergänzen
	$=$	$\displaystyle -\dfrac89 (x^2-6x \color{red}{+3^2})\color{red}{+8}$
	↓	2. binomische Formel benutzen.
$\displaystyle A(x)$	$=$	$\displaystyle -\dfrac89 (x-3)^2+8$

Lies den Scheitelpunkt ab $\Rightarrow S(3|8)$

Dessen 2. Koordinate liefert den gesuchten maximalen Flächeninhalt eines dem Dreieck einbeschriebenen Rechtecks.

$A_{max}=8\;\text{LE}^2$

Im nachfolgenden Applet kannst du durch Verschieben des Punktes P das Ergebnis kontrollieren.

[https://www.geogebra.org/material/iframe/id/yvjtyqar]

Alternative Lösung 2

Die gestellte Aufgabe lässt eine verblüffend einfache Lösung zu. Dabei wird das Koordinatensystem nicht benötigt, sondern sie ergibt sich aus dem Strahlensatz.

Entscheidend für diese Möglichkeit ist, dass vom Dreieck $ABC$ neben der Grundlinie $\overline{AB}=8\,\text{LE}$ die Höhe auf diese Seite mit $h=y(C)=4\,\text{LE}$ gegeben ist.

Zielfunktion ist die Formel für die Fläche des Rechtecks mit den Seitenlängen $a\,LE$ und $b\,LE$ . Also:

$A(a;b)=a\cdot b$

Die Nebenbedingung ergibt sich aus dem Strahlensatz.

Benutze den Strahlensatz und erhalte:

$\displaystyle \dfrac{a}{8}$	$=$	$\displaystyle \dfrac{4-b}{4}$	$\displaystyle \cdot 4$
$\displaystyle 0{,}5a$	$=$	$\displaystyle 4-b$	$\displaystyle + b - 0{,}5a$
$\displaystyle b$	$=$	$\displaystyle 0{,}5a + 4$

Setze $b$ in $A(a;b)$ ein.

$A(a)=a\cdot (-\dfrac 12 a+4)$

$A(a)=-\dfrac 12 a^2+4a$

Die Zielfunktion $A(a)$ ist eine nach unten geöffnete Parabel. Deshalb ergibt die y-Koordinate des Scheitelpunktes den maximal möglichen Flächeninhalt einbeschriebener Rechtecke.

Den Scheitelpunkt berechnest du über die Ableitung von $A(a)$ oder mit einer quadratischen Ergänzung.

Ableitung von $A(a)$

$A'(a)=-a+4$

$A'(a)=0\,\Rightarrow\,a=4$

$\Rightarrow\,A_{max}=8$

quadratische Ergänzung

$A(a)=-\frac{1}{2}(a^2-8a\color{red}{+4^2})\color{red}{+8}$

$=-\frac 12(a-4)^2+8$

$\Rightarrow\,S(4|8)$

Vertiefung der Aufgabe

In der gegebenen Aufgabenstellung soll das Rechteck dem Dreieck $ABC$ so einbeschrieben werden, dass eine Rechteckseite auf der Grundseite $[AB]$ liegt.

Natürlich kann man Rechtecke auch so einbeschreiben, dass eine Rechteckseite auf einer der beiden anderen Dreieckseiten liegt.

Dann stellt sich die Frage: Haben die maximal möglichen Flächeninhalte auch bei den beiden anderen Lagen den gleichen Wert?

Dass dies tatächlich so ist, kannst du am folgenden Applet nachvollziehen, indem du die unterschiedlichen Gleitpunkte $P_1$ , $P_2$ oder $P_3$ verschiebst.

[https://www.geogebra.org/material/iframe/id/XVmPdA8N]

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Die Gemeinde Haar weist neues Bauland aus.

Herr Meier hat die dreieckige Fläche gekauft, muss aber nun (wie vorgeschrieben) ein rechteckiges Baugrundstück festlegen.

Wie sollte sich Herr Meier entscheiden, wenn er ein möglichst großes Baugrundstück haben will?

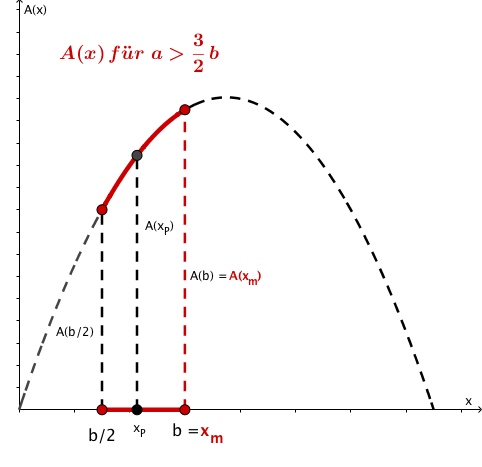
Ein Punkt $P(x_P|y_P)$ gleite auf der Strecke $[AB]$ mit $A(0|6)$ und $B(4|0)$ .

Er ist die Spitze eines gleichschenkligen Dreiecks mit einer festen Ecke im Koordinatenursprung.

Für welchen Punkt $P$ hat das Dreieck den größtmöglichen Flächeninhalt? Wie groß ist dieser?

Im nachfolgenden Applet kannst du - bevor du rechnest - experimentieren.

[https://www.geogebra.org/material/iframe/id/guvv2try]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben

Für das gleichschenklige Dreieck mit der Spitze $P$ gilt:

Grundlinie = $2\cdot x_P$

Höhe = $y_P$

Für die Dreiecksfläche ergibt sich also:

$A_{Dreieck}=x_P\cdot y_P$

Skizze der Situation im Koordinatensystem

Gib die Zielfunktion und die Nebenbedingung für die Extremumsaufagbe an.

Zielfunktion

$\displaystyle A_{Dreieck}=x_P\cdot y_P$

Nebenbedingung

Der Punkt $P(x_P|y_P)$ liegt auf der Strecke $[AB]$ .

Ermittle die Geradengleichung $AB$ .

allgemeiner Ansatz einer Geradengleichung:

$\mathrm g(\mathrm x)=\mathrm{mx}+\mathrm t$

Bestimme den y-Achsenabschnitt $t$ , indem du abliest, wo der Graph die y-Achse schneidet.

$\Rightarrow\;\;\mathrm t=6$

Bestimme die Steigung m, indem du ein Steigungsdreieck benutzt:

Gehe von irgendeinem Geradenpunkt $1\,LE$ nach rechts und lies ab, wie viele Einheiten du nach unten gehen musst, um wieder auf den Funktionsgraphen zu treffen.

$\Rightarrow\;\;\mathrm m=-1{,}5$

Setze die Werte $m$ und $t$ in die Funktionsgleichung ein.

$\Rightarrow\;\;\mathrm g(\mathrm x)=-1{,}5\mathrm x+6$

Gib noch den Definitionsbereich $D_g$ an, mit dem die Gerade $g$ auf die Strecke $[AB]$ begrenzt wird.

$D_g=[0;4]$

Gib nun die Nebenbedingung als Funktionsgleichung für den Punkt $P(x_P|y_P)$ an.

Nebenbedingung

$y_P=-1{,}5\cdot x_P+6$

Zielfunktion

$A(x_P;y_P)=x_P\cdot y_P$

Setze $y_P$ der Nebenbedingung in die Zielfunktion ein.

$A(x_P)=-1{,}5\cdot x_P^2+6\cdot x_P$

Es handelt sich um eine nach unten geöffnete Parabel.

Ihr Maximum lässt sich über die Scheitelform durch eine quadratische Ergänzung ermitteln.

$\def\arraystretch{1.25} \begin{array}{rcl}A(x_P)&=&-1{,}5(x_P^2\color{red}{-4}x_P)\\&=&-1{,}5(x_P^2-4x_P\color{red}{+2^2})\color{red}{+6}\\&=&-1{,}5(x_P-2)^2+6\end{array}$

Lies den Scheitelpunkt ab.

$\Rightarrow\;\;\mathrm S\left(2\;\left|\;6\right.\right)$

Gib die Bedeutung der Koordinaten des Scheitelpunktes an.

$\Rightarrow\;$ Bei ${\mathrm x}_\mathrm p=2$ ist der Flächeninhalt $6\,\text{LE}$ und dies ist der gesuchte größtmögliche Flächeninhalt des gleichschenkligen Dreiecks.

Bestimme aus der Nebenbedingung den y-Wert des Punktes $P$ .

${\mathrm y}_\mathrm p=-1{,}5\cdot2+6=3$

Gib den gesuchten Punkt $P$ und den maximalen Flächeninhalt in einem Antwortsatz an.

Für den Punkt $\mathrm P\left(\left.2\;\right|\;3\right)$ ist der Flächeninhalt des darunterliegenden Dreiecks maximal und er beträgt $6\;\mathrm{FE}$ .

Weitere Lösungsmöglichkeit über die Ableitung von $A(x_P)$

$\def\arraystretch{1.25} \begin{array}{rcl}A(x_P)&=&-1{,}5x_P^2+6x_P\\A'(x_P)&=&-3x_P+6\end{array}$

Setze $A'(x_P)$ gleich Null und löse nach $x_P$ auf.

$\displaystyle A'\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle -3x_P+6$	$=$	$\displaystyle 0$	$\displaystyle +3x_P$
$\displaystyle 6$	$=$	$\displaystyle 3x_P$	$\displaystyle :3$
$\displaystyle 2$	$=$	$\displaystyle x_P$

Setze den Wert in $A(x_P)$ und in die Nebenbedingung $y=-1{,}5\cdot x_P+6$ ein und du hast die Lösung der Aufgabe.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

7
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Auf einem Bauernhof möchte der Bauer eine rechteckige Koppel für seine Pferde anlegen.
Die Koppel liegt an einem Fluss und soll deshalb nur an drei Seiten eingezäunt werden.
Der zur Verfügung stehende Zaun ist 120m lang.
Wie muss der Bauer die Koppel anlegen, damit sie eine möglichst große Weidefläche hat?
Wie groß ist die Weidefläche dieser Koppel?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe zur Berechnung einer maximalen Weidefläche
Gegeben: kombinierte Länge von drei Seiten
Gesucht: ideale Seitenlänge für maximale Fläche
$A=l\cdot b$
Bestimme die Zielfunktion, nämlich die Fläche eines Rechtecks mit den Seitenlängen $a$ und $b$
$2\cdot b+l=120$
Stelle die Nebenbedingung auf. Da man für eine Seite (z. B. l) keinen Zaun benötigt, verändert sich die Nebenbedingung im Vergleich zur normalen Umfangsformel $U=2\left(l+b\right)$ etwas.
$A(b)=(120-2b)\cdot b=120b-2b^2$
mit $b>0$
Setze die Nebenbedingung in die Zielfunktion ein und erhalte die Extremalfunktion. Beachte dabei, dass b sinnvollerweise nur positive Werte annehmen kann.
$A'(b)=120-4b$
$A''(b)=-4$
Leite die Extremalfunktion zweimal ab, um im nächsten Schritt den Extremwert und die Art des Extremwertes bestimmen zu können.
$A'=120-4b=0$
$120=4b$
$b=30$
Setze die erste Ableitung gleich Null und setze die Lösung dieser Gleichung in die zweite Ableitung ein. Du erkennst dann, dass der Extremwert tatsächlich wie gewünscht ein Maximum ist.
$l=120-2\cdot30=60$
$A=60\cdot30=1800$
Berechne nun noch $l$ durch Einsetzen der Breite $b$ in die Nebenbedingung und die Fläche der Weidekoppel.
Für die maximale Weidefläche muss der Bauer die Koppel also 60 m lang und 30 m breit wählen. Damit erreicht er eine Weidefläche von 1800 m².

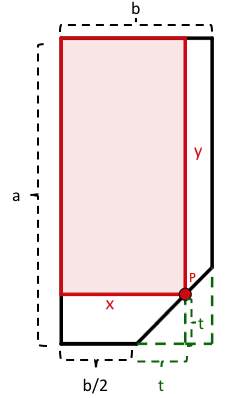
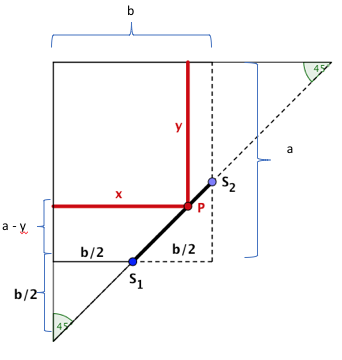
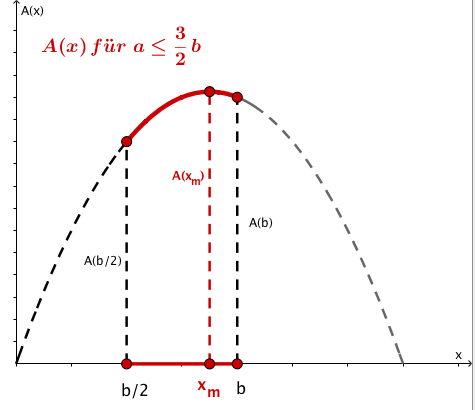
Aus einer rechteckigen Fensterscheibe mit den Seitenlängen $a\,LE$ und $b\,LE$ , ist vom unteren Mittelpunkt der kleineren Seite $b$ aus, eine Ecke geradlinig unter einem Winkel von 45° abgesprungen.

Aus der restlichen Scheibe soll durch Schnitte parallel zu den ursprünglichen Seiten eine möglichst große rechteckige Scheibe hergestellt werden.

Welche Seitenlängen und welche Fläche hat die "Ersatzscheibe"? In welchem Punkt setzen die Schnitte an?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben

Bei dieser Aufgabe soll ein größtmöglicher Flächeninhalt bestimmt werden. Es handelt sich also um eine Extremwertaufgabe.

Die Scheibe sei höher als breit. Also gelte: $a>b$ .

Das abgeschnittene Stück der Scheibe ist wegen des Neigungswinkels von 45° ein gleichschenklig-rechtwinkliges Dreieck mit der Kathetenlänge von $b/2\,LE$ .

Die gesuchte rechteckige "Ersatzscheibe" habe die Seitenlängen $x\,LE$ und $y\,LE$ und entsteht von einem Punkt $P$ aus, der auf der abgebrochenen Schnittkante variiert.

Die Zielfunktion ist der Flächeninhalt $A(x;y)$ eines Rechtecks mit den Seiten $x\,LE$ und $y\,LE$ :

$A(x;y)=x\cdot y$ ,

wobei

$\dfrac{b}{2}\le x\le b$ und $a-\dfrac{b}{2}\leq y \leq a$

Grafische Veranschaulichung

Die Nebenbedingungen für $P$ ergeben sich aus dessen variabler Lage auf der Schnittkante und können mit einem variablen Parameter $t$ so angegeben werden:

$x=\dfrac{b}{2}+t$ $\quad\text{und}$

$y=a-t$ $\quad\text{wobei}\;\text{gilt}$

$0 \leq t\leq \dfrac{b}{2}$

Setze die Nebenbedingungen in die Zielfunktion ein, um diese als Funktion der Variablen $t$ zu erhalten.

Zielfunktion

$\displaystyle A\left(t\right)$	$=$	$\displaystyle \left(\dfrac{b}{2}+t\right)\cdot\left(a-t\right)$
	↓	Bilde - z.B. mit der Produktregel - die 1. Ableitung $A'(t)$ und die 2. Ableitung $A''(t)$ .
$\displaystyle \mathbb{D}_{A(t)}=[0;b/2]$	$=$	$\displaystyle \left[0;\dfrac{b}{2}\right]$
$\displaystyle A´\left(t\right)$	$=$	$\displaystyle -2t+a-\dfrac{b}{2}$
	↓	Setze $A'(t)$ gleich Null und löse die Gleichung.
$\displaystyle A´´\left(t\right)$	$=$	$\displaystyle -2$
$\displaystyle A´´\left(t\right)$	$<$	$\displaystyle 0$
$\displaystyle -2t+a-\dfrac{b}{2}$	$=$	$\displaystyle 0$
$\displaystyle t$	$=$	$\displaystyle \dfrac{a}{2}-\dfrac{b}{4}$

Zwischenstand der Lösung:

Die gesuchte Ersatzscheibe mit maximalem Flächeninhalt wird von einem variablen Punkt P aus erzeugt, der auf der Strecke $[S_1;S_2]$ liegen muss.

Damit ist der Definitionsbereich der Flächen-Zielfunktion $A(t)$ auf das Intervall $[0;\dfrac{b}{2}]$ begrenzt.

$A(t)$ ist wegen $A''(t)<0$ eine nach unten geöffnete Parabel und der errechnete Wert $t_{max}=\dfrac{a}{2}-\dfrac{b}{4}$ liefert ein lokales Maximum - also einen maximalen Flächeninhalt, aber nur dann, wenn der Wert im Intervall $[0;\dfrac{b}{2}]$ liegt.

Da $a>b$ ist jedenfalls $t_{max}>0$ .

$t_{max}$ ist aber nicht für jedes Zahlenpaar $a$ und $b$ kleiner als $\dfrac{b}{2}$ , da gilt:

$\displaystyle \dfrac{a}{2}-\dfrac{b}{4}$	$≤$	$\displaystyle \dfrac{b}{2}$
$\displaystyle \dfrac{a}{2}$	$≤$	$\displaystyle \dfrac{3}{4}b$
$\displaystyle a$	$≤$	$\displaystyle \dfrac{3}{2}b$

Fallunterscheidung:

Fall 1: $\quad b<a\leq \dfrac{3}{2}b\quad$ ("a nicht zu groß") $\Rightarrow\;t_{max}\in [0;\dfrac{b}{2}]$

Fall 2: $\,\quad a>\dfrac{b}{2}\quad \;\, \quad\quad$ ("a beliebig groß") $\Rightarrow\;t_{max}\notin[0;\dfrac{b}{2}]$

Setze $t_{max}$ in $A(t)$ ein.

Fall 1:

$\;b<a\leq \dfrac{3}{2}b$

$t_{max}$ liefert lokales Maximum

$\displaystyle A\left(t_{\max_{ }}\right)$	$=$	$\displaystyle \left(\dfrac{b}{2}+\dfrac{a}{2}-\dfrac{b}{4}\right)\cdot\left(a-\dfrac{a}{2}+\dfrac{b}{4}\right)$
	$=$	$\displaystyle \left(\dfrac{b}{4}+\dfrac{a}{2}\right)\cdot\left(\dfrac{a}{2}+\dfrac{b}{4}\right)$
	$=$	$\displaystyle \left(\dfrac{a}{2}+\dfrac{b}{4}\right)^2$

Die Seitenlängen der Ersatzscheibe sind:

$x=\dfrac{b}{2}+t_{max}=\dfrac{b}{2}+\dfrac{a}{2}-\dfrac{b}{4}=\dfrac{a}{2}+ \dfrac{b}{4}$

$y=a-t_{max}=a-\dfrac{a}{2}+\dfrac{b}{4}= \dfrac{a}{2}+\dfrac{b}{4}$

Die Ersatzscheibe ist demnach ein Quadrat.

Für den Punkt $P$ auf $[S_1; S_2]$ , von dem aus geschnitten wird gilt:

$\displaystyle \overline{S_1P}=\sqrt{t^2+t^2}=\sqrt{2}\left(\frac{a}{2}-\frac{b}{4}\right)$

Zahlenbeispiel

Am nachfolgenden Applet kannst du die Aufgabe mit den Zahlenwerten $a=5\,LE$ und $b=4\,LE$ nachvollziehen. Verschiebe dazu den Erzeugungspunkt $P$ längst der Bruchkante $[S_1S_2]$ .

Man erhält für den maximalen Flächeninhalt $12{,}25\;FE$ , für die (quadratische) Rechtecksseite $3{,}5\,LE$ und für den Abstand des Punktes $P$ von $S_1$ den Wert $1{,}5\cdot \sqrt{2}\,LE\approx{2{,}1}\,LE$

[https://www.geogebra.org/material/iframe/id/CAejsbAf]

Fall 2

$a>\dfrac{3}{2}b\Rightarrow\;t_{max}>\dfrac{b}{2}\Rightarrow\;t_{max}\notin [0;\dfrac{b}{2}]$

Damit liegt der Scheitelpunkt der Flächenparabel $A(t)$ rechts vom Intervall $[0;\dfrac{b}{2}]$ und $A(t)$ nimmt in diesem Intervall streng monoton zu.

Die größte Fläche wird demnach - als Randextremum - angenommen, wenn der erzeugende Punkt $P$ mit dem rechtem Randpunkt $S_2$ zusammenfällt. Also für $t=\dfrac{b}{2}$ .

Demnach gilt hier:

$A_{max}=A(\dfrac{b}{2})=b\cdot \left(a-\dfrac{b}{2}\right)$ .

Die Seitenlängen für $A_{max}$ sind:

$x=\dfrac{b}{2}+\dfrac{b}{2}=b\quad$ und $\quad y=a-\dfrac{b}{2}$ .

Für den erzeugenden Punkt $P$ gilt: $P=S_2$ .

Zahlenbeispiel

Am nachfolgenden Applet kannst du die Aufgabe mit den Zahlenwerten $a=6\,LE$ und $b=3\,LE$ nachvollziehen. Verschiebe dazu den Erzeugungspunkt $P$ längs der Bruchkante $[S_1S_2]$ .

Man erhält für den maximalen Flächeninhalt $13{,}5\,FE$ , bei den Seitenlängen von $a=4{,}5\,LE$ und $b=3\,LE$ .

Zusammenfassung

Die Aufgabe ist durch die notwendige Fallunterscheidung der Fenstermaße anspruchsvoll.

Falls die Fensterhöhe "nicht zu groß" gegenüber der Fensterbreite ist ( $a\leq \dfrac{3}{2}b$ ), besitzt die Aufgabe ein lokales Maximum.

Falls die Fensterhöhe "zu groß" gegenüber der Fensterbreite ist ( $a>\dfrac{3}{2}b$ ) ergibt sich ein Randmaximum.

Alternative Lösung

Die beschriebene Lösung hat für die variable Lage des Erzeugungspunktes $P$ auf der Bruchkante $[S_1S_2]$ seinen horizontalen Abstand $t$ vom Punkt $S_1$ als Parameter verwendet.

Für eine alternative Lösung der Aufgabe verzichten wir auf einen zusätzlichen Parameter und betrachten die Rechtecksseiten $x$ und $y$ als die Variablen des gesuchten maximalen Rechtecks und bestimmen die Nebenbedingung zwischen $x$ und $y$ aus dem Strahlensatz.

Die Zielfunktion lautet:

$A(x;y)=x\cdot y$ mit $x\in[b/2;b]$

Die Nebenbedingung ergibt sich durch Anwendung des Strahlensatzes in der nebenstehenden Skizze:

\displaystyle \dfrac{x}{\dfrac{b}{2}}

=

\displaystyle \dfrac{a-y+\dfrac{b}{2}}{\dfrac{b}{2}}

\displaystyle \cdot\dfrac{b}{2}

$\Rightarrow$

$\displaystyle x$	$=$	$\displaystyle a-y+\dfrac{b}{2}$
$\displaystyle y$	$=$	$\displaystyle -x+a+\dfrac{b}{2}$

Grafische Veranschaulichung

Setze das Ergebnis der Nebenbedingung in die Zielfunktion ein.

$\displaystyle A\left(x\right)$	$=$	$\displaystyle x\cdot\left(-x+a+\dfrac{b}{2}\right)$
	↓	Setze $A'(x)$ gleich Null, um ein mögliches Maximum $x_m$ zu erhalten.
$\displaystyle A\left(x\right)$	$=$	$\displaystyle -x^2+\left(a+\dfrac{b}{2}\right)\cdot x$
	↓	mit $x\in[b/2;b]$
$\displaystyle A`\left(x\right)$	$=$	$\displaystyle -2x+\left(a+\dfrac{b}{2}\right)$
$\displaystyle -2x_m+\left(a+\dfrac{b}{2}\right)$	$=$	$\displaystyle 0$
$\displaystyle x_m$	$=$	$\displaystyle \dfrac{a}{2}+\dfrac{b}{4}$

Zwischenstand der alternativen Lösung

Die gesuchte Ersatzscheibe mit maximalem Flächeninhalt ist ein Rechteck mit den Seitenlängen $x\,LE$ und $y\,LE$ .

Dabei muss $x$ eine Zahl aus dem Intervall $[b/2;b]$ sein, damit der erzeugende Punkt $P$ auf der Strecke $[S_1S_2]$ liegt.

Durch die Nebenbedingung aus dem Strahlensatz ergibt sich mit $A(x)=-x^2+(a+\dfrac{b}{2})x$ eine nach unten geöffnete Parabel und $x_m=\dfrac{a}{2}+\dfrac{b}{4}$ liefert ein lokales Maximum für die Rechtecksfläche - aber nur dann, wenn $x_m$ im Intervall $[b/2;b]$ liegt.

Da gilt: $a>b$ , ist jedenfalls

$x_m=\dfrac{a}{2}+\dfrac{b}{4}>\dfrac{b}{3}+\dfrac{b}{4}>\dfrac{b}{2}$ .

$x_m$ ist aber nicht für jedes Zahlenpaar $a$ und $b$ kleiner als $b$ , da gilt:

$\displaystyle \dfrac{a}{2}+\dfrac{b}{4}$	$≤$	$\displaystyle b$	$\displaystyle \cdot4$
$\displaystyle 2a+b$	$≤$	$\displaystyle 4b$
$\displaystyle a$	$=$	$\displaystyle \dfrac{3}{2}b$

Fallunterscheidung

Fall 1: $\quad b<a\leq\frac{3}{2}b\quad\text{"a ist nicht zu groß"}\;\Rightarrow\;x_m\in\,[\frac{b}{2};b]$

Fall 2: $a>\frac{3}{2}b\quad\text{"a beliebig groß"}\;\Rightarrow\;x_m\notin [\frac{b}{2};b]$

Fall 1: $\quad b<a\leq\frac {3}{2}b$

$x_m$ liefert lokales Maximum mit

$y_m=-\dfrac{a}{2}-\dfrac{b}{4}+a+\dfrac{b}{2}$

$y_m=\dfrac{a}{2}+\dfrac{b}{4}$

Setze $x_m$ in die Nebenbedingung ein, um $y_m$ zu bekommen. Setze beide Werte in $A(x_m;y_m)$ ein , um die maximale Fläche zu berechnen.

Das maximale Rechteck ist demnach ein Quadrat mit der Seitenlänge $\dfrac{a}{2}+\dfrac{b}{4}$ .

Für die Fläche gilt: $\quad A_{max}=(\dfrac{a}{2}+\dfrac{b}{4})^2$

Fall 2:

$a>\dfrac{3}{2}b\quad\Rightarrow\quad x_m>b\quad\Rightarrow\quad x_m\notin [\dfrac{b}{2};b]$

Damit liegt der Scheitelpunkt der Parabel $A(x)$ rechts vom Intervall $[\dfrac{b}{2};b]$ und $A(x)$ nimmt in diesem Intervall streng monoton zu.

Die größte Fläche wird demnach - als Randextremum - angenommen, wenn der erzeugende Punkt $P$ mit dem rechten Randpunkt $S_2$ zusammenfällt. Also für $x_m=b$ .

Damit gilt für die Seitenlängen des gesuchten maximalen Rechtecks $x=b$ und $y=a-\dfrac{b}{2}$ .

Die maximale Fläche ist:

$A_{max}=b\cdot (a-\dfrac{b}{2})$

Die beiden folgenden Grafiken veranschaulichen die alternative Lösung der Aufgabe.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

9
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Aus einem $36\,\mathrm{m}$ langen Draht soll das Kantenmodell einer quadratischen Säule hergestellt werden.
Wie lang sind die Kanten zu wählen, damit die Säule maximales Volumen hat?
ist die Kantenlänge.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Gegeben: Gesamtkantenlänge einer quadratischen Säule
Gesucht: Kantenlängen für maximales Volumen
$V=a^2\cdot h$
Stelle die Zielfunktion auf, die maximiert werden soll; in diesem Fall ist das das Volumen einer quadratischen Säule mit der Grundseitenlänge $a$ und der Höhe $h$ .
$4\cdot a+4\cdot h+4\cdot a=36$
Bestimme die Nebenbedingung, die durch die Gesamtkantenlänge gegeben ist.
$h=9-2a$
Stelle die Nebenbedingung nach $h$ um.
$V(a)=a^2\cdot\left(9-2a\right)$ mit $a>0$
Setze die Nebenbedingung in die Zielfunktion ein, um die Extremalfunktion zu erhalten. Beachte dabei, dass a positiv sein muss. Leite die Extremfunktion zweimal ab.
$\def\arraystretch{1.25} \begin{array}{ccc}V'(a)&=&18a-6a^2\\V''(a)&=&18-12a\end{array}$
Setze die erste Ableitung gleich Null, berechne die Grundseitenlänge und setze ihn in die zweite Ableitung ein, um zu erkennen, dass es sich tatsächlich um ein Maximum handelt.
$V'(a)=18a-6a^2=a(18-3a)=0$
$a=0$ oder $a=3$
$a=0$ muss nicht weiter untersucht werden, da nur positive Grundseitenlängen betrachtet werden.
$\def\arraystretch{1.25} \begin{array}{l}V''(3)=18-12\cdot3=-18<0\\\end{array}$
Da die zweite Ableitung negativ ist, handelt es sich bei $a=3$ um das gesuchte Maximum.
Gib nun endgültig $a$ und $h$ an und berechne das Volumen (nicht verlangt).
$a=3\;\Rightarrow h=3\Rightarrow V=27$
10
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Aus einem 120cm langen Draht ist das Kantenmodell eines Quaders herzustellen, so dass eine Kante dreimal so lang wie eine andere und der Rauminhalt maximal ist.
Wie lang sind die Kanten zu wählen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Gegeben: Gesamtkantenlänge, eine Kante dreimal so lang wie eine andere Kante
Gesucht: Kantenlänge so, dass Volumen maximal
Stelle die Volumenfunktion des Quaders mit den Kanten $a$ , $b$ und $c$ auf; das ist die Zielfunktion, die es zu maximieren gilt.
$V=a\cdot b\cdot c$
Bestimme die Nebenbedingung, welche durch die Gesamtkantenlänge und die Tatsache, dass eine Kante dreimal so lang wie eine andere Kante sein soll, gegeben ist. Wähle dabei z. B. b=3a.
$4\cdot a+4\cdot3\cdot a+4\cdot c=120$
Stelle die Nebenbedingung um.
$c=30-4a$
Setze die Nebenbedingung in die Zielfunktion ein und erhalte die Extremalfunktion. Beachte dabei, dass negative Längen keinen Sinn machen.
$V(a)=3\cdot a^2\cdot(30-4a)$ mit $a>0$
Leite die Extremalfunktion zweimal ab, um im nächsten Schritt den Extremwert und die Art des Extremwertes bestimmen zu können.
$\def\arraystretch{1.25} \begin{array}{ccc}V'(a)&=&180a-36a^2\\V''(a)&=&180-72a\end{array}$
Setze die erste Ableitung gleich Null und setze die Lösung dieser Gleichung in die zweite Ableitung ein. Du erkennst dann, dass der Extremwert tatsächlich wie gewünscht ein Maximum ist.
$V'(a)=0$
$a=5$
$V''(5)=-180<0$
Berechne nun noch die Kantenlängen $b$ und $c$ .
$\def\arraystretch{1.25} \begin{array}{l}\;\;\;\;\;\;a=5\\\Rightarrow b\;=3\cdot5=15\\\Rightarrow c\;=30-4\cdot5=10\end{array}$
Kante $a$ ist $5cm$ , Kante $b$ $15cm$ und Kante $c$ $10cm$ zu wählen.
11
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
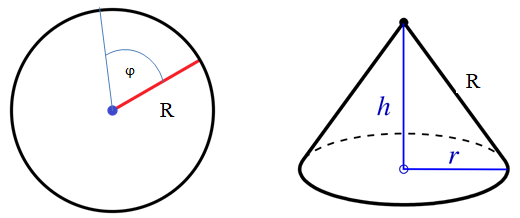
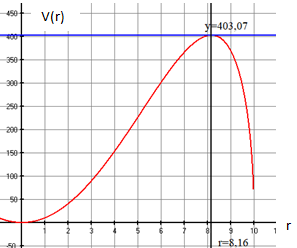
Aus einem kreisrunden Papierstück mit dem Radius R soll eine kegelförmige Popkorntüte hergestellt werden.
Wie muss das Papier zugeschnitten und zusammengeklebt werden, wenn die fertige Tüte mit möglichst viel Popcorn gefüllt werden soll?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Aus dem Kreis mit dem Radius $R$ wird ein Kreissektor mit dem Mittelpunktswinkel $\varphi$ ausgeschnitten. Der ausgeschnittene Kreissektor ergibt den Mantel des Kegels.
Aufstellen der Zielfunktion und der Nebenbedingung
Die Zielfunktion bei dieser Aufgabe ist das Volumen eines Kegels:
Die Nebenbedingung ergibt sich aus der obigen rechten Abbildung.
Im rechtwinkligen Dreieck gilt der Satz des Pythagoras:
Die Volumenfunktion $V$ hängt sowohl von $r$ als auch von $h$ ab, d.h. $V(r,h)$ .
Um die Nebenbedingung in die Zielfunktion einzusetzen kann man sie nach einer der beiden Variablen $r$ oder $h$ auflösen. Man hat somit zwei Lösungsvarianten.
Die einfachere dieser beiden Lösungsvarianten ergibt sich, wenn das Volumen $V$ des Kegels nur von der Kegelhöhe $h$ abhängig ist, d.h. es muss $V(h)$ bestimmt werden.
Lösungsvariante 1
Einsetzen in die Zielfunktion
Gleichung $\mathrm{(II)}$ wird nach $r$ bzw. gleich nach $r^2$ aufgelöst: $r^2=R^2-h^2$ .
Dieses $r^2$ wird nun in die Zielfunktion $\mathrm{(I)}$ eingesetzt um die Extremalfunktion als Funktion von $h$ zu erhalten:
$V(h) = \dfrac{1}{3}\pi\cdot (R^2-h^2)\cdot h=\dfrac{1}{3}\pi\cdot (R^2h-h^3)$ $\mathrm{(III)}$ .
Für den Definitionsbereich $\mathbb{D}$ gilt: $0<h<R$ .
Bestimmung des Extremwertes
Leite die Extremalfunktion $\mathrm{(III)}$ zweimal ab, um den Extremwert und die Art des Extremwertes bestimmen zu können.
$V'(h)=\dfrac{1}{3}\pi\cdot (R^2-3h^2)$
$V''(h) = \dfrac{1}{3}\pi\cdot (-6h)= -2\pi h<0$
Setze die erste Ableitung gleich Null: $0=\dfrac{1}{3}\pi\cdot (R^2-3h^2)\Rightarrow R^2=3h^2$
Nach $h$ aufgelöst erhält man: $h=\dfrac{R}{\sqrt{3}}$ $\mathrm{(IV)}$ .
Da $h \lt R$ ist, gilt: $h \in \mathbb{D}$ .
Setze Gleichung $\mathrm{(IV)}$ in die zweite Ableitung ein: $V''(\dfrac{R}{\sqrt{3}}) = -2\pi\cdot \dfrac{R}{\sqrt{3}}<0$
Da die zweite Ableitung kleiner Null ist, ist der Extremwert ein Maximum.
Bestimmung des Kegelgrundkreisradius
Setzt man $h=\dfrac{R}{\sqrt{3}}$ in $r^2=R^2-h^2$ ein,
so erhält man: $r^2 = R^2-(\dfrac{R}{\sqrt{3}})^2= \dfrac{2}{3}\cdot R^2$
Zieht man nun die Wurzel aus $r^2$ , so erhält man für den Radius $r$ des Grundkreises des Kegels: $r= \sqrt{\dfrac{2}{3}}\cdot R$ $\mathrm{(V)}$
Bestimmung des Mittelpunktwinkels
Für die Bogenlänge $b$ des ausgeschnittenen Kreissektors gilt: $b=\dfrac{R \cdot \pi \cdot \varphi}{180^\circ}$
Die Bogenlänge $b$ ist der Umfang des Kegelgrundkreises mit dem Radius $r$ .
$b=\dfrac{R \cdot \pi \cdot \varphi}{180^\circ}=2\pi r\Rightarrow$ nach $\varphi$ aufgelöst:
$\varphi =\dfrac{r\cdot 360^\circ}{R}$ $\mathrm{(VI)}$ .
Setzt man Gleichung $\mathrm{(V)}$ $r= \sqrt{\dfrac{2}{3}}\cdot R$ in Gleichung $\mathrm{(VI)}$ ein,
erhält man $\varphi = \sqrt{\dfrac{2}{3}}\cdot 360^\circ \approx 293{,}94^\circ$
Anmerkung: Der Winkel $\varphi$ ist von $R$ unabhängig.
Das maximale Volumen in Abhängigkeit von $R$
Setzt man die Gleichungen $\mathrm{(IV)}$ und $\mathrm{(V)}$ in Gleichung $\mathrm{(I)}$ ein, so erhält man das maximale Volumen:
$V_{max}=\dfrac{2}{9\cdot \sqrt{3}}\cdot\pi\cdot R^3$
Beantwortung der Ausgangsfrage
Die Popkorntüte hat ein maximales Volumen, wenn aus dem Kreis mit Radius $R$ ein Kreissektor mit dem Mittelpunktswinkel $\varphi \approx 293{,}94^\circ$ ausgeschnitten wird.
Der Radius des Kegelgrundkreises beträgt $r= \sqrt{\dfrac{2}{3}}\cdot R$ .
Die Höhe des Kegels beträgt $h=\dfrac{R}{\sqrt{3}}$ und sein maximales Volumen ist
$V_{max}=\dfrac{2}{9\cdot \sqrt{3}}\cdot\pi\cdot R^3$ .
Lösungsvariante 2
Einsetzen in die Zielfunktion
Löst man Gleichung $\mathrm{(II)}$ nach $h$ auf, erhält man: $h=\sqrt{R^2-r^2}$ $\mathrm{(VII)}$
Setzt man Gleichung $\mathrm{(VII)}$ in Gleichung $\mathrm{(I)}$ ein, erhält man das Volumen in Abhängigkeit von $r$ : $V(r) = \dfrac{1}{3}\pi\cdot r^2\cdot\sqrt{R^2-r^2} \mathrm{(VIII)}$
Für den Definitionsbereich $\mathbb{D}$ gilt: $0 \lt r\lt R$ .
Anmerkung: Für $r=0$ und $r=R$ ist das Volumen gleich Null.
Bestimmung des Extremwertes
Leite die Extremalfunktion $\mathrm{(VIII)}$ zweimal ab, um den Extremwert und die Art des Extremwertes bestimmen zu können. Für diese Ableitung benötigst du die Produktregel, die Ableitung einer Wurzel und die Kettenregel. Der Rechenaufwand für diese Ableitung ist relativ hoch. Mit einem Rechentrick kann man den Rechenaufwand verringern. Der Funktionsterm wird so umgeformt, dass der Term $r^2$ unter die Wurzel gezogen wird. Man erhält Gleichung $\mathrm{(IX)}$ .
$V(r) = \dfrac{1}{3}\pi\cdot \sqrt{r^4(R^2-r^2)}=\dfrac{1}{3}\pi\cdot \sqrt{R^2 \cdot r^4-r^6}$ $\mathrm{(IX)}$
Für die Ableitung von Gleichung $\mathrm{(IX)}$ genügt die Betrachtung des Radikanden.
Nimmt der Radikand einen maximalen Wert an, so ist auch die Wurzel aus diesem maximalen Radikanden ebenfalls maximal. Damit ist auch $V(r)$ maximal.
Wir betrachten nun den Radikanden als Funktion von $r$ .
$f(r) = R^2 \cdot r^4 - r^6$ und suchen das Maximum dieser Funktion.
$f'(r) = 4 \cdot R^2 \cdot r^3 - 6 \cdot r^5$
$f''(r) = 12 \cdot R^2 \cdot r^2 - 30 \cdot r^4$
Setze die erste Ableitung gleich Null:
$0= 4 \cdot R^2 \cdot r^3 - 6 \cdot r^5=2 \cdot r^3(2 \cdot R^2-3 \cdot r^2)$
Die Gleichung hat die Lösungen $r=0$ (entfällt hier, da $V(0)=0$ ) und die Lösung
$r= \sqrt{ \dfrac{2}{3}} \cdot R$ $\mathrm{(X)}$
Da $0 \lt r \lt R$ ist, gilt $r \in \mathbb{D}$ .
Zur Überprüfung, ob es sich um ein Maximum handelt, setze Gleichung $\mathrm{(X)}$ in die zweite Ableitung ein:
$f''(\sqrt{ \dfrac{2}{3}} \cdot R) = 12 \cdot R^2 \cdot \dfrac{2}{3} \cdot R^2 - 30 \cdot \dfrac{4}{9} \cdot R^4=8 \cdot R^4- \dfrac{40}{3} \cdot R^4 =$
$- \dfrac{16}{3} \cdot R^4 \lt 0$
Da die zweite Ableitung kleiner Null ist, ist der Extremwert ein Maximum.
Bestimmung der Höhe des Kegels
In Gleichung $\mathrm{(VII)}$ $h=\sqrt{R^2-r^2}$ wird die Gleichung $\mathrm{(X)}$ $r= \sqrt{ \dfrac{2}{3}} \cdot R$ eingesetzt:
$h=\sqrt{R^2- \dfrac{2}{3} \cdot R^2} =\sqrt{\dfrac {1}{3}R^2} = \dfrac{R}{\sqrt{3}}$ $\mathrm{(XI)}$
Bestimmung des Mittelpunktswinkels
In Gleichung $\mathrm{(VI)}$ $\varphi =\dfrac{r\cdot 360^\circ}{R}$ wird die Gleichung $\mathrm{(X)}$ $r= \sqrt{ \dfrac{2}{3}} \cdot R$ eingesetzt $\Rightarrow$ $\varphi = \sqrt{\dfrac{2}{3}}\cdot 360^\circ \approx 293{,}94^\circ$ .
Anmerkung: der Winkel $\varphi$ ist von $R$ unabhängig.
Das maximale Volumen in Abhängigkeit von $R$
Setzt man die Gleichung $\mathrm{(X)}$ $r= \sqrt{ \dfrac{2}{3}} \cdot R$ in Gleichung $\mathrm{(VIII)}$ ein, so erhält man das maximale Volumen in Abhängigkeit von $R$ : $V_{max}=\dfrac{2}{9\cdot \sqrt{3}}\cdot\pi\cdot R^3$ .
Beantwortung der Ausgangsfrage
Die Popkorntüte hat ein maximales Volumen, wenn aus dem Kreis mit Radius $R$ ein Kreissektor mit dem Mittelpunktswinkel $\varphi \approx 293{,}94 ^\circ$ ausgeschnitten wird.
Der Radius des Kegelgrundkreises ist $r= \sqrt{\dfrac{2}{3}}\cdot R$ .
Die Höhe des Kegels beträgt $h=\dfrac{R}{\sqrt{3}}$ und sein maximales Volumen ist
$V_{max}=\dfrac{2}{9\cdot \sqrt{3}}\cdot\pi\cdot R^3$ .
Beispiel
Für einen Kreisradius von $R = 10\, \mathrm{cm}$ ergibt sich ein Kegelgrundkreisradius von
$r \approx 8{,}16\, \mathrm{cm}$ , eine Kegelhöhe von $h \approx 5{,}77\, \mathrm{cm}$ und ein Mittelpunktswinkel
von $φ = 293{,}94^\circ$ .
Das maximale Volumen in diesem Beispiel beträgt $V_{max}\approx 403{,}07\, \mathrm{cm^3}.$
In der Abbildung ist die Extremalfunktion
$V(r) = \dfrac{1}{3}\pi\cdot r^2\cdot\sqrt{R^2-r^2}$
für $R = 10 \mathrm{cm}$ dargestellt.
Das Extremum befindet sich im Punkt
$(8{,}16\vert 403{,}07)$ .
Mit den Maßen $R = 10\, \mathrm{cm}$ und
$φ = 293{,}94^\circ$ wurde ein Kegel hergestellt.
Unter dem Kegel befindet sich ein Lineal
zur Bestimmung des Durchmessers.
In diesem Bild ist die rechte Seite des Lineals zu sehen.
Es zeigt einen Durchmesser von
$\approx 163{,}4\, \mathrm{mm}$ an. Der Radius beträgt
$\approx 8{,}17\, \mathrm{cm}$ in guter Übereinstimmung mit dem berechneten Wert.
Bestimme die Zielfunktion und die Nebenbedingung. Ermittle daraus die Extremalfunktion und bestimme mit Hilfe der Ableitung den Extremwert.

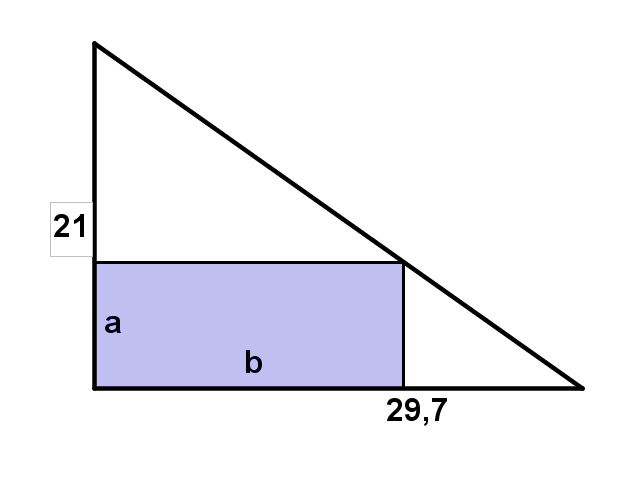
Aus einem diagonal halbierten DIN A4 Blatt soll entsprechend der Zeichnung ein möglichst großflächiges Rechteck geschnitten werden.

Finde die Breite a, für die der Flächeninhalt des Rechtecks maximal ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

Stelle die allgemeine Flächenformel eines Rechtecks auf.

$\mathrm A=\mathrm a\cdot\mathrm b$

Bestimme b. Benutze dazu, dass das ganze Dreieck ähnlich zu dem schraffierten Dreieck ist und berechne mit dem SWS-Satz (oder: Strahlensatz V-Figur) die Seite b.

$\displaystyle \frac{\mathrm{b}}{\left(21-\mathrm{a}\right)}$	$=$	$\displaystyle \frac{29{,}7}{21}$
	↓	Löse nach b auf.
$\displaystyle b$	$=$	$\displaystyle \frac{29{,}7}{21}\cdot\left(21-\mathrm{a}\right)$
	↓	Setze b in die allgemeine Form für den Flächeninhalt des Rechtecks ein.
$\displaystyle A$	$=$	$\displaystyle \mathrm{a}\cdot\frac{29{,}7}{21}\cdot\left(21-\mathrm{a}\right)$
	$=$	$\displaystyle \mathrm{a}\left(29{,}7-\frac{29{,}7}{21}\mathrm{a}\right)$
	$=$	$\displaystyle 29{,}7\mathrm{a}-\frac{29{,}7}{21}\mathrm{a}^2$

Dies ist nun die Formel für den Flächeninhalt des Rechtecks in Abhängigkeit von a.

Bestimme nun den maximalen Flächeninhalt.

Da es sich um eine nach unten geöffnete Parabel handelt, liegt das Maximum der Funktion bei ihrem Scheitelpunkt .

Dieser liegt genau in der Mitte zwischen den beiden Nullstellen.

Bestimme die Nullstellen der Funktion.

$\displaystyle -\frac{29{,}7}{21}\mathrm{a}^2+29{,}7\mathrm{a}$	$=$	$\displaystyle 0$
$\displaystyle \mathrm{a}\left(29{,}7-\frac{29{,}7}{21}\mathrm{a}\right)$	$=$	$\displaystyle 0$

Betrachte die beiden Faktoren getrennt. Betrachte zuerst den 1. Faktor:

$\Rightarrow\;\;{\mathrm a}_1=0$

Betrachte den 2. Faktor:

$\displaystyle 29{,}7-\frac{29{,}7}{21}\mathrm{a}$	$=$	$\displaystyle 0$	$\displaystyle +\frac{29{,}7}{21}a$
$\displaystyle 29{,}7$	$=$	$\displaystyle \frac{29{,}7}{21}\mathrm{a}$	$\displaystyle :\frac{29{,}7}{21}$

$\Rightarrow\;\;{\mathrm a}_2=21$

Bestimme die Stelle, an der der Scheitelpunkt liegt (Mitte der Nullstellen).

$\Rightarrow$ Scheitel bei $\mathrm a=10{,}5$

Formuliere einen Antwortsatz.

Für $\mathrm a=10{,}5$ wird der Flächeninhaltdes Rechtecks maximal.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

13
Zwischen einer Straße und einem Bach soll als Hochwasserschutz ein Damm errichtet werden.
Aus technischen Gründen ist dies aber nur möglich, wenn der Bach der Straße auf höchstens 5 m nahekommt.
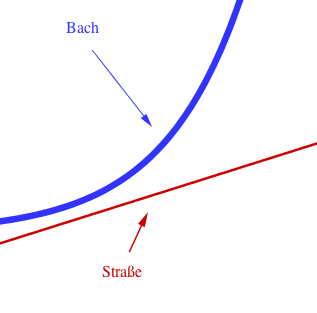
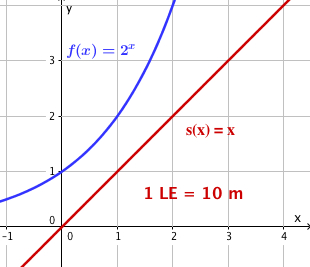
Berechne, ob der Schutzdamm bei dem gegebenen Geländeplan (1LE = 10 m) gebaut werden kann, wenn der Bach dem Graphen der Funktion $f(x)=2^x$ und die Straße dem Graphen der Funktion $s(x)=x$ folgen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Berechne den Abstand d(x) eines beliebigen Punktes $P(x\vert2^x)$ des Bachs von der Straße.
Benutze dazu im gleichschenkligen Dreieck den Satz des Pythagoras.
$d^2(x)+d^2(x)=\left(2^x-x\right)^2$
$d^2(x)=\frac12\cdot\left(2^x-x\right)^2$
$d(x)=\frac1{\sqrt2}\cdot\left(2^x-x\right)$
Um das Minimum von $d(x)$ zu berechnen, brauchst du mit Hilfe der Ableitung der Exponentialfunktion $2^x$ die Ableitung $d'(x)$ .
$d'(x)=\frac1{\sqrt2}\left(\ln(2)\cdot2^x-1\right)$
Setze $d'(x)=0$ um das Minimum von d(x) zu berechnen.
$\frac1{\sqrt2}\cdot\left(\ln(2)\cdot2^x-1\right)=0$
der 2. Faktor muss 0 werden
$\;\;\;\;\;\;\;\;\;\ln(2)\cdot2^x-1=0$
nach $2^x$ auflösen
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\displaystyle 2^x=\frac1{\ln(2)}$
nach x mit Hilfe einer Logarithmusfunktion auflösen
$\displaystyle x=\frac1{\ln(2)}\cdot\ln\left(\frac1{\ln(2)}\right)$
$x\approx0{,}53$
Noch fehlt der Nachweis, dass $x\approx0{,}53$ tasächlich ein Abstandsminimum liefert.
Da $2^x$ streng monton steigend ist, gilt: $d'(0{,}53-h)<0$ und $d'(0{,}53+h)>0$ .Damit liefert $x\approx0{,}53$ das Abstandsminimum.
Berechne $d(0{,}53)$ .
$d(0{,}53)=\frac1{\sqrt2}\left(2^{0{,}53}-0{,}53\right)$
$d(0{,}53)\approx0{,}65$
Der Bach kommt der Straße auf rund 6,50 m nahe. Der Schutzdamm kann deshalb gebaut werden.
Bestätige das Rechenergebnis am nebenstehenden Applet.
Verschiebe dazu den Punkt P auf dem Fluss und lies den jeweiligen Abstand d zur Straße ab. Beachte dabei: 1 LE = 10 m.
alternative Lösung
Berechne denjenigen Punkt der Exponentialfunktion f, in dem die Steigung 1 ist. Der Abstand dieses Punktes von der Geraden s ist das gesuchte Abstandsminimum.
Bilde die Ableitung der Exponentialfunktion.
$f(x)=2^x\Rightarrow f'(x)=\ln(2)\cdot2^x$
Setze $f'(x)$ gleich 1.
$\ln(2)\cdot2^x=1$
Teile durch $\ln(2)$
$\displaystyle 2^x=\frac1{\ln(2)}$
Löse die Gleichung durch Logarithmieren.
$\displaystyle x=\frac1{\ln(2)}\cdot\ln\left(\frac1{\ln(2)}\right)$
Einsatz des Taschenrechners.
$x\approx0{,}53$
Setze $x=0{,}53$ und berechne den Näherungswert der y-Koordinate.
$P(0{,}53\vert1{,}44)$
Den Abstand des Punktes $P(0{,}53\vert1{,}44)$ von der Geraden $s:\;y\;-\;x\;=\;0$ berechnet man am bequemsten mit der Hessesche Normalenform der Geraden.
HNF von s:
Du erhältst den gesuchten Abstand $d(P;s)$ , wenn du die Koordinaten von P in die linke Seite der HNF einsetzt.
$d_{min}=\;d(P;s)\approx0{,}64$
Der geringfügige Unterschied zum ersten Ergebnis resultiert aus dem Rundungswert der y-Koordinate von P.
14
Gegeben sind die beiden Parabeln mit den Funktionsgleichungen
$\mathrm{f}(\mathrm{x})=4-\mathrm{x}^2$ und $\mathrm g(\mathrm x)=\left(\mathrm x-2\right)^2-6$
1. Zeichne die beiden Graphen sauber in ein Koordinatensystem
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel zeichnen
  $\def\arraystretch{1.25} \begin{array}{ccc}f(x)&=&4-x^2\\g(x)&=&(x-2)^2-6\end{array}$
  Zeichne die Parabeln ein. Verwende dazu entweder die Technik aus dem verlinkten Artikel oder benutze eine Wertetabelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne die Schnittpunkte der beiden Parabeln
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
  $\def\arraystretch{1.25} \begin{array}{ccc}f(x)&=&4-x^2\\g(x)&=&(x-2)^2-6\end{array}$
  Setze die beiden Funktionen gleich.
  $4-x^2=(x-2)^2-6$
  Bringe die quadratische Gleichung auf allgemeine Form
  $2x^2-4x-6=0$
  Berechne die Diskriminante .
  $D=b^2-4ac=(-4)^2-4\cdot 2\cdot (-6)=64$
  Die Gleichung hat also zwei Lösungen, die mit Hilfe der Mitternachtsformel berechnet werden können.
  $x_{1{,}2}=\frac{4\pm\sqrt D}4=\frac{4\pm8}4\Rightarrow x_1=3,\;x_2=-1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Zeichnet man im Bereich $-1<x<3$ senkrechte Verbindungsstrecken von der oberen zur unteren Parabel, so haben diese Strecken unterschiedliche Längen.
  Bestimme die Strecke mit der größten Länge! Zeichne diese Strecke in dein Bild ein!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
  $\def\arraystretch{1.25} \begin{array}{ccc}f(x)&=&4-x^2\\g(x)&=&(x-2)^2-6\end{array}$
  Zu maximieren ist der Abstand zwischen den beiden Funktionen; die Extremalfunktion bestimmst du also mit $f(x)-g(x)$ , da $f$ im Bereich $-1<x<3$ größer als $g$ ist.
  $E(x)=f(x)-g(x)=-2x^2+4x+6$
  Leite diese Funktion zweimal ab , um die Extremstelle bestimmen zu können.
  $\def\arraystretch{1.25} \begin{array}{ccc}E'(x)&=&-4x+4\\E''(x)&=&-4\end{array}$
  Setze die erste Ableitung gleich Null , berechne x und setze in die zweite Ableitung ein, um zu erkennen, dass es sich tatsächlich um ein Maximum handelt.
  $E'(x)=-4x+4=0$
  $x=1$
  $E''(1)=-4$
  $E(1)=8$
  Die längste zwischen den Graphen verlaufende senkrechte Strecke ist also bei $x=1$ zu finden. Ihre Länge beträgt $8$ Längeneinheiten.
  Nun musst du diese Strecke nur noch in die Zeichnung von Teilaufgabe a) einzeichnen. In der Grafik ist sie gestrichelt eingetragen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

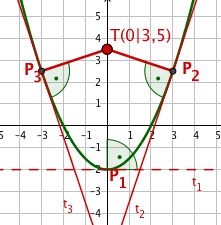
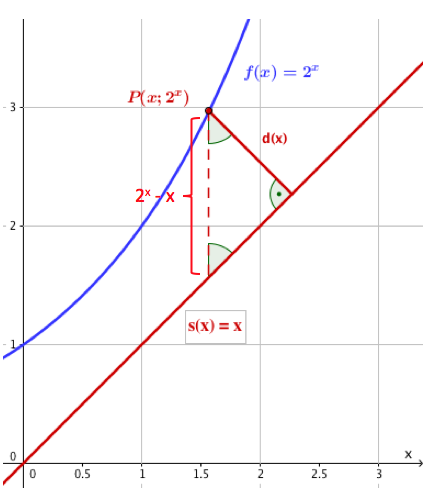
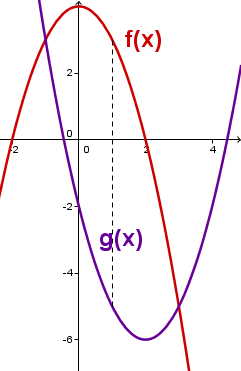
Das Bild zeigt eine Gerade $g$ und eine Parabel $p$ .

Bestimme von Gerade und Parabel jeweils die Funktionsgleichung. Berechne dann die Schnittpunkte der beiden Graphen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung

Aus dem Graphen lassen sich zwei Punkte $P_1(0\mid 0),P_2(6 \mid 6)$ der Geraden und drei Punkte $P_3(0 \mid 0), P_4(4 \mid 8), P_5(8 \mid 0)$ der Parabel ablesen.

Stelle die allgemeine Geradengleichung auf und setze die zwei bekannten Punkte ein.

$y = mx + t$

$0 = m\cdot 0 + t$

Der erste Punkt führt zu $t=0$ . Setze nun den zweiten Punkt ein.

$\displaystyle 6$	$=$	$\displaystyle m\cdot6+0$	$\displaystyle :6$
$\displaystyle m$	$=$	$\displaystyle 1$

Der zweite Punkt führt zu $m=1$ . Folglich lautet die Funktionsgleichung für die Gerade:

\displaystyle y = x.

Bestimme nun die Funktionsgleichung für die Parabel. Hierzu verwende die allgemeine Form.

$y=ax^2+bx+c$

Setze in diese Gleichung die bekannten Punkte ein.

$0 = a \cdot 0² + b \cdot 0 + c$

Der erste Punkt führt zu $c=0$ $\;\Rightarrow\;y=ax^2+bx$ .

Setze nun den zweiten Punkt $(4|8)$ ein.

$\displaystyle 8$	$=$	$\displaystyle a\cdot4^2+b\cdot4$	$\displaystyle -a\cdot4^2$
	↓	$4^2=16$
$\displaystyle 8-a\cdot16$	$=$	$\displaystyle b\cdot4$	$\displaystyle :4$
$\displaystyle b$	$=$	$\displaystyle 2-4\cdot a$

Der zweite Punkt führt zu einer Gleichung in Abhängigkeit von $a$ und $b$ . Setze nun den dritten Punkt $(8|0)$ ein.

$\displaystyle 0$	$=$	$\displaystyle a\cdot8^2+b\cdot8$
	↓	Setze die aus dem vorherigen Schritt bekannte Gleichung $b = 2-4\cdot a$ ein.
	$=$	$\displaystyle a\cdot8^2+(2-4\cdot a)\cdot8$
	↓	Berechne das Quadrat und löse die Klammer auf.
	$=$	$\displaystyle 64a+16-32a$
	↓	Fasse die Terme zusammen.
	$=$	$\displaystyle 32a+16$	$\displaystyle -16$
$\displaystyle -16$	$=$	$\displaystyle 32a$	$\displaystyle :32$
$\displaystyle a$	$=$	$\displaystyle -0{,}5$

Errechne daraus $b$ .

$b = 2 - 4 \cdot (-0.5) = 4$

Insgesamt lautet damit die Funktionsgleichung der Parabel:

\displaystyle y = x.

Schnittpunkte berechnen

Zur Berechnung der Schnittpunkte setzt man die beiden Funktionsgleichungen gleich.

$\displaystyle x$	$=$	$\displaystyle -0{,}5x^2+4x$	$\displaystyle -x$
$\displaystyle 0$	$=$	$\displaystyle -0{,}5x^2+3x$
	↓	Klammere $x$ aus.
	$=$	$\displaystyle x\left(-0{,}5x+3\right)$

Die rechte Seite ist genau dann $0$ , wenn einer der beiden Faktoren $0$ ist.

$\Rightarrow\ x_1=0$

$-0{,}5x+3=0\ \Leftrightarrow\ x_2=6$

Die Schnittpunkte sind also an den Stellen $x_1 = 0$ und $x_2 = 6$ . Die Schnittpunkte sind also

$S_1(0\mid0)$

$S_2(6 \mid 6)$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Gib die Koordinaten eines Punktes $P$ auf der Parabel nur in Abhängigkeit von ${\mathrm x}_\mathrm p$ an. Zeichnet man für $0 < x_p < 6$ zwischen dem Punkt $P$ und der Geraden $g$ zur y-Achse parallele Strecken, so sind diese Strecken unterschiedlich lang. Bestimme unter diesen Strecken die längste.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Koordinaten eines Punktes $P$ auf der Parabel
Ein Punkt auf der Parabel hat nach der Funktionsgleichung die Koordinaten $P(x_p \mid -0{,}5x_p^2 + 4x_p)$ .
Längste Strecke
Die Länge $S(x)$ der Strecke an der Stelle $x$ ergibt sich als Differenz der beiden Funktionswerte.
$S(x) = -0{,}5x^2 + 4x - x$
Nullstellen der 1. Ableitung sind mögliche Maximalstellen.
$S'(x) = -x + 3 = 0$
$x=3$ ist also die einzige Extremstelle. Mit der 2. Ableitung lässt sich überprüfen, ob hier ein Maximum vorliegt.
$S''(x)=-1$
$S''(3) = -1 < 0$
Damit liegt an der Stelle $x=3$ ein Maximum vor. Die längste Strecke hat damit die Länge
$S(3) = -0{,}5 \cdot 3^2 + 3 \cdot 3 = 4{,}5$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

16
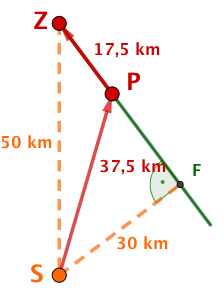
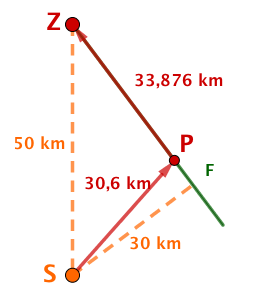
Eine Wüstenrallye gewinnt
bei einer "traditionellen" Rallye, wer als Erster am Ziel ankommt,
bei einer "alternativen" Rallye, wer den geringsten Bezinverbrauch hat.
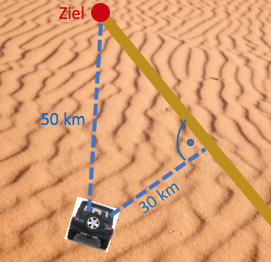
Vor dem Start steht das Team vor folgendem Problem:
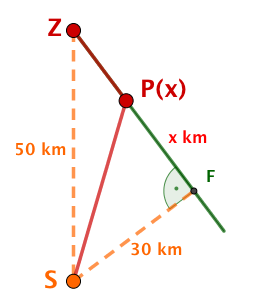
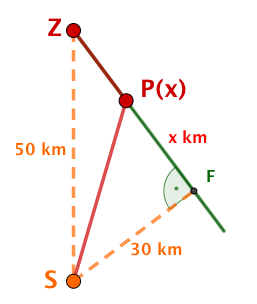
Der Startort liegt mitten in der Wüste und ist $50\,\text{km}$ vom Zielort entfernt.
Der direkte Weg zum Ziel führt durch den Wüstensand. Dort kann das Fahrzeug des Teams eine Durchschnittsgeschwindigkeit von $60\,\text{km/h}$ bei einem Durchschnittsverbrauch von $20\,\text{Liter/100km}$ erreichen.
In $30\,\text{km}$ Entfernung vom Standort führt allerdings eine schnurgerade Karawanenstraße zum Zielort. Dort könnte das Fahrzeug eine Durchschnittsgeschwindigkeit von $100\,\text{km/h}%$ bei einem Durchschnittsverbrauch von nur $4\,\text{Liter/100km}$ fahren.
1. Welche Route wird das Team bei der traditionellen Rallye wählen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
  Es gewinnt im Teil A das schnellste Team, im Teil B das Team mit dem geringsten Bezinverbrauch.
  A. Die traditionelle Rallye
  Gegeben:
  Sandstrecke: $\overline{SZ}=50\,\text{km}$
  
  Entfernung Startpunkt $S$ von der Karawanenstraße: $30\,\text{km}$
  Geschwindigkeit im Wüstensand: $v_1=60\,\text{km/h}$
  Geschwindigkeit auf der Straße: $v_2=100\,\text{km/h}$
  Vorüberlegungen:
  Die Geschwindigkeitsformeln:
  Die Entfernung des Startpunktes $S$ von der Karawanenstraße beträgt $30\,\text{km}$ . Dann ist $F$ der Lotfußpunkt mit $\overline{AF}=30\,\text{km}$ .Nach dem Satz des Pythagoras gilt dann:
  Fährt das Rallyeteam von $A$ über $F$ nach $Z$ , dann beträgt diese Fahrzeit:
  Fährt das Rallyeteam vom Startpunkt $S$ geradlinig im Wüstensand zum Zielpunkt $Z$ , dann beträgt die Fahrzeit:
  Für das Rallyeteam bringt der Umweg über $F$ also keinen Gewinn. Es könnte aber einen Punkt $P(x)$ irgendwo auf der Strecke zwischen $F$ und $Z$ geben, so dass die Fahrzeit von $50\,\text{min}$ unterboten wird.
  Die Zielfunktion $f(x)$
  Gesamtfahrzeit $f(x)$ = Fahrzeit von $A$ nach $P$ + Fahrzeit von $P$ nach $Z$ .
  Berechne $\overline{SP(x)}$ mit dem Satz des Pythagoras in Abhängigkeit von $x$ .
  Setze $\overline{SP(x)}$ in $f(x)$ ein. (Gib $f(x)$ ohne Benennungen an).
  Der Definitonsbereich für $f$ ist $[0;40]$ .
  Berechne $f'(x)$ . Benutze dabei auch die Kettenregel.
  Setze $f'(x)$ gleich Null.
  Überprüfe mit $f''(x)$ , ob ein lokales Minimum vorliegt. Berechne dazu zunächst $f''(x)$ :
  Setze dann $x_1$ ein.
  $f''(x_1) = \dfrac{15}{(900+x_1^2)^{1{,}5}} >0$ $\qquad\Rightarrow$ $x_1$ liefert minimale Fahrzeit.
  Berechne nun mit $f(x_1)$ die minimale Fahrzeit.
  $f(x)$ misst die Fahrzeit in Stunden.
  Ergebnis:
  Das Team gewinnt die traditionelle Rallye, wenn es über den $22{,}5\,\text{km}$ von $F$ entfernten Punkt $P$ der Karawanenstraße zum Ziel fährt. Es braucht dafür $48\,\text{Minuten}$ .
  Die notwendige Ansteuerung des Zwischenpunktes $P$ wird das Team natürlich mit einer Navigationshilfe vornehmen.
  Im nachfolgenden Applet kannst du die Gesamtfahrzeit $t$ in Abhängigkeit vom Zwischenpunkt $P$ nachvollziehen.
  Klicke auf den Punkt $P$ und verschiebe ihn im Intervall [0;40].
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Welche Route wird das Team bei einer alternativen Rallye wählen, wenn es jede Route zwischen Startort, Straße und Zielort fahren kann? Nach welcher Zeit bzw. mit welchem Verbrauch wird es jeweils das Ziel erreichen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
  B. Die alternative Rallye
  Gegeben:
  Benzinverbrauch im Sand:
  $20\,\text{Ltr/100km}$
  Benzinverbrauch auf der Karawanenstraße:
  $4\,\text{Ltr/100km}$
  Die Zielfunktion $f(x)$
  Gesamtverbrauch $f(x)$ = Verbrauch von $S$ nach $P$ + Verbrauch von $P$ nach $Z$ .
  $f(x)=\color{red}{0{,}2}\cdot\sqrt{900+x^2}+\color{green}{0{,}04}\cdot(40-x)$
  Der Definitionsbereich für $f$ ist $[0;40]$ .
  Verzicht auf die Benennung der Größen im Funktionsterm. Bilde $f'(x)$ .
  $f'(x)=\displaystyle\frac{0{,}2x}{\sqrt{900+x^2}}-0{,}04$
  Setze $f'(x)$ gleich Null und löse die Gleichung.
  Überprüfe mit $f''(x)$ , ob ein lokales Minimum vorliegt.
  Setze $x_1$ ein.
  $f(x_1)\gt0$ $\qquad \Rightarrow$ $x_1$ liefert minimalen Verbrauch.
  Berechne mit $f(x_1)$ den minimalen Verbrauch.
  $f(x)$ misst den Verbrauch in Liter.
  Ergebnis:
  Das Team gewinnt die alternative Rallye, wenn es über den $6{,}124\,\text{km}$ von $F$ entfernten Punkt $P$ der Karawanenstraße zum Zielpunkt fährt. Es verbraucht dabei rund $7{,}5\ \text{Liter}$ Benzin.
  Im nachfolgenden Applet kannst du den Gesamtbenzinverbrauch $v$ in Abhängigkeit vom Zwischenpunkt $P$ nachvollziehen.
  Klicke auf den Punkt $P$ und verschiebe ihn im Intervall [0;40].
  Interpretation der Ergebnisse
  Geschwindigkeitsrallye
  Verbrauchsrallye
  Das Rallyeteam nützt bei der traditionellen Rallye (Fahrzeit $48\ Min$ .; Verbrauch $8{,}7\ Liter$ ) die Karawanenstraße weit weniger als bei der alternativen (Fahrzeit rund 51 Min.; Verbrauch $7{,}5\ Liter$ ).
  Dies hängt damit zusammen, dass der "Geschwindigkeitsvorteil" der Straße ( $120\,\text{km/h}:60\,\text{km/h}$ ) weniger ausgeprägt ist, als der "Verbrauchsvorteil" ( $20\,\text{Liter/100 km}:4\,\text{Liter/100 km}$ ).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \dfrac{a}{b}$	$=$	$\displaystyle \dfrac{a-y}{x}$	$\displaystyle \left(Strahlensatz\ V-Figur\right)$
	↓	Löse nach $y$ auf.
$\displaystyle y$	$=$	$\displaystyle \dfrac{a}{b}\left(b-x\right)$
	↓	Setze in die Flächenfunktion ein.

$\displaystyle A$	$=$	$\displaystyle \dfrac{ab}{4}$
	↓	Setze die Werte ein und berechne die Fläche.
	$=$	$\displaystyle \dfrac{32m\cdot48m}{4}$
	$=$	$\displaystyle 384m^2$

Aufgaben zu Extremwerten

Alternative Lösung

Abstand eines Punktes von einer Geraden

Alternative Lösung

Alternative Lösung 1

Alternative Lösung 2

Vertiefung der Aufgabe

Weitere Lösungsmöglichkeit über die Ableitung von A(xP)A(x_P)A(xP​)

Zwischenstand der Lösung:

Fallunterscheidung:

Fall 1:

Zahlenbeispiel

Fall 2

Zahlenbeispiel

Zusammenfassung

Alternative Lösung

Zwischenstand der alternativen Lösung

Fallunterscheidung

Fall 1:b<a≤32b"a ist nicht zu groß" ⇒ xm∈ [b2;b]\quad b<a\leq\frac{3}{2}b\quad\text{"a ist nicht zu groß"}\;\Rightarrow\;x_m\in\,[\frac{b}{2};b]b<a≤23​b"a ist nicht zu groß"⇒xm​∈[2b​;b]

Fall 2: a>32b"a beliebig groß" ⇒ xm∉[b2;b]a>\frac{3}{2}b\quad\text{"a beliebig groß"}\;\Rightarrow\;x_m\notin [\frac{b}{2};b]a>23​b"a beliebig groß"⇒xm​∈/[2b​;b]

Fall 1: b<a≤32b\quad b<a\leq\frac {3}{2}bb<a≤23​b

Fall 2:

Aufstellen der Zielfunktion und der Nebenbedingung

Lösungsvariante 1

Einsetzen in die Zielfunktion

Bestimmung des Extremwertes

Bestimmung des Kegelgrundkreisradius

Bestimmung des Mittelpunktwinkels

Das maximale Volumen in Abhängigkeit von RRR

Beantwortung der Ausgangsfrage

Lösungsvariante 2

Einsetzen in die Zielfunktion

Bestimmung des Extremwertes

Bestimmung der Höhe des Kegels

Bestimmung des Mittelpunktswinkels

Das maximale Volumen in Abhängigkeit von RRR

Beantwortung der Ausgangsfrage

alternative Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Schnittpunkte berechnen

Hast du eine Frage oder Feedback?

Koordinaten eines Punktes PPP auf der Parabel

Längste Strecke

Hast du eine Frage oder Feedback?

A. Die traditionelle Rallye

Vorüberlegungen:

Die Zielfunktion f(x)f(x)f(x)

Ergebnis:

Hast du eine Frage oder Feedback?

B. Die alternative Rallye

Die Zielfunktion f(x)f(x)f(x)

Ergebnis:

Interpretation der Ergebnisse

Hast du eine Frage oder Feedback?

Weitere Lösungsmöglichkeit über die Ableitung von $A(x_P)$

Fall 1: $\quad b<a\leq\frac{3}{2}b\quad\text{"a ist nicht zu groß"}\;\Rightarrow\;x_m\in\,[\frac{b}{2};b]$

Fall 2: $a>\frac{3}{2}b\quad\text{"a beliebig groß"}\;\Rightarrow\;x_m\notin [\frac{b}{2};b]$

Fall 1: $\quad b<a\leq\frac {3}{2}b$

Das maximale Volumen in Abhängigkeit von $R$

Das maximale Volumen in Abhängigkeit von $R$

Koordinaten eines Punktes $P$ auf der Parabel

Die Zielfunktion $f(x)$

Die Zielfunktion $f(x)$