Gemischte Aufgaben zu quadratischen Funktionen
Hier findest du gemischte Aufgaben zum Thema quadratischen Funktionen. Schaffst du sie alle?
- 1
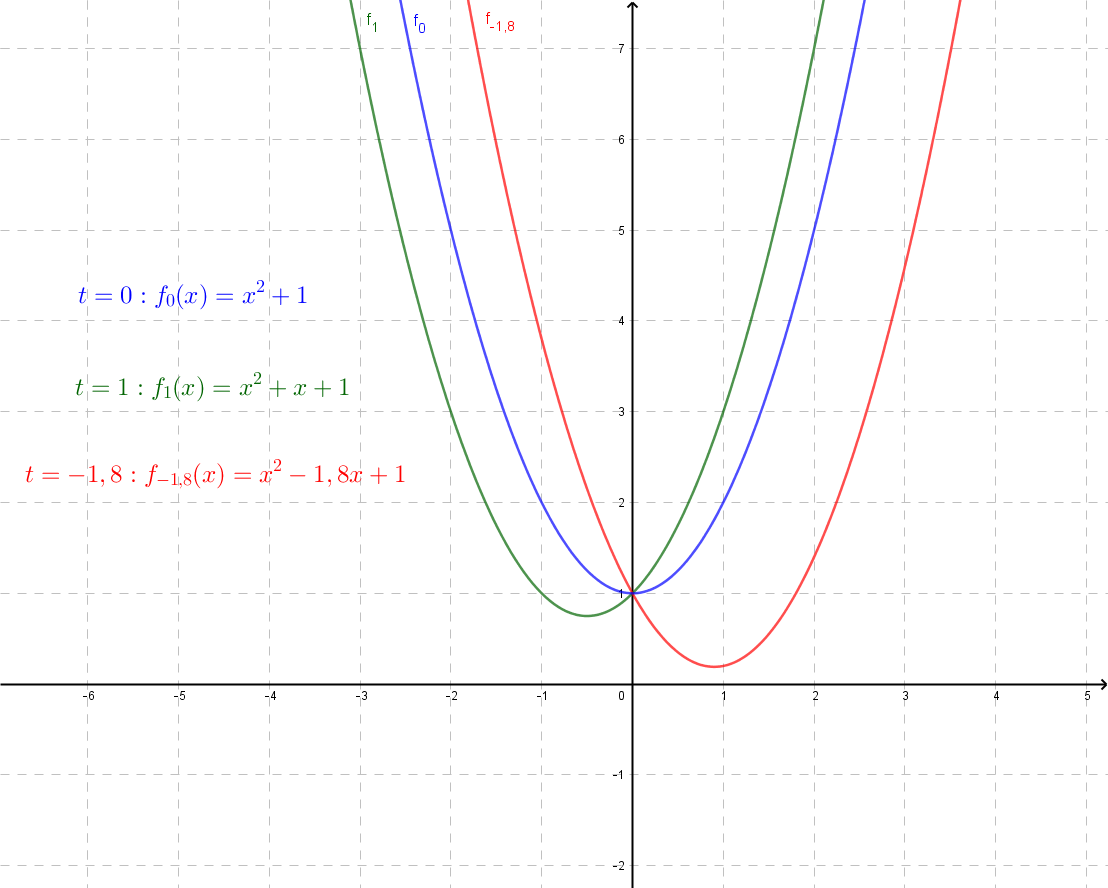
Welche Werte kann der Parameter t annehmen, so dass die folgenden Aussagen richtig sind?
Der Graph der Funktion f mit verläuft vollständig oberhalb der x-Achse.
Der Scheitel des Graphen der Funktion f mit liegt auf der x-Achse.
Der Scheitel des Graphen der Funktion f mit liegt auf der y-Achse.
- 2
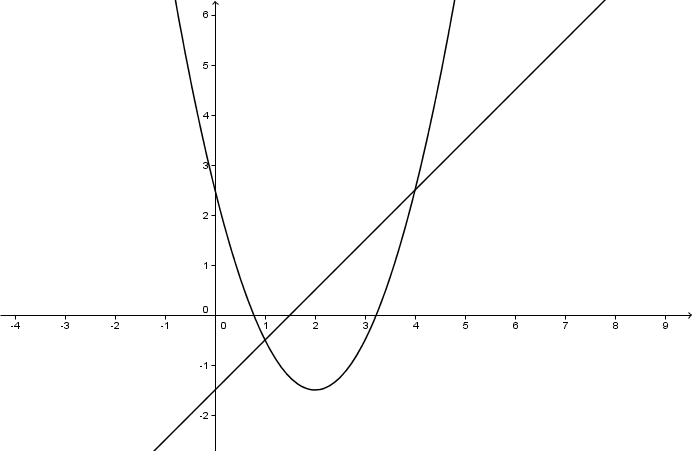
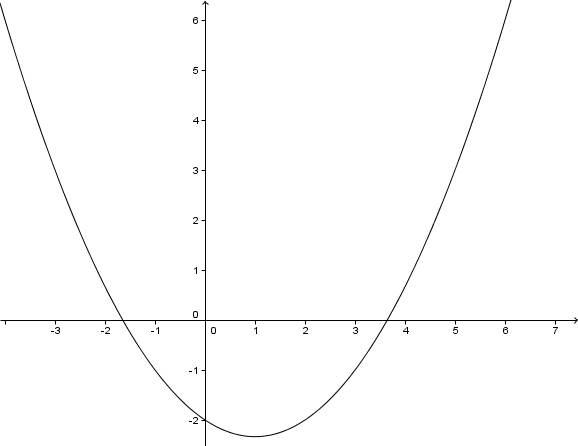
Bestimme die Schnittpunkte der Geraden mit der Parabel rechnerisch.
Kontrolliere dein Ergebnis graphisch.
- 3
Gib jeweils die Gleichung einer Parabel an, die mit der Parabel keinen, einen bzw. zwei verschiedene Schnittpunkte hat.
- 4
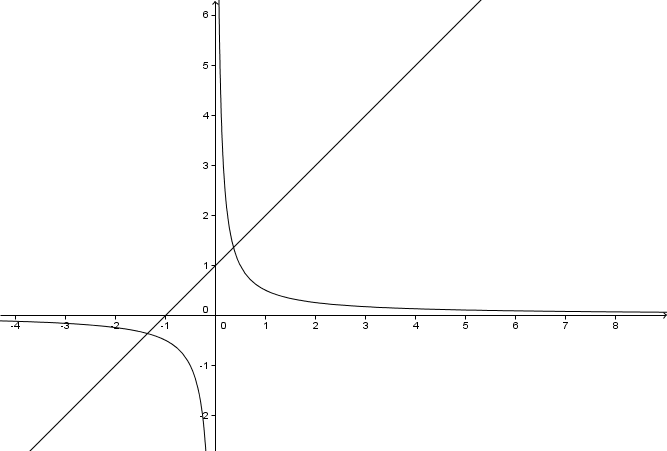
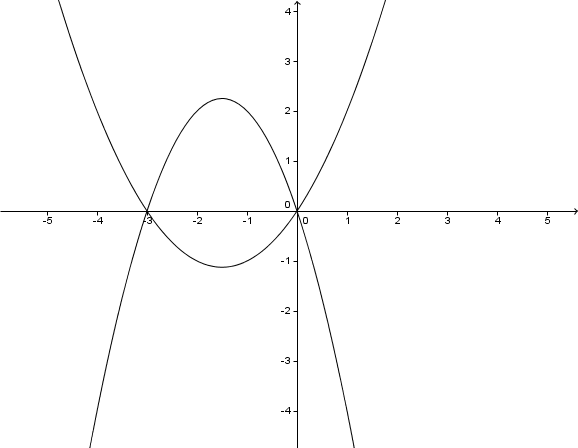
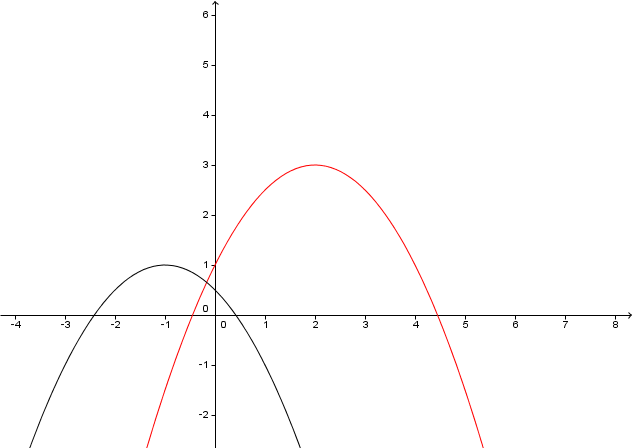
Gegeben sind zwei Funktionen mit den Gleichungen und .
Zeichne die Graphen der beiden Funktionen in ein gemeinsames Koordinatensystem und lies die Koordinaten der Schnittpunkte näherungsweise ab.
Bestimme die Koordinaten der Schnittpunkte exakt.
- 5
Bestimme jeweils die maximale Definitionsmenge und untersuche, ob die Terme und äquivalent sind.
- 6
Berechne für folgende Parabel die Scheitelpunktform und den Scheitelpunkt. Zeichne den Graphen.
- 7
Berechne für folgende Parabeln die Nullstellen, den Scheitelpunkt mithilfe der quadratischen Ergänzung und die Achsenschnittpunkte. Zeichnen Sie den Graphen unter zu Hilfenahme des Scheitelpunkts.
- 8
Welche Bedingungen müssen für die Koeffizienten der Funktion erfüllt sein, damit keine Nullstellen besitzt?
- 9
Untersuche die gegenseitige Lage von und in Abhängigkeit von , wenn gilt:
und
- 10
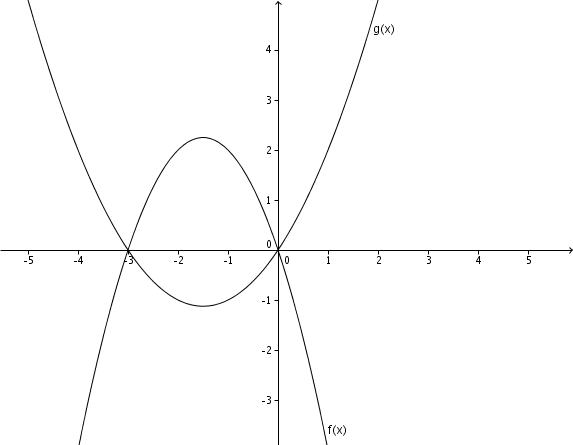
Gegeben sind die quadratischen Funktionen und mit und
Zeichne die Graphen von und in ein Koordinatensystem. Begründe ohne Rechnung, warum sich und auf der x-Achse schneiden.
ist der Scheitel von .
Gib den Scheitel von an.
Die Gerade schneidet den Graphen von im Punkt und den Graphen von im Punkt . Gib und an.
Für ist die Strecke [PQ] eine Seite eines Rechtecks, das den beiden Parabeln einbeschrieben ist. Bestimme den Inhalt des Rechtecks für und den Umfang in Abhängigkeit von .
Im Bild ist :
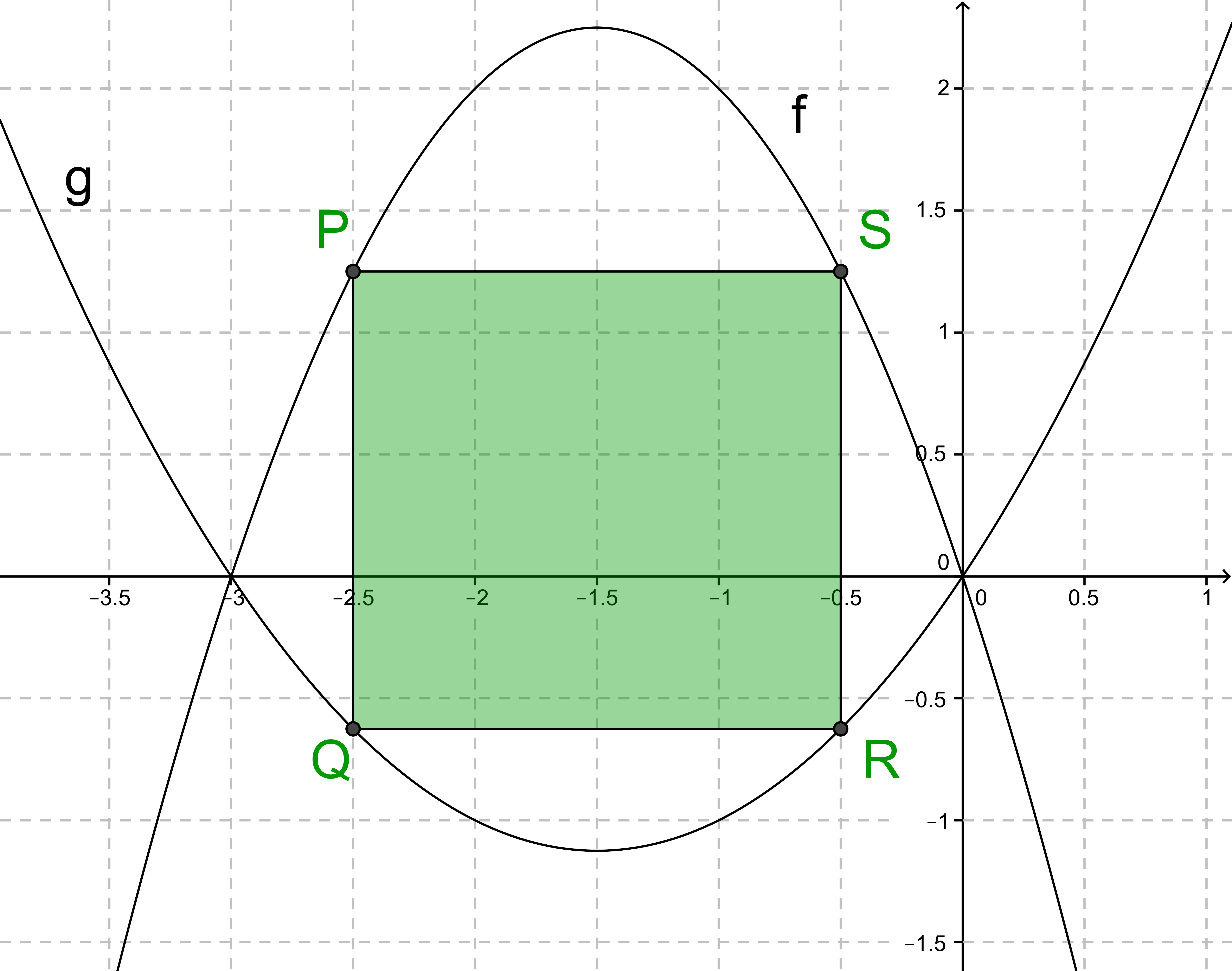
Verschiebe die Parabel in y-Richtung so, dass die verschobene Parabel den Graphen von berührt. Bestimme die Koordinaten des Berührpunktes .
Bestimme so, dass ist.
- 11
Gegeben sind die quadratischen Funktionen und .
Bestimme so, dass der Graph von den Graphen von berührt.
- 12
Zeige, dass es keinen Wert von gibt, sodass der Graph von die Normalparabel berührt.
- 13
Eine Parabel mit der Funktionsgleichung hat ihren Scheitel in und schneidet die x-Achse im Punkt
Bestimme die Funktionsgleichung und zeichne den Graphen.
- 14
Ermitteln Sie die Koeffizienten und so, dass die Funktion an den Stellen und die gleichen Funktionswerte hat wie die Funktion .
- 15
Gegeben sind die Funktionsgleichungen folgender Parabeln.
Bestimme jeweils die Scheitelform und den Scheitelpunkt.
Berechne die Achsenschnittpunkte.
Beschreibe schrittweise, wie aus der Normalparabel durch Verschieben/Strecken entsteht und wie sie geöffnet ist.
Zeichne den Graphen von in ein geeignetes Koordinatensystem.
- 16
Beschreibe, worin sich die Parabeln und unterscheiden, indem du sie in Scheitelpunktsform umwandelst.
- 17
Bestimme die Scheitelform der Parabeln und zeichne sie.
Die Normalparabel wird um 3 gestreckt, um 4 nach rechts und um 1,5 nach unten verschoben. Die Parabel ist nach oben geöffnet.
Die Normalparabel wird um gestaucht, um nach links und um 1 nach unten verschoben. Die Parabel ist nach oben geöffnet.
Die Normalparabel wird um 1.75 gestreckt, um 2 nach links und um 5,25 nach oben verschoben. Die Parabel ist nach unten geöffnet.
- 18
Christian, Manfred und Peter sollten als Hausaufgabe die Gleichung graphisch lösen. Sie sind dabei unterschiedlich vorgegangen, aber alle auf die gleichen Näherungslösungen und gekommen.
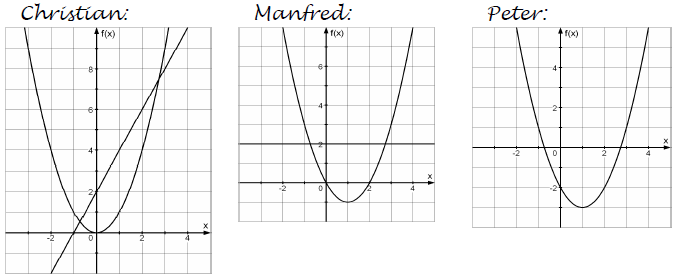
Überprüfe die Näherungslösungen rechnerisch.
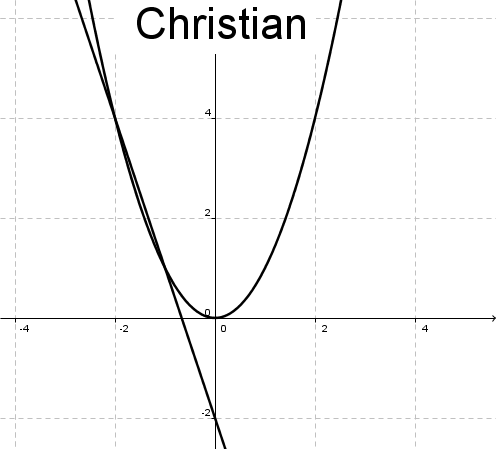
Erläutere die Vorgehensweisen von Christian, Manfred und Peter.
Ermittle mit jedem Verfahren die Lösungen der Gleichung .
Manfred und Peter sind von Christians Methode begeistert und versuchen, damit die Gleichung zu lösen.
Sie gehen dabei aber unterschiedlich vor (siehe nachstehende Abbildungen). Welche Ergebnisse erhalten sie? Überprüfe rechnerisch. Wer von beiden ist deiner Meinung nach geschickter vorgegangen? Begründe.
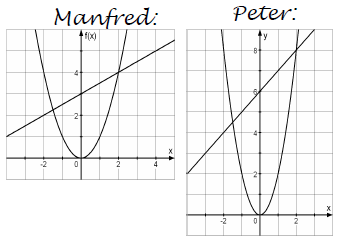
- 19
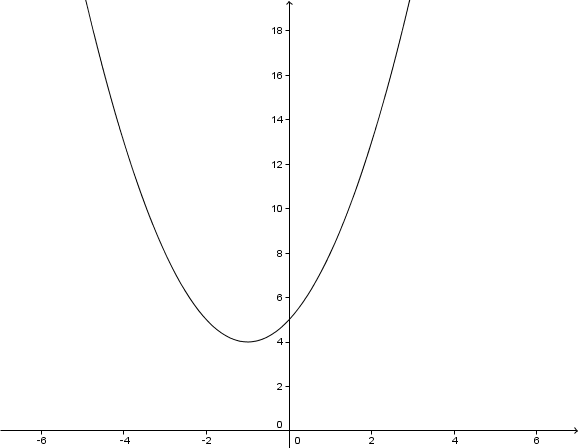
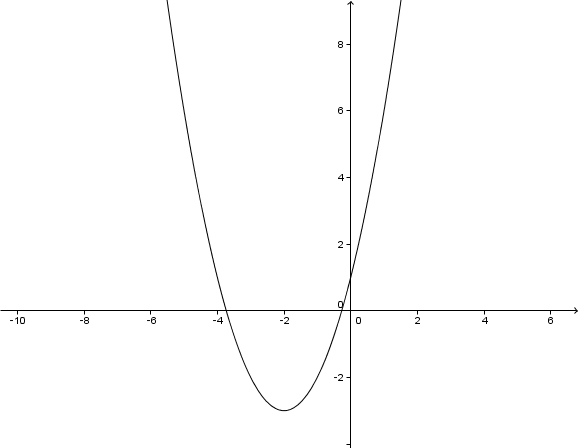
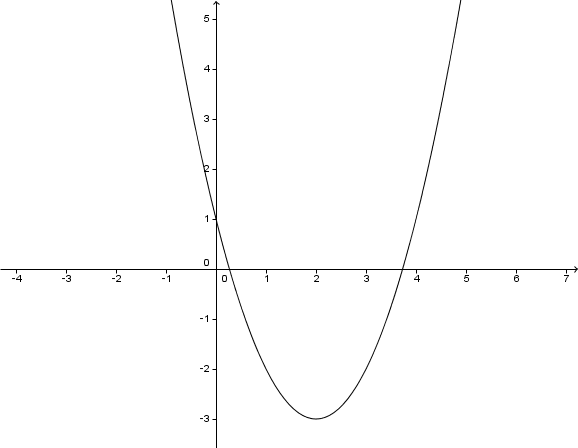
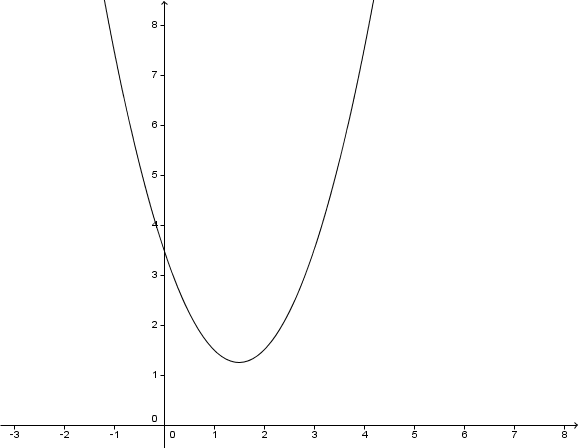
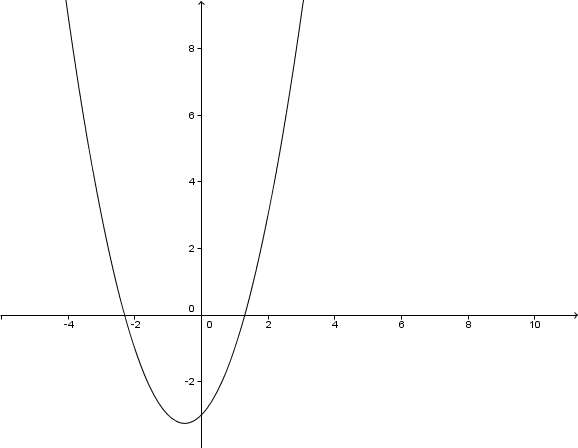
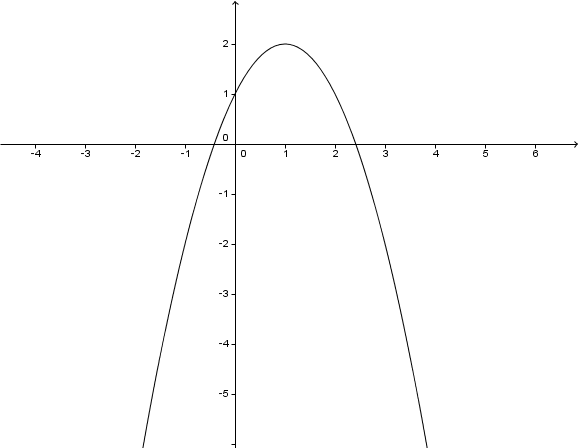
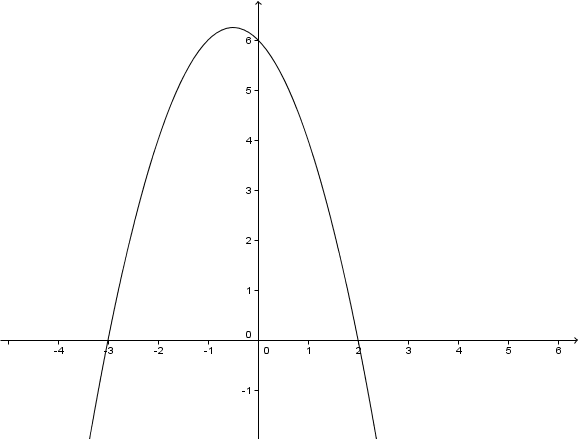
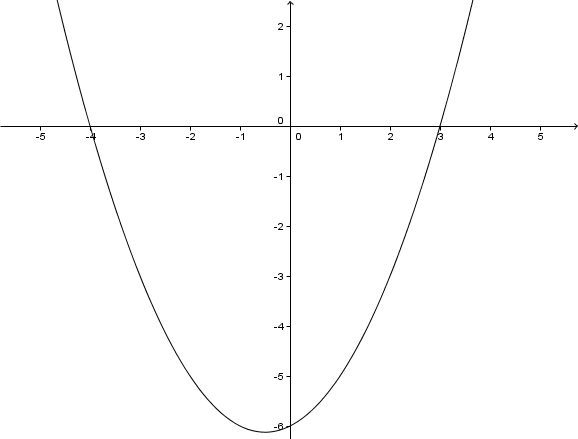
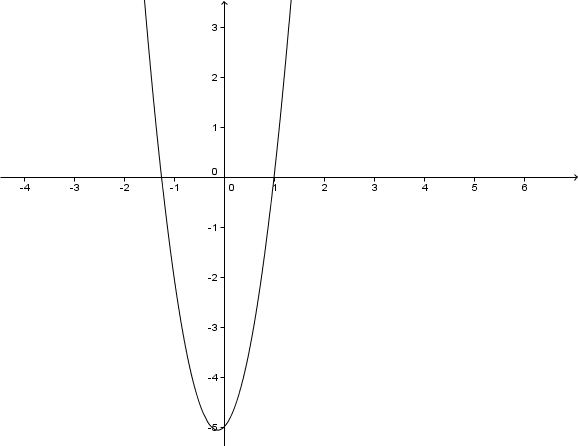
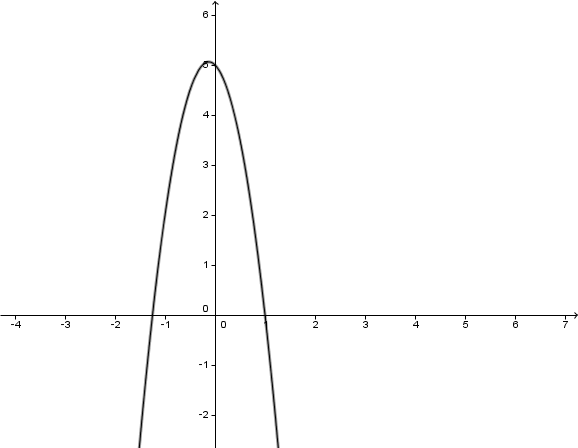
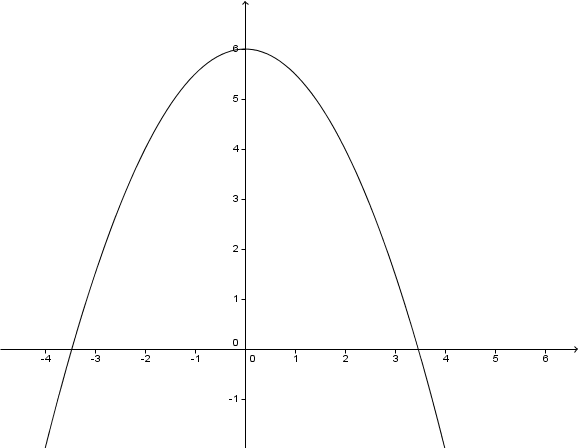
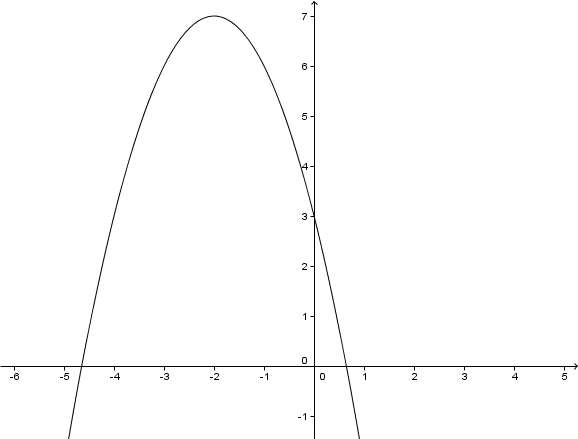
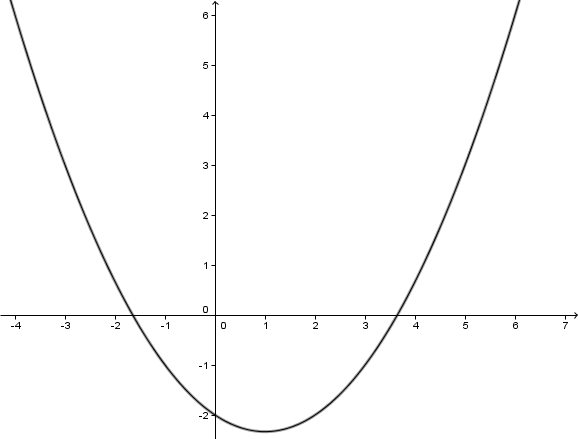
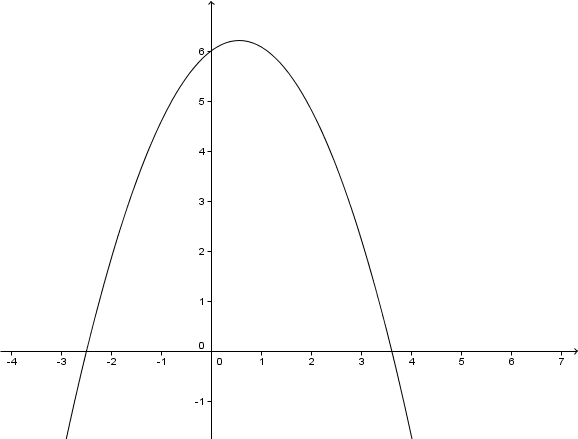
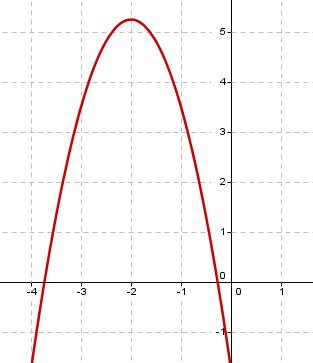
Im folgenden Koordinatensystem ist der Graph einer Parabel abgebildet.
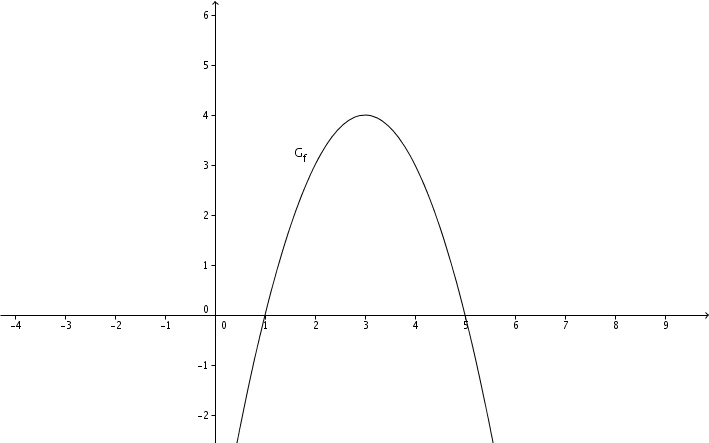
Gib die Funktionsgleichung der abgebildeten Parabel an.
Stelle dir vor, dass sich die Parabel in einem beliebig großen Koordinatensystem beliebig fortsetzt. Was ist dann die Definitionsmenge obiger Funktion?
Angenommen, wir hätten zum Zeichnen des Graphen eine (beliebig große) Wertetabelle berechnet: Welches wird mit Sicherheit der größte y – Wert in dieser Tabelle sein?
Markiere im Graphen die Nullstellen und gib diese an.
Gib nun die Wertemenge der Funktion an.
Setze die beiden in c) ermittelten Nullstellen in die Funktionsgleichung ein und bestätige durch Rechnung, dass es tatsächlich Nullstellen sind.
- 20
Bei welcher der Folgenden Funktionen handelt es sich um quadratische Funktionen?
- 21
Gegeben ist die Funktionsgleichung einer Parabel mit: .
Berechne den Scheitelpunkt mithilfe der Scheitelform.
Berechne die Achsenschnittpunkte.
Die Parabel soll so verschoben werden, dass der Punkt der Parabel, der auf der y-Achse liegt, durch den Punkt verläuft. Wie lautet die Funktionsgleichung der verschobenen Parabel?
Wo schneiden sich beide Parabeln?
Zeichne beide Parabeln in ein geeignetes Koordinatensystem.
- 22
Gegeben ist die Funktionsgleichung einer Parabel mit: .
Berechne den Scheitelpunkt mit Hilfe der Scheitelform.
Berechne die Achsenschnittpunkte.
Die Parabel soll so verschoben werden, dass der Punkt der Parabel, der auf der y-Achse liegt durch den Punkt P (-3| -1) verläuft. Wie lautet die Funktionsgleichung g(x) der verschobenen Parabel?
Wo schneiden sich beide Parabeln?
Zeichne beide Parabeln in ein geeignetes Koordinatensystem.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?