1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, Bruchterme so umzuformen, dass sich das anschließende Ableiten vereinfacht.
Vorkenntnisse

Kursdauer
~ 90 Minuten
2 Eine "komplizierte" Aufgabe (1/2)


3 Eine "komplizierte" Aufgabe (2/2)


Sarah hat den Bruchterm gut zusammengefasst und sich somit das Ableiten einfach gemacht. Sie hat sich ihre 1 wirklich verdient.
4 Bruchterme
Auf der letzten Kursseite war von Bruchtermen die Rede. Aber was ist das eigentlich?
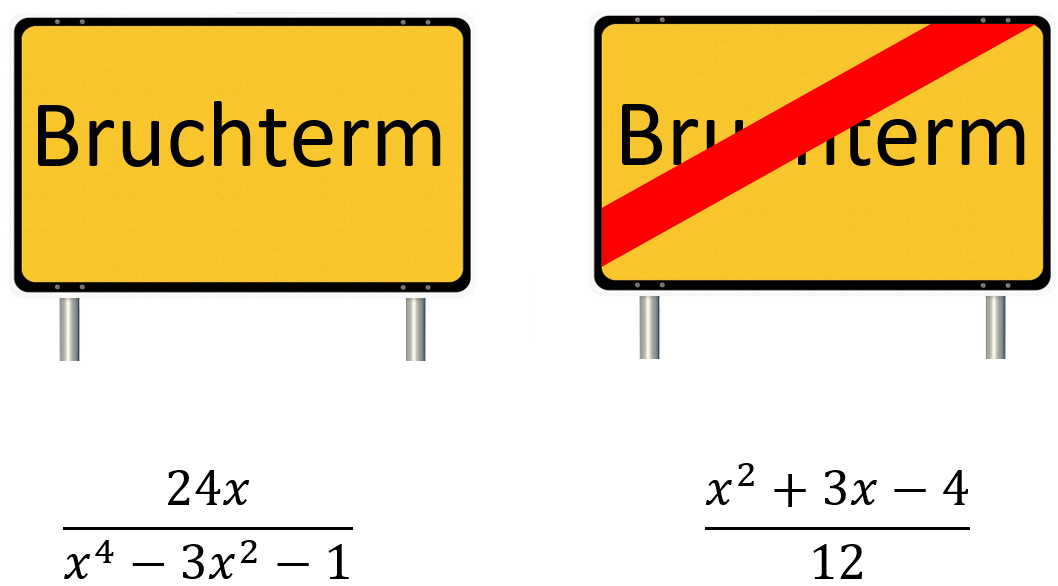
Ein Bruchterm ist ein Term, der aus einem oder mehreren Brüchen besteht und mindestens einmal die Variable im Nenner enthält.
Brüche, bei denen die Variable ausschließlich im Zähler vorkommt, sind streng genommen keine Bruchterme, sondern nur Brüche.
Trotzdem werden im Folgenden auch solche Terme behandelt, da sich die Umformungsmethoden stark ähneln.
Einfaches Ableiten von Bruchtermen
Möchte man solche Bruchterme nun ableiten, dann kann das öfter mal kompliziert aussehen….
Aber keine Sorge! Manchmal sind Brüche oder Bruchterme nicht so kompliziert, wie sie im ersten Augenblick wirken. Wenn man sie geeignet umformt, kann man diese Terme oft einfach ableiten.
Kennst du schon die Quotientenregel? Mit Hilfe dieser kannst du alle Bruchterme erfolgreich ableiten.
Diese Regel interessiert uns vorerst jedoch nicht, denn hier geht es darum, Bruchterme auf möglichst einfache Weise abzuleiten.
5 Umformungen (1/2)
Es gibt verschiedene Methoden zum Umformen von Bruchtermen, die das Ableiten vereinfachen. Im folgenden Abschnitt werden einige zielführende Möglichkeiten vorgestellt.
Erweitern/Kürzen
Erweitern/Kürzen heißt, den Zähler und den Nenner eines Bruchs mit dem gleichen Faktor zu multiplizieren (Erweitern) bzw. durch den gleichen Faktor zu dividieren (Kürzen). Dabei ändert sich der Wert des Bruchs nicht.
Zum Beispiel:
Hier wurde mit erweitert.
Hier wurde mit gekürzt.
Auf einen gemeinsamen Nenner bringen
"Auf einen gemeinsamen Nenner bringen" bedeutet, zwei oder mehrere Brüche so zu erweitern oder zu kürzen, dass sie den gleichen Nenner besitzen. Diese Technik verwendest du beim Addieren und Subtrahieren von Brüchen.

Mathematik findet man auch oft in unserer Alltagssprache wieder.
Zum Beispiel:
Wenn du von den Bruch subtrahierst, dann musst du zuerst einen gemeinsamen Nenner der beiden Brüche finden und sie entsprechend erweitern.Ein gemeinsamer Nenner ist beispielsweise .
| ↓ Erweitere mit . | ||
| ↓ Schreibe die zwei Brüche auf einen Bruchstrich. | ||
| ↓ Fasse den Zähler zusammen. | ||
| ↓ Kürze mit | ||
6 Umformungen (2/2)
Ausklammern
Ausklammern ist die Umkehrung vom Ausmultiplizieren. Man zieht aus zwei oder mehreren Summanden einen gemeinsamen Faktor heraus.
Zum Beispiel:
Binomische Formeln
Die binomischen Formeln lauten:
Die 1. binomische Formel:
Die 2. binomische Formel:
Die 3. binomische Formel:
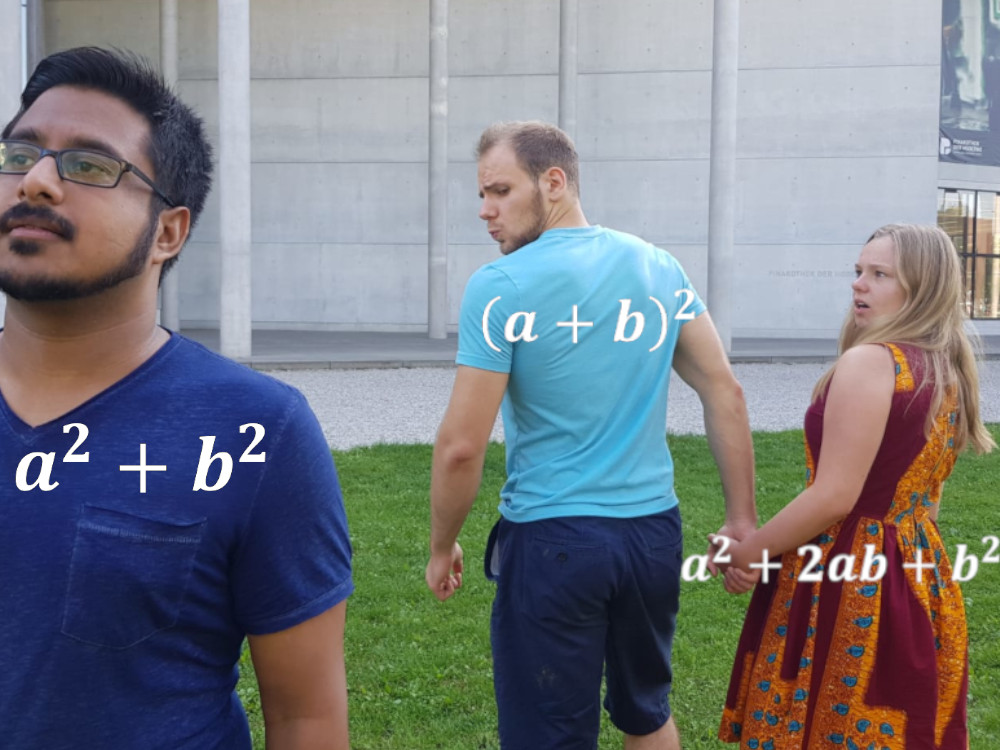
Bleib treu:
Zum Beispiel:
Hier wurde die 3. binomische Formel angewandt und im Anschluss gekürzt.
7 Übungsaufgaben
Laden
Laden
Laden
8 Überleitung
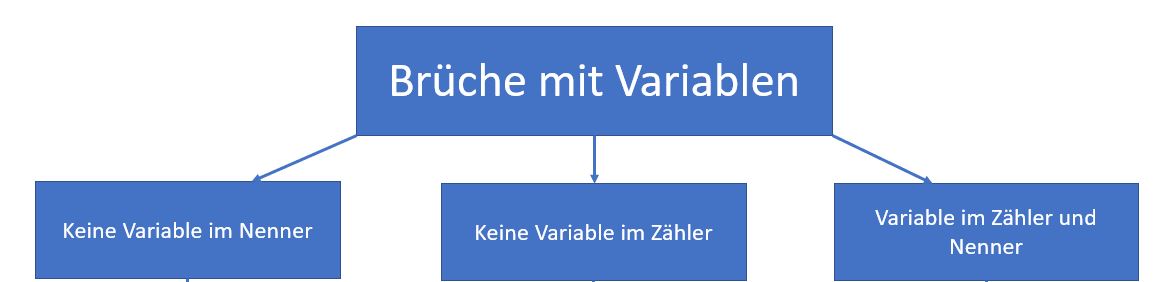
Die drei möglichen Fälle
Wendest du nun die Umformungsmöglichkeiten auf Brüche bzw. Bruchterme an, so erhältst du verschiedene Fälle. Diese werden unterschieden, je nachdem wo die Variable im Bruch auftaucht. Es gibt drei Fälle, die in der folgenden Graphik dargestellt werden.
Ableitung von Potenzfunktionen
Auf den nächsten Kursseiten werden die drei Fälle nacheinander einzeln behandelt. Dabei wird die Regel zum Ableiten von Potenzfunktionen eine wichtige Rolle spielen:
Eine Potenzfunktion leitet man allgemein so ab:
Auch die Faktorregel, die Kettenregel sowie die Produktregel können auf den folgenden Kursseiten beim Ableiten hilfreich sein.
9 Brüche ohne Variable im Nenner
Als Erstes werden nun Brüche ohne Variable im Nenner genauer unter die Lupe genommen. Wie du bereits in den vorherigen Kursseiten gelernt hast, spricht man bei Brüchen ohne Variable im Nenner nicht von einem Bruchterm.
Das Umformen solcher Brüche kann dir einige Vorteile verschaffen, sodass du dir das Ableiten vereinfachen kannst.
Dabei kann es oft besonders nützlich sein, einen Faktor vor den Bruch zu ziehen.
Im Folgenden wird dies allgemein an einem Bruch, welcher ein Polynom zweiten Grades im Zähler hat, formuliert:
für alle und
Dieses Vorgehen kannst du nicht nur für Polynome zweiten Grades im Zähler anwenden, sondern auch für Zählerpolynome n-ten Grades.
10 Beispiele
Beispiel 1
| ↓ | Ziehe den Faktor vor den Bruch. | ||
Bilde nun die Ableitung mit der Faktorregel und Regel zum Ableiten von Potenzfunktionen:
| ↓ | Kürze mit dem Faktor 3. | ||
Die gesuchte Funktion ist also
Beispiel 2
| ↓ | Ziehe den Faktor vor den Bruch. | ||
Bilde nun die Ableitung mit der Faktorregel und Regel zum Ableiten von Potenzfunktionen:
| ↓ | Multipliziere die Klammer aus. | ||
| ↓ | Kürze mit dem Faktor 2. | ||
Die gesuchte Funktion ist also .
11 Übungsaufgaben
Laden
12 Brüche ohne Variable im Zähler
Du benötigst das Potenzgesetz zu negativen Exponenten, das wie folgt lautet:
für wobei
Wenn du die Terme mit diesem Gesetz umgeformt hast, kannst du die Regel zum Ableiten von Potenzfunktionen verwenden.
13 Beispiele
Beispiel 1
| ↓ | Wende das Potenzgesetz zu negativen Exponenten auf die im Nenner an. | ||
Bilde nun die Ableitung mit der Faktorregel und der Regel zum Ableiten der Potenzfunktion:
| ↓ | Verechne die Faktoren vor . | ||
| ↓ | Wende das Potenzgesetz zu negativen Exponenten auf an. | ||
Die Ableitung von ist also .
Beispiel 2
| ↓ | Schreibe den Bruch als Produkt zweier Brüche. | ||
| ↓ | Wende das Potenzgesetz zu negativen Exponenten auf die an. | ||
Bilde nun die Ableitung mit der Faktorregel und der Regel zum Ableiten der Potenzfunktion:
| ↓ | Kürze den Faktor . | ||
| ↓ | Wende das Potenzgesetz zu negativen Exponenten auf an. | ||
Die Ableitung von ist also .
14 Übungsaufgaben
Laden
15 Brüche mit Variable im Zähler und Nenner
Der letzte Abschnitt behandelt nun Funktionen mit Bruchtermen, die auch nach dem Vereinfachen noch Variablen im Zähler und Nenner enthalten.
Solche Bruchterme kannst du auf zwei Arten ableiten:
1. Produkt- und Kettenregel
Wenn du diese Variante wählst, musst du zuerst das Potenzgesetz zu negativen Exponenten anwenden. Danach kannst du mit der Produktregel und der Kettenregel ableiten.
Für eine Funktion bestimmst du die Ableitung mit dieser Methode wie folgt:
| ↓ | Wende das Potenzgesetz zu negativen Exponenten an. | ||
Diese Funktion kannst du nun mit der Produktregel und der Kettenregel ableiten.
2. Quotientenregel
Die Quotientenregel kannst du ohne vorherige Umformung anwenden.
Für eine Funktion bestimmst du die Ableitung mit der Quotientenregel wie folgt:
16 Beispiel (1/2)
Leite einmal mit Produktregel und Kettenregel und einmal mit Quotientenregel ab.
Lösungsvariante 1: mit Produkt- und Kettenregel
Bilde die Ableitung mit der Produktenregel und der Kettenregel.
Ursprungsfunktion:
Zähler der Ursprungsfunktion:
Ableitung des Zählers:
Nenner der Ursprungsfunktion:
Ableitung des Nenners:
| ↓ | Wende das Potenzgesetz zu negativen Exponenten an. | ||
Bilde nun mit Hilfe der Produktregel und der Kettenregel die Ableitung von .
| ↓ | Setze ein. | ||
| ↓ | Wende das Potenzgesetz zu negativen Exponenten an. | ||
| ↓ | Kürze den 2. Bruch mit dem Faktor 2. | ||
| ↓ | Bringe die Brüche auf einen gemeinsamen Nenner. | ||
| ↓ | Addiere die Brüche. | ||
| ↓ | |||
| ↓ | Fasse den Zähler zusammen. | ||
Die Ableitung von ist .
17 Beispiel (2/2)
Lösungsvariante 2: Quotientenregel
Bilde die Ableitung mit der Quotientenregel.
Ursprungsfunktion:
Zähler der Ursprungsfunktion:
Ableitung des Zählers:
Nenner der Ursprungsfunktion:
Ableitung des Nenners:
Bilde nun die Ableitung von , indem du deine Ergebnisse in die Quotientenregel einsetzt.
Die Ableitung von ist also .
18 Übungsaufgabe
Laden
19 Kombinierte Aufgaben
Auf dieser Seite findest du gemischte Aufgaben, die dir helfen, die Umformungen mit den Ableitungen zu kombinieren.
Diese Aufgabensammlung ist so angelegt, dass du am Besten 2-3 Teilaufgaben aus verschiedenen Aufgaben bearbeitest.
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Leite die folgenden Funktionen ab und entscheide welche der abgebildeten Graphen dem Funktionsgrahen der Ableitung der Funktion entsprechen. Fülle in den Feldern dafür den Funktionsnamen ( oder ) ein.
Achtung: Die Graphen entsprechen der Ableitung der Funktion, nicht der Funktion selber.
Laden
Laden
Laden
20 Zusatzwissen: Bilden von Stammfunktionen
Alle Umformungsmethoden für Brüche, die du in diesem Kurs gelernt hast, können dir nicht nur das Ableiten, sondern auch das Bilden von Stammfunktionen erleichtern.
In der nebenstehen Abbildung siehst du, wie Funktion, Stammfunktion und Ableitung zusammenhängen: Durch Ableiten einer Stammfunktion erhältst du die ursprüngliche Funktion . Leitest du diese ebenfalls ab, bekommst du die erste Ableitung . Das Bilden von Stammfunktionen ist der umgekehrte Weg.

Zum Beispiel:
Bilde eine Stammfunktion von .
Vereinfache den Funktionsterm zuerst und bilde dann eine Stammfunktion.
Vereinfachen des Funktionsterms
| ↓ | Wende das Potenzgesetz für negative Exponenten an. | ||
| ↓ | Vereinfache die Exponeten. | ||
Bilden einer Stammfunktion
Verwende die Regel für die Bildung einer Stammfunktion von Potenzfunktionen.
mit | |||
| ↓ | |||
| ↓ | Vereinfache den Term. | ||
Eine Stammfunktion von ist mit .
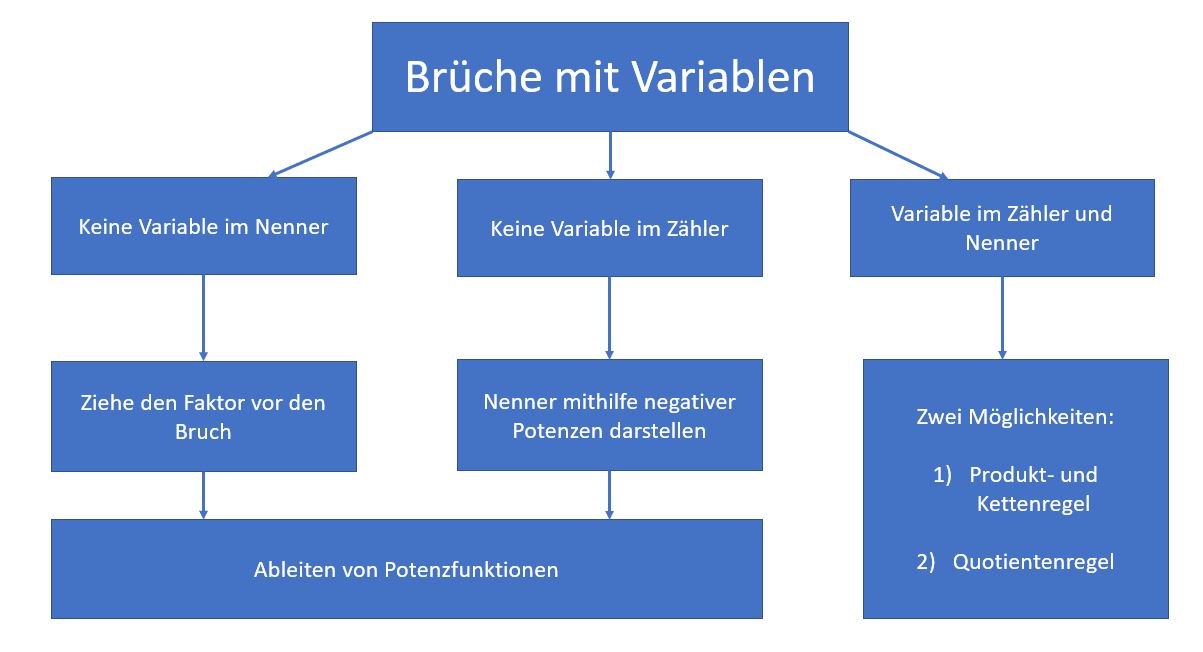
21 Zusammenfassung
Wie bereits in der Überleitung dieses Kurses gesehen, gibt es bei Brüchen mit Variablen drei Möglichkeiten für das Vorkommen von Variablen. Für alle drei Möglichkeiten hast du bereits erfahren, wie du vorgehen kannst.
Die folgende Grafik fasst dir das Vorgehen noch einmal kurz zusammen:
Übrigens: Einen ähnlichen Kurs haben wir auch zum Ableiten von Wurzelfunktionen.

