Aufgaben zur Diskussion von e-Funktionen

1
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Gegeben sind die Funktionen $f$ und $g$ mit $f\left(x\right)=1+e^{1-x}$ und $g\left(x\right)=2\cdot e^{x-1}$ .
1. Skizziere die beiden Graphen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Video: Funktionsgraphen der Exponentialfunktionen
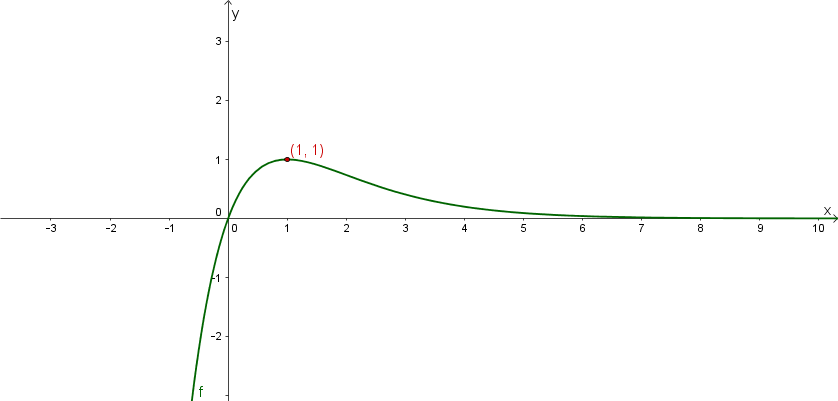
  Graphen der Funktionen f und g
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme den Schnittpunkt der beiden Graphen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkten zweier Graphen
  Du suchst nach Werten $x$ , die
  in den Definitionsmengen $D_{f}$ und $D_{g}$ beider Funktionen $f$ und $g$ enthalten sind und
  $f(x) = g(x)$ erfüllen.
  Um solche Werte $x$ zu finden, löst du die Gleichung $f(x) = g(x)$ nach $x$ auf, falls dies möglich ist.
  $f(x)=g(x)$
  In diese Gleichung setzt du die Definitionsgleichungen $f(x)=1+\mathrm e^{1-x}$ und $g(x)=2\mathrm e^{x-1}$ von $f$ und $g$ ein.
  $\Leftrightarrow 1+\mathrm e^{1-x} = 2\mathrm e^{x-1}$
  Nun kannst du $x-1$ durch $-(1-x)$ ersetzen.
  $\Leftrightarrow 1+\mathrm e^{1-x} = 2\mathrm e^{-(1-x)}$
  Anschließend kannst du beide Seiten der Gleichung mit $\mathrm e^{1-x}$ multiplizieren, um die rechte Seite der Gleichung zu vereinfachen: Dabei ist aufgrund der Potenzgesetze $\mathrm e^{1-x} \cdot\mathrm e^{-(1-x)} = \mathrm e^0 = 1$ .
  $\Leftrightarrow\mathrm e^{1-x} + (\mathrm e^{1-x})^2 = 2$
  Vertausche die Summanden (Kommutativgesetz der Addition).
  $\Leftrightarrow (\mathrm e^{1-x})^2 + \mathrm e^{1-x} = 2$
  Dies erinnert an eine quadratische Gleichung. Nun kannst du mit $y = \mathrm e^{1-x}$ eine Substitution durchführen, d. h., du betrachtest eine veränderte Gleichung, in der du den komplizierteren Ausdruck $\mathrm e^{1-x}$ durch $y$ ersetzt; dies liefert eine einfacher aussehende Gleichung:
  $y^2 + y = 2$
  Hier kannst du $2$ auf die linke Seite der Gleichung bringen.
  $\Leftrightarrow y^2 + y - 2 = 0$
  Nun hast du eine quadratische Gleichung erhalten, die der Theorie gemäß höchstens zwei reelle Lösungen (d. h. Nullstellen) hat. Diese kannst du mit der $pq$ -Formel berechnen:
  $\Leftrightarrow y \in \{-2, 1\}$
  (Hier gilt der Äquivalenzpfeil, da die Gleichung genau zwei reelle Lösungen hat.)
  Die Exponentialfunktion $\operatorname{exp}\colon \mathbb{R} \rightarrow \mathbb{R}^+, x \mapsto\mathrm e^x$ nimmt nur positive Werte an. Deswegen kann auch $\mathrm e^{1-x} = \operatorname{exp}(1-x)$ nur positive Werte annehmen und die Gleichung $y = \mathrm e^{1-x}$ ist lediglich für $y = 1$ erfüllbar.
  $\mathrm e^{1-x} = 1$
  Wie du vielleicht schon weißt, ist $\operatorname{exp}(0) = \mathrm e^0 = 1$ . Also ist $x = 1$ eine mögliche Lösung. Durch Anwendung der natürlichen Logarithmusfunktion $\operatorname{ln}$ auf beide Seiten der Gleichung erhältst du
  $\Leftrightarrow \operatorname{ln}(\mathrm e^{1-x}) = \operatorname{ln}(1)$
  Da $\operatorname{ln}$ die Umkehrfunktion von $\operatorname{exp}$ auf ganz $\mathbb{R}$ ist (deswegen bleibt der Äquivalenzpfeil gültig), gilt $\operatorname{ln}(\mathrm e^x) = x$ . Aus dem Artikel zur $\operatorname{ln}$ -Funktion könntest du dir gemerkt haben, dass $\operatorname{ln}(1) = 0$ ist.
  $\Leftrightarrow 1-x = 0$
  Hier kannst du $x$ auf die andere Gleichungsseite bringen und bekommst die gesuchte Lösung der Gleichung $f(x) = g(x)$ .
  $\Leftrightarrow x = 1$
  Als Letztes musst du diesen $x$ -Wert noch in eine der beiden ursprünglichen Funktionen einsetzen, um den $y$ -Wert des Schnittpunkts herauszufinden.
  $f(1)=1+\mathrm e^{1-1}=1+\mathrm e^0=1+1=2$
  Also liegt der gesuchte Schnittpunkt bei $S(1\mid2)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Unter welchem Winkel schneiden sich die beiden Graphen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Geraden
  Berechnung des Schnittwinkels zweier reeller Funktionen in einem Punkt:
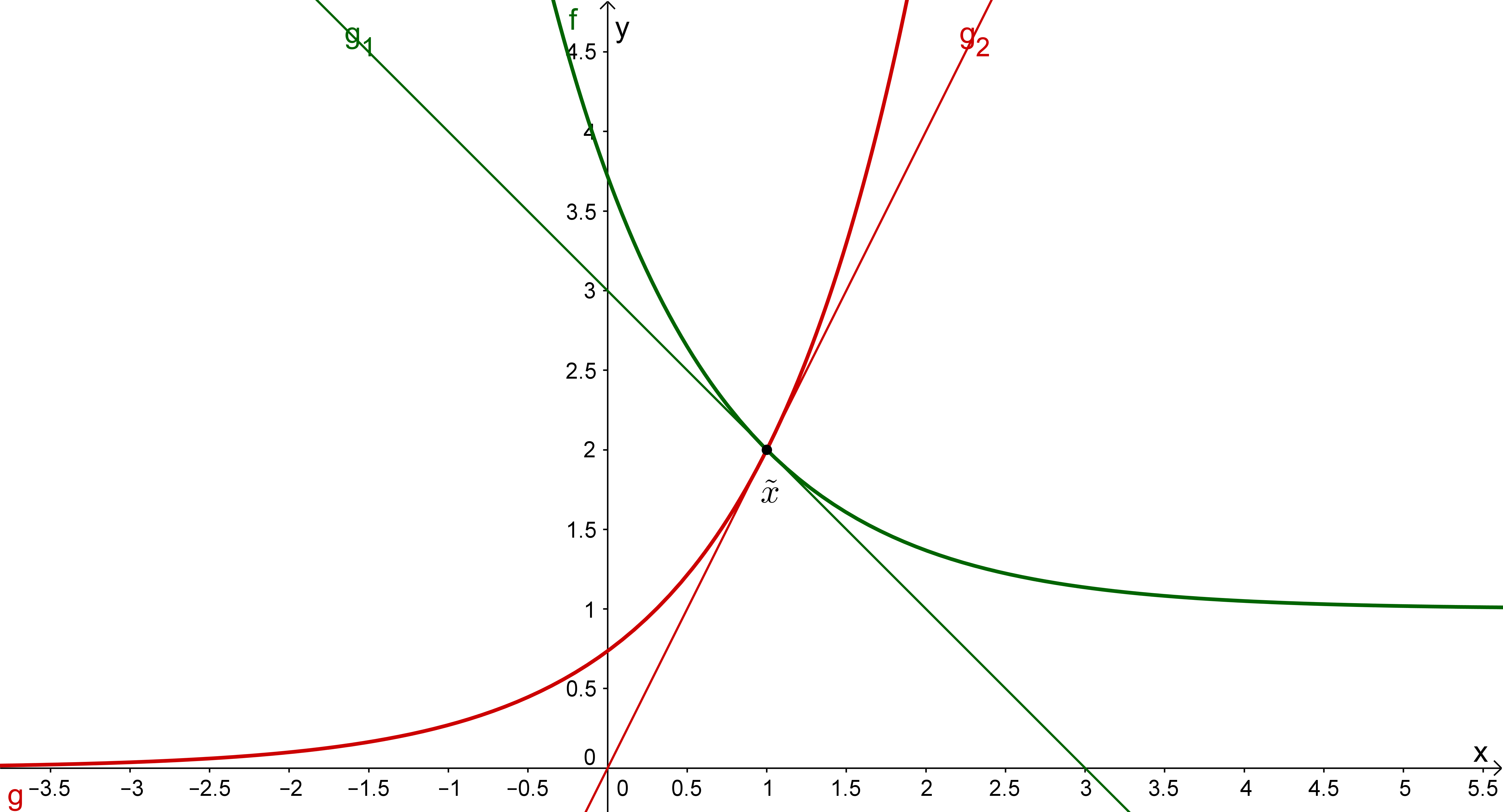
  Gegeben sind zwei Funktionen $f:D_{f} \rightarrow \mathbb{R}$ , $g:D_{g} \rightarrow \mathbb{R}$ , deren Graphen sich in einem Punkt $\tilde x$ gemäß Teilaufgabe b) schneiden: $f(\tilde x) = g(\tilde x)$ . $f$ und $g$ wollen wir als in $\tilde x$ differenzierbar voraussetzen.
  Du kannst nun folgendermaßen vorgehen: Berechne Geraden $g_{1}: y = k_{1} x + d_{1}$ und $g_{2}: y = k_{2} x + d_{2}$ , welche die nachstehenden Eigenschaften aufweisen:
  $f'(\tilde x) = k_{1}$ und $g'(\tilde x) = k_{2}$
  $f(\tilde x) = k_{1} \tilde x + d_{1}$ und $g(\tilde x) = k_{2} \tilde x + d_{2}$
  Dies bedeutet, in Worte gefasst:
  Die Steigung von $g_{1}$ ist gleich der Steigung von $f$ in $\tilde x$ und die Steigung von $g_{2}$ ist gleich der Steigung von $g$ in $\tilde x$ .
  Der Schnittpunkt $(\tilde x, f(\tilde x)) = (\tilde x, g(\tilde x))$ der Graphen von $f$ und $g$ ist in $g_{1}$ und $g_{2}$ enthalten.
  Anschließend kannst du den Schnittwinkel beider Geraden durch deren Richtungsvektoren $\overrightarrow{g_{1}}$ und $\overrightarrow{g_{2}}$ mittels der Formel $cos(\phi)=\frac{\langle\overrightarrow{g_{1}}, \overrightarrow{g_{2}} \rangle}{\lvert \overrightarrow{g_{1}} \rvert \cdot \lvert \overrightarrow{g_{2}} \rvert}$ berechnen ( $\langle ., . \rangle$ bezeichnet das Standardskalarprodukt):
  In Teilaufgabe b) war der Schnittpunkt $\tilde x = 1$ mit $f(1)=g(1)=2$ .Um die Steigungen von $f$ und $g$ in $\tilde x = 1$ zu berechnen, benötigen wir deren Ableitungen an dieser Stelle:
  $f'(x) = -e^{1-x}$ und $g'(x) = 2 \cdot e^{x-1}$ .
  $f'(1) = -e^{1-1} = -e^0 = -1$
  $g'(1) = 2 \cdot e^{1-1} = 2 \cdot e^0 = 2$
  Anschließend kannst du die gesuchten Geraden bestimmen, indem du $k_{1} = f'(1)$ und $k_{2} = g'(1)$ setzt (damit ist 1. erfüllt). Wenn du weiterhin noch 2. forderst, erhältst du durch Einsetzen von $\tilde x = 1, f(1), g(1), k_{1}$ und $k_{2}$ zwei Gleichungen. Diese Gleichungen formst du um, um die fehlenden Werte $d_{1}$ und $d_{2}$ zu berechnen:
  und
  Nach diesen Schritten hast du die Geradengleichungen von $g_{1}$ und $g_{2}$ ermittelt:
  $g_{1}: y = (-1) \cdot x + 3$
  $g_{2}: y = 2 \cdot x$
  (siehe auch: (*) Alternativer Lösungsweg)
  Du kannst sofort die Normalform der Geraden angeben,
  $g_{1}: x + y = 3$
  $g_{2}: (-2) \cdot x + y = 0$
  sowie deren Normalenvektoren $\overrightarrow{n}_{g_{1}}$ und $\overrightarrow{n}_{g_{2}}$ ablesen: $\binom{1}{1}$ und $\binom{-2}{1}$ .
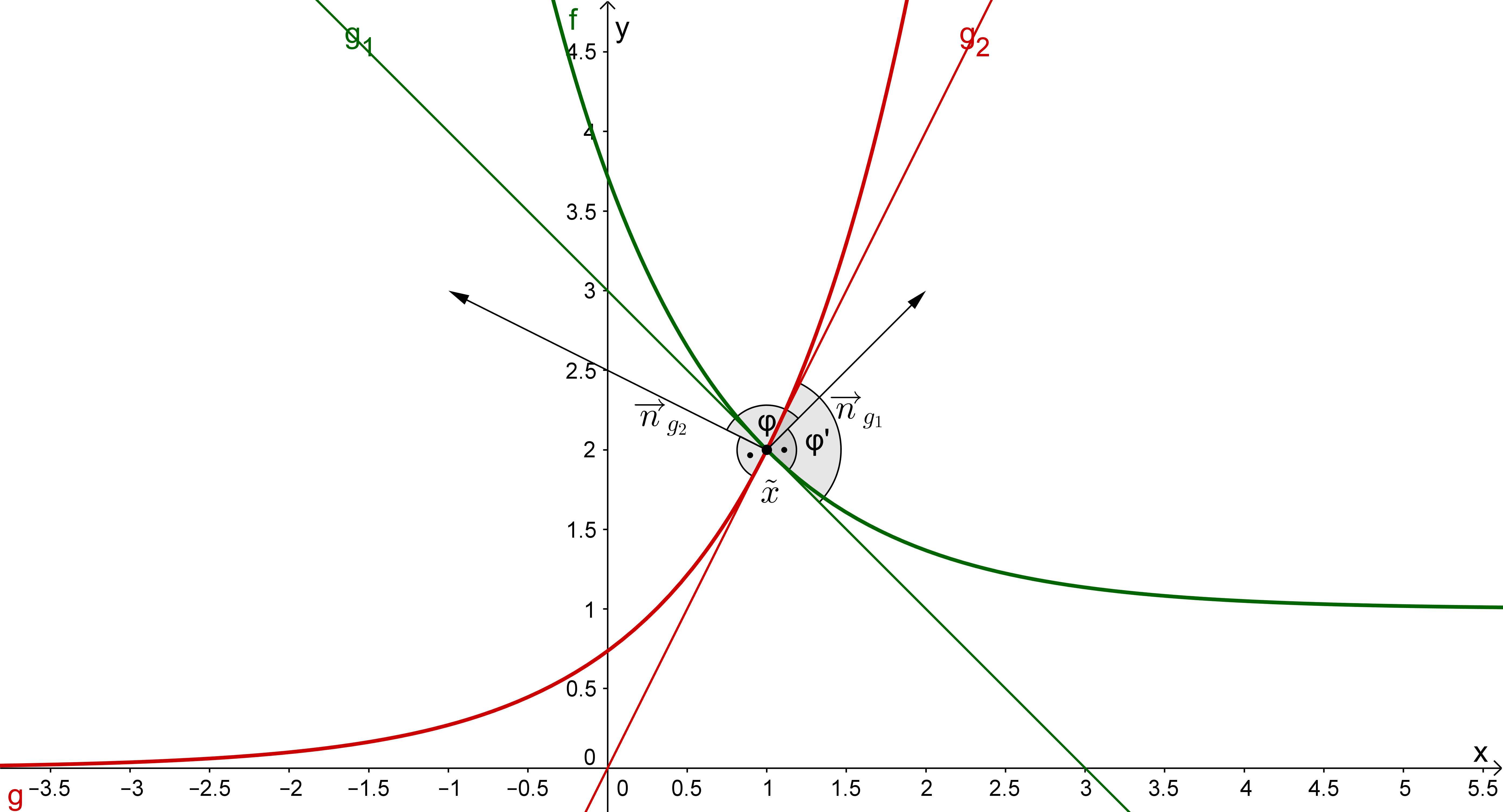
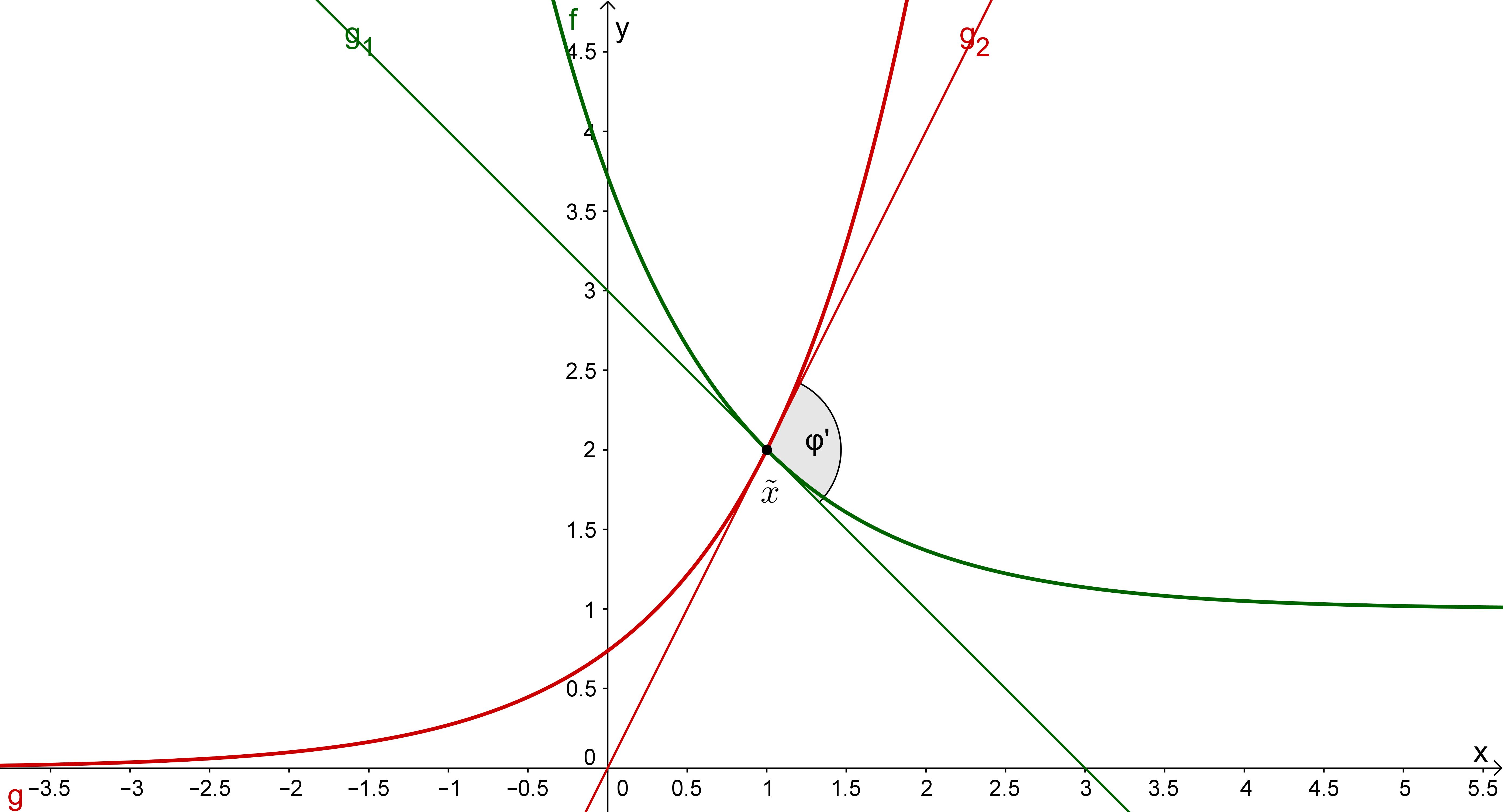
  Da Normalenvektoren in der Ebene senkrecht, d.h. in einem Winkel von $90°$ auf den Richtungsvektor der Geraden stehen, ist in obiger Grafik $\varphi = \varphi'$ . Also kannst du $\phi$ mit der weiter oben angegebenen Formel berechnen, wobei du jedoch nicht die Richtungs-, sondern die Normalenvektoren verwendest:
  $\def\arraystretch{1.25} \begin{aligned}\Rightarrow \varphi &= cos^{-1}(-\frac{1}{\sqrt{10}})\\&\approx 108{,}4°\end{aligned}$
  Unter Verwendung eines Taschenrechners ist es dir möglich, den Wert von $cos^{-1}(-\frac{1}{\sqrt{10}})$ (in $°$ Winkelmaß) zu berechnen.
  Achtung: Versichere dich davor in dessen Einstellungsmenü davon, dass du dein Ergebnis nicht in $°$ Radiant angegeben erhältst.
  (*) Alternativer Lösungsweg
  Dieser Lösungsweg verwendet keine Vektoren, sondern benutzt die Tatsache, dass die Steigung m einer Gerade durch $m=\tan\left(\alpha\right)$ gegeben ist. Auflösen nach dem Steigungswinkel $\alpha$ (=Winkel gegen die Horizontale) durch Anwenden von $\tan^{-1}\left(..\right)$ auf beiden Seiten der Gleichung liefert:
  Wir hatten:
  $g_{1}: y = - x + 3 \;$ mit Steigung $\;m_1=-1$ .
  $g_{2}: y = 2 \cdot x\;$ mit Steigung $\;m_2=2$
  Berechne nun den Steigungswinkel gemäß der Formel von oben.
  Steigungswinkel von $g_1$ : $\alpha_1=\tan^{-1}\left(m_1\right)=\tan^{-1}\left(-1\right)=-45^\circ$
  Steigungswinkel von $g_2$ : $\alpha_2=\tan^{-1}\left(m_2\right)=\tan^{-1}\left(2\right)\approx63{,}4^\circ$
  Berechne den Schnittwinkel. Ziehe dazu die Winkel voneinander ab und bilde deren Betrag.
  $\varphi=\left|\alpha_2-\alpha_1\right|\approx\left|63{,}4^\circ-(-45^\circ)\right|=108{,}4^\circ$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Gegeben ist die Funktion $f$ mit $f\left(x\right)=x\cdot e^{1-x}$ .
1. In welchen Intervallen ist $f$ streng monoton wachsend?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten einer reellwertigen Funktion bestimmen
  Eine reellwertige Funktion $f\colon[a,b] \rightarrow \mathbb{R}$ auf einem Intervall $[a,b]$ mit $a < b$ heißt
  monoton wachsend auf $[a,b]$ , falls aus $a \leq x \leq y \leq b$ folgt, dass $f(x) \leq f(y)$ ist.
  streng monoton wachsend auf $[a,b]$ , falls aus $a \leq x < y \leq b$ folgt, dass $f(x) < f(y)$ ist.
  Kurz gesagt bedeutet monotones Wachstum: Je weiter du von $a$ ausgehend auf $b$ zugehst, desto größer werden die Funktionswerte von $f$ .
  monoton fallend auf $[a,b]$ , falls aus $a \leq x \leq y \leq b$ folgt, dass $f(x) \geq f(y)$ ist.
  streng monoton wachsend auf $[a,b]$ , falls aus $a \leq x < y \leq b$ folgt, dass $f(x) < f(y)$ ist.
  Kurz gesagt bedeutet monotone Abnahme: Je weiter du von $a$ ausgehend auf $b$ zugehst, desto kleiner werden die Funktionswerte von $f$ .
  Ist die betrachtete Funktion $f\colon[a,b] \rightarrow \mathbb{R}$ differenzierbar, so kannst du ihr Monotonieverhalten folgendermaßen bestimmen:
  Ist $f'(x) \geq 0$ (bzw. $>0$ ) für alle $x$ in $[a,b]$ , so wächst $f$ monoton (bzw. streng) auf $[a,b]$ .
  Ist $f'(x) \leq 0$ (bzw. $<0$ ) für alle $x$ in $[a,b]$ , so fällt $f$ monoton (bzw. streng monoton) auf $[a,b]$ .
  Dieses Vorgehen kannst du auf differenzierbare Funktionen $f\colon\mathbb{R} \rightarrow \mathbb{R}$ verallgemeinern, indem du die Ableitung $f'$ berechnest und $\mathbb{R}$ in größtmögliche Intervalle unterteilst, auf welchen $f' \geq 0$ oder $f' \leq 0$ ist.
  In dieser Aufgabe ist
  $f(x)=x \cdot \mathrm e^{1-x}$
  $f$ ist laut Produkt- und Kettenregel differenzierbar, womit du also ihre Ableitung berechnen kannst:
  $f'(x) =$
  Anwendung der Produktregel
  $(x)' \cdot\mathrm e^{1-x} + x \cdot (\mathrm e^{1-x})'=$
  Anwendung der Kettenregel unter Benutzung von $(\mathrm e^x)'=\operatorname{exp}'(x)=\operatorname{exp}(x)=\mathrm e^x$ liefert:
  $(\mathrm e^{1-x})'=$
  $(\mathrm exp(1-x))'=$
  $\operatorname{exp}'(1-x) \cdot (1-x)'=$
  $\operatorname{exp}(1-x) \cdot (-1)=$
  $-\mathrm e^{1-x}$
  Durch Einsetzen der Ableitung $(x)'=1$ erhältst du
  $1 \cdot\mathrm e^{1-x} + x \cdot (-1) \cdot\mathrm e^{1-x}=$
  Hier kannst du den Ausdruck $\mathrm e^{1-x}$ herausheben:
  $(1-x) \cdot\mathrm e^{1-x}$
  Dabei ist $\mathrm e^{1-x}$ für reelle $x$ immer positiv.
  Daher hängt das Vorzeichen von $f'(x)$ nur von dem Ausdruck $1-x$ ab:
  $1-x>0$ für $x<1$ und
  $1-x<0$ für $x>1$ .
  Insgesamt ist
  $f'(x)>0$ für $x<1$ und
  $f'(x)<0$ für $x>1$ .
  Nach dem obigen Kriterium für differenzierbare Funktionen kannst du folgende Aussage zum Monotonieverhalten von $f$ angeben:
  $f$ wächst streng monoton für $x<1$ und fällt streng monoton für $x>1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme alle Hoch- und Tiefpunkte des Graphen von $f$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hoch- und Tiefpunkte berechnen
  Aus Teilaufgabe a) weißt du bereits, dass $f'(x) = (1-x) \cdot e^{1-x}$ ist. Berechne nun die Nullstellen der ersten Ableitung.
  $f'(x) = 0$
  Setze für $f'(x)$ ein.
  $\Leftrightarrow (1-x) \cdot e^{1-x} = 0$
  Desweiteren solltest du aus Teilaufgabe a) in Erinnerung behalten haben, dass $e^{1-x}>0$ ist. Somit ist die linke Seite der Gleichung genau dann gleich Null, wenn $1-x=0$ ist. Dies ist nur für $x=1$ erfüllt.
  $\Leftrightarrow x=1$
  $x=1$ ist also der einzige Punkt von $f$ , der als Hoch- oder Tiefpunkt in Frage kommt.
  Um zu entscheiden, ob es sich um einen Hoch- oder Tiefpunkt handelt, berechnest du die zweite Ableitung von $f$ .
  $f''(x) = ((1-x) \cdot e^{1-x})'$
  Wende die Produktregel an.
  $=(1-x)' \cdot e^{1-x} + (1-x) \cdot (e^{1-x})'$
  Wie in Teilaufgabe a) nutzt du zum Ableiten von $e^{1-x}$ die Kettenregel und erhältst $(e^{1-x})'=-e^{1-x}$ . Dies setzt du zusammen mit $(1-x)'=-1$ ein.
  $=-e^{1-x}+(-1) \cdot (1-x) \cdot e^{1-x}$
  Hineinziehen des Minuszeichens in die Klammer.
  $=-e^{1-x}+(x-1) \cdot e^{1-x}$
  Nun klammerst du $e^{1-x}$ aus.
  $=(-1 + x-1) \cdot e^{1-x}= (x-2) \cdot e^{1-x}$
  Nun setzt du $x=1$ in die 2. Ableitung von $f$ ein.
  
  Da $f''(1)$ kleiner als 0 ist, ist $x=1$ ein Hochpunkt von $f$ .
  Die Funktion $f(x)=x⋅e^{1−x}$ hat genau einen Hochpunkt bei $x=1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne zuerst die Nullstellen der 1. Ableitung.
  Überprüfe mithilfe der 2. Ableitung, ob es sich um Hoch- oder Tiefpunkte handelt.
3. Skizziere den Graphen von $f$ .
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Gegeben ist die Funktion $f$ mit $f(x)=(x^2+x-5)\cdot e^x$ .
Bestimme alle Hoch- und Tiefpunkte des Graphen von $f$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Hoch- und Tiefpunkte berechnen
$f(x) = (x^2 + x - 5) \cdot e^x$
Zum Ableiten von $f(x)$ benötigst du die Produktregel:
Die Ableitung des ersten Faktors $x^2+x-5$ ist:
Damit erhältst du für die gesamte Ableitung
Nun berechnest du die Nullstellen von f(x) , also die Lösung der Gleichung von $f'(x)=0$ :
$f'(x)=0$
$\Leftrightarrow e^x \cdot (x^2 + 3x -4) = 0$
Die linke Gleichungsseite ist genau dann gleich $0$ , wenn einer der beiden Faktoren des dortigen Produktes gleich $0$ ist.
Also $e^x=0$ oder $x^2+3x−4=0$ .
Da die Exponentialfunktion $x \mapsto e^x$ nur positive Werte annimmt, gibt es für $e^x=0$ keine Lösung. Löse also nun $x^2 + 3x -4 = 0$ .
Dies kannst du mit der PQ-Formel berechnen:
$\Rightarrow x_1=-\frac{3}{2} + \frac{5}{2}=1 \\ x_2=-\frac{3}{2} - \frac{5}{2}=-4$
$\Leftrightarrow x \in \{-4, 1\}$
Um nun herauszufinden, ob es sich bei diesen um Hoch- oder Tiefpunkte handelt, musst du sie in die zweite Ableitung von $f$ einsetzen. Dafür berechnest du zuerst $f''(x)$ mit Hilfe der Produktregel:
Nun setzt du die Nullstellen der 1. Ableitung -4 und 1 in die zweite Ableitung ein.
$f''(-4) = ((-4)^2+5 \cdot (-4)-1) \cdot e^{-4} = (16 - 20 - 1) \cdot e^{-4} = -5 \cdot \underbrace {e^{-4}}_{>0} < 0$ ,
sowie
$f''(1) = (1^2+5 \cdot 1-1) \cdot e^{1} = (1 + 5 - 1) \cdot e = 5 \cdot \underbrace {e}_{>0} > 0$ .
Du siehst nun, dass an der Stelle $x=-4$ der Graph von $f$ einen Hochpunkt und an der Stelle $x=1$ einen Tiefpunkt hat.
Im Schaubild unten siehst du den Graphen von $f(x)$ gezeichnet (keine Sorge, dass war in der Aufgabe nicht verlangt ;-) ). Wie du siehst passen Hoch- und Tiefpunkt zum Graphen.
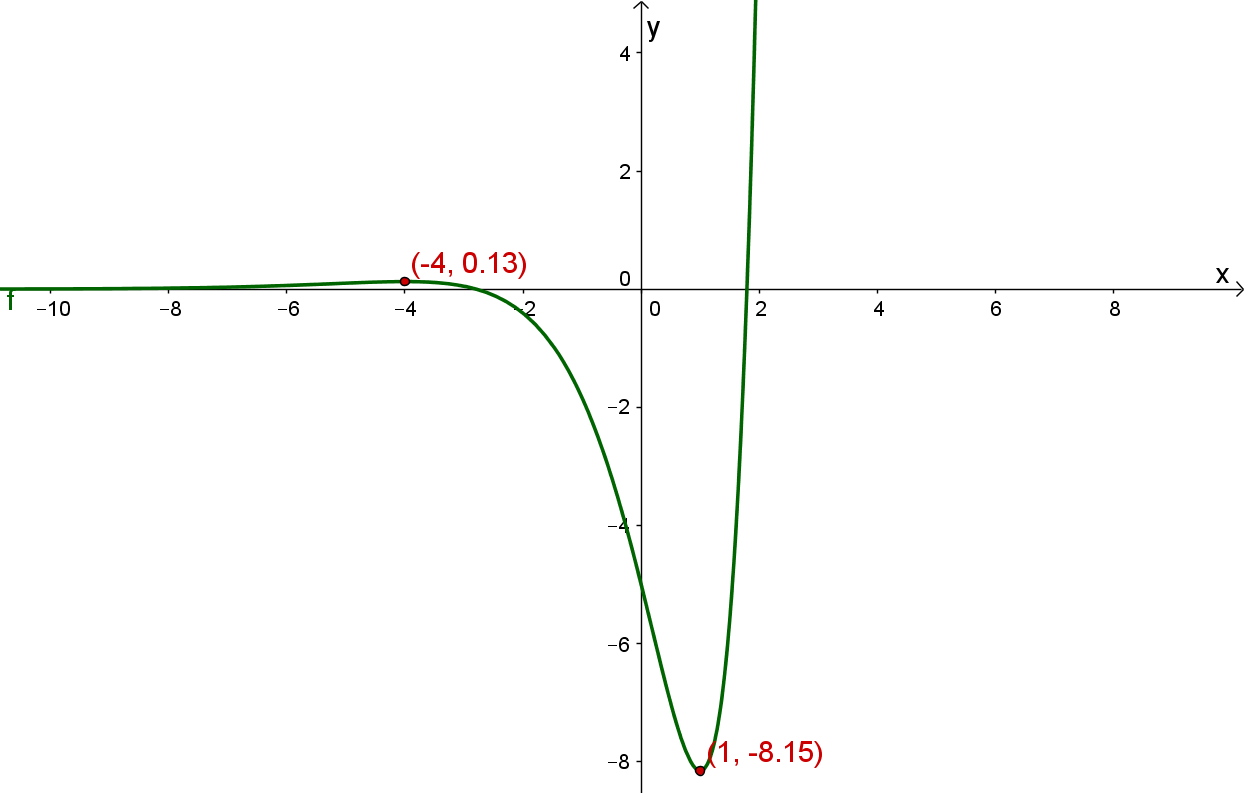
Berechne zuerst die Nullstellen der 1. Ableitung.
Überprüfe mithilfe der 2. Ableitung, ob es sich um Hoch- oder Tiefpunkte handelt.
4
Diskutiere folgende Funktionen so weit, bis du den Graphen zeichnen kannst. Gib gegebenenfalls die Asymptoten an:
1. $f(x)=e\cdot e^x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
  Definitionsbereich festlegen
  Da die Funktion keine Brüche, Wurzeln oder andere Dinge enthält, die den Definitionsbereich einschränken könnten, ist der Definitionsbereich der Funktion $D_f=ℝ$ .
  Nullstellenbestimmung
  Die $e$ -Funktion besitzt keine Nullstelle, weshalb die betrachtete Funktion $f$ ebenfalls keine besitzt.
  Ableitungen
  1. Ableitung
  Die Ableitung von $e^x$ ist wiederum $e^x$ . Der Faktor $e$ bleibt bestehen.
  2. Ableitung
  Selber Vorgang wie bei der ersten Ableitung.
  Extrema bestimmen
  Da $f'(x)=e\cdot e^x$ nie Null wird, hat die Funktion keine Extrema.
  Wendepunkte bestimmen
  Da $f''(x)=e\cdot e^x$ nie Null wird, hat die Funktion keine Wendepunkte.
  Grenzwertbetrachtung
  $D_f=ℝ$
  Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm\infty$ betrachtet werden.
  gegen $+\infty$
  gegen $-\infty$
  Damit besitzt $f$ eine horizontale Asymptote bei 0 für die Annäherung an $-\infty$ .
  Symmetrieverhalten
  Ersetze $x$ durch $-x$ .
  Da $f\left(-x\right)$ weder $-f\left(x\right)$ noch $f\left(x\right)$ ist, weist die Funktion keine Symmetrie auf.
  Monotonieverhalten
  Um die Monotonie zu ermitteln, betrachte das Vorzeichen von $f'(x)$ . Da $f'(x)$ keine Nullstellen aufweist, ändert sich die Steigung von $f(x)$ auch nicht.
  Der erste Faktor $e$ ist eine Konstante und ist positiv, der zweite Faktor $e^x$ ist in $D_f=ℝ$ immer positiv, wodurch $f'(x)$ stets positiv ist.
  Damit ist die Funktion streng monoton steigend in $D_f=ℝ$ .
  Graph
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Diskutiere folgende Funktionen

$f(x)=\frac1{e^x-1}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion

Definitionsbereich festlegen

Bestimme zu erst den Definitionsbereich, indem du den Nenner der Funktion gleich $0$ setzt.

$f(x)=$ $\frac{1}{e^x-1}$

$\displaystyle e^x-1$	$=$	$\displaystyle 0$	$\displaystyle +1$
$\displaystyle e^x$	$=$	$\displaystyle 1$
	↓	Logarithmus anwenden.
$\displaystyle \ln\ \text{e}^x$	$=$	$\displaystyle \ln(1)$
$\displaystyle x\cdot\ln\text{e}\$	$=$	$\displaystyle 0$
$\displaystyle x$	$=$	$\displaystyle 0$

Somit ist der maximale Definitionsbereich $D_f = \mathbb{R}\setminus\{0\}$ .

Nullstellenbestimmung

Bestimme alle Nullstellen. Da im Zähler keine Elemente, die $x$ enthalten, vorkommen, hat die Funktion keine Nullstellen.

Ableitungen

Berechne die erste und zweite Ableitung der Funktion.

1. Ableitung

Forme zuerst $f$ ein wenig um.

$\displaystyle f\left(x\right)$	$=$	$\displaystyle \frac{1}{e^x-1}$
	↓	Eliminiere mithilfe der Potenzgesetze den Bruch.
	$=$	$\displaystyle (e^x-1)^{-1}$

Bestimme die Ableitung mithilfe der Kettenregel.

$\displaystyle f'(x)$	$=$	$\displaystyle -1\cdot\left(e^x-1\right)^{-2}\cdot e^x$
	↓	Wandle in einen Bruch um mithilfe der Potenzgesetze.
	$=$	$\displaystyle -\frac{e^x}{\left(e^x-1\right)^2}$

2. Ableitung

$f'\left(x\right)=-\frac{e^x}{\left(e^x-1\right)^2}$

Berechne die Ableitungen von Zähler ( $u'$ ) und Nenner ( $v'$ ).

$u'=e^x,\;v'=2\cdot\left(e^x-1\right)\cdot e^x$

Wende die Quotientenregel an.

$\displaystyle f''(x)$	$=$	$\displaystyle \frac{e^x\cdot\left(e^x-1\right)^2-e^x\cdot2\cdot\left(e^x-1\right)\cdot e^x}{\left(e^x-1\right)^4}$
	↓	Kürze mit $\left(e^x-1\right)$ .
	$=$	$\displaystyle \frac{e^x\cdot\left(e^x-1\right)-e^x\cdot2\cdot e^x}{\left(e^x-1\right)^3}$
	↓	Multipliziere aus.
	$=$	$\displaystyle \frac{e^{2x}-e^x-2e^{2x}}{\left(e^x-1\right)^3}$
	↓	Fasse gleiche Elemente zusammen.
	$=$	$\displaystyle \frac{-e^{2x}-e^x}{\left(e^x-1\right)^3}$
	↓	Klammere $-e^x$ aus.
	$=$	$\displaystyle -\frac{e^x\left(e^x+1\right)}{\left(e^x-1\right)^3}$

Extrema bestimmen

Zum Bestimmen der Extrema wird der Zähler der ersten Ableitung gleich Null gesetzt.

$f'\left(x\right)=-\frac{e^x}{\left(e^x-1\right)^2}$

$e^x=0$

Die $e$ -Funktion besitzt keine Nullstelle, weshalb die betrachtete Funktion keine Nullstelle besitzt.

Wendepunkte bestimmen

Zum Bestimmen der Wendepunkte wird der Zähler der zweiten Ableitung gleich Null gesetzt.

$f''(x)=-\frac{e^x\left(e^x+1\right)}{\left(e^x-1\right)^3}$

$e^x\left(e^x+1\right)=0$

Die $e$ -Funktion ist nie negativ oder gleich Null, deswegen sind weder das Innere der Klammer noch $e^x$ vor der Klammer gleich Null.

Also besitzt $f$ keine Wendepunkte.

Grenzwertbetrachtung

$D_f=\mathbb{R}\backslash\left\{0\right\}$

Da die Funktion eine Definitionslücke hat, muss das Verhalten gegen 0 und $\pm\infty$ betrachtet werden.

Grenzwert gegen $0$ von links:

$\lim_{x\rightarrow0^-}\frac1{\underbrace{\underbrace{e^x}_{\rightarrow1^-}-1}_{\rightarrow0^-}}=-\infty$

Grenzwert gegen $0$ von rechts:

$\lim_{x\rightarrow0^+}\frac1{\underbrace{\underbrace{e^x}_{\rightarrow1^+}-1}_{\rightarrow0^+}}=+\infty$

Grenzwert gegen $-\infty$ :

$\lim_{x\rightarrow-\infty}\frac1{\underbrace{e^x}_{\rightarrow0}-1}=-1$

Grenzwert gegen $+\infty$ :

$\lim_{x\rightarrow+\infty}\frac1{\underbrace{e^x}_{\rightarrow+\infty}-1}=0$

Symmetrieverhalten

Überprüfe das Symmetrieverhalten.

$f(x)=\frac1{e^x-1}$

Setze $-x$ für $x$ ein.

$\displaystyle f(-x)$	$=$	$\displaystyle \frac1{e^{-x}-1}$
	↓	Wende die Potenzgesetze an.
	$=$	$\displaystyle \frac1{{\frac1{e^x}}-1}$

Da $f(-x)$ weder $f(x)$ noch $-f(x)$ ist, ist die Funktion weder achsensymmetrisch zur $y$ -Achse noch punktsymmetrisch zum Ursprung.

Monotonieverhalten

Die Monotonie wird mithilfe einer Tabelle bestimmt:

	$x < 0$	$x = 0$	$0 < x$
Vorzeichen von $f'(x)$	-	\	-
$G_f$	$\downarrow$	\	$\downarrow$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$f(x)=e^{-x}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Definitionsbereich festlegen
Bestimme den Definitionsbereich. Da die Funktion keine Brüche, Wurzeln oder andere Dinge enthält, die den Definitionsbereich einschränken könnten, ist der Definitionsbereich der Funktion $D_f=\mathbb{R}$ .
Nullstellenbestimmung
Bestimme die Nullstellen der Funktion. Die $e$ -Funktion besitzt auf $D_f=\mathbb{R}$ keine Nullstelle, weshalb die betrachtete Funktion $f$ ebenfalls keine besitzt.
Ableitungen
Berechne die erste und zweite Ableitung der Funktion.
1. Ableitung
$f(x)=e^{-x}$
Die Ableitung von $e^{-x}$ ist $e^{-x} \cdot (-1)$ .
$f'(x)=-e^{-x}$
2. Ableitung
$f'(x)=-e^{-x}$
Die Ableitung von $-e^{-x}$ ist $-e^{-x} \cdot (-1)$ .
$f''(x)=e^{-x}$
Extrema bestimmen
Bestimme die Extrema.
Da $f'(x)=-e^{-x}$ nie Null wird, hat die Funktion keine Extrema.
Wendepunkte bestimmen
Bestimme die Wendepunkte.
Da $f''(x)=e^{-x}$ nie Null wird, hat die Funktion keine Wendepunkte.
Grenzwertbetrachtung
$D_f=\mathbb{ℝ}$
Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm\infty$ betrachtet werden.
Grenzwert gegen $+\infty$ :
$\lim_{x\to\infty} \underbrace{e^{-x}}_{\to 0} = 0$
Damit besitzt $f$ eine horizontale Asymptote bei 0 für die Annäherung an $-\infty$ .
Grenzwert gegen $-\infty$ :
$\lim_{x\to-\infty}\underbrace{e^{-x}}_{\to \infty}=\infty$
Symmetrieverhalten
Untersuche das Symmetrieverhalten.
$f(x)=e^{-x}$
Ersetze $x$ durch $-x$ .
$f(-x)=e^{-(-x)}=e^x$
Da $f\left(-x\right)$ weder $-f\left(x\right)$ noch $f\left(x\right)$ ist, weist die Funktion keine Symmetrie auf.
Monotonieverhalten
Um die Monotonie zu ermitteln, betrachte das Vorzeichen von $f'(x)$ .
Da $f'(x)$ keine Nullstellen aufweist, ändert sich die Steigung von $f(x)$ auch nicht. Betrache die Steigung daher an einer beliebigen Stelle, z. B. $x=0$ :
Damit ist die Funktion streng monoton fallend in $D_f = \mathbb{R}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme Definitionsbereich, Nullstellen und Extrema der folgenden Funktion:

$\displaystyle f\left(x\right)=\frac{e^x-4}{e^{2x}-5}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: E-Funktion

Definitionsbereich festlegen

Zunächst legst du den Defintionsbereich fest:

$\displaystyle f\left(x\right)=\dfrac{e^x-4}{e^{2x}-5}$

Setze den Nenner der Funktion gleich 0.

$\displaystyle e^{2x}-5$	$=$	$\displaystyle 0$	$\displaystyle +5$
$\displaystyle e^{2x}$	$=$	$\displaystyle 5$
	↓	Wende den Logarithmus an.
$\displaystyle 2x$	$=$	$\displaystyle \ln(5)$	$\displaystyle :2$
$\displaystyle x$	$=$	$\displaystyle \displaystyle \frac{\ln(5)}{2}$

Damit ist der maximale Definitionsbereich $D_f=\mathbb{R}\setminus\left\{\frac{\ln(5)}2\right\}$ .

Nullstellenbestimmung

Bestimme nun die Nullstellen von f:

$\displaystyle f\left(x\right)=\frac{e^x-4}{e^{2x}-5}$

Setze den Zähler der Funktion gleich 0.

$\displaystyle e^x-4$	$=$	$\displaystyle 0$	$\displaystyle +4$
$\displaystyle e^x$	$=$	$\displaystyle 4$
	↓	Wende den Logarithmus an.
$\displaystyle x$	$=$	$\displaystyle \ln(4)$

Die einzige Nullstelle ist $(\ln(4)\mid0)$ .

Ableitungen

Bilde die erste und zweite Ableitung von f:

1. Ableitung

$\displaystyle f\left(x\right)=\frac{e^x-4}{e^{2x}-5}$

$u'=e^x,\;v'=2e^{2x}$

Wende die Quotientenregel an.

$\displaystyle f'\left(x\right)$	$=$	$\displaystyle \displaystyle \frac{e^x\cdot\left(e^{2x}-5\right)-2e^{2x}\cdot\left(e^x-4\right)}{\left(e^{2x}-5\right)^2}$
	↓	Löse die Klammern auf.
	$=$	$\displaystyle \displaystyle \frac{e^{3x}-5e^x-2e^{3x}+8e^{2x}}{\left(e^{2x}-5\right)^2}$
	↓	Fasse gleiche Elemente zusammen.
	$=$	$\displaystyle \displaystyle \frac{-e^{3x}+8e^{2x}-5e^x}{\left(e^{2x}-5\right)^2}$

2. Ableitung

$\displaystyle f'\left(x\right)=\frac{-e^{3x}+8e^{2x}-5e^x}{\left(e^{2x}-5\right)^2}$

Berechne die Ableitung von Zähler ( $u'$ ) und Nenner ( $v'$ ).

$u'=-3e^{3x}+16e^{2x}-5e^x,\;v'=\left(e^{2x}-5\right)\cdot2\cdot2e^{2x}$

Wende die Quotientenregel an.

$\displaystyle f''(x)$	$=$	$\displaystyle \displaystyle \frac{(-3e^{3x}+16e^{2x}-5e^x)\cdot(e^{2x}-5)^2-(e^{2x}-5)\cdot2\cdot2e^{2x}\cdot(-e^{3x}+8e^{2x}-5e^x)}{(e^{2x}-5)^4}$
	↓	Kürze mit $\left(e^{2x}-5\right)$ .
	$=$	$\displaystyle \displaystyle \frac{\left(-3 e^{3 x}+16 e^{2 x}-5 e^ x\right)\cdot\left( e^{2 x}-5\right)-2\cdot2 e^{2 x}\cdot\left(- e^{3 x}+8 e^{2 x}-5 e^ x\right)}{\left( e^{2 x}-5\right)^3}$
	↓	Löse die Klammern auf.
	$=$	$\displaystyle \displaystyle \frac{-3e^{5x}+16e^{4x}-5e^{3x}+15e^{3x}-80e^{2x}+25e^x+4e^{5x}-32e^{4x}+20e^{3x}}{\left(e^{2x}-5\right)^3}$
	↓	Fasse gleiche Elemente zusammen.
	$=$	$\displaystyle \displaystyle \frac{e^{5x}-16e^{4x}+30e^{3x}-80e^{2x}+25e^x}{\left(e^{2x}-5\right)^3}$

Extrema bestimmen

Nun werden die Extrema bestimmt:

$\displaystyle f'\left(x\right)=\frac{-e^{3x}+8e^{2x}-5e^x}{\left(e^{2x}-5\right)^2}$

Es wird nur der Zähler der 1. Ableitung gleich 0 gesetzt, da ein Bruch 0 wird, wenn der Zähler 0 wird.

$-e^{3x}+8e^{2x}-5e^x=0$

Substitution

Verwende die Substitution.

$u=e^x$

$-u^3+8u^2-5u=0$

Klammere $u$ aus.

$u\cdot\left(-u^2+8u-5\right)=0$

Ein Produkt wird 0, wenn einer der Faktoren 0 wird.

$\;\;\Rightarrow\;\;u_1=0$

Für weitere Extrema wird nur das Innere der Klammer betrachtet.

$-u^2+8u-5=0$

Wende die Mitternachtsformel an.

$\displaystyle u_{2{,}3}$	$=$	$\displaystyle \displaystyle \frac{-8\pm\sqrt{64-4\cdot\left(-1\right)\cdot\left(-5\right)}}{2\cdot\left(-1\right)}$
	↓	Unter der Wurzel subtrahieren .
	$=$	$\displaystyle \frac{-8\pm\sqrt{44}}{-2}$
	↓	2 lässt sich aus der Wurzel ziehen.
	$=$	$\displaystyle \frac{-8\pm2\sqrt{11}}{-2}$

$\phantom{u_{2{,}3}}$

$\displaystyle u_2=\frac{-8+2\sqrt{11}}{-2}=4-\sqrt{11}$

$\displaystyle u_3=\frac{-8-2\sqrt{11}}{-2}=4+\sqrt{11}$

Resubstitution

Verwende nun die Resubstitution:

$u_1=e^{x_1}$

$0=e^{x_1}$

Die Exponentialfunktion ist immer größer als 0. Die Gleichung ist daher nicht lösbar und $x_1$ keine Nullstelle.

$u_2=e^{x_2}$

$4-\sqrt{11}=e^{x_2}$

Wende den Logarithmus an.

$\ln\left(4-\sqrt{11}\right)=x_2$

$u_3=e^{x_3}$

$4+\sqrt{11}=e^{x_3}$

Wende den Logarithmus an.

$\ln(4+\sqrt{11})=x_3$

$y$ -Werte bestimmen

$\displaystyle f\left(x\right)=\frac{e^x-4}{e^{2x}-5}$

$x_2$ einsetzen.

$\displaystyle f\left(\ln\left(4-\sqrt{11}\right)\right)$	$=$	$\displaystyle \displaystyle \frac{\mathrm{e}^{\ln\left(4-\sqrt{11}\right)}-4}{\mathrm{e}^{2\cdot\ln\left(4-\sqrt{11}\right)}-5}=\frac{4-\sqrt{11}-4}{\left(4-\sqrt{11}\right)^2-5}$
	$=$	$\displaystyle \displaystyle \frac{-\sqrt{11}}{16-8\sqrt{11}+11-5}=\frac{-\sqrt{11}}{22-8\sqrt{11}}$
	$=$	$\displaystyle \displaystyle \frac{1}{8-2\sqrt{11}}$

Erster Extrempunkt

$\left(\ln\left(4-\sqrt{11}\right)\ \left|\ \frac1{8-2\sqrt{11}}\right)\right.$

$\displaystyle f\left(x\right)=\frac{e^x-4}{e^{2x}-5}$

$x_3$ einsetzen.

$\displaystyle f\left(\ln\left(4+\sqrt{11}\right)\right)$	$=$	$\displaystyle \displaystyle \frac{e^{\ln\left(4+\sqrt{11}\right)}-4}{e^{2\cdot\ln\left(4+\sqrt{11}\right)}-5}$
	$=$	$\displaystyle \displaystyle \frac{4+\sqrt{11}-4}{\left(4+\sqrt{11}\right)^2-5}=\frac{\sqrt{11}}{22+8\sqrt{11}}$
	$=$	$\displaystyle \displaystyle \frac{1}{8+2\sqrt{11}}$

Zweiter Extrempunkt

$\left(\ln\left(4+\sqrt{11}\right)\ \left|\ \frac1{8+2\sqrt{11}}\right.\right)$

Art der Extrema bestimmen

$f''\left(x\right)= \displaystyle \frac{e^{5x}-16e^{4x}+30e^{3x}-80e^{2x}+25e^x}{\left(e^{2x}-5\right)^3}$

Setze $x_2$ ein.

$\Rightarrow \left(\ln\left(4-\sqrt{11}\right)\ \left|\ \displaystyle \frac1{8-2\sqrt{11}}\right)\right.$

Die 2. Ableitung ist größer 0, da Zähler und Nenner beide kleiner 0 sind. Also liegt an der Stelle $x_2$ ein Tiefpunkt vor.

$f''\left(\ln(4+\sqrt{11})\right) = \displaystyle \frac{e^{5 \cdot \ln(4+\sqrt{11})}-16e^{4 \cdot \ln(4 +\sqrt{11})}+30e^{3 \cdot \ln(4 +\sqrt{11})}-80e^{2 \cdot \ln(4 + \sqrt{11})}+25e^{\ln(4+\sqrt{11})}}{(e^{2 \cdot \ln(4-\sqrt{11})} + 5)^3}$

$\Rightarrow \left(\ln\left(4+\sqrt{11}\right)\ \left|\ \frac1{8+2\sqrt{11}}\right.\right)$

Die 2. Ableitung ist kleiner 0, da der Zähler kleiner und der Nenner größer 0 ist. Also liegt an der Stelle $x_3$ ein Hochpunkt vor.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zur Diskussion von e-Funktionen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung des Schnittwinkels zweier reeller Funktionen in einem Punkt:

(*) Alternativer Lösungsweg

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1. Ableitung

2. Ableitung

Grenzwertbetrachtung

gegen +∞+\infty+∞

gegen −∞-\infty−∞

Hast du eine Frage oder Feedback?

Definitionsbereich festlegen

Nullstellenbestimmung

Ableitungen

1. Ableitung

2. Ableitung

Extrema bestimmen

Wendepunkte bestimmen

Grenzwertbetrachtung

Symmetrieverhalten

Monotonieverhalten

Hast du eine Frage oder Feedback?

Definitionsbereich festlegen

Nullstellenbestimmung

Ableitungen

1. Ableitung

2. Ableitung

Extrema bestimmen

Wendepunkte bestimmen

Grenzwertbetrachtung

Monotonieverhalten

Hast du eine Frage oder Feedback?

Definitionsbereich festlegen

Nullstellenbestimmung

Ableitungen

1. Ableitung

2. Ableitung

Extrema bestimmen

Substitution

Resubstitution

yyy-Werte bestimmen

Art der Extrema bestimmen

gegen $+\infty$

gegen $-\infty$

$y$ -Werte bestimmen