Aufgaben zur Nullstelle

Lies die Nullstelle(n) folgender Funktionen ab

$f (x) = 2 x - 8$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Hier wird die Nullstelle erst graphisch und dann rechnerisch bestimmt.
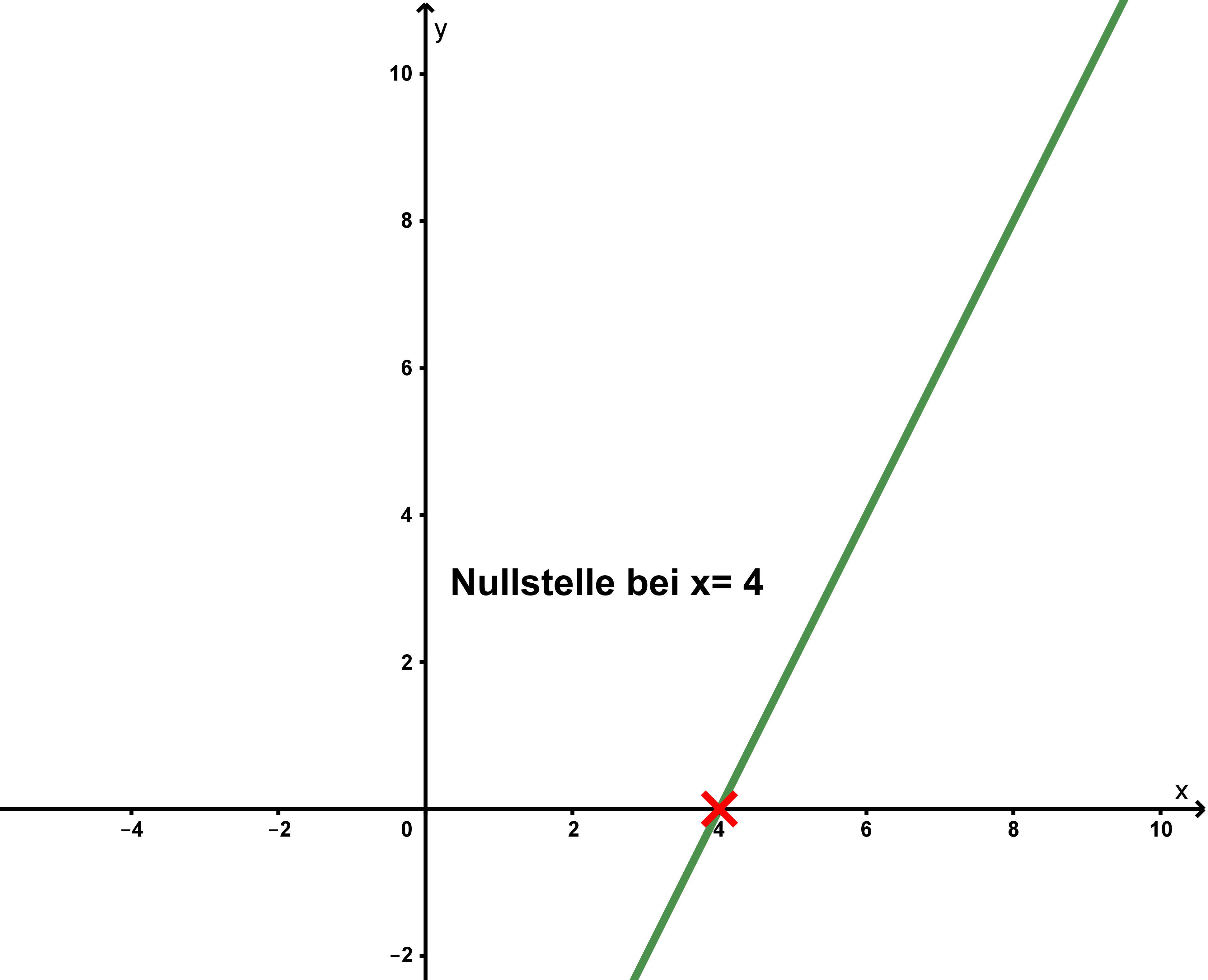
Man sieht, dass der Graph der Funktion $f$ die x-Achse genau im Punkt (4|0) schneidet.
$\Rightarrow$ Nullstelle bei $x = 4$ .
Graphische Veranschaulichung:
Lösung durch Berechnung:
$f (x)$ $=$ $2 x - 8$
↓
Setze $f (x) = 0$
$2 x - 8$ $=$ $0$ $+ 8$
$2 x$ $=$ $8$ $: 2$
$x$ $=$ $4$
Die Nullstelle der Funktion liegt bei $x = 4$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$g (x) = - x^{2} - 7 x - 10$

$h (x) = \frac{1}{10} (x + 6) (x - 2) (x - 4)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.
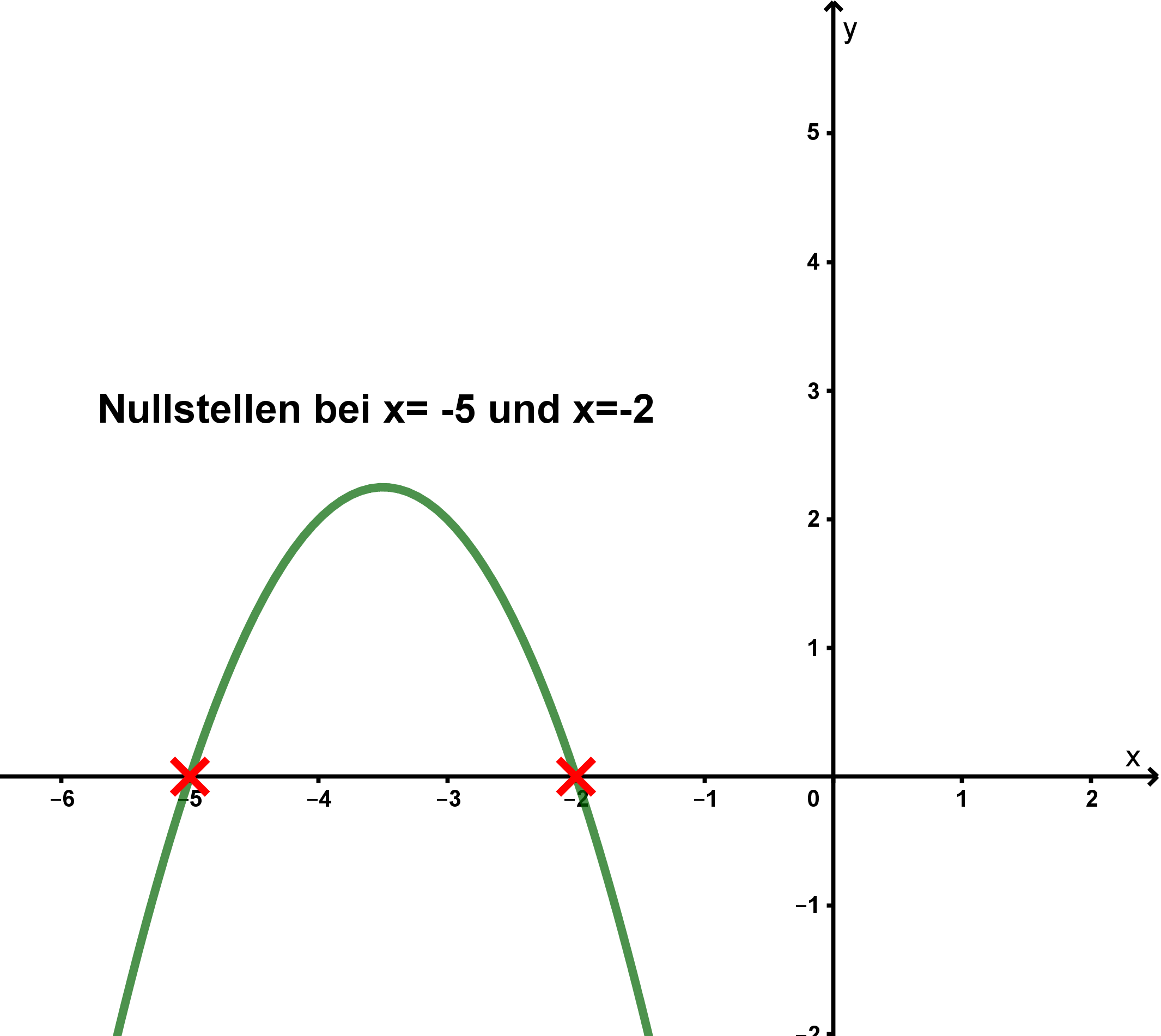
Man sieht, dass der Graph der Funktion $f$ die x-Achse genau in den Punkten (-6|0), (2|0) und (4|0) schneidet.
⇒ Nullstellen bei $x = - 6$ und $x = 2$ und $x = 4$ .
Graphische Veranschaulichunng
Lösung durch Berechnung:
$h (x) = \frac{1}{10} (x + 6) (x - 2) (x - 4)$
Zur Berechnung der Nullstellen setze $h (x) = 0$ .
$\frac{1}{10} (x + 6) (x - 2) (x - 4) = 0$
Ein Produkt aus mehreren Faktoren ist immer dann $0$ , wenn mindestens ein Faktor $0$ ist.
Für $x = - 6$ , $x = 2$ und $x = 4$ gilt:
$\frac{1}{10} (x + 6) (x - 2) (x - 4) = 0$
Die Nullstellen der Funktion liegen bei $x = - 6$ , $x = 2$ und $x = 4$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f (x) = 3 x^{2} + 6 x + 3$

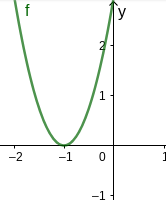
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.
Man sieht, dass der Graph der Funktion f die x-Achse genau in einem Punkt (-1|0) berührt.
⇒ Nullstelle bei x=−1.
Graphische Veranschaulichung
Lösung durch Berechnung
$f (x) = 3 x^{2} + 6 x + 3$
Zur Berechnung der Nullstellen setze $f (x) = 0$ .
$3 x^{2} + 6 x + 3 = 0$
Kürze durch 3.
$x^{2} + 2 x + 1 = 0$
Ermittle die Lösung durch die Mitternachtsformel:
$x_{1,2} = \frac{- 2 \pm \sqrt{(2)^{2} - 4 \cdot 1 \cdot 1}}{2 \cdot 1}$
$x_{1,2} = \frac{- 2 \pm \sqrt{0}}{2 \cdot 1} = \frac{- 2 \pm 0}{2} = - 1$
$\Rightarrow x_{1} = - 1$
Die Nullstelle liegt also bei $x_{1} = - 1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

2
Bestimme die Vielfachheiten der Nullstelle(n) zu folgenden Funktionen
1. $f (x) = x^{7}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
  $f (x) = x^{7}$
  Zerlege $f (x)$ in Linearfaktoren
  $f (x) = (x \pm 0)^{7}$
  Lies die Vielfachheit der Nullstelle am Exponenten ab.
  Die Funktion $f (x) = x^{7}$ hat bei $x = 0$ eine Nullstelle der Vielfachheit 7.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
2. $f (x) = 6 x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
  $f (x) = 6 x$
  Zerlege $f (x)$ in Linearfaktoren
  $f (x) = 6 \cdot (x \pm 0)^{1}$
  Lies die Vielfachheit der Nullstelle am Exponenten ab.
  Die Funktion $f (x) = 6 x$ hat bei $x = 0$ eine einfache Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
3. $f (x) = (x - 5)^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
  $f (x) = (x - 5)^{2}$
  $f (x)$ ist bereits in der Linearfaktordarstellung. Deshalb kannst du die Vielfachheit der Nullstelle direkt am Exponenten ablesen.
  Die Funktion $f (x) = (x - 5)^{2}$ hat bei $x = 5$ eine doppelte Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
4. $f (x) = x^{2} - 9$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
  $f (x) = x^{2} - 9$
  Zerlege $f (x)$ in Linearfaktoren.
  Verwende die 3. binomischen Formel.
  $f (x) = (x - 3) \cdot (x + 3)$
  $f (x) = (x - 3)^{1} \cdot (x + 3)^{1}$
  Lies aus der Linearfaktordarstellung die Vielfachheiten der Nullstellen an den Exponenten ab.
  Die Funktion $f (x) = x^{2} - 9$ hat bei $x = - 3$ und $x = 3$ jeweils eine einfache Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
5. $f (x) = (x + 8) \cdot (x - 2)^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit einer Nullstelle
  $f (x) = (x + 8) \cdot (x - 2)^{2}$
  $f (x)$ ist schon in Linearfaktordarstellung. Du kannst also die Vielfachheiten der Nullstellen direkt an den Exponenten ablesen.
  Die Funktion $f (x) = (x + 8)^{1} \cdot (x - 2)^{2}$ hat bei $x = - 8$ eine einfache und bei $x = 2$ eine doppelte Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Vielfachheit der Nullstellen mit Hilfe der Linearfaktorzerlegung.
3
Bestimme die Intervalle auf der $x$ -Achse, in denen der Graph der folgenden Funktionen oberhalb der $x$ -Achse verläuft.
1. $f (x) = x \cdot (x^{2} - 9)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Gegeben: $f (x) = x \cdot (x^{2} - 9)$
  Gesucht: Intervalle für die $f (x) > 0$
  Faktorisiere zuerst $f$ . Dies geht hier mit der 3. binomischen Formel $(a^{2} - b^{2}) = (a + b) \cdot (a - b)$
  $f (x) = x \cdot (x^{2} - 9) = x \cdot (x + 3) \cdot (x - 3)$
  Bestimme die Vielfachheiten der Nullstellen
  Die drei Nullstellen bei $x_{1} = 0, x_{2} = - 3, x_{3} = 3$ sind einfache Nullstellen.
  Bestimme jetzt noch das Vorzeichen in einem Bereich. Zum Beispiel in dem Bereich $] 3, + \infty [$
  Für $x$ im Intervall $] 3, + \infty [$ ist $f (x)$ positiv, denn:
  $f (x) = \underset{> 0}{\underset{⏟}{x}} \cdot \underset{> 0}{\underset{⏟}{(x + 3)}} \cdot \underset{> 0}{\underset{⏟}{(x - 3)}}$
  Einfache Nullstelle bei $x = 3$ , also ist der Graph im Intervall $] 0,3 [$ im negativen Bereich.
  Einfache Nullstelle bei $x = 0$ , also ist der Graph im Intervall $] - 3,0 [$ im positiven Bereich.
  Einfache Nullstelle bei $x = 3$ , also ist der Graph im Intervall $] - \infty, - 3 [$ im negativen Bereich.
  Lösung: Der Graph verläuft in den Intervallen $] - 3,0 [$ und $] 3, + \infty [$ oberhalb der $x$ -Achse
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $g (x) = 0,5 \cdot (x^{2} - 8 x + 16) \cdot (x + 1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Gegeben: $f (x) = 0,5 \cdot (x^{2} - 8 x + 16) \cdot (x + 1)$
  Gesucht: Intervalle mit $f (x) > 0$
  Faktorisiere zuerst den Term. Dies geht hier mit der 2. binomischen Formel $(a^{2} - 2 a b + b^{2}) = (a - b)^{2}$ .
  $f (x) = 0,5 \cdot (x - 4)^{2} \cdot (x + 1)$
  Bestimme die Vielfachheiten der Nullstellen.
  Die Nullstelle bei $x_{1} = 4$ ist eine doppelte Nullstelle, die bei $x_{2} = - 1$ ist eine einfache.
  Bestimme jetzt noch das Vorzeichen in einem Bereich. Zum Beispiel in dem Bereich $] 4, + \infty [$ .
  Für $x$ im Intervall $] 4, + \infty [$ ist $f (x) > 0$ , denn:
  $f (x) = \underset{> 0}{\underset{⏟}{0,5}} \cdot \underset{> 0}{\underset{⏟}{(x - 4)^{2}}} \cdot \underset{> 0}{\underset{⏟}{(x + 1)}}$
  Bestimme jetzt den Verlauf mithilfe der Vielfachheiten.
  Weil bei $4$ eine doppelte Nullstelle ist, ändert sich da das Vorzeichen nicht.
  Doppelte Nullstelle bei $x = 4$ , also ist der Graph im Intervall $] - 1,4 [$ ebenfalls im positiven Bereich.
  Weil bei $- 1$ eine einfache Nullstelle ist, ändert sich dort das Vorzeichen.
  Einfache Nullstelle bei $x = - 1$ , also ist der Graph im Intervall $] - \infty, - 1 [$ im negativen Bereich.
  Lösung: Der Graph ist in den Intervallen $] - 1,4 [$ und $] 4, + \infty [$ oberhalb der $x$ -Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $h (x) = 0.1 \cdot (x + 2.5) \cdot (x^{2} - x + \frac{1}{4}) \cdot (x - 4)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Gegeben: $f (x) = 0,1 \cdot (x + 2,5) \cdot (x^{2} - x + \frac{1}{4}) \cdot (x - 4)$
  Geuscht: Intervalle mit $f (x) > 0$
  Faktorisiere zuerst den Term. Dies geht hier mit der 2. binomischen Formel $(a^{2} - 2 a b + b^{2}) = (a - b)^{2}$
  Dabei ist $a = x$ und $b = \frac{1}{2}$
  $f (x) = 0,1 \cdot (x + 2,5) \cdot (x - \frac{1}{2})^{2} \cdot (x - 4)$
  Bestimme die Vielfachheiten der Nullstellen
  Die Nullstelle bei $x_{1} = - 2,5$ ist eine einfache, die bei $x_{2} = \frac{1}{2}$ eine doppelte und die bei $x_{3} = 4$ wieder eine einfache Nullstelle.
  Bestimme jetzt noch das Vorzeichen in einem Bereich. Zum Beispiel in dem Bereich $] 4, + \infty [$
  Für $x$ im Intervall $] 4, + \infty [$ ist $f (x)$ positiv, denn:
  $f (x) = \underset{> 0}{\underset{⏟}{0,1}} \cdot \underset{> 0}{\underset{⏟}{(x + 2,5)}} \cdot \underset{> 0}{\underset{⏟}{(x - 12)^{2}}} \cdot \underset{> 0}{\underset{⏟}{(x - 4)}}$
  Bestimme jetzt den Verlauf mithilfe der Vielfachheiten.
  Weil bei $4$ eine einfache Nullstelle ist, ändert sich dort das Vorzeichen.
  Einfache Nullstelle bei $x = 4$ , also ist der Graph im Intervall $] \frac{1}{2}, 4 [$ im negativen Bereich.
  Weil bei $\frac{1}{2}$ eine doppelte Nullstelle ist, ändert sich dort das Vorzeichen nicht.
  Doppelte Nullstelle bei $x = \frac{1}{2}$ , also ist der Graph im Intervall $] - 2,5, \frac{1}{2} [$ ebenfalls im negativen Bereich.
  Weil bei $- 2,5$ eine einfache Nullstelle ist, ändert sich dort das Vorzeichen.
  Einfache Nullstelle bei $x = - 2,5$ , also ist der Graph im Intervall $] - \infty, - 2,5 [$ im positiven Bereich.
  Lösung: Der Graph ist in den Intervallen $] - \infty, - 2,5 [$ und $] 4, + \infty [$ im positiven Bereich.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Skizziere mit Hilfe den gegebenen Informationen jeweils einen möglichen Verlaufdes Graphen der folgenden Funktionen.
1. Die Polynomfunktion $f$ vom Grad $3$ besitzt Nullstellen bei $x_{1} = - 3$ , $x_{2} = 2$ und $x_{3} = 4$ und schneidet die $y$ -Achse im Punkt $(0 | 2)$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Gegeben:
  Polynomfunktion vom Grad $3$
  Nullstellen bei $x_{1} = - 3, x_{2} = 2, x_{3} = 4$ und Punkt $(0,2)$
  Gesucht: Skizze von Graph
  Zeichne zuerst die gegebenen Punkte in ein Koordinatensystem. Die Nullstellen liegen auf der $x$ -Achse.
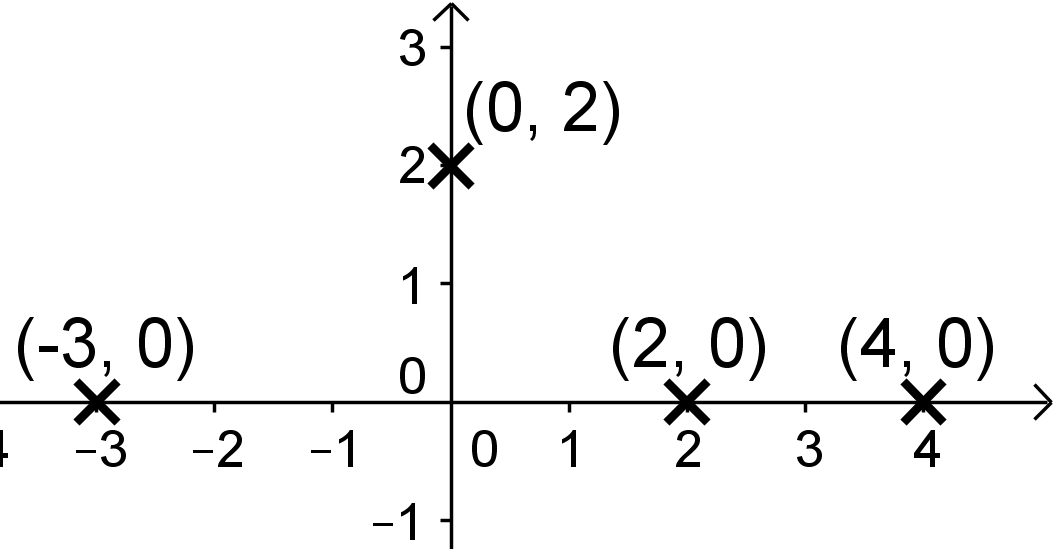
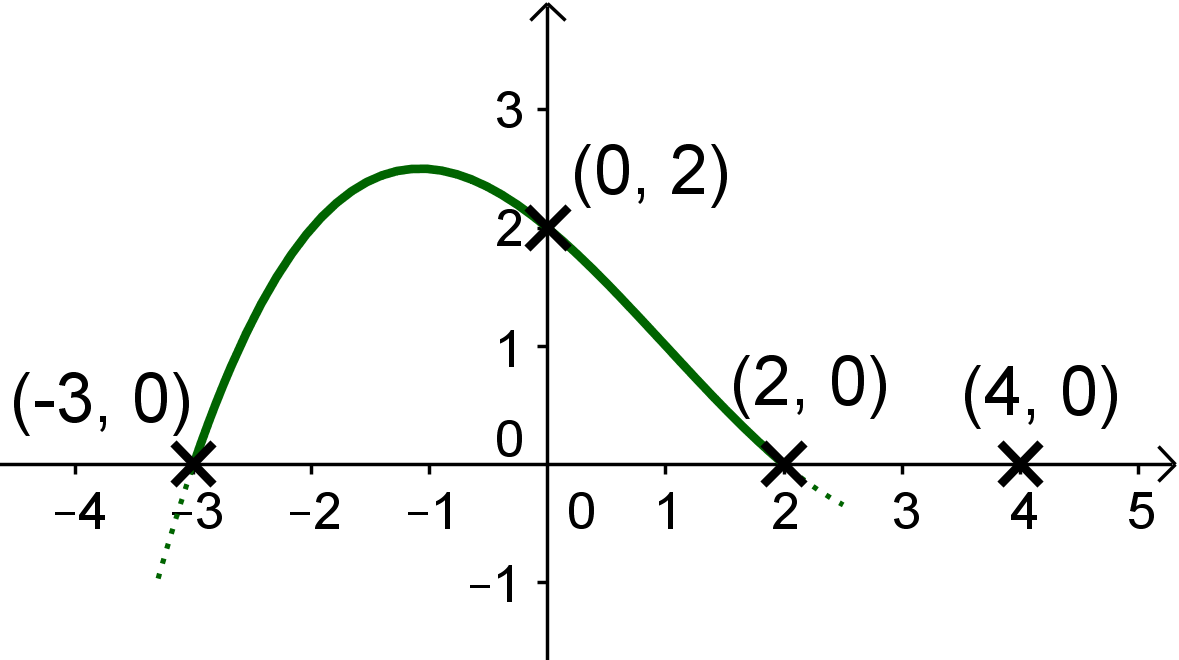
  Da die Funktion vom Grad $3$ ist, kann es keine weiteren Nullstellen geben und die drei Nullstellen sind einfache Nullstellen.
  Der Verlauf geht also von $(- 3,0)$ zu $(0,2)$ und dann zu $(2,0)$ . Wichtig ist, dass er NICHT nochmal die $x$ -Achse schneidet. Wo der Hochpunkt zwischen $- 3$ und $2$ genau ist, ist egal.
  Zeichne als Nächstes den Graph zwischen $2$ und $4$ weiter. Dort verläuft er im negativen Bereich. Auch hier ist egal, wo der Tiefpunkt zwischen $2$ und $4$ genau ist.
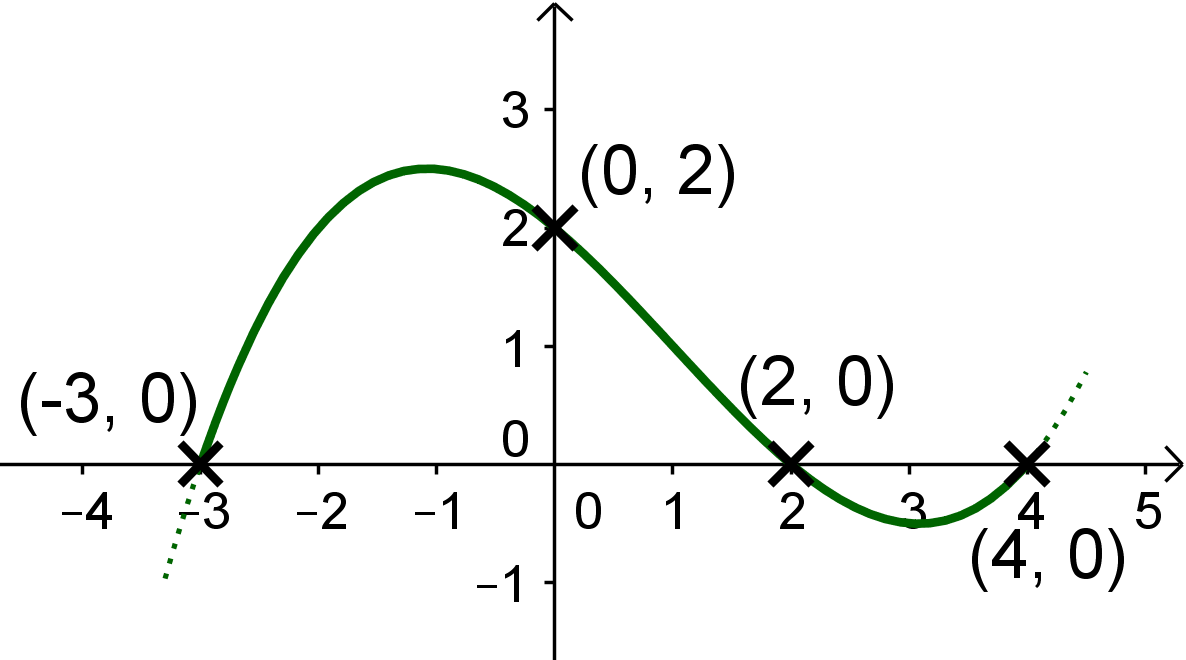
  Zeichne jetzt den ganzen Graphen. Auch $(- 3,0)$ und $(4,0)$ sind einfache Nullstellen, also schneidet der Graph die x-Achse.
  Lösung:
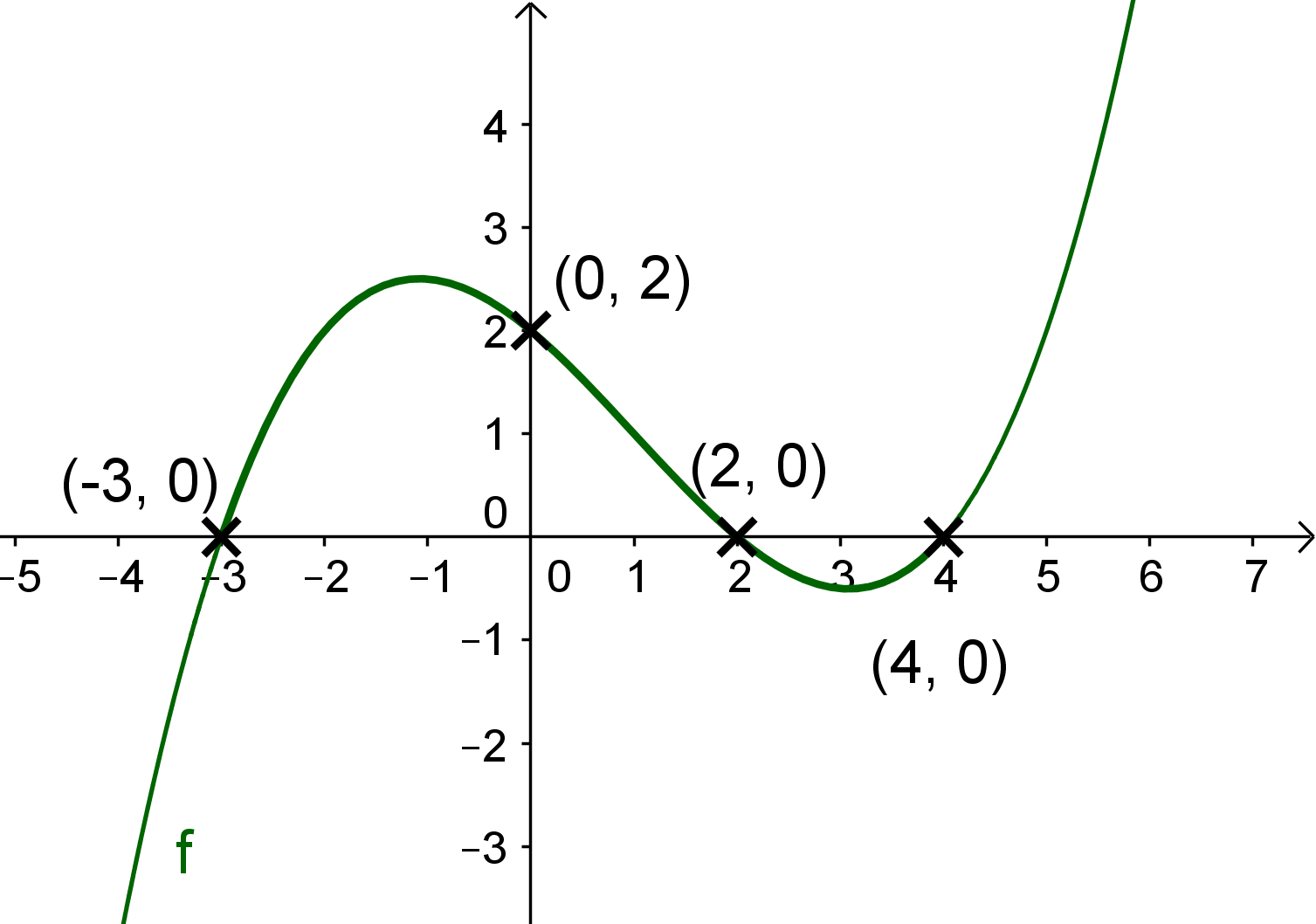
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Polynomfunktion $g$ vom Grad $4$ hat genau eine doppelte Nullstelle und ihr Graph ist symmetrisch zur $y$ -Achse.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Gegeben: Polynomfunktion vom Grad $4$ , genau eine doppelten Nullstelle, und der Graph symmetrisch zur $y$ -Achse
  Gesucht: Skizze eines möglichen Graphen
  Überlege zunächst, wo die doppelte Nullstelle hinkommt. Da der Graph symmetrisch zur $y$ -Achse ist, muss sie bei $(0,0)$ sein, denn wenn sie z.B. bei $(2,0)$ wäre, müsste durch die Symmetrie bei $(- 2,0)$ auch eine sein. Ob der Graph die $x$ -Achse von unten oder von oben berührt, ist beides richtig.
  Zeichne jetzt den weiteren Verlauf.
  Beachte dabei: Die Funktion ist vom Grad $4$ , also hat sie höchstens zwei weitere Nullstellen. Außerdem auch nur maximal $3$ Extremstellen.
  Eine mögliche Lösung:
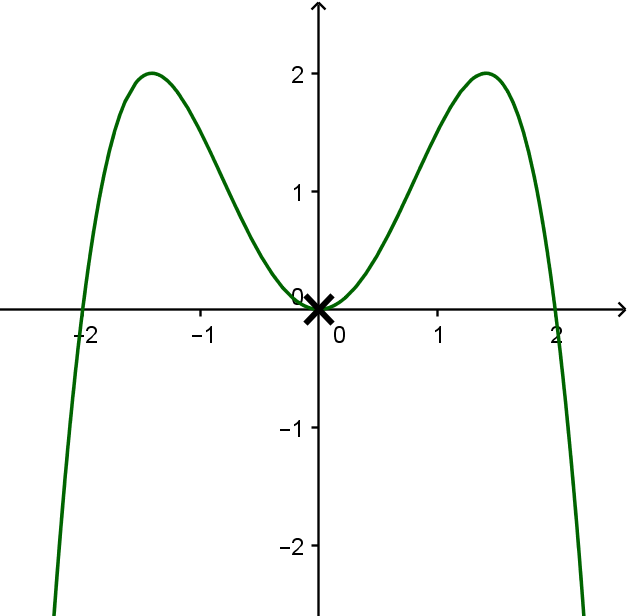
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Die Polynomfunktion $h$ vom Grad $6$ besitzt zwei mehrfache Nullstellen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Gegeben: Polynomfunktion vom Grad $6$ , zwei mehrfache Nullstellen
  Gesucht: Skizze von möglichem Graphen
  Bei dieser Aufgabe gibt es viele verschiedene Möglichkeiten, hier wird eine $3$ -fache Nullstelle bei $x = - 1$ und eine doppelte Nullstelle bei $x = 2$ verwendet.
  Du kannst aber beispielsweise auch zwei $3$ -fache Nullstellen einzeichnen, oder zwei doppelte, oder eine doppelte und eine $4$ -fache.
  Skizziere als Erstes den Verlauf der Funktion an einer Nullstelle.
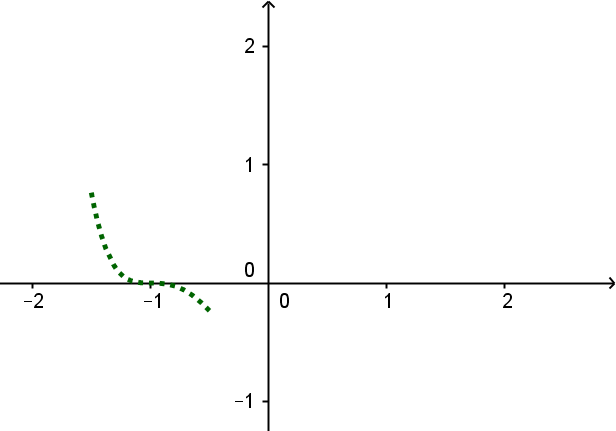
  Überlege dann den Verlauf zur zweiten Nullstelle und wie er dort weiterläuft.
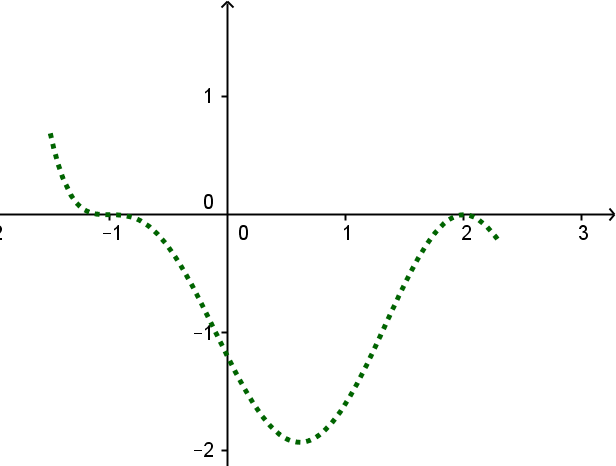
  Ergänze jetzt den Graphen noch so, dass er zu einer Funktion vom Grad $6$ passt. Dabei ist wichtig, dass der Graph entweder auf beiden Seiten nach $+ \infty$ oder auf beiden Seiten nach $- \infty$ läuft.
  Achte darauf, dass die Vielfachheiten der Nullstellen insgesamt höchstens $6$ ergeben. Hier ist es eine $3$ -fache, eine doppelte und noch eine einfache Nullstelle.
  Eine mögliche Lösung
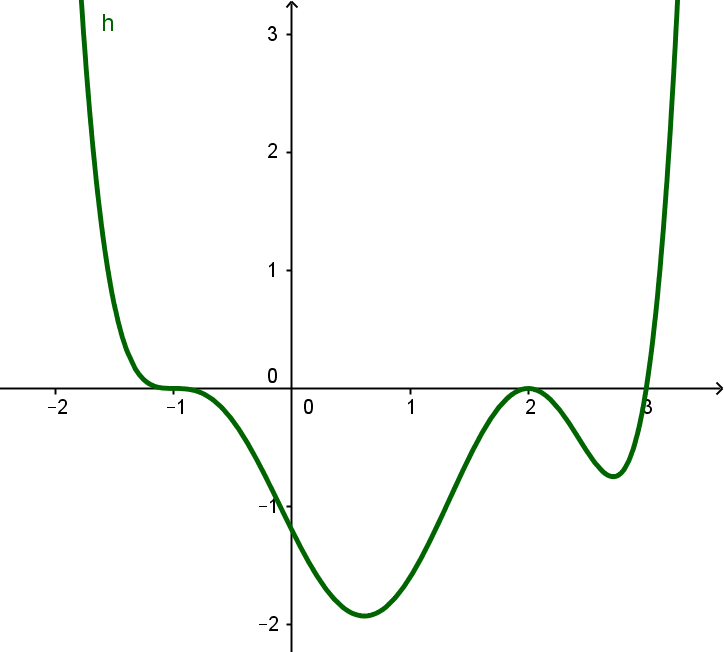
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
Ordne die Graphen jeweils dem richtigen Funktionsterm zu. Begründe deine Antwort.
$f (x) = 0,1 \cdot (x + 2)^{2} \cdot (x - 4)^{3}$
$g (x) = - 0,1 \cdot (x + 2)^{2} \cdot (x - 4)$
$h (x) = - 0,01 \cdot (x + 2)^{3} \cdot (x - 4)^{2} \cdot (x - 2)$
$j (x) = 0,05 \cdot (x + 2) \cdot (x - 4) \cdot (x^{2} + 1)$
$k (x) = - 0,01 \cdot (x + 2)^{4} \cdot (x - 4)^{2} \cdot (x - 2)$

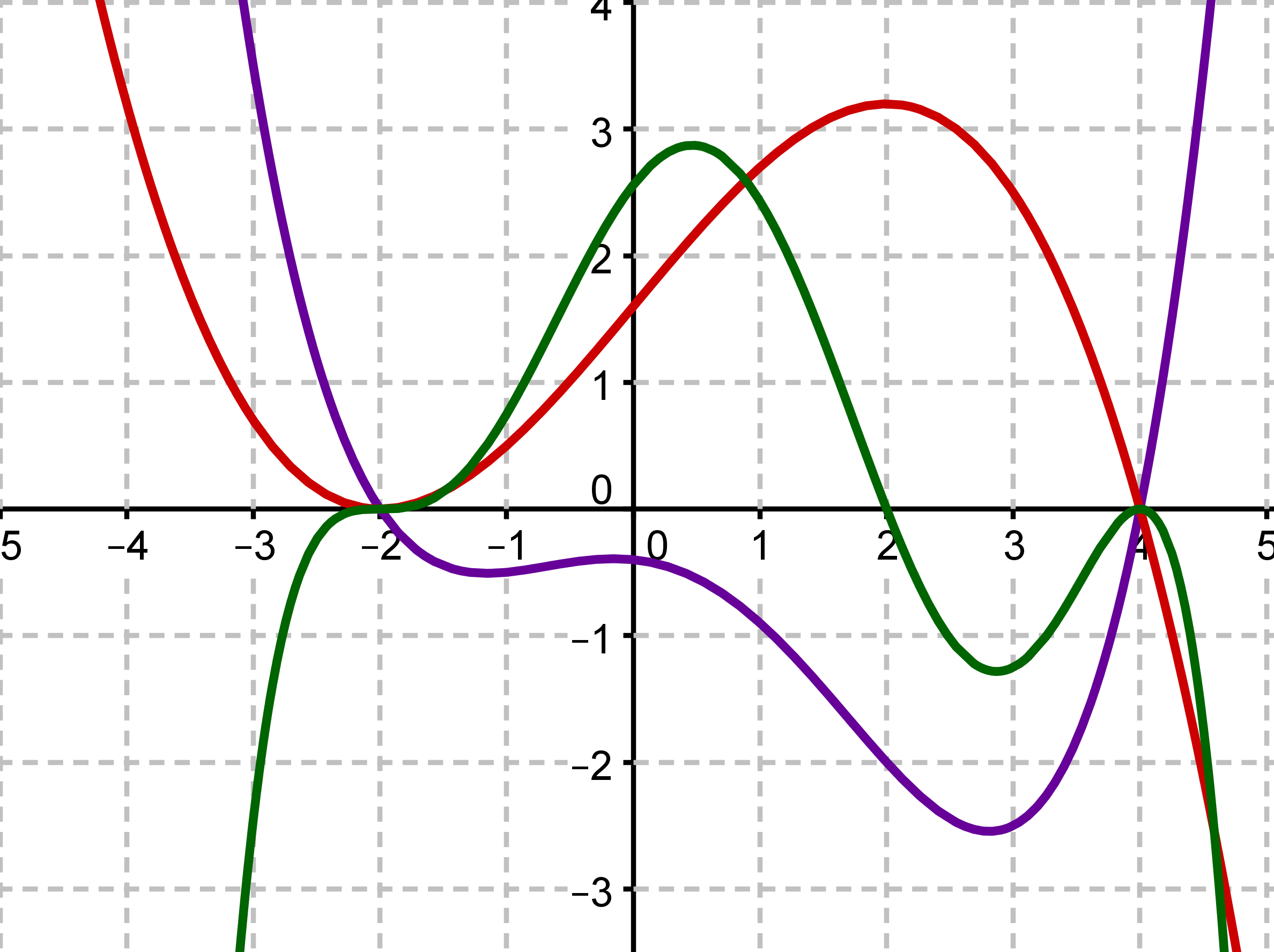
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit von Nullstellen
Roter Graph
Lies als Erstes die Nullstellen der Funktion ab.
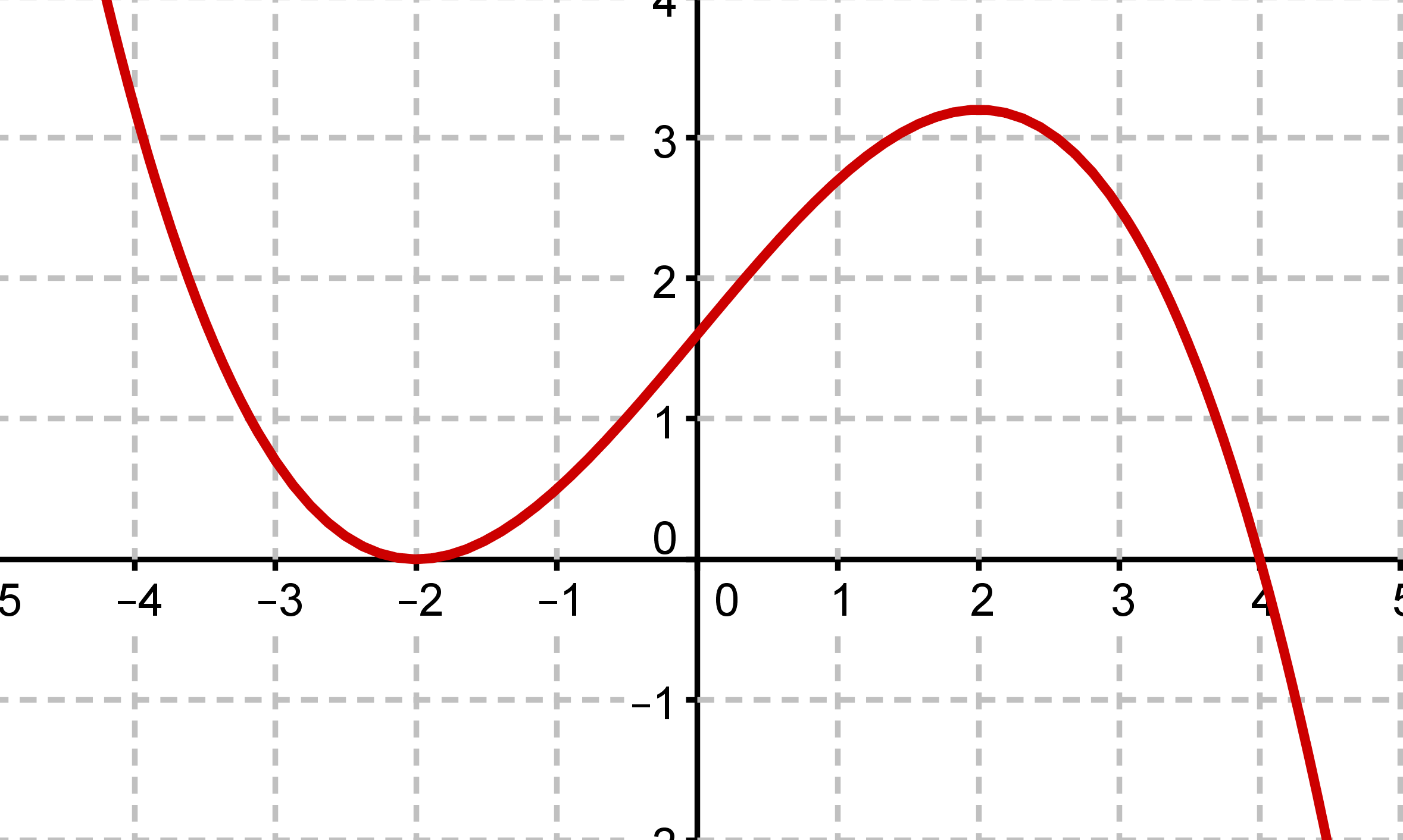
Die Nullstellen des roten Graphen sind bei $x_{1} = - 2$ und $x_{2} = 4$ .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstelle bei $x_{1} = - 2$ ist eine doppelte Nullstelle, weil sich das Vorzeichen nicht ändert. Die bei $x_{2} = 4$ ist eine einfache, da sich das Vorzeichen ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da bei $- 2$ eine doppelte und bei $4$ eine einfache Nullstelle ist, muss in der Funktion $(x + 2)^{2} \cdot (x - 4)$ vorkommen. Das ist nur bei der Funktion $g$ der Fall.
Lösung: Der rote Graph gehört zu der Funktion $g$ .
Grüner Graph
Lies als Erstes die Nullstellen der Funktion ab.
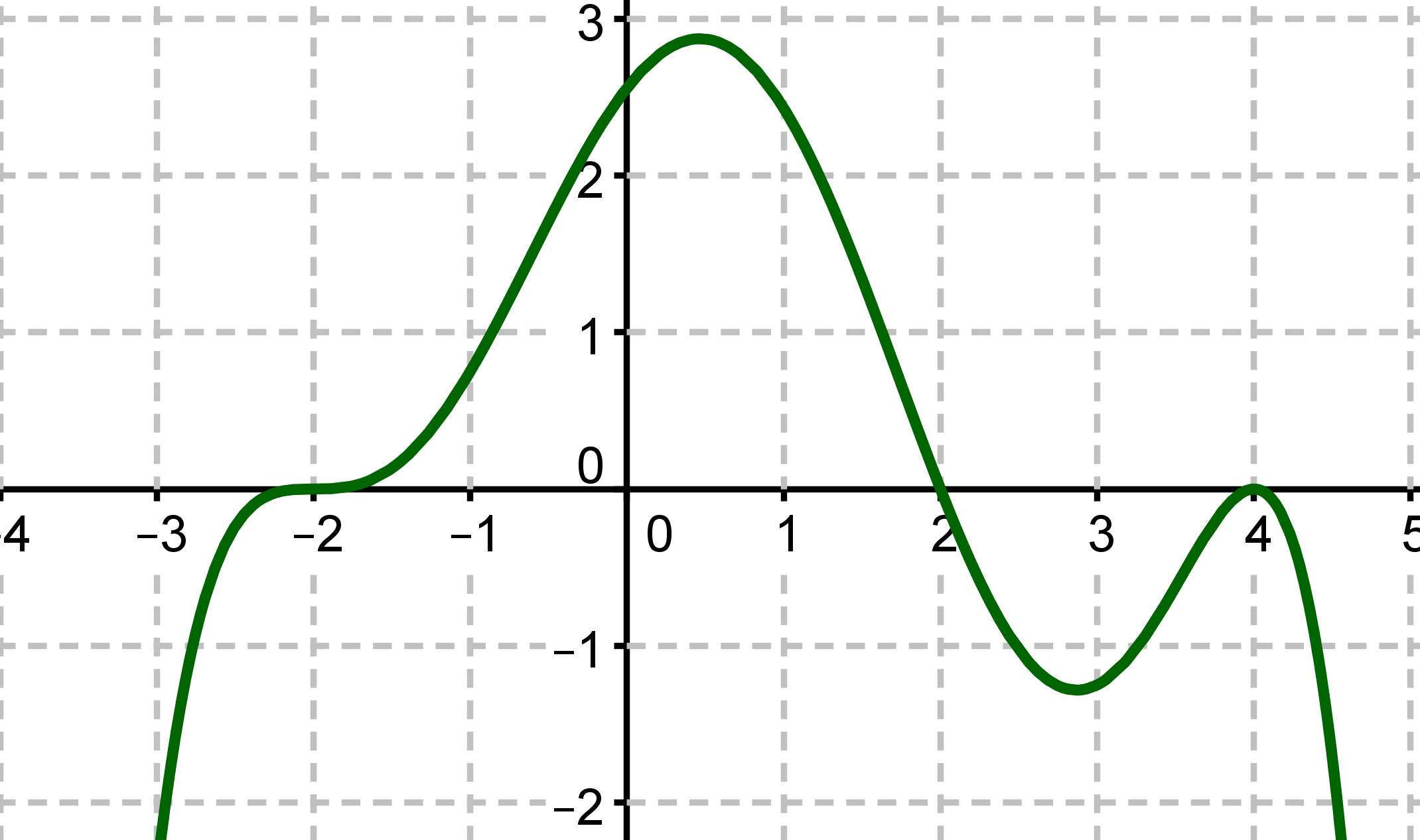
Die Nullstellen des grünen Graphen sind bei $x_{1} = - 2$ , $x_{2} = 2$ und $x_{3} = 4$ .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstelle bei $x_{1} = - 2$ ist eine dreifache Nullstelle, weil sich das Vorzeichen ändert und der Graph an der Stelle flach ist. Die bei $x_{2} = 2$ ist eine einfache, da sich das Vorzeichen ändert. Bei $x_{3} = 4$ ist es eine doppelte Nullstelle, weil sich das Vorzeichen nicht ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da bei $- 2$ eine dreifache, bei $2$ eine einfache und bei $4$ eine doppelte Nullstelle ist, muss in der Funktion $(x + 2)^{3} \cdot (x - 2) \cdot (x - 4)^{2}$ vorkommen. Das ist nur bei der Funktion $h$ der Fall.
Lösung: Der grüne Graph gehört zu der Funktion $h$ .
Lila Graph
Lies als Erstes die Nullstellen der Funktion ab.
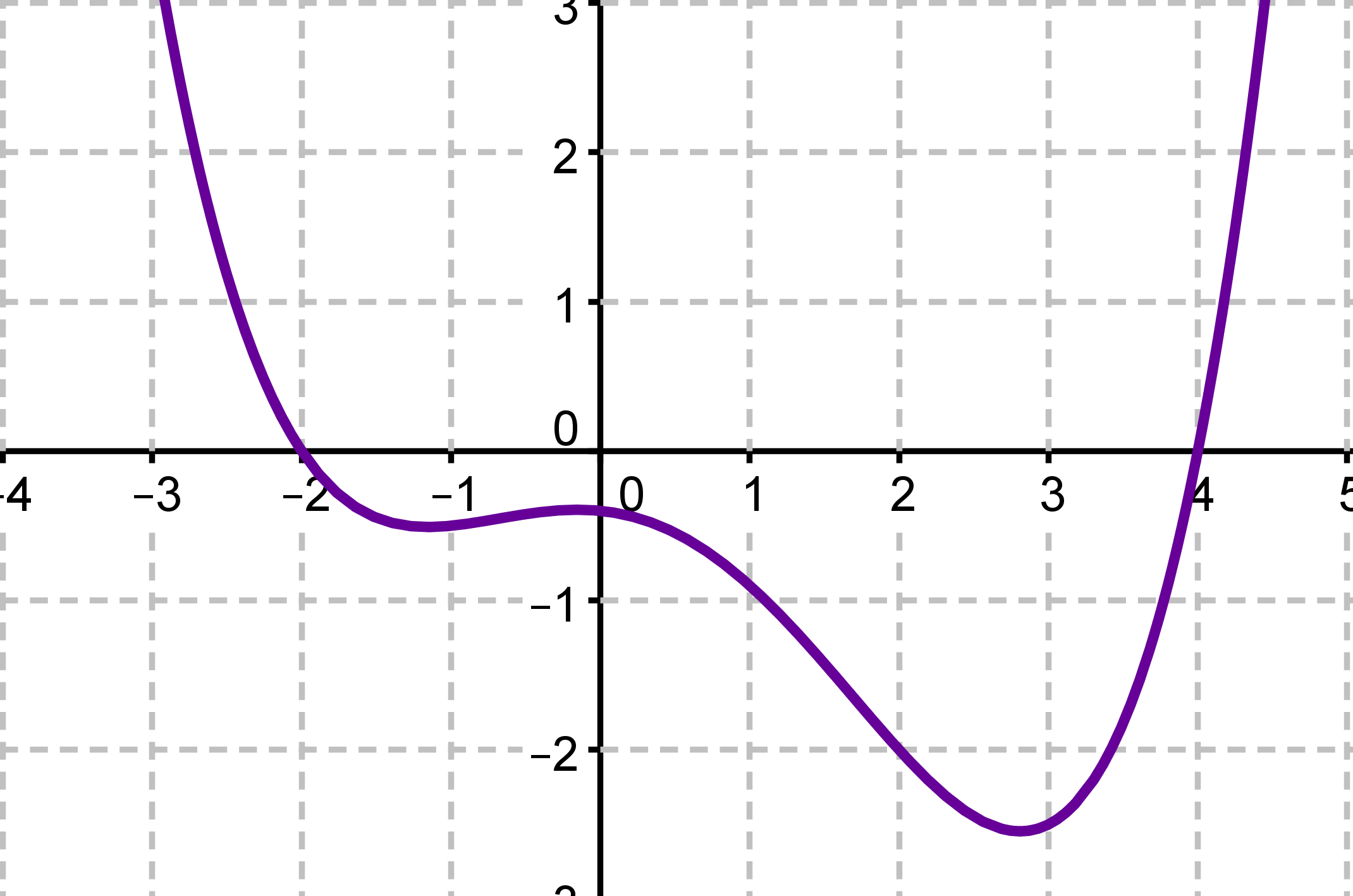
Die Nullstellen des roten Graphen sind bei $x_{1} = - 2$ und $x_{2} = 4$ .
Bestimme die Vielfachheiten der Nullstellen.
Die Nullstellen sind beides einfache Nullstellen, weil sich jedesmal das Vorzeichen ändert.
Gucke jetzt in den Funktionen nach allen verbleibenden Möglichkeiten. Da sowohl bei $2$ als auch bei $4$ eine einfache Nullstelle ist, muss in der Funktion $(x + 2) \cdot (x - 4)$ vorkommen. Das ist nur bei der Funktion $j$ der Fall.
Lösung: Der lila Graph gehört zu der Funktion $j$ .
6
Bestimme die Nullstelle(n) folgender Funktionen.
1. $f (x) = 4 x + 20$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  $f (x)$ $=$ $4 x + 20$
  ↓
  Setze f(x)=0
  $4 x + 20$ $=$ $0$ $- 20$
  $4 x$ $=$ $- 20$ $: 4$
  $x$ $=$ $- 5$
  Die Funktion hat eine Nullstelle bei $x = - 5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (x) = 14 x - 21$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  $f (x)$ $=$ $14 x - 21$
  ↓
  Setze f(x)=0
  $14 x - 21$ $=$ $0$ $+ 21$
  $14 x$ $=$ $21$ $: 14$
  $x$ $=$ $1,5$
  Die Funktion hat eine Nullstelle bei $x = 1,5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (x) = x^{2} + 6 x - 14$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  $f (x)$ $=$ $x^{2} + 6 x - 14 = 0$
  ↓
  mit der pq-Formel lösen.
  $x_{1,2}$ $=$ $- (\frac{p}{2}) \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
  Im obigen Fall ist p=6 und q=-14.
  Einsetzen in die Formel:
  $x_{1,2}$ $=$ $- 3 \pm \sqrt{9 - (- 14)}$
  $x_{1}$ $=$ $- 3 + \sqrt{23} \lor x_{2} = - 3 - \sqrt{23}$
  Die Nullstellen liegen also bei $x_{1} \approx 1,8$ und $x_{1} \approx - 7,8$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f (x) = x^{2} - 5 x + 6$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Lösung mit der Mitternachtsformel:
  $f (x)$ $=$ $x^{2} - 5 x + 6 = 0$
  ↓
  Bestimme die Koeffizienten a, b und c.
  $a$ $=$ $1$
  $b$ $=$ $- 5$
  $c$ $=$ $6$
  ↓
  Setze nun die 3 Koeffizienten in die Mitternachtsformel ein.
  $x_{1,2}$ $=$ $\frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 \cdot 1 \cdot 6}}{2 \cdot 1}$
  $=$ $\frac{5 \pm \sqrt{25 - 24}}{2}$
  $=$ $\frac{5 \pm 1}{2}$
  $x_{1}$ $=$ $3$
  $x_{2}$ $=$ $2$
  Die Funktion f hat also die Nullstellen $x_{1} = 3$ und $x_{2} = 2$ .
  Lösung mit dem Satz von Vieta:
  $x^{2} - 5 x + 6$ $=$ $0$
  ↓
  Da die Gleichung die Form $x^{2} + p x + q = 0$ hat, können wir den Satz von Vieta anwenden.
  $x_{1} + x_{2}$ $=$ $- p = - (- 5) = 5$
  $x_{1} \cdot x_{2}$ $=$ $q = 6$
  Versuche durch Raten Lösungen für $x_{1}$ und $x_{2}$ zu finden. Mögliche Kandidaten sind die Teiler von 6. Also 1,2,3 und 6.
  $x_{1}$
  $x_{2}$
  $x_{1} + x_{2}$
  $x_{1} \cdot x_{2}$
  $1$
  $6$
  $1 + 6 = 7$
  $1 \cdot 6 = 6$
  $2$
  $3$
  $2 + 3 = 5$
  $2 \cdot 3 = 6$
  Die Lösungen sind also $x_{1} = 2$ und $x_{2} = 3$ .
  Es ergeben sich die gleichen Ergebnisse wie bei der Mitternachtsformel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Bestimme die Nullstellen:
1. $f (x) = x^{4} - 3 x^{2} + 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x)$ $=$ $x^{4} - 3 x^{2} + 2$
  ↓
  f(x) gleich 0 setzen, um die Nullstellen zu bestimmen
  $x^{4} - 3 x^{2} + 2$ $=$ $0$
  Substitution
  Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. $u$ ) ersetzt.
  $u$ $=$ $x^{2}$
  $f (u)$ $=$ $u^{2} - 3 u + 2 = 0$
  ↓
  Mitternachtsformel anwenden
  $u_{1,2}$ $=$ $\frac{3 \pm \sqrt{{(- 3)}^{2} - 4 \cdot 1 \cdot 2}}{2 \cdot 1}$
  ↓
  Unter der Wurzel ausmultiplizieren.
  $=$ $\frac{3 \pm \sqrt{9 - 8}}{2}$
  ↓
  Wurzel ziehen.
  $=$ $\frac{3 \pm 1}{2}$
  $u_{1} : \frac{4}{2} = 2$
  Fall: +
  $u_{2} : \frac{2}{2} = 1$
  Fall: -
  Resubstitution
  Die Resubstitution beschreibt das Rückgängigmachen der Substitution.
  $x_{1,2}^{2}$ $=$ $2$
  ↓
  Wurzel ziehen
  $x_{1,2}$ $=$ $\pm \sqrt{2}$
  $x_{3,4}^{2}$ $=$ $1$
  ↓
  Wurzel ziehen
  $x_{3,4}$ $=$ $\pm 1$
  Die Nullstellen der Funktion lauten $x_{1} = \sqrt{2}, x_{2} = - \sqrt{2}, x_{3} = 1, x_{4} = - 1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (x) = x^{4} - \frac{17}{4} x^{2} + 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  Substitution
  Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. $u$ ) ersetzt.
  $u$ $=$ $x^{2}$
  $f (u)$ $=$ $u^{2} - \frac{17}{4} u + 1$
  ↓
  Mitternachtsformal anwenden
  $u_{1 / 2}$ $=$ $\frac{\frac{17}{4} \pm \sqrt{(- \frac{17}{4})^{2} - 4 \cdot 1 \cdot 1}}{2}$
  ↓
  Unter der Wurzel ausmultiplizieren
  $=$ $\frac{\frac{17}{4} \pm \sqrt{14,0625}}{2}$
  ↓
  Wurzel ziehen
  $=$ $\frac{\frac{17}{4} \pm \frac{15}{4}}{2}$
  $u_{1}$ $=$ $4$
  ↓
  Fall: +
  $u_{2}$ $=$ $\frac{1}{4}$
  ↓
  Fall: -
  Resubstitution
  Die Resubstitution beschreibt das Rückgängigmachen der Substitution.
  $x_{1,2}^{2}$ $=$ $4$
  ↓
  Wurzel ziehen
  $x_{1,2}$ $=$ $\pm 2$
  $x_{3,4}^{2}$ $=$ $\frac{1}{4}$
  ↓
  Wurzel ziehen
  $x_{3,4}$ $=$ $\pm \frac{1}{2}$
  Die Nullstellen der Funktion liegen bei $x_{1} = 2, x_{2} = - 2, x_{3} = \frac{1}{2}, x_{4} = - \frac{1}{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (x) = (x^{2} - \frac{3}{2})^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x)$ $=$ $(x^{2} - \frac{3}{2})^{2}$
  Substitution
  Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. $u$ ) ersetzt.
  $u$ $=$ $x^{2}$
  $f (u)$ $=$ $(u - \frac{3}{2})^{2} = (u - \frac{3}{2}) (u - \frac{3}{2})$
  ↓
  Die Nullstellen können abgelesen werden
  $u$ $=$ $\frac{3}{2}$
  ↓
  Doppelte Nullstelle
  Resubstitution
  Die Resubstitution beschreibt das Rückgängigmachen der Substitution.
  $x_{1,2}^{2}$ $=$ $\frac{3}{2}$
  ↓
  Wuzel ziehen
  $x_{1}$ $=$ $\sqrt{\frac{3}{2}}$
  $x_{2}$ $=$ $- \sqrt{\frac{3}{2}}$
  ↓
  Zwei doppelte Nullstellen
  Die Funktion hat zwei doppelte Nullstellen und zwar bei $x_{1} = \sqrt{\frac{3}{2}}$ und $x_{2} = - \sqrt{\frac{3}{2}}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f (x) = \frac{1}{2} x^{6} - 2 x^{3} - 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x)$ $=$ $\frac{1}{2} x^{6} - 2 x^{3} - 2$
  Substitution
  Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. $u$ ) ersetzt.
  $u$ $=$ $x^{3}$
  $f (u)$ $=$ $\frac{1}{2} u^{2} - 2 u - 2$
  ↓
  Mitternachtsformel anwenden
  $u_{1,2}$ $=$ $\frac{2 \pm \sqrt{(- 2)^{2} - 4 \cdot \frac{1}{2} \cdot (- 2)}}{2 \cdot \frac{1}{2}}$
  $=$ $\frac{2 \pm \sqrt{8}}{1} = 2 \pm \sqrt{8}$
  $u_{1}$ $=$ $2 + \sqrt{8} \approx 4,83$
  ↓
  Fall: +
  $u_{2}$ $=$ $2 - \sqrt{8} \approx - 0,83$
  ↓
  Fall: -
  Resubstitution
  Die Resubstitution beschreibt das Rückgängigmachen der Substitution.
  $x_{1}^{3}$ $\approx$ $4,83$
  ↓
  dritte Wurzel ziehen
  $x_{1}$ $\approx$ $\sqrt[3]{4,83} \approx 1,69$
  $x_{2}^{3}$ $\approx$ $- 0,83$
  ↓
  dritte Wurzel ziehen
  $x_{2}$ $\approx$ $\sqrt[3]{- 0,83} \approx - 0,94$
  Die Funktion hat 2 Nullstellen bei $x_{1} \approx \sqrt[3]{4,83} \approx 1,69$ und bei $x_{2} \approx \sqrt[3]{- 0,83} \approx - 0,94$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8
Berechne die Nullstellen der folgenden Funktion.
1. $f (x) = x^{3} + 3 x^{2} - 4 x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x)$ $=$ $x^{3} + 3 x^{2} - 4 x$
  ↓
  Setze die Funktion gleich 0.
  $0$ $=$ $x^{3} + 3 x^{2} - 4 x$
  ↓
  Klammere $x$ aus.
  $0$ $=$ $x (x^{2} + 3 x - 4)$
  Ein Produkt ist dann gleich 0, wenn einer der Faktoren 0 ist, du erhältst also die erste Nullstelle:
  $x_{1} = 0$
  Die anderen Nullstellen erhältst du, wenn du den zweiten Faktor gleich 0 setzt:
  $(x^{2} + 3 x - 4) = 0$
  Wende nun die Mitternachtsformel an, um das Ergebnis zu erhalten:
  $x_{2,3} = \frac{- 3 \pm \sqrt{3^{2} - 4 \cdot 1 \cdot (- 4)}}{2 \cdot 1}$
  $x_{2,3}$ $=$ $\frac{- 3 \pm \sqrt{3^{2} - 4 \cdot 1 \cdot (- 4)}}{2 \cdot 1}$
  ↓
  Fasse unter der Wurzel zusammen.
  $=$ $\frac{- 3 \pm \sqrt{9 + 16}}{2}$
  $=$ $\frac{- 3 \pm \sqrt{25}}{2}$
  ↓
  Ziehe die Wurzel
  $=$ $\frac{- 3 \pm 5}{2}$
  Du erhältst also die beiden Nullstellen:
  $x_{2} = \frac{- 3 + 5}{2} = 1$
  und:
  $x_{3} = \frac{- 3 - 5}{2} = - 4$
  Die Funktion hat also insgesamt 3 Nullstellen und zwar bei $x_{1} = 0, x_{2} = 1$ und $x_{3} = - 4$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $f (x) = x^{4} + 2 x^{3} + x^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x)$ $=$ $x^{4} + 2 x^{3} + x^{2}$
  ↓
  Klammere die kleinste Potenz von $x$ aus und setze $f (x)$ = 0
  $0$ $=$ $x^{2} \cdot (x^{2} + 2 x + 1)$
  Ein Produkt ist dann gleich 0, wenn einer der Faktoren 0 ist, du erhältst also die erste Nullstelle:
  $x_{1} = 0$
  Das ist eine doppelte Nullstelle, da $x^{2}$ in der Faktordarstellung vorkommt.
  Die anderen Nullstellen erhältst du, wenn du den zweiten Faktor gleich 0 setzt:
  $(x^{2} + 2 x + 1) = 0$
  Wenn du die 1. binomische Formel anwendest, erhältst du:
  ${(x + 1)}^{2} = 0$
  $x_{2} = - 1$ ist also auch eine doppelte Nullstelle.
  Die Funktion hat also 2 doppelte Nullstellen und zwar bei $x_{1} = 0$ und $x_{2} = - 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $f (x) = (x^{2} - 25) \cdot (\frac{1}{2} x + 4)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x) = (x^{2} - 25) \cdot (\frac{1}{2} x + 4)$
  Setze die Funktion gleich 0:
  $0 = (x^{2} - 25) \cdot (\frac{1}{2} x + 4)$
  Ein Produkt ist dann gleich 0, wenn einer der Faktoren 0 ist, setze nun die erste Klammer gleich 0:
  $0$ $=$ $(x^{2} - 25)$
  ↓
  Benutze die 3. Binomische Formel
  $0$ $=$ $(x - 5) \cdot (x + 5)$
  $\Rightarrow x_{1,2} = \pm 5$
  Setze als nächstes die zweite Klammer $0$ .
  $0$ $=$ $\frac{1}{2} x + 4$ $- 4$
  $- 4$ $=$ $\frac{1}{2} x$ $\cdot 2$
  $- 8$ $=$ $x$
  $\Rightarrow x_{3} = - 8$
  Die Funktion hat also 3 Nullstellen und zwar bei $x_{1} = 5, x_{2} = - 5$ und $x_{3} = - 8$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $f (x) = x^{2} - 6 x + 9$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x)$ $=$ $x^{2} - 6 x + 9$
  ↓
  Setze die Funktion gleich 0.
  $0$ $=$ $x^{2} - 6 x + 9$
  ↓
  Wende die 2. Binomische Formel an.
  $0$ $=$ ${(x - 3)}^{2}$
  $0$ $=$ $(x - 3) \cdot (x - 3)$
  Die Funktion hat also eine doppelte Nullstelle bei $x = 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $f (x) = x^{6} - x^{4}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x)$ $=$ $x^{6} - x^{4}$
  ↓
  Setze die Funktion gleich 0.
  $0$ $=$ $x^{6} - x^{4}$
  ↓
  Klammere die kleinste Potenz von $x$ aus.
  $0$ $=$ $x^{4} \cdot (x^{2} - 1)$
  Ein Produkt ist dann gleich 0, wenn einer der Faktoren 0 ist, du erhältst also die erste Nullstelle:
  $x_{1} = 0$
  Das ist eine vierfache Nullstelle, da $x^{4}$ in der Faktordarstellung vorkommt.
  Die anderen Nullstellen erhältst du, wenn du den zweiten Faktor gleich 0 setzt:
  $0$ $=$ $(x^{2} - 1)$
  ↓
  Verwende die 3. Binomische Formel.
  $0$ $=$ $(x - 1) \cdot (x + 1)$
  $\Rightarrow x_{2,3} = \pm 1$
  Die Funktion hat also eine vierfache Nullstelle bei $x_{1} = 0$ und jeweils eine einfache Nullstelle bei $x_{2} = 1$ und $x_{3} = - 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $f (x) = x^{4} - 6 x^{2} + 5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x) = x^{4} - 6 x^{2} + 5$
  Diese Funktion ist ein Polynom 4. Grades, bei dem du $x$ nicht mehr ausklammern kannst, das macht es schwer die Nullstellen zu bestimmen. Hier verwendest du am besten eine Substitution:
  Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. $u$ ) ersetzt.
  $u = x^{2}$
  $f (x)$ $=$ $u^{2} - 6 u + 5$
  ↓
  Setze die Funktion gleich 0.
  $0$ $=$ $u^{2} - 6 u + 5$
  Hier kannst du jetzt die Mitternachtsformel anwenden:
  $u_{1,2}$ $=$ $\frac{6 \pm \sqrt{(- 6)^{2} - 4 \cdot 1 \cdot 5}}{2 \cdot 1}$
  ↓
  Fasse unter der Wurzel zusammen.
  $=$ $\frac{6 \pm \sqrt{36 - 20}}{2}$
  $=$ $\frac{6 \pm \sqrt{16}}{2}$
  $=$ $\frac{6 \pm 4}{2}$
  Du erhältst also die beiden Nullstellen:
  $u_{1} = \frac{6 + 4}{2} = 5$ und:
  $u_{2} = \frac{6 - 4}{2} = 1$
  Resubstitution
  Die Resubstitution beschreibt das Rückgängigmachen der Substitution.
  $x_{1,2}^{2}$ $=$ $u_{1}$
  $x_{1,2}^{2}$ $=$ $5$ $\sqrt{}$
  $x_{1,2}$ $=$ $\pm \sqrt{5}$
  Und noch für $u_{2}$ :
  $x_{3,4}^{2}$ $=$ $u_{2}$
  $x_{3,4}^{2}$ $=$ $1$ $\sqrt{}$
  $x_{3,4}$ $=$ $\pm 1$
  Die Funktion hat also 4 Nullstellen und zwar bei $x_{1} = \sqrt{5}, x_{2} = - \sqrt{5}, x_{3} = 1$ und $x_{4} = - 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. $f (x) = (2 x - 4) (4 x^{2} - \frac{1}{3} x + 2) - 4 x + 8$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x) = (2 x - 4) (4 x^{2} - \frac{1}{3} x + 2) - 4 x + 8$
  Ersetze den "schlimmen Teil"
  Den Term $(4 x^{2} - \frac{1}{3} x + 2)$ bezeichnen wir als "schlimmen Teil". Ersetzen wir ihn also auch in der Vorschrift von $f$ :
  $f (x) = (2 x - 4) \cdot$ schlimmer Teil $- 4 x + 8$
  Was haben die Terme $(2 x - 4)$ und $- 4 x + 8$ gemeinsam?
  $- 4 x + 8 = (- 2) \cdot (2 x - 4)$
  Setze dies in die Vorschrift von $f$ ein
  $f (x) = (2 x - 4) \cdot$ schlimmer Teil $- 2 \cdot (2 x - 4)$
  Klammere $(2 x - 4)$ aus
  $f (x) = (2 x - 4) \cdot$ $($ schlimmer Teil $- 2)$
  Setze den "schlimmen Teil" ein
  $f (x) = (2 x - 4) \cdot ((4 x^{2} - \frac{1}{3} x + 2) - 2)$
  Löse innere Klammer auf
  $f (x) = (2 x - 4) \cdot (4 x^{2} - \frac{1}{3} x + 2 - 2)$
  $- 2$ und $+ 2$ heben sich gegenseitig auf
  $f (x) = (2 x - 4) \cdot (4 x^{2} - \frac{1}{3} x)$
  $f$ ist das Produkt von zwei Polynomfunktionen. Berechne die Nullstellen der Faktoren.
  Nullstellen des linken Faktors
  Setze $(2 x - 4)$ gleich Null
  $2 x - 4 = 0$
  Bringe die $4$ auf die andere Seite
  $2 x - 4 = 0 | + 4$
  Teile durch $2$
  $2 x = 4 | : 2$
  Erhalte die Nullstelle
  $x_{1} = 2$
  Nullstellen des rechten Faktors
  Setze $(4 x^{2} - \frac{1}{3} x)$ gleich null. Da hier kein konstantes Glied auftaucht, können wir die kleinste Potenz von $x$ ausklammern. Wir haben dann: $x \cdot (4 x - \frac{1}{3})$
  Dort lesen wir die Nullstelle $x_{2} = 0$ ab. Es fehlen uns nur noch die Nullstellen von $(4 x - \frac{1}{3})$ . Diese berechnen wir, indem wir $4 x - \frac{1}{3}$ gleich null setzen und diese Gleichung nach $x$ auflösen.
  $4 x - \frac{1}{3} = 0$
  Bringe die $\frac{1}{3}$ auf die andere Seite
  $4 x - \frac{1}{3} = 0 | + \frac{1}{3}$
  Teile durch 4
  $4 x = \frac{1}{3} | : 4$
  Erhalte die Nullstelle
  $x_{3} = \frac{1}{12}$
  Und die Nullstellen von $f$ lauten…
  Das war etwas mühsam. Doch jetzt haben wir alle Nullstellen von $f$ . Sie lauten $x_{1} = 2, x_{2} = 0$ und $x_{3} = \frac{1}{12}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Tipp: Welcher Teil bereitet dir Probleme? Kannst du ihn "ignorieren"?
  Wenn du völlig auf dem Schlauch stehst, gehe nochmal zurück auf die Seite 2. Ausklammern von Faktoren(2|2).
8. $f (x) = x^{3} + 2 x^{2} - 5 x - 6$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x) = x^{3} + 2 x^{2} - 5 x - 6$
  Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $1$ in $f (x)$ ein.
  $f (1) = 1^{3} + 2 \cdot 1^{2} - 5 \cdot 1 - 6 = - 8$
  $f (1) \neq 0$
  Setze als nächstes z.B. $- 1$ in $f (x)$ ein.
  $f (- 1) = (- 1)^{3} + 2 \cdot (- 1)^{2} - 5 \cdot (- 1) - 6 = 0$
  Die Funktion $f (x)$ hat an der Stelle $x_{1} = - 1$ eine Nullstelle. Da $f (- 1) = 0$ , wissen wir, dass $f (x)$ den dazugehörigen Linearfaktor $(x + 1)$ besitzt.
  Führe nun die Polynomdivision $f (x) : (x + 1)$ durch.
  $\begin{matrix} (x^{3} + 2 x^{2} - 5 x - 6) : (x + 1) = x^{2} + x - 6 \\ - (x^{3} + x^{2}) \\ x^{2} - 5 x \\ - (x^{2} + x) \\ - 6 x - 6 \\ - (- 6 x - 6) \\ 0 \end{matrix}$
  Die Funktion $f (x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_{1} = - 1$ bereits bekannt ist, kannst du die weiteren Nullstellen von $f$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.
  $x^{2} + x - 6 = 0$
  Wende hier die Mitternachtsformel an.
  $x_{2,3}$ $=$ $\frac{- 1 \pm \sqrt{1^{2} - 4 \cdot 1 \cdot (- 6)}}{2 \cdot 1}$
  ↓
  Fasse unter der Wurzel zusammen
  $=$ $\frac{- 1 \pm \sqrt{25}}{2 \cdot 1}$
  $=$ $\frac{- 1 \pm 5}{2 \cdot 1}$
  Du erhältst die beiden Nullstellen:
  $x_{2} = \frac{4}{2} = 2$ und:
  $x_{3} = \frac{- 6}{2} = - 3$
  Die Funktion $f (x)$ hat also drei Nullstellen bei $x_{1} = - 1$ , $x_{2} = 2$ und $x_{3} = - 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
Bestimme mithilfe der Substitutionsmethode die Nullstellen von f.
1. $f (x) = x^{4} - 2 x^{2} - 8$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Substitutionsverfahren
  $f (x) = x^{4} - 2 x^{2} - 8$
  Setze die Gleichung gleich $0$ .
  $0 = x^{4} - 2 x^{2} - 8$
  Nun zur Substitution:
  $0 = (x^{2})^{2} - 2 x^{2} - 8$
  Substituiere: $z = x^{2}$ .
  $0 = z^{2} - 2 z - 8$
  Löse die so gewonnene Gleichung mit Hilfe der Mitternachtsformel.
  $z_{1,2} = \frac{2 \pm \sqrt{2^{2} - 4 \cdot 1 \cdot (- 8)}}{2 \cdot 1}$
  Jetzt wird noch vereinfacht.
  $z_{1,2} = \frac{2 \pm \sqrt{36}}{2}$
  $z_{1} = \frac{2 + 6}{2} = 4$
  $z_{2} = \frac{2 - 6}{2} = - 2$
  Zum Schluss muss natürlich die Resubstitution angewandt:
  Um auf die Nullstellen von $f (x)$ zu kommen, musst du nun noch resubstituieren:
  $z = x^{2} \Leftrightarrow x = \pm \sqrt{z}$
  Aus $z_{1} = 4$ folgt:
  $x_{1,2} = \pm \sqrt{4} \Rightarrow x_{1} = 2$ und $x_{2} = - 2$
  Aus $z = - 2$ bekommt man keine Lösungen für $f (x) = 0$ , da man aus um auf $x$ zu kommen die Wurzel aus $- 2$ ziehen müsste. Aber man kann keine Quadratwurzeln aus negativen Zahlen ziehen!
  Die Funktion hat also die beiden Nullstellen $x_{1} = 2$ und $x_{2} = - 2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (x) = \frac{1}{2} x^{6} + x^{3} - 4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Substitutionsverfahren
  $f (x) = \frac{1}{2} x^{6} + x^{3} - 4$
  Setzte die Gleichung gleich $0$ .
  $0 = \frac{1}{2} x^{6} + x^{3} - 4$
  Nun zur Substitution:
  $0 = \frac{1}{2} (x^{3})^{2} + x^{3} - 4$
  Substituiere: $u = x^{3}$ .
  $0 = \frac{1}{2} u^{2} + u - 4$
  Wende nun die Mitternachtsformel an um die Nullstellen der substituierten Gleichung zu berechnen.
  $u_{1,2} = \frac{- 1 \pm \sqrt{1^{2} - 4 \cdot \frac{1}{2} \cdot (- 4)}}{2 \cdot \frac{1}{2}}$
  Jetzt wird noch vereinfacht.
  $u_{1,2} = \frac{- 1 \pm \sqrt{1 + 8}}{1}$
  $u_{1,2} = - 1 \pm \sqrt{9}$
  $u_{1,2} = - 1 \pm 3$
  Berechne $u_{1}$ und $u_{2}$ .
  $u_{1} = 2$ und $u_{2} = - 4$
  Resubstitution
  Um auf die Nullstellen von $f (x)$ zu kommen, musst du nun noch resubstituieren:
  $u = x^{3} \Leftrightarrow x = \sqrt[3]{u}$
  $u_{1} = 2 \Leftrightarrow x_{1} = \sqrt[3]{2} \approx 1,26$
  $u_{2} = - 4 \Leftrightarrow x_{2} = \sqrt[3]{- 4} \approx - 1,59$
  Die Funktion hat also die beiden Nullstellen $x_{1} = \sqrt[3]{2}$ und $x_{2} = \sqrt[3]{- 4}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

$x_{1}$	$x_{2}$	$x_{1} + x_{2}$	$x_{1} \cdot x_{2}$
$1$	$6$	$1 + 6 = 7$	$1 \cdot 6 = 6$
$2$	$3$	$2 + 3 = 5$	$2 \cdot 3 = 6$

Berechne die Nullstellen folgender Funktionen.

$f (x) = \frac{1}{4} x^{5} - 3 x^{3} + 8 x$

$g (x) = x^{7} - 7 x^{4} - 8 x$

$h (u) = u^{5} - 13 u^{3} + 36 u$

$k (z) = 2 z^{7} + 14 z^{4} - 16 z$

11
Finde und begründe den Fehler bei den folgenden Nullstellenbestimmungen.
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen bestimmen
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x) = x^{4} - 6 x^{2} + 8$
  Man wollte mithilfe der Substitution und des Satzes von Vieta die Nullstellen von $f (x)$ bestimmen.
  Dabei wurde sowohl die Substitution als auch der Satz von Vieta richtig angewandt.
  Die angegebenen Nullstellen $2$ und $4$ sind allerdings nicht die Nullstellen von $f (x)$ , sondern die Nullstellen der substituierten Funktion $f (u) = u^{2} - 6 u + 8$ .
  Grund: Es wurde nicht resubstituiert. Da nämlich $x^{2} = u$ gilt, muss für die Lösung der Nullstellen noch die Wurzel aus $2$ und $4$ gezogen werden.
  Somit hat $f (x)$ eigentlich die vier Nullstellen:
  $x_{1,2} = \pm \sqrt{2}$
  $x_{3,4} = \pm \sqrt{4} = \pm 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen bestimmen
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $g (x) = x^{4} - 12 x^{2} + 27$
  Man wollte mithilfe der Substitution und der Mitternachtsformel die Nullstellen von $g (x)$ bestimmen.
  Dabei wurde sowohl die Substitution als auch die Mitternachtsformel richtig angewandt.
  Jedoch sind die angegebenen Nullstellen zu wenige.
  Grund: Bei der Resubstitution werden $s_{1}$ sowie $s_{2}$ radiziert. Dabei kann die Lösung sowohl negativ als auch positiv sein.
  Somit hat $g (x)$ eigentlich die vier Nullstellen:
  $x_{1,2} = \pm \sqrt{9} = \pm 3$
  $x_{3,4} = \pm \sqrt{3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Begründe mithilfe des Substitutionsverfahrens, warum die Funktion $f (x) = x^{4} - 8 x^{2} - 9$ nur zwei Nullstellen besitzt.

Berechne die Nullstellen und entscheide welche Besonderheit vorliegt.

$f (x) = - \frac{1}{2} x^{3} - 2 x^{2}$

$f (x) = 2 x^{5} + 64$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
Nullstellenbestimmung
Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
$f (x)$ $=$ $2 x^{5} + 64$
↓
Die Funktion gleich 0 setzen
$0$ $=$ $2 x^{5} + 64$ $- 64$
$- 64$ $=$ $2 x^{5}$ $: 2$
$- 32$ $=$ $x^{5}$
↓
Fünfte Wurzel ziehen.
$x$ $=$ $- 2$
Die Funktion $f (x)$ hat eine Nullstelle bei $x = - 2$ .
Besonderheit
Spezialfall: alle Zwischenglieder fehlen
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = 3 x^{4} - 7 x^{2} + 2$

$f (x) = - \frac{1}{2} x^{4} - \frac{7}{2} x^{2} + 6$

$f (x) = \frac{1}{2} x^{4} - 8$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
Nullstellenbestimmung
Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
$f (x)$ $=$ $\frac{1}{2} x^{4} - 8$
↓
Die Funktion gleich 0 setzen
$0$ $=$ $\frac{1}{2} x^{4} - 8$ $+ 8$
$8$ $=$ $\frac{1}{2} x^{4}$ $\cdot 2$
$16$ $=$ $x^{4}$
↓
Vierte Wurzel ziehen.
$x_{1,2}$ $=$ $\pm 2$
Die Funktion hat die beiden Nullstellen $x_{1} = 2$ und $x_{2} = - 2$ .
Besonderheit
Spezialfall: alle Zwischenglieder fehlen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = x^{4} + 10 x^{3} + 25 x^{2}$

$f (x) = \frac{1}{2} x^{3} - \frac{1}{4} x$

$f (x) = - \frac{1}{4} x^{3} - 16$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen bestimmen
Nullstellenbestimmung
Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
$f (x)$ $=$ $- \frac{1}{4} x^{3} - 16$
↓
Funktion gleich 0 setzen
$0$ $=$ $- \frac{1}{4} x^{3} - 16$ $+ 16$
$16$ $=$ $- \frac{1}{4} x^{3}$ $: (- \frac{1}{4}) o d e r \cdot (- 4)$
↓
Brüche multiplizieren und dividieren
$- 64$ $=$ $x^{3}$ $\sqrt[3]{}$
↓
Dritte Wurzel ziehen
$x$ $=$ $- 4$
Die Funktion hat eine Nullstelle bei $x = - 4$ .
Besonderheit
Spezialfall: Alle Zwischenglieder fehlen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = 2 x^{5} - 5 x^{4} - 3 x^{3}$

$f (x) = x^{4} - 5 x^{2} + 4$

14
Bestimme die Nullstelle(n) der folgenden Funktion und gib die Linearfaktordarstellung von $f$ an:
$f : x \mapsto \frac{1}{6} x^{4} - \frac{1}{6} x^{3} - x^{2}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
Nullstellen bestimmen und Linearfaktordarstellung angeben.
$f (x) = \frac{1}{6} x^{4} - \frac{1}{6} x^{3} - x^{2}$
Zur Berechnung der Nullstellen setzt du als Erstes $f (x) = 0$ .
$\frac{1}{6} x^{4} - \frac{1}{6} x^{3} - x^{2} = 0$
Aus dieser Gleichung klammerst du am Besten $x^{2}$ aus.
$x^{2} \cdot (\frac{1}{6} x^{2} - \frac{1}{6} x - 1) = 0$
Damit ist nämlich ein Produkt entstanden, das gleich $0$ ist. Daher kannst du nun jeden der Faktoren einzeln gleich $0$ setzen.
$\Rightarrow x^{2} = 0$ oder $\frac{1}{6} x^{2} - \frac{1}{6} x - 1 = 0$
$x^{2} = 0 \Rightarrow x = 0$ . Das ergibt die Nullstelle: $x_{1} = 0$
$\frac{1}{6} x^{2} - \frac{1}{6} x - 1 = 0 \Rightarrow ?$ Die Nullstellen des Terms in der Klammer musst du noch bestimmen.
$\frac{1}{6} x^{2} - \frac{1}{6} x - 1 = 0$
Das ist eine quadratische Gleichung, und darauf kannst du die Lösungsformel anwenden.
Das kannst du entweder jetzt direkt gleich tun;
oder du multiplizierst vorher, wenn du geschickt vorgehen möchtest, die Gleichung erst mit $6$ .
Dann fallen nämlich alle Brüche weg!
$\frac{1}{6} x^{2} - \frac{1}{6} x - 1 = 0$ | $\cdot 6$
$x^{2} - x - 6 = 0$
Berechne hiervon die Diskriminante.
$D = (- 1)^{2} - 4 \cdot 1 \cdot (- 6) = 25$
Die Diskriminante ist größer als $0$ , also kannst du weiterrechnen und die beiden Lösungen bestimmen.
$x_{2 / 3} = \frac{- (- 1) \pm \sqrt{25}}{2 \cdot 1}$
Die Lösungen heißen hier $x_{2 / 3}$ statt $x_{1 / 2}$ , da die Bezeichnung $x_{1}$ ja schon für die Nullstelle $x_{1} = 0$ vergeben wurde.
$x_{2 / 3} = \frac{1 \pm 5}{2}$
Rechne beide Werte aus.
$x_{2} = \frac{1 + 5}{2} = \frac{6}{2} = 3$
$x_{3} = \frac{1 - 5}{2} = \frac{- 4}{2} = - 2$
Jetzt hast du alle Nullstellen von $f$ erhalten und kannst auch ihre Vielfachheiten angeben.
Nullstellen von $f$ :
$x_{1} = 0$
doppelte Nullstelle, d.h. Vielfachheit 2
$x_{2} = 3$
einfache Nullstelle, d.h. Vielfachheit 1
$x_{3} = - 2$
einfache Nullstelle, d.h. Vielfachheit 1
Linearfaktordarstellung angeben
$f (x) = ?$
Um die Linearfaktordarstellung angeben zu können, brauchst du
alle Nullstellen der Funktion, und
deren Vielfachheiten;
und den Faktor, der in der Funktion vor der höchsten $x$ -Potenz steht.
Als Linearfaktordarstellung von $f$ ergibt sich:
$f (x) = \frac{1}{6} \cdot (x - 0)^{2} \cdot (x - 3) \cdot (x - (- 2))$
oder kürzer $f (x) = \frac{1}{6} x^{2} (x - 3) (x + 2)$

Bestimme die Nullstellen der Funktionen, indem du faktorisierst.

$f (x) = 3 x^{4} - 9 x^{3}$

$f (x) = 2 x^{3} - x$

$f (x) = 3 x^{3} - 3 x^{2} - 6 x$

$f (x) = x^{2} - 81$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
Es gibt (mindestens) drei Möglichkeiten:
Wurzelziehen
$\begin{aligned} f (x) = 0 & ⟺ x^{2} - 81 = 0 \\ ⟺ x^{2} = 81 \\ ⟺ x = 9 \lor x = - 9 \end{aligned}$
Dritte binomische Formel
$\begin{aligned} f (x) = 0 & ⟺ x^{2} - 81 = 0 \\ ⟺ (x + 9) \cdot (x - 9) = 0 \end{aligned}$
Nach dem Satz vom Nullprodukt folgt
$x + 9 = 0 \lor x - 9 = 0 ⟺ x = - 9 \lor x = 9$ .
Mitternachtsformel
Um diese Gleichung lösen zu können, brauchst du Wissen über die Mitternachtsformel.
Bestimme die Nullstellen:
$f (x)$ $=$ $x^{2} - 81$
↓
Setze die Gleichung in die Mitternachtsformel ein.
$x_{1,2}$ $=$ $\frac{- 0 \pm \sqrt{0^{2} - 4 \cdot 1 \cdot (- 81)}}{2 \cdot 1}$
↓
Löse den Inhalt der Diskriminante.
$x_{1,2}$ $=$ $\frac{- 0 \pm \sqrt{324}}{2}$
Fall 1:+
$x_{1} = \frac{+ 18}{2} = 9$
Fall 2:-
$x_{2} = \frac{- 18}{2} = - 9$
Ergebnis:
Die Funktion hat die beiden Nullstellen $x_{1} = 9$ und $x_{2} = - 9$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = x^{2} - 10 x + 25$

$f (x) = 9 x^{2} + 24 x + 16$

$f (x) = 9 x^{4} - 81 x^{2}$

16
Berechne die Nullstellen folgender Funktionen mithilfe der Polynomdivision.
1. $f (x) = x^{3} - x^{2} - 4 x + 4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f (x) = x^{3} - x^{2} - 4 x + 4$
  Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $1$ in $f (x)$ ein.
  $f (1) = 1^{3} - 1^{2} - 4 \cdot 1 + 4 = 0$
  Die Funktion $f (x)$ hat an der Stelle $x_{1} = 1$ eine Nullstelle. Da $f (1) = 0$ , wissen wir, dass $f (x)$ den dazugehörigen Linearfaktor $(x - 1)$ besitzt.
  Führe nun die Polynomdivision $f (x) : (x - 1)$ durch.
  $\begin{matrix} (x^{3} - x^{2} - 4 x + 4) : (x - 1) = x^{2} - 4 \\ - (x^{3} - x^{2}) \\ 0 - 4 x + 4 \\ - (- 4 x + 4) \\ 0 \end{matrix}$
  Die Funktion $f (x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_{1} = 1$ bereits bekannt ist, kannst du die weiteren Nullstellen von $f$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.
  $x^{2} - 4$ $=$ $0$ $+ 4$
  $x^{2}$ $=$ $4$
  ↓
  Wurzel ziehen.
  $x_{2,3}$ $=$ $\pm \sqrt{4}$
  $=$ $\pm 2$
  Die Funktion $f (x)$ hat drei Nullstellen bei $x_{1} = 1$ , $x_{2} = 2$ und $x_{3} = - 2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $g (x) = x^{3} + 3 x^{2} - 16 x + 12$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $g (x) = x^{3} + 3 x^{2} - 16 x + 12$
  Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $1$ in $g (x)$ ein.
  $g (1) = 1^{3} + 3 \cdot 1^{2} - 16 \cdot 1 + 12 = 0$
  Die Funktion $g (x)$ hat an der Stelle $x_{1} = 1$ eine Nullstelle. Da $g (1) = 0$ , wissen wir, dass $g (x)$ den dazugehörigen Linearfaktor $(x - 1)$ besitzt.
  Führe nun die Polynomdivision $g (x) : (x - 1)$ durch.
  $\begin{matrix} - (x^{3} + 3 x^{2} - 16 x + 12) : (x - 1) = x^{2} + 4 x - 12 \\ - (x^{3} - x^{2}) \\ 4 x^{2} - 16 x \\ - (4 x^{2} - 4 x) \\ - 12 x + 12 \\ - (- 12 x + 12) \\ 0 \end{matrix}$
  Die Funktion $g (x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_{1} = 1$ bereits bekannt ist, kannst du die weiteren Nullstellen von $g$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.
  $x^{2} + 4 x - 12$ $=$ $0$
  ↓
  Mitternachtsformel anwenden.
  $x_{2,3}$ $=$ $\frac{- 4 \pm \sqrt{4^{2} - 4 \cdot 1 \cdot (- 12)}}{2 \cdot 1}$
  ↓
  Unter der Wurzel zusammenfassen.
  $x_{2,3}$ $=$ $\frac{- 4 \pm \sqrt{64}}{2}$
  $=$ $\frac{- 4 \pm 8}{2}$
  $x_{2} = \frac{4}{2} = 2$
  $x_{3} = \frac{- 12}{2} = - 6$
  Fall 1: $+$
  Fall 2: $-$
  Die Funktion $g (x)$ hat drei Nullstellen bei $x_{1} = 1$ , $x_{2} = 2$ und $x_{3} = - 6$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $h (x) = 3 x^{4} + 12 x^{3} - 33 x^{2} - 90 x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $h (x)$ $=$ $3 x^{4} + 12 x^{3} - 33 x^{2} - 90 x$
  ↓
  $3 x$ ausklammern.
  $h (x)$ $=$ $3 x \cdot (x^{3} + 4 x^{2} - 11 x - 30)$
  $\Rightarrow x_{1} = 0$
  Die Funktion $h (x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_{1} = 0$ bereits bekannt ist, kannst du die weiteren Nullstellen von $h$ bestimmen, indem du die Klammer gleich $0$ setzt.
  $x^{3} + 4 x^{2} - 11 x - 30 = 0$
  Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $- 2$ für $x$ ein.
  $(- 2)^{3} + 4 \cdot (- 2)^{2} - 11 \cdot (- 2) - 30 = - 8 + 16 + 22 - 30 = 0$
  Die Funktion $h (x)$ hat an der Stelle $x_{2} = - 2$ eine Nullstelle. Da $h (- 2) = 0$ , wissen wir, dass $h (x)$ den dazugehörigen Linearfaktor $(x + 2)$ besitzt.
  Führe nun die Polynomdivision $(x^{3} + 4 x^{2} - 11 x - 30) : (x + 2)$ durch.
  $\begin{array}{l} (x^{3} + 4 x^{2} - 11 x - 30) : (x + 2) = x^{2} + 2 x - 15 \\ - (x^{3} + 2 x^{2}) \\ 2 x^{2} - 11 x \\ - (2 x^{2} + 4 x) \\ - 15 x - 30 \\ - (- 15 x - 30) \\ 0 \end{array}$
  Setze das erhaltene Polynom gleich $0$ .
  $x^{2} + 2 x - 15$ $=$ $0$
  ↓
  Mitternachtsformel anwenden.
  $x_{3,4}$ $=$ $\frac{- 2 \pm \sqrt{2^{2} - 4 \cdot 1 \cdot (- 15)}}{2 \cdot 1}$
  ↓
  Unter der Wurzel zusammenfassen.
  $x_{3,4}$ $=$ $\frac{- 2 \pm \sqrt{64}}{2}$
  $x_{3,4}$ $=$ $\frac{- 2 \pm 8}{2}$
  Fall 1: $+$
  $x_{3} = \frac{6}{2} = 3$
  Fall 2: $-$
  $x_{4} = \frac{- 10}{2} = - 5$
  Die Funktion $h (x)$ hat vier Nullstellen bei $x_{1} = 0$ , $x_{2} = - 2$ , $x_{3} = 3$ und $x_{4} = - 5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $i (x) = x^{3} - 7 x - 6$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $i (x)$ $=$ $x^{3} - 7 x - 6$
  ↓
  Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. $1$ in $i (x)$ ein.
  $i (1)$ $=$ $1^{3} - 7 \cdot 1 - 6$
  $i (1)$ $=$ $- 12$
  $i (1) \neq 0$
  Setze z.B. $- 1$ in $i (x)$ ein.
  $i (- 1) = (- 1)^{3} - 7 \cdot (- 1) - 6 = 0$
  Die Funktion $i (x)$ hat an der Stelle $x_{1} = - 1$ eine Nullstelle. Da $i (- 1) = 0$ , wissen wir, dass $i (x)$ den dazugehörigen Linearfaktor $(x + 1)$ besitzt.
  Führe nun die Polynomdivision $i (x) : (x + 1)$ durch.
  $\begin{matrix} - (x^{3} + 0 x^{2} - 7 x - 6) : (x + 1) = x^{2} - x - 6 \\ - (x^{3} + x^{2}) \\ - x^{2} - 7 x \\ - (- x^{2} - x) \\ - 6 x - 6 \\ - (- 6 x - 6) \\ 0 \end{matrix}$
  Die Funktion $i (x)$ wird dann $0$ , sobald mindestens einer der Faktoren gleich $0$ ist. Da die Nullstelle $x_{1} = - 1$ bereits bekannt ist, kannst du die weiteren Nullstellen von $i$ bestimmen, indem du das erhaltene Polynom gleich $0$ setzt.
  $x^{2} - x - 6$ $=$ $0$
  ↓
  Mitternachtsformel anwenden.
  $x_{2,3}$ $=$ $\frac{1 \pm \sqrt{{(- 1)}^{2} - 4 \cdot 1 \cdot (- 6)}}{2 \cdot 1}$
  ↓
  Unter der Wurzel zusammenfassen.
  $x_{2,3}$ $=$ $\frac{1 \pm \sqrt{25}}{2}$
  $x_{2,3}$ $=$ $\frac{1 \pm 5}{2}$
  $x_{2} = \frac{6}{2} = 3$
  $x_{3} = \frac{- 4}{2} = - 2$
  Fall 1: $+$
  Fall 2: $-$
  Die Funktion $i (x)$ hat drei Nullstellen bei $x_{1} = - 1$ , $x_{2} = 3$ und $x_{3} = - 2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
17
Gegeben ist die Funktionenschar $f_{a} (x) = a x^{2} + 6 x - 3$ mit $a \neq 0$ .
1. Ermittle die Nullstellen der Funktion in Abhängigkeit des Parameters $a$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f_{a} (x)$ $=$ $a x^{2} + 6 x - 3$
  ↓
  Setze die Funktion gleich 0.
  $a x^{2} + 6 x - 3$ $=$ $0$
  ↓
  Mitternachtsformel anwenden.
  $x_{1,2}$ $=$ $\frac{- 6 \pm \sqrt{6^{2} - 4 \cdot a \cdot (- 3)}}{2 \cdot a}$
  ↓
  Unter der Wurzel zusammenfassen.
  $x_{1,2}$ $=$ $\frac{- 6 \pm \sqrt{36 + 12 a}}{2 a}$
  Dieser Term kann auch noch weiter gekürzt werden. Für die Bearbeitung dieser Aufgabe ist das jedoch nicht notwendig. Im Folgenden wird der Term noch weiter vereinfacht:
  Unter der Wurzel kannst du die $4$ ausklammern.
  $x_{1,2}$ $=$ $\frac{- 6 \pm \sqrt{4 \cdot (9 + 3 a)}}{2 a}$
  ↓
  4 aus der Wurzel kürzen.
  $x_{1,2}$ $=$ $\frac{- 6 \pm 2 \sqrt{9 + 3 a}}{2 a}$
  ↓
  2 ausklammern.
  $x_{1,2}$ $=$ $\frac{2 \cdot (- 3 \pm \sqrt{9 + 3 a})}{2 a}$
  ↓
  Bruch kürzen.
  $x_{1,2}$ $=$ $\frac{- 3 \pm \sqrt{9 + 3 a}}{a}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme $a$ so, dass es genau eine Nullstelle gibt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  Aus Aufgabe $a)$ weißt du, dass die Nullstellen bei $x_{1,2} = \frac{- 3 \pm \sqrt{9 + 3 a}}{a}$ liegen.
  Die Funktion hat genau eine Nullstelle, wenn die Diskriminante gleich Null wird.
  $D$ $=$ $9 + 3 a$
  ↓
  Setze die Diskriminante gleich Null.
  $0$ $=$ $9 + 3 a$ $- 9$
  $- 9$ $=$ $3 a$ $: 3$
  $a$ $=$ $- 3$
  DIe Funktion $f_{a} (x)$ hat für $a = - 3$ genau eine Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Bestimme $a$ so, dass $x = - 1$ eine Nullstelle ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  Aus Aufgabe $a)$ weißt du, dass die Nullstellen bei $x_{1,2} = \frac{- 3 \pm \sqrt{9 + 3 a}}{a}$ liegen.
  Setze den Term gleich $- 1$ und löse die Gleichung.
  $\frac{- 3 \pm \sqrt{9 + 3 a}}{a}$ $=$ $- 1$ $\cdot a$
  $- 3 \pm \sqrt{9 + 3 a}$ $=$ $- a$ $+ 3$
  $\pm \sqrt{9 + 3 a}$ $=$ $- a + 3$ ${()}^{2}$
  $9 + 3 a$ $=$ $a^{2} - 6 a + 9$ $- (9 + 3 a)$
  $0$ $=$ $a^{2} - 9 a$ $: a (möglich, da a \neq 0)$
  $0$ $=$ $a - 9$ $+ 9$
  $9$ $=$ $a$
  Die Funktion $f_{a} (x)$ hat für $a = 9$ eine Nullstelle bei $x = - 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
18
Gegeben ist die Funktionenschar $f_{b} (x) = x^{4} + b x^{2} + 6$ mit $b \neq 0$ .
1. Bestimme die Nullstellen der Funktion in Abhängigkeit von $b$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f_{b} (x)$ $=$ $x^{4} + b x^{2} + 6$
  ↓
  Setze die Funktion gleich $0$ .
  $0$ $=$ $x^{4} - b x^{2} + 6$
  Substitution
  Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. $u$ ) ersetzt. Hier wird $x^{2}$ durch $u$ ersetzt.
  $u^{2} + b u + 6$ $=$ $0$
  ↓
  Mitternachtsformel anwenden.
  $u_{1,2}$ $=$ $\frac{- b \pm \sqrt{b^{2} - 4 \cdot 1 \cdot 6}}{2 \cdot 1}$
  ↓
  Unter der Wurzel zusammenfassen.
  $=$ $\frac{- b \pm \sqrt{b^{2} - 24}}{2}$
  Resubstitution
  Die Resubstitution beschreibt das Rückgängigmachen der Substitution.
  $(x_{1,2,3,4})^{2} = u_{1,2} = \frac{- b \pm \sqrt{b^{2} - 24}}{2}$
  Wurzel ziehen.
  $x_{1,2,3,4} = \pm \sqrt{\frac{- b \pm \sqrt{b^{2} - 24}}{2}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme $b$ so, dass $x = \sqrt{2}$ eine Nullstelle ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  Aus Aufgabe $a)$ weißt du, dass die Nullstellen bei $x_{1,2,3,4} = \pm \sqrt{\frac{- b \pm \sqrt{b^{2} - 24}}{2}}$ liegen.
  Setze den Term gleich $\sqrt{2}$ und löse die Gleichung.
  $\begin{array}{rcl} \pm \sqrt{\frac{- b \pm \sqrt{b^{2} - 24}}{2}} & = & \sqrt{2} & | ()^{2} \\ \frac{- b \pm \sqrt{b^{2} - 24}}{2} & = & 2 & | \cdot 2 \\ - b \pm \sqrt{b^{2} - 24} & = & 4 & | + b \\ \pm \sqrt{b^{2} - 24} & = & b + 4 & | ()^{2} \\ b^{2} - 24 & = & b^{2} + 8 b + 16 & | - (b^{2} + 16) \\ - 40 & = & 8 b & | : 8 \\ - 5 & = & b \end{array}$
  Die Funktion $f_{b} (x)$ hat für $b = - 5$ eine Nullstelle bei $x = \sqrt{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
19
Gegeben ist die Funktionenschar $f_{k} (x) = k x^{2} + k x - 7,5$ mit $k \neq 0$ .
1. Bestimme $k$ so, dass es nur eine Nullstelle gibt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f_{k} (x) = k x^{2} + k x - 7,5$
  Die Funktion hat genau eine Nullstelle, wenn die Diskriminante gleich Null wird.
  $D$ $=$ $k^{2} - 4 \cdot k \cdot (- 7,5)$
  ↓
  Setze die Diskriminante gleich Null.
  $=$ $k^{2} + 30 k$
  $k^{2} + 30 k$ $=$ $0$ $k$
  ↓
  Da $k \neq 0$ kannst du durch $k$ teilen
  $k + 30$ $=$ $0$ $- 30$
  $k$ $=$ $- 30$
  DIe Funktion $f_{k} (x)$ hat für $k = - 30$ genau eine Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme $k$ so, dass $x = - 2,5$ eine Nullstelle ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenbestimmung
  Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.
  $f_{k} (x)$ $=$ $k x^{2} + k x - 7,5$
  ↓
  Setze die Funktion gleich $0$ .
  $k x^{2} + k x - 7,5$ $=$ $0$
  ↓
  Mitternachtsformel anwenden.
  $x_{1,2}$ $=$ $\frac{- k \pm \sqrt{k^{2} 4 \cdot k \cdot (- 7,5)}}{2 \cdot k}$
  ↓
  Unter der Wurzel zusammenfassen.
  $=$ $\frac{- k \pm \sqrt{k^{2} + 30 k}}{2 k}$
  Setze den Term gleich $- 2,5$ und löse die Gleichung.
  $\begin{array}{rcl} \frac{- k \pm \sqrt{k^{2} + 30 k}}{2 k} & = & - 2,5 & | \cdot 2 k \\ - k \pm \sqrt{k^{2} + 30 k} & = & - 5 k & | + k \\ \pm \sqrt{k^{2} + 30 k} & = & - 4 k & | ()^{2} \\ k^{2} + 30 k & = & 16 k^{2} & | - (k^{2} + 30 k) \\ 0 & = & 15 k^{2} - 30 k & | : k (möglich, da k \neq 0) \\ 0 & = & 15 k - 30 & | + 30 \\ 30 & = & 15 k & | : 15 \\ 2 & = & k \end{array}$
  Die Funktion $f_{k} (x)$ für $k = 2$ eine Nullstelle bei $x = - 2,5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$f (x)$	$=$	$2 x - 8$
	↓	Setze $f (x) = 0$
$2 x - 8$	$=$	$0$	$+ 8$
$2 x$	$=$	$8$	$: 2$
$x$	$=$	$4$

$g (x)$	$=$	$- x^{2} - 7 x - 10$
	↓	Setze $g (x) = 0$
$- x^{2} - 7 x - 10$	$=$	$0$
	↓	Wende die Mitternachtsformel an.
$x_{1,2}$	$=$	$\frac{- (- 7) \pm \sqrt{(- 7)^{2} - 4 (- 1) (- 10)}}{2 (- 1)}$
	↓	Multipliziere die Klammern aus.
$x_{1,2}$	$=$	$\frac{7 \pm \sqrt{49 - 40}}{- 2}$
	↓	Berechne die Wurzel
$x_{1,2}$	$=$	$\frac{7 \pm 3}{- 2}$
	↓	1 Fall: $+$
$x_{1}$	$=$	$\frac{10}{- 2}$
	$=$	$- 5$
	↓	2 Fall: $-$
$x_{2}$	$=$	$\frac{7 - 3}{- 2}$
	$=$	$- 2$

$f (x)$	$=$	$4 x + 20$
	↓	Setze f(x)=0
$4 x + 20$	$=$	$0$	$- 20$
$4 x$	$=$	$- 20$	$: 4$
$x$	$=$	$- 5$

$f (x)$	$=$	$14 x - 21$
	↓	Setze f(x)=0
$14 x - 21$	$=$	$0$	$+ 21$
$14 x$	$=$	$21$	$: 14$
$x$	$=$	$1,5$

$f (x)$	$=$	$x^{2} + 6 x - 14 = 0$
	↓	mit der pq-Formel lösen.
$x_{1,2}$	$=$	$- (\frac{p}{2}) \pm \sqrt{{(\frac{p}{2})}^{2} - q}$

$x_{1,2}$	$=$	$- 3 \pm \sqrt{9 - (- 14)}$
$x_{1}$	$=$	$- 3 + \sqrt{23} \lor x_{2} = - 3 - \sqrt{23}$

$f (x)$	$=$	$x^{2} - 5 x + 6 = 0$
	↓	Bestimme die Koeffizienten a, b und c.
$a$	$=$	$1$
$b$	$=$	$- 5$
$c$	$=$	$6$
	↓	Setze nun die 3 Koeffizienten in die Mitternachtsformel ein.
$x_{1,2}$	$=$	$\frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 \cdot 1 \cdot 6}}{2 \cdot 1}$
	$=$	$\frac{5 \pm \sqrt{25 - 24}}{2}$
	$=$	$\frac{5 \pm 1}{2}$
$x_{1}$	$=$	$3$
$x_{2}$	$=$	$2$

$x^{2} - 5 x + 6$	$=$	$0$
	↓	Da die Gleichung die Form $x^{2} + p x + q = 0$ hat, können wir den Satz von Vieta anwenden.
$x_{1} + x_{2}$	$=$	$- p = - (- 5) = 5$
$x_{1} \cdot x_{2}$	$=$	$q = 6$

$f (x)$	$=$	$x^{4} - 3 x^{2} + 2$
	↓	f(x) gleich 0 setzen, um die Nullstellen zu bestimmen
$x^{4} - 3 x^{2} + 2$	$=$	$0$

$u$	$=$	$x^{2}$
$f (u)$	$=$	$u^{2} - 3 u + 2 = 0$
	↓	Mitternachtsformel anwenden
$u_{1,2}$	$=$	$\frac{3 \pm \sqrt{{(- 3)}^{2} - 4 \cdot 1 \cdot 2}}{2 \cdot 1}$
	↓	Unter der Wurzel ausmultiplizieren.
	$=$	$\frac{3 \pm \sqrt{9 - 8}}{2}$
	↓	Wurzel ziehen.
	$=$	$\frac{3 \pm 1}{2}$

$x_{3,4}^{2}$	$=$	$\frac{1}{4}$
	↓	Wurzel ziehen
$x_{3,4}$	$=$	$\pm \frac{1}{2}$

$x_{1,2}^{2}$	$=$	$\frac{3}{2}$
	↓	Wuzel ziehen
$x_{1}$	$=$	$\sqrt{\frac{3}{2}}$
$x_{2}$	$=$	$- \sqrt{\frac{3}{2}}$
	↓	Zwei doppelte Nullstellen

$u_{1}$	$=$	$2 + \sqrt{8} \approx 4,83$
	↓	Fall: +

$u_{2}$	$=$	$2 - \sqrt{8} \approx - 0,83$
	↓	Fall: -

$u$	$=$	$x^{2}$
$f (u)$	$=$	$u^{2} - \frac{17}{4} u + 1$
	↓	Mitternachtsformal anwenden
$u_{1 / 2}$	$=$	$\frac{\frac{17}{4} \pm \sqrt{(- \frac{17}{4})^{2} - 4 \cdot 1 \cdot 1}}{2}$
	↓	Unter der Wurzel ausmultiplizieren
	$=$	$\frac{\frac{17}{4} \pm \sqrt{14,0625}}{2}$
	↓	Wurzel ziehen
	$=$	$\frac{\frac{17}{4} \pm \frac{15}{4}}{2}$

$u$	$=$	$x^{2}$
$f (u)$	$=$	$(u - \frac{3}{2})^{2} = (u - \frac{3}{2}) (u - \frac{3}{2})$
	↓	Die Nullstellen können abgelesen werden
$u$	$=$	$\frac{3}{2}$
	↓	Doppelte Nullstelle

$u$	$=$	$x^{3}$
$f (u)$	$=$	$\frac{1}{2} u^{2} - 2 u - 2$
	↓	Mitternachtsformel anwenden
$u_{1,2}$	$=$	$\frac{2 \pm \sqrt{(- 2)^{2} - 4 \cdot \frac{1}{2} \cdot (- 2)}}{2 \cdot \frac{1}{2}}$
	$=$	$\frac{2 \pm \sqrt{8}}{1} = 2 \pm \sqrt{8}$

$x_{1}^{3}$	$\approx$	$4,83$
	↓	dritte Wurzel ziehen
$x_{1}$	$\approx$	$\sqrt[3]{4,83} \approx 1,69$

$x_{2}^{3}$	$\approx$	$- 0,83$
	↓	dritte Wurzel ziehen
$x_{2}$	$\approx$	$\sqrt[3]{- 0,83} \approx - 0,94$

$f (x)$	$=$	$x^{3} + 3 x^{2} - 4 x$
	↓	Setze die Funktion gleich 0.
$0$	$=$	$x^{3} + 3 x^{2} - 4 x$
	↓	Klammere $x$ aus.
$0$	$=$	$x (x^{2} + 3 x - 4)$

$x_{2,3}$	$=$	$\frac{- 3 \pm \sqrt{3^{2} - 4 \cdot 1 \cdot (- 4)}}{2 \cdot 1}$
	↓	Fasse unter der Wurzel zusammen.
	$=$	$\frac{- 3 \pm \sqrt{9 + 16}}{2}$
	$=$	$\frac{- 3 \pm \sqrt{25}}{2}$
	↓	Ziehe die Wurzel
	$=$	$\frac{- 3 \pm 5}{2}$

$f (x)$	$=$	$x^{4} + 2 x^{3} + x^{2}$
	↓	Klammere die kleinste Potenz von $x$ aus und setze $f (x)$ = 0
$0$	$=$	$x^{2} \cdot (x^{2} + 2 x + 1)$

$0$	$=$	$(x^{2} - 25)$
	↓	Benutze die 3. Binomische Formel
$0$	$=$	$(x - 5) \cdot (x + 5)$

$0$	$=$	$\frac{1}{2} x + 4$	$- 4$
$- 4$	$=$	$\frac{1}{2} x$	$\cdot 2$
$- 8$	$=$	$x$

Aufgaben zur Nullstelle

Graphische Veranschaulichung:

Lösung durch Berechnung:

Hast du eine Frage oder Feedback?

Graphische Veranschaulichung:

Lösung durch Berechnung:

Hast du eine Frage oder Feedback?

Graphische Veranschaulichunng

Lösung durch Berechnung:

Hast du eine Frage oder Feedback?

Graphische Veranschaulichung

Lösung durch Berechnung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Eine mögliche Lösung:

Hast du eine Frage oder Feedback?

Eine mögliche Lösung

Hast du eine Frage oder Feedback?

Roter Graph

Grüner Graph

Lila Graph

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Resubstitution

Hast du eine Frage oder Feedback?

Ersetze den "schlimmen Teil"

Nullstellen des linken Faktors

Nullstellen des rechten Faktors

Und die Nullstellen von f lauten…

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nun zur Substitution:

Zum Schluss muss natürlich die Resubstitution angewandt:

Hast du eine Frage oder Feedback?

Nun zur Substitution:

Resubstitution

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Substitution

Resubstitution

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Substitution

Nullstellenbestimmung

Und die Nullstellen von $f$ lauten…

Anwenden der 1. binomischen Formel für $x_{3,4}$

$f (x)$	$=$	$x^{2} - 6 x + 9$
	↓	Setze die Funktion gleich 0.
$0$	$=$	$x^{2} - 6 x + 9$
	↓	Wende die 2. Binomische Formel an.
$0$	$=$	${(x - 3)}^{2}$
$0$	$=$	$(x - 3) \cdot (x - 3)$

$f (x)$	$=$	$x^{6} - x^{4}$
	↓	Setze die Funktion gleich 0.
$0$	$=$	$x^{6} - x^{4}$
	↓	Klammere die kleinste Potenz von $x$ aus.
$0$	$=$	$x^{4} \cdot (x^{2} - 1)$

$0$	$=$	$(x^{2} - 1)$
	↓	Verwende die 3. Binomische Formel.
$0$	$=$	$(x - 1) \cdot (x + 1)$

$f (x)$	$=$	$u^{2} - 6 u + 5$
	↓	Setze die Funktion gleich 0.
$0$	$=$	$u^{2} - 6 u + 5$

$u_{1,2}$	$=$	$\frac{6 \pm \sqrt{(- 6)^{2} - 4 \cdot 1 \cdot 5}}{2 \cdot 1}$
	↓	Fasse unter der Wurzel zusammen.
	$=$	$\frac{6 \pm \sqrt{36 - 20}}{2}$
	$=$	$\frac{6 \pm \sqrt{16}}{2}$
	$=$	$\frac{6 \pm 4}{2}$

$x_{2,3}$	$=$	$\frac{- 1 \pm \sqrt{1^{2} - 4 \cdot 1 \cdot (- 6)}}{2 \cdot 1}$
	↓	Fasse unter der Wurzel zusammen
	$=$	$\frac{- 1 \pm \sqrt{25}}{2 \cdot 1}$
	$=$	$\frac{- 1 \pm 5}{2 \cdot 1}$

$f (x)$	$=$	$\frac{1}{4} x^{5} - 3 x^{3} + 8 x$
	↓	Setze die Funktion gleich 0.
$0$	$=$	$\frac{1}{4} x^{5} - 3 x^{3} + 8 x$
	↓	$ x$ ausklammern.
	$=$	$x \cdot (\frac{1}{4} x^{4} - 3 x^{2} + 8)$
$x_{1}$	$=$	$0$
$(\frac{1}{4} x^{4} - 3 x^{2} + 8)$	$=$	$0$
	↓	Klammer 0 setzen.

$\frac{1}{4} x^{4} - 3 x^{2} + 8$	$=$	$0$
	↓	$x 2$ wird durch uuu ersetzt.
$\frac{1}{4} u^{2} - 3 u + 8$	$=$	$0$
	↓	Mitternachtsformel anwenden.
$u_{1,2}$	$=$	$\frac{3 \pm \sqrt{{(- 3)}^{2} - 4 \cdot \frac{1}{4} \cdot 8}}{2 \cdot \frac{1}{4}}$
	↓	Unter der Wurzel zusammenfassen.
	$=$	$\frac{3 \pm \sqrt{9 - 8}}{0,5}$
	↓	Unter der Wurzel subtrahieren.
	$=$	$\frac{3 \pm \sqrt{1}}{0,5}$
	↓	Wurzel ziehen.

$x_{2,3}^{2}$	$=$	$u_{1}$
$u_{1}$	$=$	$8$
	↓	Radizieren.
$x_{2,3}$	$=$	$\pm \sqrt{8}$
	$=$	$\pm 2 \sqrt{2}$
$x_{4,5}^{2}$	$=$	$u_{2}$
$u_{2}$	$=$	$4$
	↓	Radizieren.
$x_{4,5}$	$=$	$\pm \sqrt{4}$
	$=$	$\pm 2$

$g (x)$	$=$	$x^{7} - 7 x^{4} - 8 x$
	↓	Setze die Funktion gleich 0.
$0$	$=$	$x^{7} - 7 x^{4} - 8 x$
	↓	$ x$ ausklammern.
	$=$	$x \cdot (x^{6} - 7 x^{3} - 8)$
$x_{1}$	$=$	$0$
$(x^{6} - 7 x^{3} - 8)$	$=$	$0$
	↓	Klammer 0 setzen.