Aufgaben zu linearen Funktionen

1
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Stelle die Gleichung der Geraden durch die Punkte $P (1 | 3)$ und $Q (3 | - 1)$ auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Gegeben sind die beiden Punkte $P (1 | 3)$ und $Q (3 | - 1)$ .
Gesucht ist die Gleichung der Geraden, die durch die beiden Punkte geht.
Zur Ermittlung der Geradengleichung überlegst du am Besten erst die allgemeine Form der Geradengleichung:
Bestimmung der Steigung $m$
Erinnere dich zunächst an die Gleichung für die Steigung einer Geraden:
$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
Setze die Werte $x_{1}, x_{2}, y_{1}, y_{2}$ aus den Punkten $P$ und $Q$ in die Formel ein.
$m = \frac{- 1 - 3}{3 - 1} = \frac{- 4}{2}$
Kürze den Bruch.
$m = - 2$
Jetzt weißt du, dass die Gleichung der Geraden durch die Punkte $P$ und $Q$ geht folgendermaßen aussieht:
$y = - 2 \cdot x + t .$
Als nächstes ermittelst du den $y$ -Achsenabschnitt ( $t$ ).
Ermittlung des $y$ -Achsenabschnitts $t$
Um $t$ zu ermitteln setzt du den $x$ - und $y$ -Wert einer der beiden Punkte in die Geradengleichung ein. Hier wird das beispielhaft mit dem Punkt $P$ ausgerechnet.
$3 = - 2 \cdot 1 + t$
$3 = - 2 + t$
$t = 5$
Der $y$ -Achsenabschnitt der Funktion ist $5$ . Damit hast du auch schon die ganze Funktionsgleichung.
$y = - 2 \cdot x + 5$
2
Berechne die Steigung der Gerade durch die gegebenen Punkte.
1. $A (5 | 7)$ , $B (- 3 | 8)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
  $A (5 | 7), B (- 3 | 8)$
  Setze die Punkte in den Differenzenquotient für die Gerade ein.
  $m$ $=$ $\frac{8 - 7}{- 3 - 5}$
  ↓
  Vereinfache Zähler und Nenner
  $m$ $=$ $\frac{1}{- 8}$
  $m$ $=$ $- \frac{1}{8}$
  Die Steigung der Geraden beträgt $m = - \frac{1}{8}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $A (1 | 2)$ , $B (3 | 4)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
  $A (1 | 2), B (3 | 4)$
  Setze die Punkte in den Differenzenquotient für die Gerade ein.
  $m$ $=$ $\frac{4 - 2}{3 - 1}$
  ↓
  Vereinfache Zähler und Nenner
  $m$ $=$ $\frac{2}{2}$
  $m$ $=$ $1$
  Die Steigung der Geraden beträgt m = 1.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
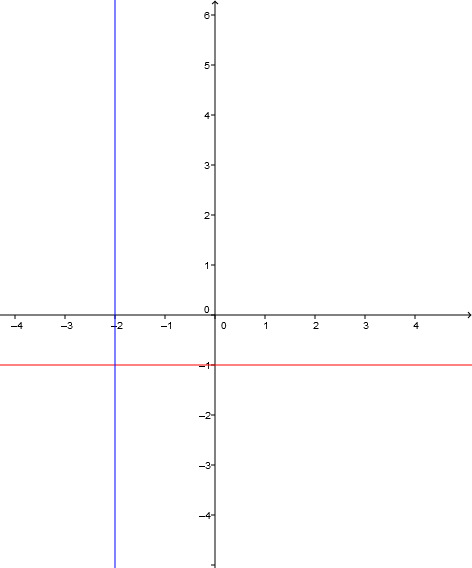
Berechnen Sie den Abstand der parallelen Geraden g: $y = - \frac{1}{2} x + 2$ und h: $y = - \frac{1}{2} x - 3$ .
Rundet das Ergebnis auf zwei Stellen nach dem Komma.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Geraden
Abstand zweier paralleler Geraden
Der kürzeste Weg zwischen zwei parallelen Geraden ist eine Normale der Geraden .
Der Abstand der Geraden entspricht dem Abstand zwischen den beiden Schnittpunkten der Normale mit den Geraden .
Skizze
Fertige eine Skizze an.
Geradengleichung
Stelle die Geradengleichung der Normalen d auf.
Berechne dazu zunächst die Steigung.
$m_{d} \cdot m_{g}$ $=$ $- 1$ $: m_{g}$
$m_{d}$ $=$ $\frac{- 1}{m_{g}}$
↓
Setze die Steigung der Funktion $m_{g}$ (nämlich $- \frac{1}{2}$ ) ein.
$m_{d}$ $=$ $\frac{- 1}{- \frac{1}{2}}$
↓
Vereinfache die rechte Seite.
$m_{d}$ $=$ $- 2$
Stelle nun die Geradengleichung auf.
Es wird ein Punkt T, der auf der Geraden liegt benötigt. Verwendet wird der y-Abschnitt von $h (x)$ : $(0 | - 3)$ .
Setze $T (0 | - 3)$ (siehe Skizze) und $m_{d}$ in die allgemeine Geradengleichung ein um t zu bestimmen.
$- 3$ $=$ $2 \cdot (0) + t$
↓
Multipliziere aus .
$t$ $=$ $- 3$
↓
Setze t und $m_{d}$ in die allgemeine Geradengleichung ein.
$y$ $=$ $2 x - 3$
Bestimme den Schnittpunkt von d und g
Berechne zunächst die x-Koordinate des Schnittpunkts S.
Normale d: $y = 2 x - 3$
Gerade g: $y = - \frac{1}{2} x + 2$
Setze die Funktionen gleich.
$2 x - 3$ $=$ $- \frac{1}{2} x + 2$ $+ 3$
$2 x$ $=$ $- \frac{1}{2} x + 5$ $+ \frac{1}{2} x$
$\frac{5}{2} x$ $=$ $5$ $: \frac{5}{2}$
$x$ $=$ $2$
Berechne nun die y-Koordinate des Schnittpunkts S.
$y$ $=$ $2 x - 3$
↓
Setze das gefundene x = 2 ein.
$y$ $=$ $2 \cdot 2 - 3$
↓
Rechne aus.
$y$ $=$ $1$
Gib die Koordinaten des Schnittpunktes S an.
$\Rightarrow$ $S (2 | 1)$
Bestimme den Abstand der Punkte S und T.
Bestimme den Abstand in x-Richtung.
$T (0 | - 3)$ , $S (2 | 1)$
Berechne die Differenz der x-Werte von S und T.
$Δ x = 2 - 0 = 2$
Bestimme den Abstand in y-Richtung.
$T (0 | - 3)$ , $S (2 | 1)$
Berechne die Differenz der y-Werte.
$Δ y = 1 - (- 3) = 4$
Bestimme den Abstand in direkter Linie zwischen den Punkten.
$Δ x = 2$
$Δ y = 4$
Wende den Satz des Pythagoras an.
$d^{2}$ $=$ $2^{2} + 4^{2}$
↓
Berechne die beiden Potenzen.
$d^{2}$ $=$ $4 + 16$
↓
Addiere.
$d^{2}$ $=$ $20$
↓
Ziehe die Wurzel.
$d$ $=$ $\sqrt{20}$
Wenn du $\sqrt{20}$ in den Taschenrechner eingibst und das Ergebnis auf zwei Stellen nach dem Komma rundest, erhältst du:
$d = \sqrt{20} \approx 4,47$
Ergebnis
Der Abstand der beiden Geraden beträgt etwa 4,47.
4
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Eine Zeitschrift, die zum Preis von $2,20$  € zu kaufen ist, hat eine Auflage von $120 000$ Exemplaren. Mit Hilfe der Marktforschung stellt der Verlag fest, dass sich die Auflage bei einer Preissenkung um $0,20$  € pro Zeitschrift um $5000$ Exemplare erhöhen lässt, bei einer Preiserhöhung von $0,20$  € verliert man $5000$ Käufer.
1. Berechnen Sie den Preis bei einer Auflage von 140 000 Exemplaren.
  €
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Wachstum
  Anstieg auf 140 000 Exemplare
  Bestimme, um wieviel sich die Auflage verändert hat.
  $Δ N = 140 000 - 120 000 = 20 000$
  Bestimme die Änderungsrate a aus der Aufgabenstellung. Beachte, dass dabei die bekannte Änderung (N) im Nenner steht.
  $a = \frac{Δ p}{Δ N} = \frac{- 0,2}{5000} = - 0,00004$
  Bestimme daraus die Preisänderung.
  $Δ p = a \cdot Δ N = - 0,00004 \cdot 20 000 = - 0,8$
  Berechne damit den neuen Preis.
  $p_{n e u} = p_{a l t} + Δ p = 2,2 - 0,8 = 1,4$
  Bei einer Auflage von 140 000 beträgt der Preis also 1,40€.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Welche Verkaufszahlen kann der Verlag erwarten, wenn er den Preis der Zeitschrift auf 1,50€ senkt?
  Stück
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Wachstum
  Der Preis ist auf 1,50€ gefallen.
  Bestimme die Preisänderung.
  $Δ p = p_{n e u} - p_{a l t} = 1,5 - 2,2 = - 0,7$
  Bestimme Änderungsrate a aus der Aufgabenstellung. Beachte dabei, dass die bekannte Änderung (p) im Nenner steht.
  $a = \frac{Δ N}{Δ p} = \frac{- 5000}{0,2} = - 25 000$
  Bestimme damit die Änderung der Auflage.
  $Δ N = a \cdot Δ p = (- 25 000) \cdot (- 0,7) = 17 500$
  Bestimme die neue Auflage.
  $N_{n e u} = N_{a l t} + Δ N = 120 000 + 17 500 = 137 500$
  Bei einem Preis von 1,50€ ist die Auflage also 137 500 Stück.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
Berechne den Abstand der Geraden zum Ursprung.
1. $y = \frac{3}{4} x - 5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Senkrechten
  Geradensteigung und Geradengleichung
  Der kürzeste Abstand zum Ursprung ist die Senkrechte auf die Gerade durch den Ursprung. Ist $g (x) : y = m_{1} \cdot x + b$ , so berechnest du die Steigung der Senkrechten $m_{2}$ mit der Formel.
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert der Steigung ein.
  $m_{2} = - \frac{1}{\frac{3}{4}} = - \frac{4}{3}$
  Die gesuchte Senkrechte hat also Steigung $- \frac{4}{3}$ und geht durch den Ursprung, der y-Achsenabschnitt $b$ ist also 0. Damit lautet die Geradengleichung der Senkrechte $h (x) : y = - \frac{4}{3} x$ .
  Berechne nun den Schnittpunkt $A (x_{s} | y_{s})$ der beiden Geraden indem du ihre Geradengleichungen gleichsetzt.
  $g (x_{s})$ $=$ $h (x_{s})$
  ↓
  Setz die Geradengleichungen ein.
  $- \frac{4}{3} x_{s}$ $=$ $\frac{3}{4} x_{s} - 5$ $- \frac{3}{4} x_{s}$
  ↓
  Bringe die Variable $x_{s}$ auf die linke Seite.
  $- \frac{25}{12} x_{s}$ $=$ $- 5$ $\cdot (- 1)$
  $\frac{25}{12} x_{s}$ $=$ $5$ $: \frac{25}{12}$
  $x_{s}$ $=$ $\frac{12}{5}$
  $=$ $2,4$
  Setz nun $x_{s}$ in eine der Geradengleichungen ein um $y_{s}$ zu bestimmen.
  $h (x_{s}) : y_{s} = - \frac{4}{3} x_{s}$
  Setz $x_{s} = 2,4$ ein.
  $y_{s} = - \frac{4}{3} \cdot 2,4 = - 3,2$
  Der Schnittpunkt der Geraden $h$ und $g$ liegt also bei $A (2,4 | - 3,2)$ .
  Bestimme nun den Abstand des Ursprungs zum berechneten Schnittpunkt $A$ , dies ist genau der kürzeste Abstand der Geraden $g$ zum Ursprung.
  $d = \sqrt{(x_{s} - x_{0})^{2} + (y_{s} - y_{0})^{2}}$
  Setz die Werte ein.
  $d = \sqrt{(2,4 - 0)^{2} + (- 3,2 - 0)^{2}}$
  Vereinfache.
  $= \sqrt{5,76 + 10,24} = \sqrt{16} = 4$
  Der kürzeste Abstand der Geraden $g$ zum Ursprung ist also 4.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $y = - \frac{1}{2} x + 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
  Der kürzeste Abstand zum Ursprung ist die Senkrechte auf die Gerade durch den Ursprung. Ist $g (x) : y = m_{1} \cdot x + b$ , so berechnest du die Steigung der Senkrechten $m_{2}$ mit der Formel
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert der Steigung ein.
  $m_{2} = - \frac{1}{- \frac{1}{2}} = 2$
  Die gesuchte Senkrechte hat also Steigung $2$ und geht durch den Ursprung, der y-Achsenabschnitt $b$ ist also 0. Damit lautet die Geradengleichung der Senkrechte $h (x) : y = 2 x$ .
  Berechne nun den Schnittpunkt $A (x_{s} | y_{s})$ der beiden Geraden, indem du ihre Geradengleichungen gleichsetzt.
  $g (x_{s})$ $=$ $h (x_{s})$
  ↓
  Setz die Geradengleichungen ein.
  $- \frac{1}{2} x_{s} + 2$ $=$ $2 x_{s}$ $- 2 x_{s}$
  ↓
  Bringe die Variable $x_{s}$ auf die linke Seite.
  $- 2,5 x_{s} + 2$ $=$ $0$ $- 2$
  ↓
  Bringe die 2 auf die rechte Seite.
  $- 2,5 x_{s}$ $=$ $- 2$ $: (- 2,5)$
  $x_{s}$ $=$ $0,8$
  Setz nun $x_{s}$ in eine der Geradengleichungen ein um $y_{s}$ zu bestimmen.
  $h (x_{s}) : y_{s} = 2 x_{s}$
  Setz $x_{s} = 0,8$ ein.
  $y_{s} = 2 \cdot 0,8 = 1,6$
  Der Schnittpunkt der Geraden $h$ und $g$ liegt also bei $A (0,8 | 1,6)$ .
  Bestimme nun den Abstand des Ursprungs zum berechneten Schnittpunkt $A$ , dies ist genau der kürzeste Abstand der Geraden $g$ zum Ursprung.
  $d = \sqrt{(x_{s} - x_{0})^{2} + (y_{s} - y_{0})^{2}}$
  Setz die Werte ein.
  $d = \sqrt{(0,8 - 0)^{2} + (1,6 - 0)^{2}}$
  Vereinfache.
  $= \sqrt{0,64 + 2,56} = \sqrt{3,2} \approx 1,79$
  Der kürzeste Abstand der Geraden $g$ zum Ursprung ist also etwa $1,79$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Welche Steigung hat die Gerade durch die Punkte $P (0 | 3)$ und $Q (2 | - 3)$ ? Wie lautet also die Funktionsgleichung?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Steigung
Bestimme die Steigung $m$ .
$m = \frac{△ y}{△ x} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
Setze die beiden Punkte in die Formel für die Steigung ein.
$m = \frac{3 - (- 3)}{0 - 2} = \frac{6}{- 2} = - 3$
Funktionsgleichung
Bestimme die Funktionsgleichung.
$y = m \cdot x + t$
Setze m in die allgemeine Geradengleichung ein.
$y = - 3 x + t$
Setze einen der beiden Punkte in die Funktionsgleichung ein.
$3 = - 3 \cdot 0 + t$
$t = 3$
Setze t in die Funktionsgleichung ein.
$\Rightarrow f (x) = - 3 x + 3$
7
Bestimme den Flächeninhalt des Dreiecks, das von den Koordinatenachsen und der Gerade $g : y = \frac{2}{3} x + 5$ eingeschlossen wird.
Schreibe dein Ergebnis ohne Flächeneinheiten in das Antwortfeld.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Formel zur Berechnung der Dreiecksfläche
Dreiecksfläche
Da die Koordinatenachsen senkrecht aufeinander stehen, können sie als Grundlinie und Höhe der Formel zur Berechnung der Dreiecksfläche benutzt werden.
Höhe ermittlen
g: $y = \frac{2}{3} x + 5$
Der y-Achsenabschnitt ist als t der Geradengleichung gegeben.
Die Gerade schneidet die y-Achse also in (0|5).
Mit der x-Achse als Grundline ergibt sich der Abstand des Punktes zum Ursprung als Höhe.
$\Rightarrow$ Die Höhe h = $\sqrt{5^{2} - 0^{2}} = 5$
Grundlinie berechnen
Für die Angabe der Grundlinie muss der Schnittpunkt der Geraden mit der x-Achse berechnet werden. Setze y dafür 0.
$0 = \frac{2}{3} x + 5$
Nach x auflösen. $| - 5$
$\frac{2}{3} x = - 5$
$| : \frac{2}{3}$
$x = - \frac{15}{2} = - 7,5$
Die Gerade schneidet die x-Achse also in (-7,5|0)
Der Abstand dieses Punktes zum Ursprung ist also die Länge der Grundlinie.
$\Rightarrow$ Die Länge der Grundlinie g ist $\sqrt{(- 7,5)^{2} + 0^{2}} = 7,5$ .
Fläche berechnen
Setze Grundlinie und Höhe in die Formel zur Berechnung der Dreiecksfläche ein.
$\Rightarrow A = \frac{5 \cdot 7,5}{2} = 18,75 FE$
FE steht für "Flächeneinheiten".
Skizze zur Veranschaulichung
8
Bestimme die Gleichung der Geraden, die durch den Punkt P geht und senkrecht zur gegebenen Gerade steht.
1. $y = 3 x + 2$
  $P (3 | 5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g (x) : y = 3 x + 2$ senkrechten Geraden $h$ mit der Formel.
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert ein.
  $m_{2} = - \frac{1}{3}$
  Die gesuchte Senkrechte hat also Steigung $- \frac{1}{3}$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (3 | 5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h (x_{p}) : y_{p} = m_{2} x_{p} + b$
  Setze die Werte ein.
  $5 = - \frac{1}{3} \cdot 3 + b | + 1$
  Vereinfache und addiere $1$ .
  $6 = b \Leftrightarrow b = 6$
  Also lautet die gesuchte Geradengleichung $h (x) : y = - \frac{1}{3} x + 6$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $y = 0,5 x + 1$
  $P (1 | 2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g (x) : y = 0,5 x + 1$ senkrechten Geraden $h$ mit der Formel.
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert ein.
  $m_{2} = - \frac{1}{0,5} = - \frac{1}{\frac{1}{2}} = - 2$
  Die gesuchte Senkrechte hat also Steigung $- 2$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (1 | 2)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h (x_{p}) : y_{p} = m_{2} x_{p} + b$
  Setz die Werte ein.
  $2 = - 2 \cdot 1 + b$ $| + 2$
  Vereinfache und addiere 2.
  $4 = b \Rightarrow b = 4$
  Also lautet die gesuchte Geradengleichung $h (x) : y = - 2 x + 4$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $y = - 5 x + 6$
  $P (- 10 | 1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g (x) : y = - 5 x + 6$ senkrechten Geraden $h$ mit der Formel.
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert ein.
  $m_{2} = - \frac{1}{- 5} = 0,2$
  Die gesuchte Senkrechte hat also Steigung $0,2$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (- 10 | 1)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h (x_{p}) : y_{p} = m_{2} x_{p} + b$
  Setz die Werte ein.
  $1 = 0,2 \cdot (- 10) + b$ $| + 2$
  Vereinfache und addiere 2.
  $3 = b \Rightarrow b = 3$
  Also lautet die gesuchte Geradengleichung $h (x) : y = 0,2 x + 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $y = 4 x + 3$
  $P (2 | - 5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g (x) : y = 4 x + 3$ senkrechten Geraden $h$ mit der Formel.
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert ein.
  $m_{2} = - \frac{1}{4} = - 0,25$
  Die gesuchte Senkrechte hat also Steigung $- 0,25$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (2 | - 5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h (x_{p}) : y_{p} = m_{2} x_{p} + b$
  Setz die Werte ein.
  $- 5 = - 0,25 \cdot 2 + b$ $+ 0,5$
  Vereinfache und addiere 0,5.
  $- 4,5 = b \Rightarrow b = - 4,5$
  Also lautet die Geradengleichung $h (x) : y = - 0,25 x - 4,5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $y = - \frac{2}{3} x + 2$
  $P (4 | 6)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g (x) : y = - \frac{2}{3} x + 3$ senkrechten Geraden $h$ mit der Formel.
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert ein.
  $m_{2} = - \frac{1}{- \frac{2}{3}} = \frac{3}{2}$
  Die gesuchte Senkrechte hat also Steigung $\frac{3}{2}$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (4 | 6)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h (x_{p}) : y_{p} = m_{2} x_{p} + b$
  Setz die Werte ein.
  $6 = \frac{3}{2} \cdot 4 + b$ $| - 6$
  Vereinfache und subtrahiere 6.
  $0 = b \Rightarrow b = 0$
  Also lautet die Geradengleichung $h (x) : y = \frac{3}{2} x$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $y = \frac{1}{3} x - 2$
  $P (2 | 5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g (x) : y = \frac{1}{3} x - 2$ senkrechten Geraden $h$ mit der Formel.
  $m_{2} = - \frac{1}{m_{1}}$
  Setz den Wert ein.
  $m_{2} = - \frac{1}{\frac{1}{3}} = - 3$
  Die gesuchte Senkrechte hat also Steigung $- 3$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (2 | 5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h (x_{p}) : y_{p} = m_{2} x_{p} + b$
  Setz die Werte ein.
  $5 = - 3 \cdot 2 + b$ $| + 6$
  Vereinfache und addiere 6.
  $11 = b \Rightarrow b = 11$
  Also lautet die Geradengleichung $h (x) : y = - 3 x + 11$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
Bestimme die Gleichung der Geraden, die durch …
1. den Punkt $P (- 3 | 4)$ geht und parallel ist zur $x$ -Achse.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur $x$ -Achse, das heißt die gleiche Steigung wie die $x$ -Achse, also $m = 0$ .
  $m$ und $P$ in die allgemeine Geradengeleichung einsetzen.
  $\begin{array}{rcl} 4 & = & 0 \cdot (- 3) + t \\ 4 & = & t \end{array}$
  Zur Geradengleichung zusammensetzen.
  $y = 0 \cdot x + 4 = 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. den Punkt $Q (2 | 5)$ geht und parallel ist zur Winkelhalbierenden des 2.Quadranten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur Winkelhalbierenden des 2. Quadranten bedeutet gleiche Steigung.
  Die Steigung der Winkelhalbierenden des 2. Quadranten ist -1
  $\Rightarrow m = - 1$
  $m$ in die Geradengleichung einsetzen und damit $t$ berechnen.
  $\begin{array}{rcl} 5 & = & - 2 + t & | + 2 \\ t & = & 7 \end{array}$
  $m$ und $t$ in die allgemeine Geradengleichung einsetzen.
  $y = - 1 \cdot x + 7 = - x + 7$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. den Punkt $R (- 4 | 2)$ geht und parallel ist zur $y$ -Achse.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur $y$ -Achse, d.h. keine Funktionsgleichung, da einem $x$ -Wert unendlich viele $y$ -Werte zugeordnet werden. Die Gerade kann also nur als der $x$ -Wert von $R$ beschrieben werden.
  $\Rightarrow x = - 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. den Punkt $S (2 | - 3)$ geht und parallel ist zur Winkelhalbierenden des 1.Quadranten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur Winkelhalbierenden des 1. Quadranten bedeutet die gleiche Steigung.
  Die Steigung der Winkelhalbierenden des 1. Quadranten ist 1.
  $\Rightarrow m = 1$
  Setze m und S in die allgemeine Geradengleichung ein und löse nach $t$ auf.
  $\begin{array}{rcl} - 3 & = & 2 + t & | - 2 \\ t & = & - 5 \end{array}$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  $\Rightarrow y = x - 5$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. den Ursprung geht und parallel ist zur Geraden $AB$ mit $A (- 72 | - 60)$ und $B (- 24 | - 20)$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Durch den Ursprung, das heißt $y$ -Achsenabschnitt $t = 0$
  Parallel zur Geraden $AB$ , bedeutet die gesuchte Gerade hat die gleiche Steigung wie $AB$ .
  $A (- 72 | - 60); B (- 24 | - 20)$
  Berechne die Steigung $m$ mithilfe des Differenzenquotienten .
  $m = \frac{- 20 - (- 60)}{- 24 - (- 72)} = \frac{40}{48} = \frac{5}{6}$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  $\Rightarrow y = \frac{5}{6} x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10
Bestimme die Gleichung der Geraden g, die parallel zur Geraden h ist und durch den Punkt P geht.
1. h: $y = 3 x - 2$ ; P(1|0)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y = 3 x - 2$ ; P(1|0)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m = 3$
  Geradengleichung aufstellen
  Setze m (3) und P(1|0) in die allgemeinen Geradengleichung ein.
  $0$ $=$ $3 \cdot 1 + t$ $- 3$
  ↓
  Gleichung nach t auflösen.
  $t$ $=$ $- 3$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\Rightarrow$ Geradengleichung: $y = 3 x - 3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. h: $y = x - 4$ ; P(1|2)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y = x - 4$ ; P(1|2)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m = 1$
  Gleichung aufstellen
  Setze m (1) und P(1|2) in die allgemeinen Geradengleichung ein.
  $2$ $=$ $1 + t$ $ - 1$
  ↓
  Gleichung nach t auflösen.
  $ t$ $=$ $1$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\Rightarrow$ Geradengleichung: $y = x + 1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. h: $y = 4 x$ ; P(5|18)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y = 4 x$ ; P(5|18)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m = 4$
  Gleichung aufstellen
  Setze m (4) und P(5|18) in die allgemeinen Geradengleichung ein.
  $18$ $=$ $4 \cdot 5 + t$ $- 20$
  ↓
  Gleichung nach t auflösen.
  $t$ $=$ $- 2$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\Rightarrow$ Geradengleichung: $y = 4 x - 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. h: $y = - 2 x + 1$ ; P(-1|4)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y = - 2 x + 1$ ; P(-1|4)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m = - 2$
  Gleichung aufstellen
  Setze m (-2) und P(-1|4) in die allgemeinen Geradengleichung ein.
  $4$ $=$ $- 2 \cdot (- 1) + t$ $- 2$
  ↓
  Gleichung nach t auflösen.
  $t$ $=$ $2$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\Rightarrow$ Geradengleichung: $y = - 2 x + 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
11
Zeige rechnerisch, dass sich die drei Geraden $g_{1}$ : $y = 0,5 x$ ; $g_{2}$ : $y = x - 1,5$ ; $g_{3}$ : $y = - 2 x + 7,5$ in genau einem Punkt schneiden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Geraden
Schnittpunkt zweier Geraden
$g_{2}$ : $y = x - 1,5$ ; $g_{3} :$ $y = - 2 x + 7,5$
Es ist hier zu empfehlen, zunächst den Schnittpunkt von zwei Geraden zu berechnen und dann zu prüfen, ob der Schnittpunkt auch ein Punkt auf der anderen Gerade ist.
Zwei der drei Geraden werden gleichgesetzt, um die x-Koordinate des Schnittpunktes zu berechnen.
$x - 1,5$ $=$ $- 2 x + 7,5$
↓
Addiere zunächst 2x und anschließend 1,5.
$3 x$ $=$ $9$
↓
Dividiere durch 3.
$x$ $=$ $3$
Den x-Wert in eine der beiden gleichgesetzten Geraden einsetzen (z. B. $g_{2}$ ), um die y-Koordinate des Schnittpunktes von $g_{2}$ und $g_{3}$ zu berechnen.
$y = 3 - 1,5 = 1,5$
$\Rightarrow$ $S (3 | 1,5)$
Gerade überprüfen
$g_{1}$ : $y = 0,5 x$
Der Schnittpunkt wird nun in $g_{1}$ eingesetzt. Das heißt, dass $x$ und $y$ der Gerade $g_{1}$ durch 3 und 1,5 ersetzt werden.
$1,5 = 0,5 \cdot 3$
Prüfe ob die so entstandene Aussage wahr ist, um festzustellen, ob $g_{1}$ durch $S$ läuft.
$1,5 = 1,5$
$\Rightarrow$ Dies ist eine wahre Aussage, also ist $S$ der gemeinsame und einzige Schnittpunkt aller drei Geraden.

Berechne den Schnittpunkt der Geradenpaare.

Gib den Schnittpunkt in das Eingabefeld ein, zum Beispiel so: "S(4|-5)" oder "S(4;-5)"

Wenn es keinen Schnittpunkt gibt, gib "-" ein.

$y = 3 x + 4$ und $y = - 2 x + 14$

$y = 6 x - 3$ und $y = 7 x - 11$

$y = 8 x + 3$ und $y = - 4 x + 6$

$y = 7 x - 14$ und $y = 7 x - 3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte von Funktionen berechnen
Geraden mit gleicher Steigung (hier 7) schneiden sich nicht, denn sie sind parallel zueinander.Setzt man die Funktionsterme gleich, so erhält man eine falsche Aussage, also keinen Schnittpunkt.
$7 x - 14$ $=$ $7 x - 3$ $- 7 x$
$- 14$ $=$ $- 3$
↓
falsche Aussage!
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$y = \frac{1}{6} x - 4$ und $y = \frac{1}{3} x - 10$

$y = \frac{1}{2} x + \frac{3}{2}$ und $y = \frac{1}{2}$

13
Bestimme von folgenden Geraden die Schnittpunkte mit den Koordinatenachsen.
1. $y = - 2 x + 3,5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
  Schnittpunkt mit der x-Achse
  Berechne den Schnittpunkt der Geraden mit der x-Achse.
  Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach $x$ auf.
  $\begin{array}{rcll} 0 & = & - 2 x + 3,5 & | + 2 x \\ 2 x & = & 3,5 & | : 2 \\ x & = & 1,75 \end{array}$
  $\Rightarrow$ Die Gerade schneidet die x-Achse bei $S_{x} (1,75 | 0)$ .
  Schnittpunkt mit der y-Achse
  Berechne den Schnittpunkt der Geraden mit der y-Achse.
  Setze dazu in den Ausdruck für die Geradengleichung den Wert $x = 0$ ein.
  $y = - 2 \cdot 0 + 3,5$
  $y = 3,5$
  $\Rightarrow$ Die Gerade schneidet die y-Achse bei $S_{y} (0 | 3,5)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $y = 5 x - 7$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
  Schnittpunkt mit der x-Achse
  Berechne den Schnittpunkt der Geraden mit der x-Achse.
  Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach $x$ auf.
  $\begin{array}{rcll} 0 & = & 5 x - 7 & | + 7 \\ 5 x & = & 7 & | : 5 \\ x & = & \frac{7}{5} = 1,4 \end{array}$
  $\Rightarrow$ Die Gerade schneidet die x-Achse bei $S_{x} (1,4 | 0)$ .
  Schnittpunkt mit der y-Achse
  Berechne den Schnittpunkt der Geraden mit der y-Achse.
  Setze dazu in den Ausdruck für die Geradengleichung den Wert $x = 0$ ein.
  $y = 5 \cdot 0 - 7$
  $y = - 7$
  $\Rightarrow$ Die Gerade schneidet die y-Achse bei $S_{y} (0 | - 7)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $y = \frac{3}{2} x + 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
  Schnittpunkt mit der x-Achse
  Berechne den Schnittpunkt der Geraden mit der x-Achse.
  Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach $x$ auf.
  $\begin{array}{rcll} 0 & = & \frac{3}{2} x + 2 & | - 2 \\ \frac{3}{2} x & = & - 2 & | \cdot \frac{2}{3} \\ x & = & - \frac{4}{3} \end{array}$
  $\Rightarrow$ Die Gerade schneidet die x-Achse bei $S_{x} (- \frac{4}{3} | 0)$ .
  Schnittpunkt mit der y-Achse
  Berechne den Schnittpunkt der Geraden mit der y-Achse.
  Setze dazu in den Ausdruck für die Geradengleichung den Wert $x = 0$ ein.
  $y = \frac{3}{2} \cdot 0 + 2$
  $y = 2$
  $\Rightarrow$ Die Gerade schneidet die y-Achse bei $S_{y} (0 | 2)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $y = - \frac{2}{5} x + \frac{5}{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
  Schnittpunkt mit der x-Achse
  Berechne den Schnittpunkt der Geraden mit der x-Achse.
  Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach $x$ auf.
  $\begin{array}{rcll} 0 & = & - \frac{2}{5} x + \frac{5}{2} & | + \frac{2}{5} x \\ \frac{2}{5} x & = & \frac{5}{2} & | \cdot \frac{5}{2} \\ x & = & \frac{25}{4} = 6,25 \end{array}$
  $\Rightarrow$ Die Gerade schneidet die x-Achse bei $S_{x} (6,25 | 0)$ .
  Schnittpunkt mit der y-Achse
  Berechne den Schnittpunkt der Geraden mit der y-Achse.
  Setze dazu in den Ausdruck für die Geradengleichung den Wert $x = 0$ ein.
  $y = - \frac{2}{5} \cdot 0 + \frac{5}{2}$
  $y = \frac{5}{2} = 2,5$
  $\Rightarrow$ Die Gerade schneidet die y-Achse bei $S_{y} (0 | 2,5)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $y = 2 (x - \frac{2}{3})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
  Klammer auflösen
  Um eine allgemeine Geradengleichung $y = m \cdot x + t$ zu erhalten, multipliziere die Klammer aus.
  $y = 2 (x - \frac{2}{3})$
  $y = 2 x - \frac{4}{3}$
  Schnittpunkt mit der x-Achse
  Berechne den Schnittpunkt der Geraden mit der x-Achse.
  Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach $x$ auf.
  $\begin{array}{rcll} 0 & = & 2 x - \frac{4}{3} & | + \frac{4}{3} \\ 2 x & = & \frac{4}{3} & | : 2 \\ x & = & \frac{2}{3} \end{array}$
  $\Rightarrow$ Die Gerade schneidet die x-Achse bei $S_{x} ( \frac{2}{3} | 0)$ .
  Schnittpunkt mit der y-Achse
  Berechne den Schnittpunkt der Geraden mit der y-Achse.
  Setze dazu in den Ausdruck für die Geradengleichung den Wert $x = 0$ ein und löse nach $x$ auf.
  $y = 2 \cdot 0 - \frac{4}{3}$
  $y = - \frac{4}{3}$
  $\Rightarrow$ Die Gerade schneidet die y-Achse bei $S_{y} (0 | - \frac{4}{3})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $y = - \frac{4}{3} - \frac{1}{2} x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
  Gleichung umstellen
  Um eine allgemeine Geradengleichung $y = m \cdot x + t$ zu erhalten, vertausche auf der rechten Seite beide Elemente.
  $y = - \frac{4}{3} - \frac{1}{2} x$
  $= - \frac{1}{2} x - \frac{4}{3}$
  Schnittpunkt mit der x-Achse
  Berechne den Schnittpunkt der Geraden mit der x-Achse.
  Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach $x$ auf.
  $\begin{array}{rcll} 0 & = & - \frac{4}{3} - \frac{1}{2} x & | + \frac{1}{2} x \\ \frac{1}{2} x & = & - \frac{4}{3} & | \cdot 2 \\ x & = & - \frac{8}{3} = - 2 \frac{2}{3} \end{array}$
  $\Rightarrow$ Die Gerade schneidet die x-Achse bei $S_{x} ( - \frac{8}{3} | 0)$ .
  Schnittpunkt mit der y-Achse
  Berechne den Schnittpunkt der Geraden mit der y-Achse.
  Setze dazu in den Ausdruck für die Geradengleichung den Wert $x = 0$ ein.
  $y = - \frac{1}{2} \cdot 0 - \frac{4}{3}$
  $y = - \frac{4}{3}$
  $\Rightarrow$ Die Gerade schneidet die y-Achse bei $S_{y} (0 | - \frac{4}{3})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
14
Stelle die Funktionsgleichung für die Gerade durch die Punkte P(-25|30) und Q(55|-30) auf und berechne den Schnittpunkt der Gerade mit der x-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung ermitteln
P(-25|30); Q(55|-30)
Ermittle die Steigung m der allgemeinen Geradengleichung mithilfe des Differenzenqotienten .
$m = \frac{30 - (- 30)}{- 25 - 55} = \frac{60}{- 80} = - \frac{3}{4}$
Setze m und die Koordinaten eines Punktes z. B. P(-25|30) in die allgemeine Geradengleichung ein.
$30 = \frac{- 3}{4} (- 25) + t$
Vereinfache: $\frac{- 3}{4} (- 25) = \frac{- 3 (- 25)}{4} = \frac{3 \cdot 25}{4} = \frac{75}{4}$
$30$ $=$ $\frac{75}{4} + t$ $- \frac{75}{4}$
↓
Löse nach t auf.
$t$ $=$ $30 - \frac{75}{4}$
$t$ $=$ $\frac{45}{4}$
↓
Setze m und t in die allgemeine Geradengleichung ein.
$\Rightarrow y = - \frac{3}{4} x + \frac{45}{4}$
Schnittpunkt mit der x-Achse
An der Schnittstelle mit der x-Achse ist der y-Wert 0.
$0 = \frac{- 3}{4} x + \frac{45}{4}$
Nach x auflösen. Stelle dafür das x alleine durch: $| \cdot \frac{- 4}{3}$
Beachte, dass bei beide Summanden multipliziert werden müssen.
$0 = \frac{(- 3) (- 4)}{4 \cdot 3} x + \frac{45 (- 4)}{4 \cdot 3}$
$\frac{(- 3) (- 4)}{4 \cdot 3} = \frac{3 \cdot 4}{12} = \frac{12}{12} = 1$
$0 = x + \frac{- 180}{12}$
$0 = x - 15$
Addiere 15
$x = 15$
$\Rightarrow$ Die Gerade schneidet die x-Achse bei S(15|0).

Zeigen Sie: Die Gerade g durch $P_{1} (\sqrt{k} / k)$ und $P_{2} (1 / 1)$ besitzt die Steigung $a_{1} = \sqrt{k} + 1$ und schneidet die y-Achse in $P_{y} (0 / - \sqrt{k})$

16
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Ermitteln Sie den Funktionsterm der linearen Funktion $f (x)$ , wenn gilt:
1. $f (1) = 7; f (- 1) = 3$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
  $f (x) = m \cdot x + t$
  Setze $f (1)$ und $f (- 1)$ in die allgemeine Geradengleichung ein.
  $\begin{array}{l} 1) 7 = m \cdot 1 + t \\ 2) 3 = m \cdot (- 1) + t \end{array}$
  Löse das Gleichungssystem auf.
  $1) + 2) : 10 = 2 t | : 2$
  $\Rightarrow t = 5$
  Setze t in 1) ein.
  $7 = m + 5 | - 5$
  $m = 2$
  Setze m und t in die allgemeine Geradengleichung ein.
  $f (x) = 2 x + 5$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (a) = 0; f (0) = a$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
  $f (x) = m \cdot x + t$
  t ist der y-Achsenabschnitt, also der Wert bei x=0.
  $t = f (0) = a$
  Setze das und f(a)=0 in die allgemeine Geradengleichung ein.
  $0 = m \cdot a + a$
  Löse nach m auf.
  $m = \frac{- a}{a} = - 1$
  Setze m = -1 und t = a in die allgemeine Funktionsgleichung ein.
  $f (x) = - x + a$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (a) = 1; f (2 a) = - 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
  $f (x) = m \cdot x + t$
  Setze $f (a)$ und $f (2 a)$ in die allgemeine Geradengleichung ein.
  $\begin{array}{rrclcr} I & 1 & = & m \cdot a & + & t \\ II & - 1 & = & m \cdot 2 a & + & t \end{array}$
  Löse das Gleichungssystem auf.
  $\begin{array}{l} 2 \cdot I - II : \\ 2 - (- 1) = 2 t - t \end{array}$
  $\Rightarrow t = 3$
  Setze t in $I$ ein.
  $1 = m \cdot a + 3$
  Löse die Gleichung nach m auf.
  $m = (1 - 3) \cdot \frac{1}{a} = - \frac{2}{a}$
  Setze $m = - \frac{2}{a}$ und $t = 3$ in die allgemeine Geradengleichung ein.
  $f (x) = - \frac{2}{a} \cdot x + 3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
17
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Für eine lineare Funktion $h (x)$ gilt:
$h (0) = 3$ und $h (- 2) = 4$ . Bestimmen Sie $h (x)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
Bestimme den y-Achsenabschnitt t
Bei einer Funktion ist der y-Achsenabschnitt gleich dem Wert bei x=0.
$t = h (0) = 3$
Bestimme jetzt mit den zwei gegebenen Punkten die Steigung m mit dem Differenzenquotienten.
$m = \frac{3 - 4}{0 - (- 2)} = \frac{- 1}{2} = - \frac{1}{2}$
Setze zur Geradengleichung zusammen.
$\Rightarrow y = - \frac{1}{2} x + 3$
18
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Eine Gerade durch $P (2,5 | 0)$ schließt mit den Koordinatenachsen ein Dreieck ein.
Für welche Steigung ist dieses Dreieck gleichschenklig?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Dreieck
Zwei Seiten des Dreiecks sind Koordinatenachsen. Diese haben einen rechten Winkel zwischen sich, das Dreieck ist also sicher rechtwinklig. Der rechte Winkel kann kein Basiswinkel im gleichschenkligen Dreieck sein, also sind die gleichlangen Schenkel die Katheten (Achsen).
Es gibt zwei Möglichkeiten einen Punkt zu wählen, dass die Katheten gleichlang sind: $Q_{1} (0 | 2,5)$ und $Q_{2} (0 | - 2,5)$ . Das Dreieck liegt dann im 1. Quadranten oder im 4. Quadranten. In anderen Quadranten kann das Dreieck nicht liegen, da P auf der Grenze zwischen dem ersten und vierten liegt.
Damit erhältst du ein Steigungsdreieck für $Q_{1}$ mit der Steigung $- 1$ und eines für $Q_{2}$ mit der Steigung $1$ .
Ein solches Dreieck tritt also für die Steigungen $m_{1} = - 1$ und $m_{2} = 1$ auf.

Bestimme für welche x-Werte $f (x) > 0$ gibt.

$f (x) = 0,4 x + 1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ungleichungen lösen
$f (x)$ $>$ $0$
↓
Setze den Funktionsterm ein.
$0,4 x + 1$ $>$ $0$ $- 1$
↓
Sortiere nach x-Termen und Zahlen.
$0,4 x$ $>$ $- 1$ $: 0,4$
↓
Löse nach $x$ auf (beachte $0,4 > 0$ , also bleibt das Ungleichheitszeichen).
$x$ $>$ $- \frac{1}{0,4} = - 2,5$
$f (x)$ ist größer Null für alle $x > - 2,5$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = - 1,5 (x - 2)$

$f (x) = \frac{x}{5} - \frac{7}{5}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ungleichungen lösen
$f (x)$ $>$ $0$
↓
Funktionsgleichung einsetzen.
$\frac{x}{5} - \frac{7}{5}$ $>$ $0$ $+ \frac{7}{5}$
↓
Sortiere nach x-Termen und Zahlen.
$\frac{x}{5}$ $>$ $\frac{7}{5}$ $\cdot 5$
↓
Nach x auflösen (5>0, also keine Änderung am Ungleichungszeichen)
$x$ $>$ $7$
Für $x > 7$ ist $f (x)$ positiv.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

20
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Prüfen Sie, ob die Gerade durch $P_{1}$ und $P_{2}$ eine Ursprungsgerade ist.
1. $P_{1} (2 | 4); P_{2} (- 1,5 | - 3)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
  Setze die beiden Punkte in die allgemeine Geradengleichung ein:
  $y = mx + t$
  $\begin{aligned} 1) & 4 & = & 2 m + t \\ 2) & - 3 & = & - 1,5 m + t & | \cdot (- 1) \end{aligned}$
  $\begin{aligned} 1) & 4 & = & 2 m + t \\ 2) & 3 & = & 1,5 m - t \end{aligned}$
  Wende das Additionsverfahren an.
  Berechne $1) + 2)$ .
  $7$ $=$ $3,5 m$ $: 3,5$
  $m$ $=$ $\frac{7}{3,5}$
  $m$ $=$ $2$
  Setze m in eine der beiden Funktionen ein.
  $4$ $=$ $2 \cdot 2 + t$
  $4$ $=$ $4 + t$ $- 4$
  $t$ $=$ $4 - 4$
  $t$ $=$ $0$
  $y = 2 x$
  Die Gerade durch $P_{1}$ und $P_{2}$ ist eine Ursprungsgerade, da für $x = 0$ der y-Wert gleich $0$ ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $P_{1} (- 1 | 3,5); P_{2} (2 | - 2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
  Setze die beiden Punkte in die allgemeine Geradengleichung ein:
  $y = m x + t$
  $\begin{array}{l} 1) 3,5 = - 1 m + t \\ 2) - 2 = 2 m + t \end{array}$
  Löse das lineare Gleichungssysten zum Beispiel mit dem Additionsverfahren.
  Multipliziere dafür zunächst die Gleichung $1)$ auf beiden Seiten mit $(- 1)$
  $\begin{array}{l} 1) - 3,5 = m - t \\ 2) - 2 = 2 m + t \end{array}$
  Berechne $1) + 2)$
  $- 5,5$ $=$ $3 m$
  $- \frac{11}{2}$ $=$ $3 m$ $: 3$
  $- \frac{11}{2 \cdot 3}$ $=$ $m$
  $- \frac{11}{6}$ $=$ $m$
  Setze $m$ in eine der beiden Gleichungen ein
  $- 2$ $=$ $2 \cdot (- \frac{11}{6}) + t$
  $- 2$ $=$ $- \frac{11}{3} + t$ $+ \frac{11}{3}$
  $- \frac{6}{3} + \frac{11}{3}$ $=$ $t$
  $- \frac{5}{3}$ $=$ $t$
  Setze m und t in die allgemeine Geradengleichung.
  $m = - \frac{11}{6}; t = \frac{5}{3}$
  $y = - \frac{11}{6} \cdot x + \frac{5}{3}$
  Die Gerade durch $P_{1}$ und $P_{2}$ ist keine Ursprungsgerade, da für $x = 0$ der y-Wert gleich $\frac{5}{3}$ ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
21
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Zwei Geraden $f (x)$ und $g (x)$ schneiden sich auf der x-Achse in x=4.
Bestimmen Sie mögliche Funktionsterme.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Für diese Aufgabe gibt es keine eindeutige Lösung. Gesucht sind zwei verschiedenen lineare Funktionen, die beide durch den Punkt (4|0) laufen.
Ein sehr einfaches Beispiel wäre $f (x) = 0$ , also die x-Achse und $g (x) = x - 4$ . $f (x)$ läuft offensichtlich durch (4|0). Für g(x) lässt sich das auch sehr einfach überprüfen: $g (4) = 4 - 4 = 0$ .
Andere mögliche Funktionen sind: $y = - x + 4$ , $y = 2 x - 8$ (allgemein $y = a x - 4 a$ für beliebige a)
Überlege durch welchen Punkt beide Geraden gehen müssen.
Bestimme zwei verschiedene Funktionen, die durch diesen Punkt gehen.
22
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Zeigen Sie: Die Punkte $P (\frac{k}{2} \sqrt{2} | k)$ liegen für alle $k \in ℝ$ auf einer Geraden.
Bestimmen Sie die Geradengleichung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Gegeben ist eine Menge von Punkten $P (\frac{k}{2} \cdot \sqrt{2} | k)$ .
Um die allgemeine Geradengleichung herauszufinden, brauchen wir 2 Punkte auf der Gerade. Deshalb wählt man hier am besten z.B. die zwei Punkte $F (\frac{k}{2} \cdot \sqrt{2} | k)$ und
$G (\frac{k + 1}{2} \cdot \sqrt{2} | k + 1)$ .
$y = m \cdot x + t$
Bestimme zuerst die Steigung m.
$m = \frac{k + 1 - k}{\frac{k + 1}{2} \cdot \sqrt{2} - \frac{k}{2} \cdot \sqrt{2}} = \frac{1}{\frac{\sqrt{2}}{2}} = \frac{2}{\sqrt{2}}$
Nun kann man m und einen der Punkte, z.B. hier am Besten gleich P, in die allgemeine Geradengleichung einsetzen.
$k = \underset{= k}{\underset{⏟}{\frac{k}{2} \cdot \sqrt{2} \cdot \frac{2}{\sqrt{2}}}} + t$
Löse nach t auf.
$\Rightarrow t = 0$
Gebe die Geradengleichung an.
$y = \frac{2}{\sqrt{2}} \cdot x$
23
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Prüfe, ob die Geraden $g, h, i$ durch einen Punkt verlaufen.
1. $g (x) = x + 1; h : 2 y + x + 4 = 0; i : 3 y - 5 x = 7$
  Ja sie verlaufen durch einen Punkt.
  Nein, sie verlaufen nicht durch einen Punkt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt von Geraden
  Bringe zuerst alle Geraden in die allgeimeine Form $y = m x + t$ .
  Gerade g:
  $g (x) = x + 1$
  $\Leftrightarrow y = x + 1$
  Gerade h:
  $2 y + x + 4 = 0$
  $\Leftrightarrow 2 y = - x - 4$
  $\Leftrightarrow y = - \frac{1}{2} x - 2$
  Gerade i:
  $3 y - 5 x = 7$
  $\Leftrightarrow 3 y = 5 x + 7$
  $\Leftrightarrow y = \frac{5}{3} x + \frac{7}{3}$
  Bestimme den Schnittpunkt von g und h
  Setze dazu die jeweiligen rechten Seiten gleich.
  $x + 1$ $=$ $- \frac{1}{2} x - 2$ $+ \frac{1}{2} x - 1$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $x + \frac{1}{2} x$ $=$ $- 2 - 1$
  ↓
  Fasse zusammen.
  $\frac{3}{2} x$ $=$ $- 3$ $: \frac{3}{2}$
  $x$ $=$ $- 2$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = - 2 + 1 = - 1$
  Der Schnittpunkt ist $S_{g h} (- 2 | - 1) .$
  Bestimme den Schnittpunkt von g und i
  Setze dazu die jeweiligen rechten Seiten gleich.
  $x + 1$ $=$ $\frac{5}{3} x + \frac{7}{3}$ $- \frac{5}{3} x - 1$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $x - \frac{5}{3} x$ $=$ $\frac{7}{3} - 1$
  ↓
  Fasse zusammen.
  $- \frac{2}{3} x$ $=$ $\frac{4}{3}$ $: (- \frac{2}{3})$
  $x$ $=$ $- 2$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = - 2 + 1 = - 1$
  Der Schnittpunkt ist $S_{g i} (- 2 | - 1) .$
  Da sich $g$ mit $h$ und mit $i$ im selben Punkt schneidet, schneiden sich auch $h$ und $i$ in diesem Punkt. Die Geraden laufen also alle durch den Punkt $(- 2 | - 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $g (x) = \frac{1}{6} x + \frac{3}{2}; h (x) = - \frac{2}{3} x + 2; i : 2 x - y = 3$
  Ja sie verlaufen durch einen Punkt.
  Nein, sie verlaufen nicht durch einen Punkt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt von Geraden
  Bringe zuerst alle Geraden in die allgeimeine Form $y = m x + t$ .
  Gerade g:
  $g (x) = \frac{1}{6} x + \frac{3}{2}$
  $\Leftrightarrow y = \frac{1}{6} x + \frac{3}{2}$
  Gerade h:
  $h (x) = - \frac{2}{3} x + 2$
  $\Leftrightarrow y = - \frac{2}{3} x + 2$
  Gerade i:
  $2 x - y = 3$
  $\Leftrightarrow y = 2 x - 3$
  Bestimme den Schnittpunkt von g und h
  Setze dazu die jeweiligen rechten Seiten gleich.
  $\frac{1}{6} x + \frac{3}{2}$ $=$ $- \frac{2}{3} x + 2$ $+ \frac{2}{3} x - \frac{3}{2}$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $\frac{1}{6} x + \frac{2}{3} x$ $=$ $2 - \frac{3}{2}$
  ↓
  Fasse zusammen.
  $\frac{5}{6} x$ $=$ $\frac{1}{2}$ $: \frac{5}{6}$
  $x$ $=$ $\frac{3}{5}$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = \frac{1}{6} \cdot \frac{3}{5} + \frac{3}{2}$
  $= \frac{1}{10} + \frac{3}{2} = \frac{16}{10}$
  $= \frac{8}{5}$
  Der Schnittpunkt ist $S_{g h} (\frac{3}{5} | \frac{8}{5}) .$
  Bestimme den Schnittpunkt von g und i
  Setze dazu die jeweiligen rechten Seiten gleich.
  $\frac{1}{6} x + \frac{3}{2}$ $=$ $2 x - 3$ $- 2 x - \frac{3}{2}$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $\frac{1}{6} x - 2 x$ $=$ $- 3 - \frac{3}{2}$
  ↓
  Fasse zusammen.
  $- \frac{11}{6} x$ $=$ $- \frac{9}{2}$ $: (- \frac{11}{6})$
  $x$ $=$ $\frac{9}{2} \cdot \frac{6}{11} = \frac{27}{11}$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = \frac{1}{6} \cdot \frac{27}{11} + \frac{3}{2}$
  $= \frac{9}{22} + \frac{3}{2} = \frac{42}{22}$
  $= \frac{21}{11}$
  Der Schnittpunkt ist $S_{g i} (\frac{27}{11} | \frac{21}{11}) .$
  Damit schneidet die Gerade $g$ die Gerade $h$ in einem anderen Punkt als die Gerade $i$ . Also laufen die Geraden nicht durch einen Punkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
24
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Zwei aufeinander senkrecht stehende Geraden schneiden sich in $S (- 2 | - 1)$ .
Geben Sie mögliche Geradengleichungen an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Wir haben zwei zueinander senkrechte Geraden mit dem Schnittpunkt $(- 2, - 1)$ . Wie man aus der Angabe schon rauslesen kann, gibt es mehrere Möglichkeiten, zwei solcher Geraden zu wählen. Im Folgenden wird eine Möglichkeit angegeben. Ein gutes Kriterium, um zu überprüfen, ob die zwei gewählten Geraden senkrecht zueinander sind, ist folgendes:
$m_{1} \cdot m_{2} = - 1$ .
Wähle zum Beispiel die Geraden g mit $y = g (x) = x + 1$ und h mit $y = h (x) = - x - 3$ . Dann gilt $m_{1} \cdot m_{2} = 1 \cdot (- 1) = - 1$ und es gilt $g (- 2) = - 1$ und $h (- 2) = - 1$ . Also liegt der Schnittpunkt auf den beiden Geraden und diese sind senkrecht zueinander.
Achtung:
Wählst du zum Beispiel die Gerade $y = - 1$ (eine Parallele zur x-Achse), die durch den Punkt $(- 2, - 1)$ geht, gibt es genau eine Gerade, nämlich die Gerade, die parallel zur y-Achse steht mit der Geradengleichung $x = - 2$ . Diese stehen zwar senkrecht aufeinander, aber $x = - 2$ ist keine Funktion, sondern eine Relation.

Forme die Gleichung so um, dass sie die Form $y = ax + b$ hat.

$2 x - y = 6$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
$2 x - y$ $=$ $6$ $- 2 x$
$- y$ $=$ $6 - 2 x$ $\cdot (- 1)$
$y$ $=$ $2 x - 6$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$x = \frac{1}{2} (y + 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
$x$ $=$ $\frac{1}{2} (y + 1)$ $\cdot 2$
↓
Der Bruch auf der rechten Seite fällt weg da $\frac{1}{2} \cdot 2 = 1$ .
$2 x$ $=$ $y + 1$ $- 1$
↓
Linke und rechte Seite vertauschen.
$y$ $=$ $2 x - 1$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\frac{2}{5} y = 2 x - 1$

$y = 3 (2 x - 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
$y$ $=$ $3 (2 x - 1)$
↓
Die Klammer ausmultiplizieren.
$y$ $=$ $6 x - 3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

26
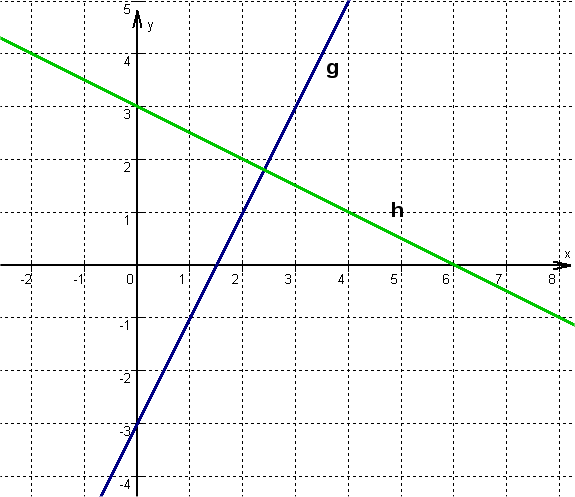
Gegeben sind die Geraden $g : y = 2 x - 3$ und $h : y = - 0,5 x + 3$ .
1. Überprüfe, ob die Punkte $A (1 | - 1)$ , $B (0,5 | 1,5)$ , $C (- 6 | 5)$ , $D (- 102 | 55)$ und $E (45 | 87)$ auf einer der Geraden liegen.
  $A$ liegt auf einer der Geraden.
  $B$ liegt auf keiner der Geraden.
  $C$ liegt auf keiner der Geraden.
  $D$ liegt auf einer der Geraden.
  $E$ liegt auf einer der Geraden.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Überprüfung mit Skizze
  Wähle jeweils einen beliebigen Punkt auf der Geraden, z. B. die y-Achsenabschnitte $(0 | - 3)$ und $(0 | 3)$ . Gehe von dort $1$ nach rechts und entsprechen der Steigungen $m_{g} = 2$ nach oben und $m_{h} = - 0,5$ nach unten. Verbinde jeweils die beiden Punkte zu einer Geraden.
  Wenn du den Verlauf der Geraden betrachtest und beispielsweise die Lage des Punktes $A$ , so siehst du, dass dieser kaum auf der Geraden h, wahrscheinlich aber auf $g$ liegen wird. Ähnlich kannst du bei anderen Punkten entscheiden, ob sich eine rechnerische Überprüfung lohnt: Punkt $D (- 102 / 55)$ kann z. B. nur auf $h$ liegen.
  Rechnerische Überprüfung
  $A (1 | - 1)$ in $g$ einsetzen:
  Setze die Koordinaten der Punkte in die fragliche Gleichung ein. Also setze $y = - 1$ und $x = 1$ ein.
  $- 1 = 2 \cdot 1 - 3$
  Das ist eine wahre Aussage.
  ⇒ $A$ liegt auf $g$ .
  $B$ liegt auf keiner der Geraden. Das kann eindeutig der Skizze entnommen werden.
  $C$ in $h$ einsetzen:
  $5 = - 0,5 \cdot (- 6) + 3$
  ⇒ $5 = 3 + 3$
  Diese Aussage ist falsch, also liegt $C$ nicht auf $h .$
  $D$ in $h$ einsetzen:
  $55 = - 0,5 \cdot (- 102) + 3$
  ⇒ $55 = 51 + 3$
  Diese Aussage ist falsch, also liegt $D$ nicht auf $h$ .
  $E$ in $g$ einsetzen:
  $87 = 2 \cdot 45 - 3$
  Diese Aussage ist richtig, also liegt $E$ auf $g$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ergänze die Koordinaten so, dass die Punkte auf h liegen: P(5 | ?) , Q(-3,5 | ?) , R(? | 12) , S(? | -7,5).
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Koordinaten ergänzen
  $h : y = - 0,5 x + 3$ ; P(5|?)
  Die gegebene Koordinate des Punktes (die x-Koordinate) wird in die Funktionsgleichung eingesetzt und daraus die fehlende y-Koordinate berechnet.
  $y = - 0,5 \cdot 5 + 3 = - 2,5 + 3 = 0,5$
  ⇒ P(5|0,5)
  Q: $y = - 0,5 \cdot (- 3,5) + 3 = 1,75 + 3 = 4,75$ $\Rightarrow$ Q(-3,5|4,75)
  R: $12 = - 0,5 x + 3 \Rightarrow 0,5 x = - 9 \Rightarrow x = - 18$ $\Rightarrow$ R(-18|12)
  S: $- 7,5 = - 0,5 x + 3 \Rightarrow 0,5 x = 10,5 \Rightarrow x = 21$ $\Rightarrow$ S(2 1|-7,5).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Zeige, dass T(2,4|1,8) auf beiden Geraden liegt. Was bedeutet dies?
  $T$ liegt auf beiden Geraden. Das hat nichts zu bedeuten.
  $T$ liegt gar nicht auf beiden Geraden.
  $T$ liegt auf beiden Geraden. Damit muss $T$ ein Schnittpunkt sein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Beweis für T
  T(2,4|1,8)
  Die Koordinaten von T in beide Geradengleichungen einsetzen. Wenn die Aussagen wahr sind, liegt T auf den Geraden.
  in g:
  $1,8$ $=$ $2 \cdot 2,4 - 3$
  $1,8$ $=$ $4,8 - 3$
  $1,8$ $=$ $1,8$
  in h:
  $1,8$ $=$ $- 0,5 \cdot 2,4 + 3$
  $1,8$ $=$ $- 1,2 + 3$
  $1,8$ $=$ $1,8$
  $\Rightarrow$ Beide Gleichungen ergeben richtige Aussagen, also liegt der Punkt T auf beiden Geraden.
  $\Rightarrow$ T Ist der Schnittpunkt der Geraden
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
27
Löse die folgenden Aufgaben.
1. Welche Steigung hat die Gerade durch die Punkte $P (0 | 3)$ und $Q (2 | - 3)$ ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: allgemeine Geradengleichung
  Gegeben: Punkt $P (0 | 3)$ und Punkt $Q (2 | - 3)$
  Setze die x-Werte (erste Koordinate) und die y-Werte (zweite Koordinate) in die allgemeine Geradengleichung ein.
  $3 = m \cdot 0 + t$
  $- 3 = m \cdot 2 + t$
  Bei der ersten Gleichung kannst du sofort ablesen, dass $t = 3$ . Dieses $t$ kannst du in die zweite Gleichung einsetzen, um $m$ auszurechnen.
  $- 3$ $=$ $m \cdot 2 + 3$ $- 3$
  $- 6$ $=$ $m \cdot 2$ $: 2$
  $- 3$ $=$ $m$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  $y = - 3 x + 3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Stelle die Gleichung der Geraden durch die Punkte $P (1 | 3)$ und $Q (3 | - 1)$ auf.
  
  Gegeben: Punkt $P (1 | 3)$ und $Q (3 | - 1)$
  Berechne die Differenz der beiden x-Werte und der beiden y-Werte, um die Steigung zu bestimmen.
  x-Werte: $3 - 1 = 2$
  y-Werte: $- 1 - 3 = - 4$
  Während der x-Wert um $2$ steigt, nimmt der y-Wert um $4$ ab. Dividiere den y-Wert durch den x-Wert, um die Steigung auszurechnen.
  $m = \frac{- 4}{2} = - 2$
  Setze m, den x-Wert und den y-Wert eines der Punkte in die allgemeine Geradengleichung ein, um $t$ zu bestimmen.
  $3$ $=$ $- 2 \cdot 1 + t$
  $3$ $=$ $- 2 + t$ $+ 2$
  $t$ $=$ $5$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein, um die Gleichung der Funktion aufzustellen.
  $y = - 2 x + 5$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$m$	$=$	$\frac{8 - 7}{- 3 - 5}$
	↓	Vereinfache Zähler und Nenner
$m$	$=$	$\frac{1}{- 8}$
$m$	$=$	$- \frac{1}{8}$

$m$	$=$	$\frac{4 - 2}{3 - 1}$
	↓	Vereinfache Zähler und Nenner
$m$	$=$	$\frac{2}{2}$
$m$	$=$	$1$

$m_{d} \cdot m_{g}$	$=$	$- 1$	$: m_{g}$
$m_{d}$	$=$	$\frac{- 1}{m_{g}}$
	↓	Setze die Steigung der Funktion $m_{g}$ (nämlich $- \frac{1}{2}$ ) ein.
$m_{d}$	$=$	$\frac{- 1}{- \frac{1}{2}}$
	↓	Vereinfache die rechte Seite.
$m_{d}$	$=$	$- 2$

$- 3$	$=$	$2 \cdot (0) + t$
	↓	Multipliziere aus .
$t$	$=$	$- 3$
	↓	Setze t und $m_{d}$ in die allgemeine Geradengleichung ein.
$y$	$=$	$2 x - 3$

$2 x - 3$	$=$	$- \frac{1}{2} x + 2$	$+ 3$
$2 x$	$=$	$- \frac{1}{2} x + 5$	$+ \frac{1}{2} x$
$\frac{5}{2} x$	$=$	$5$	$: \frac{5}{2}$
$x$	$=$	$2$

$y$	$=$	$2 x - 3$
	↓	Setze das gefundene x = 2 ein.
$y$	$=$	$2 \cdot 2 - 3$
	↓	Rechne aus.
$y$	$=$	$1$

$d^{2}$	$=$	$2^{2} + 4^{2}$
	↓	Berechne die beiden Potenzen.
$d^{2}$	$=$	$4 + 16$
	↓	Addiere.
$d^{2}$	$=$	$20$
	↓	Ziehe die Wurzel.
$d$	$=$	$\sqrt{20}$

$g (x_{s})$	$=$	$h (x_{s})$
	↓	Setz die Geradengleichungen ein.
$- \frac{4}{3} x_{s}$	$=$	$\frac{3}{4} x_{s} - 5$	$- \frac{3}{4} x_{s}$
	↓	Bringe die Variable $x_{s}$ auf die linke Seite.
$- \frac{25}{12} x_{s}$	$=$	$- 5$	$\cdot (- 1)$
$\frac{25}{12} x_{s}$	$=$	$5$	$: \frac{25}{12}$
$x_{s}$	$=$	$\frac{12}{5}$
	$=$	$2,4$

$0$	$=$	$3 \cdot 1 + t$	$- 3$
	↓	Gleichung nach t auflösen.
$t$	$=$	$- 3$

$18$	$=$	$4 \cdot 5 + t$	$- 20$
	↓	Gleichung nach t auflösen.
$t$	$=$	$- 2$

$x - 1,5$	$=$	$- 2 x + 7,5$
	↓	Addiere zunächst 2x und anschließend 1,5.
$3 x$	$=$	$9$
	↓	Dividiere durch 3.
$x$	$=$	$3$

$y$	$=$	$8 x + 3$
$y$	$=$	$- 4 x + 6$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate des zu berechnen.
$8 x + 3$	$=$	$- 4 x + 6$	$- 3; + 4 x$
$12 x$	$=$	$3$	$: 12$
$x$	$=$	$\frac{3}{12} = \frac{1}{4}$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate des zu berechnen.
$y$	$=$	$8 \cdot \frac{1}{4} + 3$
	↓	Punkt vor Strich beachten
$y$	$=$	$5$
	↓	$\Rightarrow$ Schnittpunkt: S( $\frac{1}{4}$ \| $5$ )

$y$	$=$	$\frac{1}{2} x + \frac{3}{2}$
$y$	$=$	$\frac{1}{2}$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate zu berechnen
$\frac{1}{2} x + \frac{3}{2}$	$=$	$\frac{1}{2}$	$- \frac{3}{2}$
$\frac{1}{2} x$	$=$	$- 1$	$\cdot 2$
$x$	$=$	$- 2$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate zu berechnen
$y$	$=$	$\frac{1}{2}$
	↓	$\Rightarrow$ Schnittpunkt: S(-2 \| 0,5)

$f (x)$	$>$	$0$
	↓	Setze den Funktionsterm ein.
$0,4 x + 1$	$>$	$0$	$- 1$
	↓	Sortiere nach x-Termen und Zahlen.
$0,4 x$	$>$	$- 1$	$: 0,4$
	↓	Löse nach $x$ auf (beachte $0,4 > 0$ , also bleibt das Ungleichheitszeichen).
$x$	$>$	$- \frac{1}{0,4} = - 2,5$

$4$	$=$	$- 2 \cdot (- 1) + t$	$- 2$
	↓	Gleichung nach t auflösen.
$t$	$=$	$2$

$y$	$=$	$3 x + 4$
$y$	$=$	$- 2 x + 14$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate des zu berechnen.
$3 x + 4$	$=$	$- 2 x + 14$	$+ 2 x; - 4$
$5 x$	$=$	$10$	$: 5$
$x$	$=$	$2$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate zu berechnen
$y$	$=$	$3 \cdot 2 + 4$
	↓	Punkt vor Strich beachten
$y$	$=$	$10$
	↓	$\Rightarrow$ Schnittpunkt: S(2\|10)

$y$	$=$	$6 x - 3$
$y$	$=$	$7 x - 11$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate zu berechnen.
$6 x - 3$	$=$	$7 x - 11$	$+ 3; - 7 x$
$- x$	$=$	$- 8$	$: (- 1)$
$x$	$=$	$8$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate zu berechnen.
$y$	$=$	$6 \cdot 8 - 3$
	↓	Punkt vor Strich beachten
$y$	$=$	$45$
	↓	$\Rightarrow$ Schnittpunkt: S(8\|45)

$7 x - 14$	$=$	$7 x - 3$	$- 7 x$
$- 14$	$=$	$- 3$
	↓	falsche Aussage!

$y$	$=$	$\frac{1}{6} x - 4$
$y$	$=$	$\frac{1}{3} x - 10$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate zu berechnen
$\frac{1}{6} x - 4$	$=$	$\frac{1}{3} x - 10$	$- \frac{1}{3} x; + 4$
$- \frac{1}{6} x$	$=$	$- 6$	$: (- \frac{1}{6})$
$x$	$=$	$36$
	↓	Den x-Wert in eine der beiden Koordinaten einsetzen, um die y-Koordinate zu berechnen
$y$	$=$	$\frac{1}{3} \cdot 36 - 10$
	↓	Punkt vor Strich beachten
$y$	$=$	$2$
	↓	$\Rightarrow$ Schnittpunkt: S (36\|2)

$30$	$=$	$\frac{75}{4} + t$	$- \frac{75}{4}$
	↓	Löse nach t auf.
$t$	$=$	$30 - \frac{75}{4}$
$t$	$=$	$\frac{45}{4}$
	↓	Setze m und t in die allgemeine Geradengleichung ein.

$k - 1$	$=$	$ m \sqrt{k} - m + t - t$
	↓	Fasse zusammen.
$k - 1$	$=$	$m (\sqrt{k} - 1)$
	↓	Löse nach m auf.
$m$	$=$	$\frac{k - 1}{\sqrt{k} - 1}$
	↓	Vereinfache mit 3. binomischer Formel ( $k = {\sqrt{k}}^{2})$ .
$m$	$=$	$\frac{(\sqrt{k} + 1) (\sqrt{k} - 1)}{\sqrt{k} - 1}$
$m$	$=$	$\sqrt{k} + 1$
	↓	Setze in 2) ein.
$1$	$=$	$(\sqrt{k} + 1) \cdot 1 + t$
	↓	Nach t auflösen.
$t$	$=$	$1 - (\sqrt{k} + 1)$
$t$	$=$	$- \sqrt{k}$

$f (x)$	$>$	$0$
	↓	Funktionsgleichung einsetzen.
$- 1,5 (x - 2)$	$>$	$0$
	↓	Klammer auflösen.
$- 1,5 x + 3$	$>$	$0$	$- 3$
	↓	Nach $x$ -Termen und Zahlen sortieren.
$- 1,5 x$	$>$	$- 3$	$: (- 1,5)$
	↓	Nach $x$ auflösen. Achtung $- 1,5 < 0$ , drehe also das Ungleichheitszeichen.
$x$	$<$	$2$

$f (x)$	$>$	$0$
	↓	Funktionsgleichung einsetzen.
$\frac{x}{5} - \frac{7}{5}$	$>$	$0$	$+ \frac{7}{5}$
	↓	Sortiere nach x-Termen und Zahlen.
$\frac{x}{5}$	$>$	$\frac{7}{5}$	$\cdot 5$
	↓	Nach x auflösen (5>0, also keine Änderung am Ungleichungszeichen)
$x$	$>$	$7$

$4$	$=$	$2 \cdot 2 + t$
$4$	$=$	$4 + t$	$- 4$
$t$	$=$	$4 - 4$
$t$	$=$	$0$

Aufgaben zu linearen Funktionen

Bestimmung der Steigung m

Ermittlung des y-Achsenabschnitts t

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Abstand zweier paralleler Geraden

Skizze

Geradengleichung

Bestimme den Schnittpunkt von d und g

Bestimme den Abstand der Punkte S und T.

Ergebnis

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Geradensteigung und Geradengleichung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Steigung

Funktionsgleichung

Dreiecksfläche

Höhe ermittlen

Grundlinie berechnen

Fläche berechnen

Skizze zur Veranschaulichung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Geradengleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Schnittpunkt mit der x-Achse

Schnittpunkt mit der y-Achse

Hast du eine Frage oder Feedback?

Schnittpunkt mit der x-Achse

Schnittpunkt mit der y-Achse

Hast du eine Frage oder Feedback?

Schnittpunkt mit der x-Achse

Schnittpunkt mit der y-Achse

Hast du eine Frage oder Feedback?

Schnittpunkt mit der x-Achse

Schnittpunkt mit der y-Achse

Hast du eine Frage oder Feedback?

Klammer auflösen

Schnittpunkt mit der x-Achse

Schnittpunkt mit der y-Achse

Hast du eine Frage oder Feedback?

Gleichung umstellen

Schnittpunkt mit der x-Achse

Schnittpunkt mit der y-Achse

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimme den Schnittpunkt von g und h

Bestimme den Schnittpunkt von g und i

Hast du eine Frage oder Feedback?

Bestimme den Schnittpunkt von g und h

Bestimmung der Steigung $m$

Ermittlung des $y$ -Achsenabschnitts $t$

$- 5,5$	$=$	$3 m$
$- \frac{11}{2}$	$=$	$3 m$	$: 3$
$- \frac{11}{2 \cdot 3}$	$=$	$m$
$- \frac{11}{6}$	$=$	$m$

$- 2$	$=$	$2 \cdot (- \frac{11}{6}) + t$
$- 2$	$=$	$- \frac{11}{3} + t$	$+ \frac{11}{3}$
$- \frac{6}{3} + \frac{11}{3}$	$=$	$t$
$- \frac{5}{3}$	$=$	$t$

$x + 1$	$=$	$- \frac{1}{2} x - 2$	$+ \frac{1}{2} x - 1$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$x + \frac{1}{2} x$	$=$	$- 2 - 1$
	↓	Fasse zusammen.
$\frac{3}{2} x$	$=$	$- 3$	$: \frac{3}{2}$
$x$	$=$	$- 2$

$x + 1$	$=$	$\frac{5}{3} x + \frac{7}{3}$	$- \frac{5}{3} x - 1$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$x - \frac{5}{3} x$	$=$	$\frac{7}{3} - 1$
	↓	Fasse zusammen.
$- \frac{2}{3} x$	$=$	$\frac{4}{3}$	$: (- \frac{2}{3})$
$x$	$=$	$- 2$

$\frac{1}{6} x + \frac{3}{2}$	$=$	$- \frac{2}{3} x + 2$	$+ \frac{2}{3} x - \frac{3}{2}$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$\frac{1}{6} x + \frac{2}{3} x$	$=$	$2 - \frac{3}{2}$
	↓	Fasse zusammen.
$\frac{5}{6} x$	$=$	$\frac{1}{2}$	$: \frac{5}{6}$
$x$	$=$	$\frac{3}{5}$

$\frac{1}{6} x + \frac{3}{2}$	$=$	$2 x - 3$	$- 2 x - \frac{3}{2}$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$\frac{1}{6} x - 2 x$	$=$	$- 3 - \frac{3}{2}$
	↓	Fasse zusammen.
$- \frac{11}{6} x$	$=$	$- \frac{9}{2}$	$: (- \frac{11}{6})$
$x$	$=$	$\frac{9}{2} \cdot \frac{6}{11} = \frac{27}{11}$

$2 x - y$	$=$	$6$	$- 2 x$
$- y$	$=$	$6 - 2 x$	$\cdot (- 1)$
$y$	$=$	$2 x - 6$

$x$	$=$	$\frac{1}{2} (y + 1)$	$\cdot 2$
	↓	Der Bruch auf der rechten Seite fällt weg da $\frac{1}{2} \cdot 2 = 1$ .
$2 x$	$=$	$y + 1$	$- 1$
	↓	Linke und rechte Seite vertauschen.
$y$	$=$	$2 x - 1$

$y$	$=$	$3 (2 x - 1)$
	↓	Die Klammer ausmultiplizieren.
$y$	$=$	$6 x - 3$

$1,8$	$=$	$- 0,5 \cdot 2,4 + 3$
$1,8$	$=$	$- 1,2 + 3$
$1,8$	$=$	$1,8$